浙江洞头地区海岛型岬湾海滩的稳定性分析

张建祺，李尚鲁

(1.华北水利水电大学，郑州 450000； 2.浙江省海洋监测预报中心，杭州 310000)

浙江位于整个我国沿海地区，海岛众多，人口密集。其中，占地面积通常大于500 m2的砂质海岛在中国有3 061个，是目前中国拥有砂质岛屿最多的一个省份。目前，浙江省的海洋资源十分丰富，海岸线总长6 486.24 km，占整个中国的20.3%，居于中国首位[1]。浙江虽然砂质海岛众多，海岸线漫长，但是砂质的海滩资源十分的缺乏。浙江海岛的岬湾海滩资源已然成为浙江海岛旅游业发展的重要基石。岬湾海滩形状包括弧形阴影段、缓弯过渡段和平直切线段[2]。岬湾海滩的不稳定会导致岸线侵蚀，危及公路民居，咸水入侵，生物资源退化等。如何从岸线平面形态和竖向剖面形态三维立体地研究岬湾海滩稳定性，有利于全面统筹岬角海湾的修复和防护，合理规划海岛的建设与开发，推动浙江社会经济的可持续发展。因此，将洞头作为典型研究浙南海岸的稳定性问题迫在眉睫。

国内外学者对于岬湾海滩的研究多从平面形态和剖面演变分析两方面展开。平面形态涉及岬湾海滩稳定的模型包括椭圆形模型[3]、对数螺线型[4]，抛物线型[5]等。Moreno Luis J(1999)认为抛物线模型对岬角海滩的适用性比较好，其因为包括可以很好地描述岬角影响的曲线段和直线段[6]，该模型被国内外专家和学者广泛认可。Klein(2003)利用MEPBAY软件对实际海湾分析，证明了岬湾海滩存在的3种状态：静态平衡、动态平衡和不稳定状态[7]，能较好描绘岬湾海滩的地形地貌。相对稳定的“静态平衡”[8]是岬角海湾稳定性极好的形态。剖面演变分析海滩剖面演变是与短周期地貌动力行为相关的海滩过程，是海滩演变研究不可忽视的方面。国外学者收集了海滩剖面的现场实测数据，并进行分析，逐步完善，不断提出各种海滩平衡剖面模式[9-10]，从理论上规范了海滩平衡剖面。国内对海滩平衡剖面规律的研究开展比较少。陈子燊(2002)应用Dean及Bodge等模式对海滩实测剖面数据进行了拟合，但由于数量和区域限制，还不能完全反映海滩平衡剖面特征[11]，仅利用经验函数方法进行有益的研究工作[12]。

现阶段分析海滩稳定性的研究多从岬湾海滩的平面形态、剖面特征等单方面着手。相比较国外，国内对岬湾海滩研究较少，且研究区域为山东、海南等。将浙江海岛作为主要研究区域的岬角海滩平衡性研究尚且不足。笔者选取东岙海滩和金海岸海滩为主要的研究对象，两海滩规模大小相近，受到人工海岸工程或天然岬角的遮蔽影响，且不受其他河流影响。

1 研究区概况

洞头地处浙江温州，别名“百岛洞头”，其海岸线发达，外控温州湾，内扼瓯江口，是进出温州港的咽喉，又是浙南的天然屏障。洞头是全国14个海岛区(县)之一，拥有大小岛屿302个。洞头区岸线蜿蜓曲折，总长333.45 km。沿岸形成众多的天然港岙海湾，且多以岬湾海滩为主。洞头区侵蚀丘陵地貌分布广泛，约占全区陆地面积的91%。比较成规模的港湾有31处，其中大多为规则半日潮港，由于岸线曲折形成比较大的岬角有21处。近年来，先后获批建设浙江省海岛综合开发和保护试验区、浙江省旅游综合改革试点区，是全省海洋经济开发先行先试的地区。随着近年人类活动频繁，经济和社会发展迅速，人类与海岸带环境的冲突十分严峻。

本研究实地测量温州洞头区两处海滩，分别为东岙海滩、金海岸海滩，见图1。

图1 海滩分布图

2 研究方法

2.1 抛物线模型

采用Hsu和Evans(1989)的一种用于静态平衡状态岬湾海滩的抛物线海湾形状方程[5]。方程形式如下：

(1)

C0=0.070 7-0.004 7β+0.000 349β2-0.000 008 75β3+0.000 000 047 65β4

(2)

C1=0.953 6+0.007 8β-0.000 487 9β2+0.000 018 2β3-0.000 001 281β4

(3)

C2=0.021 4-0.007 8β+0.000 300 4β2-0.000 011 83β3+0.000 000 093 42β4

(4)

式中：参照波倾角β为波峰线与控制线之间的波浪倾角；长度为Rβ的控制线为上岬角控制点与下控制点间的距离；Rn为上岬角控制点到海岸上任意一点的极坐标距离；θn为上岬角控制点到海岸上任意一点的极坐标角度；系数C0，C1，C2是关于β的函数，由27个原型海湾与实验模型数据进行回归分析所得。

见图2。

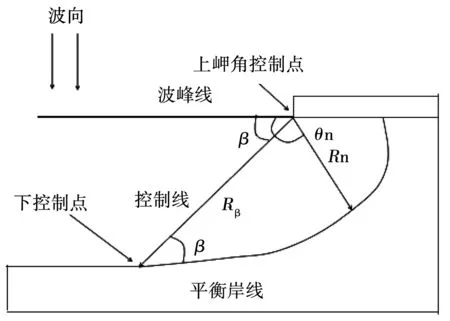
图2 抛物线平面形态模型示意图

2.2 海滩平面形态研究

本文中即采用Klein等开发出的MEPBAY软件对岬湾岸线进行模拟。找到岬角确定上岬角控制点，研究表明静态平衡的岬湾海岸，波峰线基本平行于切线，垂直切线的方向即为盛行波浪入射方向，并且找到以曲线段与直线段连接点为下岬角控制点。模拟海湾的静态平衡岸线，通过与实际岸线的比较可以分析海滩的平衡状态。

2.3 海滩剖面测量

通过2017，2018，2019年3年连续观测，起点为固定于后滨的监测桩，沿着垂直岸线方向向海延伸，测量范围为后滨至低潮线，在地势起伏幅度比较大的区域合理地加密测点；根据海滩长度合理地布设剖面数量，依次展布于整个海滩。其中东岙海滩布设3条、金海岸海滩布设3条。并根据当地潮汐时刻表，于低平潮时刻附近利用RTK人工采集剖面的数据，从而保证剖面数据的完整性。测量时，平面坐标系采用WGS1984大地坐标系，并采用大地高程系统，进而进行数据处理和分析。

3 结果与分析

3.1 海滩平面形态稳定性分析

3.1.1 东岙沙滩

东岙海滩一侧受处人工建筑A所控制，另一侧受到礁石B控制，起到成对岬角的作用。进行分段模拟，首先以点A为上岬角控制点，点C为下控制点，拟合得到静态平衡岸线CD′位于现有岸线CD的海侧；其次以点B为上岬角控制点，点C为下控制点，拟合得到静态平衡岸线CE′位于现有岸线CE的海侧，表明东岙海滩两侧未来有淤积的趋势。见图3。

图3 东岙海滩平衡性模拟

3.1.2 金海岸海滩

金海岸海滩一侧受处岬角A所控制，另一侧受到礁石B控制，起到成对岬角的作用。进行分段模拟，首先以点A为上岬角控制点，点C为下控制点，得到静态平衡岸线CD′与现有岸线CD拟合较好；其次以点B为上岬角控制点，点C为下控制点，得到静态平衡岸线CE′与现有岸线CE拟合较好，表明金海岸海滩处于静态平衡状态。见图4。

图4 金海岸海滩平衡性模拟

3.2 海滩剖面形态稳定性分析

3.2.1 东岙海滩

海滩被堤坝截断，现存海滩长度约为170 m，海滩宽度较窄，约为50～70 m，从北到南一共设置3条监测剖面，剖面S1、剖面S3位于海堤遮蔽区，剖面S2位于较开敞段岸段；坡度变化较为明显，海滩剖面年际稍许变化。整理分析采集的剖面数据，利用surfer软件，绘制海滩三维等高线图、剖面布置图，东岙海滩各剖面对比图以及海滩2017，2018，2019年剖面形态变化图，见图5、图6、图7。

图5 东岙海滩三维等高线图

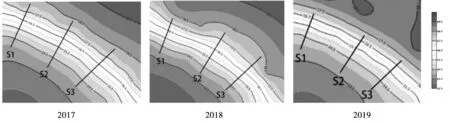
图6 东岙海滩剖面布置图

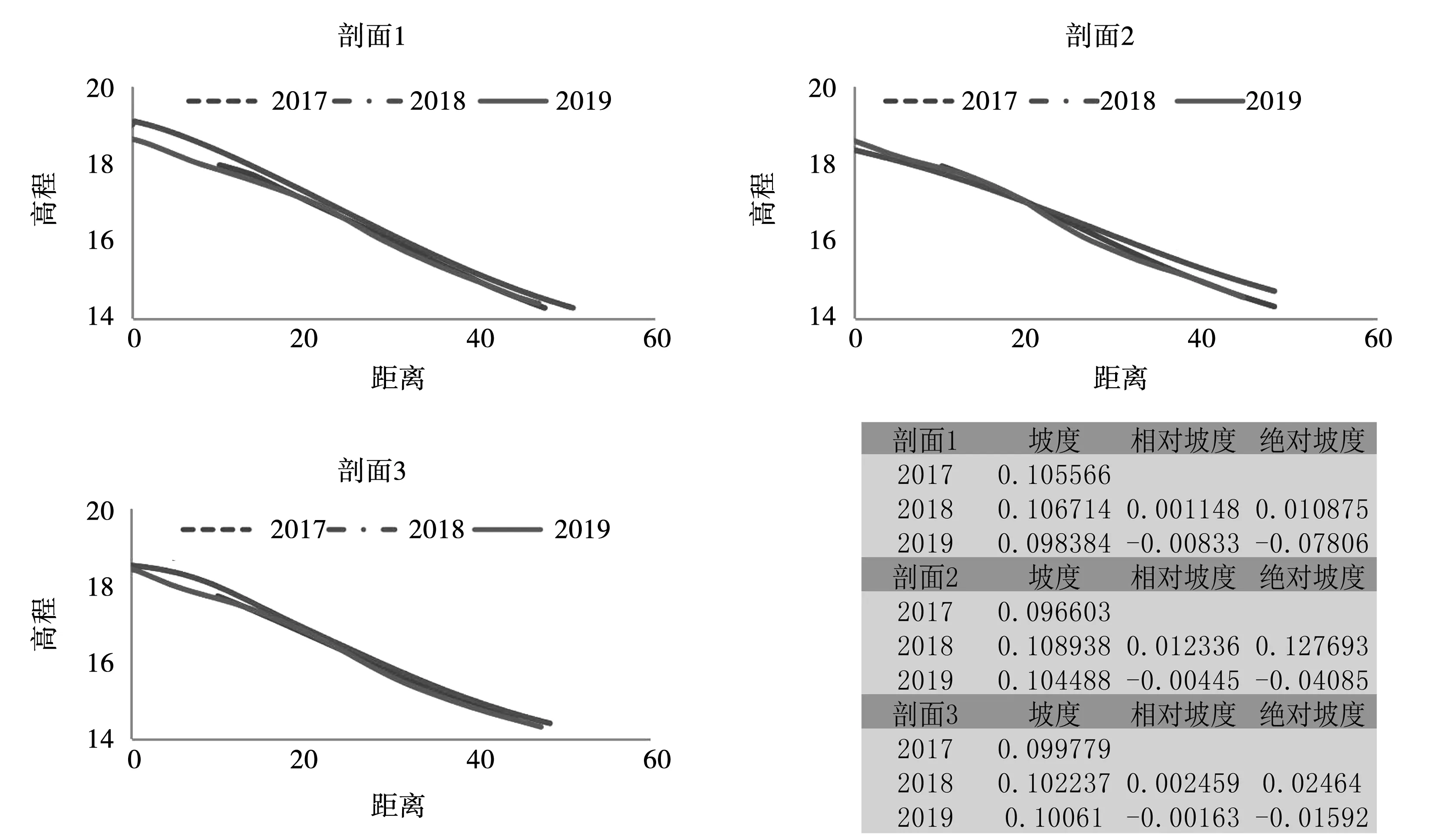
图7 东岙海滩3年剖面形态变化图及坡度变化表

对比3年间的剖面形态差异发现，地形整体发生明显变化，滩面先增高后降低，坡度先变大后变小。对比2017与2019年，海滩略微淤积，但滩面与坡度变化不大，处于动态平衡状态。

3.2.2 金海岸海滩

金海岸海滩两侧发育出天然岬角，海滩长度约为117 m，海滩宽度约为10 m。由南到北布设3条监测剖面，剖面S1位于岬角(礁石)遮蔽区，剖面S2和剖面S3位于较开敞段岸段，整体坡度比较缓，海滩剖面年际变化不太明显。整理分析采集的剖面数据，利用surfer软件，绘制海滩三维等高线图、剖面布置图，金海岸海滩各剖面对比图以及海滩2017，2018，2019年剖面形态变化图见图8、图9、图10。

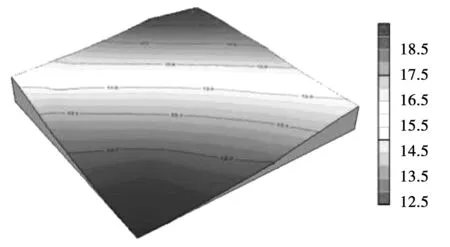
图8 金海岸海滩三维等高线图

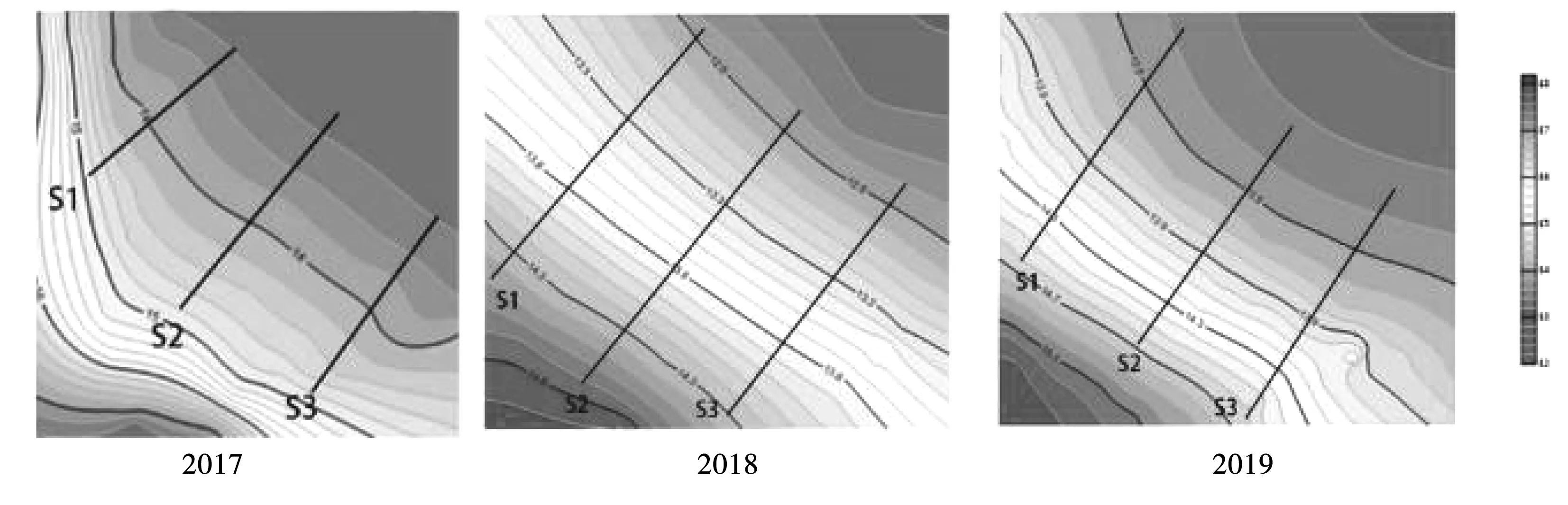
图9 金海岸海滩剖面布置图

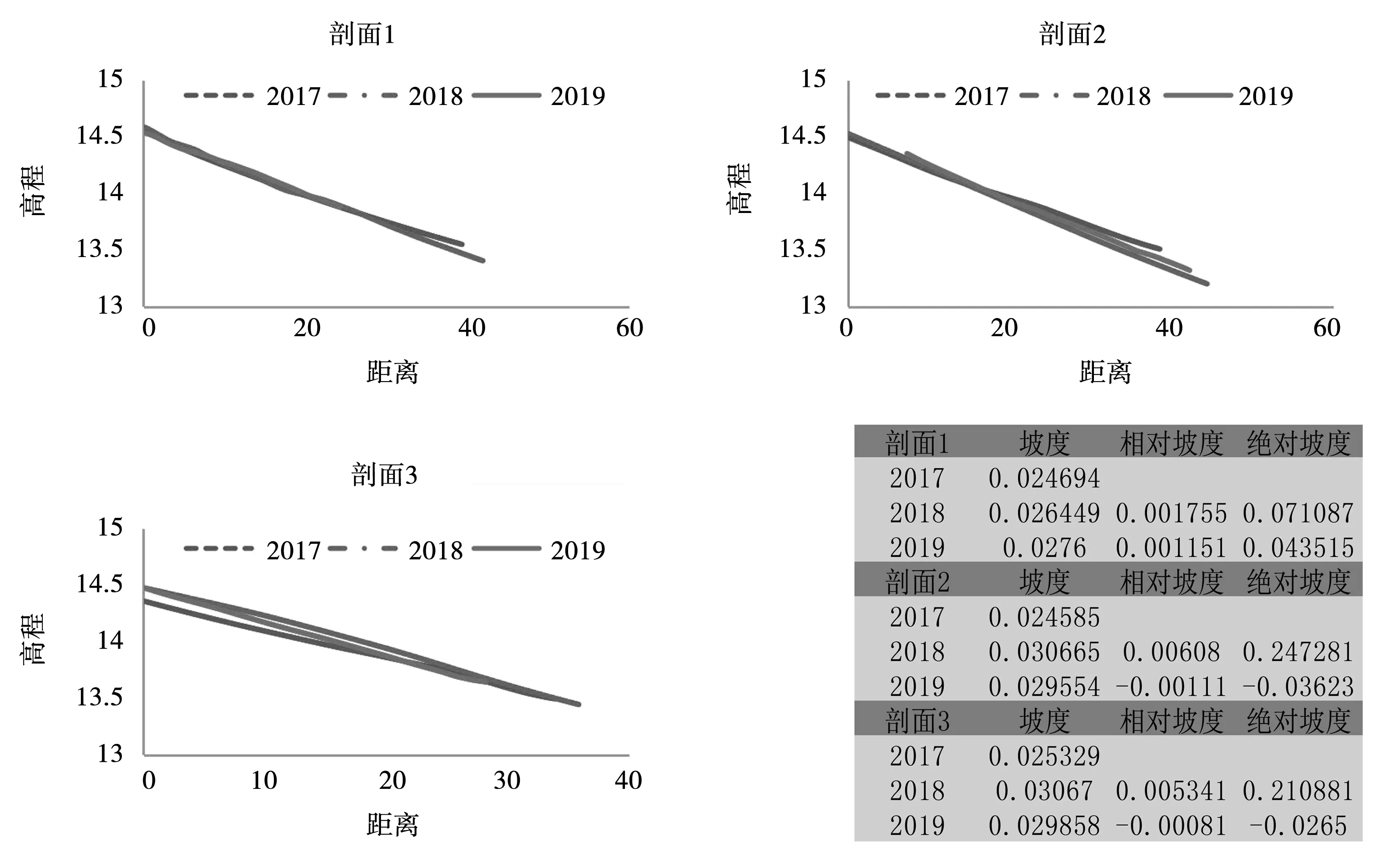
图10 金海岸海滩3年剖面形态变化图及坡度变化表

对比3年间的剖面形态，整体并无发生明显变化，整体坡度较缓，坡度基本没有变化。发现前滨地形发生较少变化，滩面少量加高。

3.2.3 东岙沙滩与金海岸沙滩剖面形态的区别

综合分析看出，东岙海滩整体上前滨地形变化不大，滩肩部分因为铺砂高度少量增加，宽度增大，坡度略微变大，但随着自然演变，高度及坡度慢慢恢复；中间开敞部分前滨部分先淤积再侵蚀，位于堤坝遮蔽区的剖面则出现堆积。由此认为，该海滩处于动态平衡状态。金海岸海滩在自然状态下较为稳定。同时，在观测期内持续侵蚀或淤积的情况很少，存在轻微的淤积和侵蚀的交替变化，整体变化幅度极小，说明海滩相对稳定。

4 结 论

1) 应用抛物线模型模拟了两个海滩的静态平衡岸线，结果表明东岙海滩岸线处于淤积和侵蚀的交替变化的动态平衡状态，在自然动力和人工补滩下，靠近堤坝的岸段将持续堆积，直至达到静态平衡；金海岸海滩岸线拟合结果与真实岸线基本重合，表明海滩基本处于静态平衡状态。

2) 在剖面形态上，东岙海滩整体受人为影响较大，2017-2018年的观测期间，整体上表现为滩面增高，坡度变大；剖面S3前滨因人工铺沙出现陡坎，滩肩以上堆积，滩肩以下侵蚀，但随着一年的人类活动与自然作用下，2019年剖面表现为滩面降低，坡度减小，略有侵蚀。因此，东岙海滩总体较稳定，未来可能有淤积的现象。3年观测期间，金海岸海滩整体滩面几乎保持不变，坡度基本不变，整体上变化幅度较小，海滩处于稳定状态。