浅阱中双组份玻色-爱因斯坦凝聚体基态的稳定性研究
周小燕, 梁青青, 赵春艳
( 兰州文理学院 传媒工程学院, 甘肃 兰州 730070 )
玻色-爱因斯坦凝聚体(Bose -Einstein condensate,BEC)[1]由美国科学家埃里克·康奈尔等于1995年在实验中首次发现.因BEC不仅可为研究量子力学的基本问题提供一个宏观系统,而且还可应用于原子激光、精密测量、量子信息和量子计算等领域,因此受到国内外学者的关注,并取得了大量的研究结果[2-9].近年来,学者们对有限深势阱中单组份BEC的稳定性进行了大量的研究,结果表明影响BEC稳定性的因素有很多,如原子之间的相互作用,囚禁原子数目的多少,凝聚原子与热原子之间的相互作用等[10-11].也有学者对双组份BECs的稳定性进行了研究,结果表明双组份凝聚体的稳定性比单组份BEC的稳定性更加复杂,其稳定性既与同组份原子内部和不同组份原子之间的相互作用有关,还与囚禁的原子数多少有关[12-14].目前,学者从原子的临界数和基态能量方面对BEC的稳定性研究得较少,基于此本文在不考虑相分离和热原子影响的情况下,利用变分法分析有限深势阱中两组份凝聚体的稳定性,得出凝聚体塌缩的临界条件,并从有效势和能量的角度分析凝聚体的稳定性.
1 模型方程
首先给出两组份凝聚体的耦合方程:
(1)
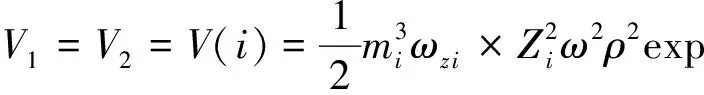
Ψi(x,y,t)=ψi(x,y,t)fi(z,t),
(2)
其中fi(z,t)表示轴向方向的波函数.将轴向波函数fi(z,t)定义为
(3)
其中lz i是描述其中任一组份凝聚体轴向长度的物理量.利用式(2)和(3)可得到二维轴向方向的GPEs方程:
(4)
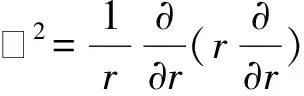
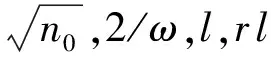
V(r)=r2exp (-cr2).
(5)
由此方程(4)变为:
(6)
2 有限深势阱中两组份凝聚体的基态
本文使用高斯型试探波函数研究凝聚体在V(r)=r2exp (-cr2)中的稳定性.高斯型试探波函数为
(7)
其中Ai和Ri分别是波包的振幅和宽度.波函数(7)满足归一化条件
(8)
1) 从原子数方面来讨论基态的稳定性.方程(6)在柱坐标下的拉格朗日密度为
(9)
将方程(5)和(7)代入方程(9)中,可得到方程(6)的有效拉格朗日方程:
(10)
将方程(5)变为
V(r)=εr2exp (-cr2),
(11)
并将其代入到方程(10)进行重复计算.令R1=R2=R,a1=a2=a, 则根据∂Leff/∂Ai=∂Leff/∂Ri=0和方程(8)可得出N与k,k1,c,R之间的关系式为
(12)
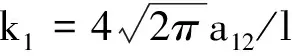
(13)
由式(13)可知,只有在满足k+k1<0的条件下,两组份凝聚态才有可能存在稳定态,即满足a+a1<0的条件下存在稳定态.由以上可知,当给定相互作用系数k和k1时,就可以得出一个临界原子数上限;当原子数超过这个临界值时,系统就会塌缩:这表明组与组的相互作用对凝聚体的稳定性具有重要的作用.
2) 从基态能量方面讨论凝聚体的稳定性.二维凝聚体在有限深势阱中的基态能量为
(14)
将方程(7)代入方程(14),得基态的能量为
(15)
求基态能量的极值后可得基态宽度的方程:
(16)
令R1=R2=R,g1=g2=g,N1=N2=N/2, 则方程(15)和(16)可分别简化为:
(17)
(18)
从方程(18)可知,只有当g+g12> -8π时,方程(17)才有意义,即当体系满足g+g12> -8π时才会有稳态出现.该结论和式(13)一致.

