一类非线性薛定谔方程解的衰减估计
2020-06-01 08:38韩琦悦李春花
延边大学学报(自然科学版) 2020年1期
韩琦悦, 李春花
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
非线性薛定谔方程
在光学领域中具有重要应用[1].方程中v是一个未知的复值函数,v=v(t,x),t≥0,x∈R;p>1;μ(t)是一个实值函数;λ∈C.若λ=-1,μ(t)=a≤0, 则有
(1)
式中t≥0,x∈R,p>1.2009年, M.Ohta等[2]研究了方程(1)的大初值整体解的存在性和不存在性.2016年, Jin等[3]研究了方程
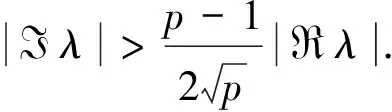
(2)
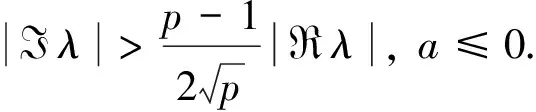
1 预备知识
定义1设m,s为非负实数,定义Sobolev空间为
为了表述方便,本文简记Hm,0(R)=Hm(R).
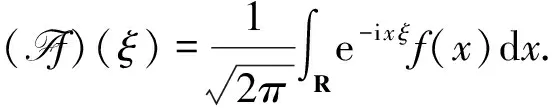
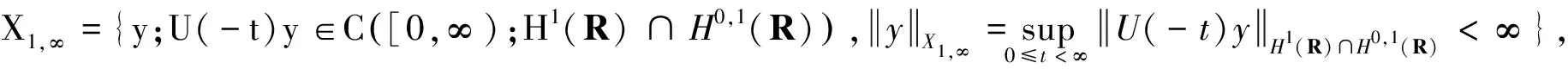
(3)

引理2[4]设u∈X1,∞是方程(3)的整体解,则有:
2 主要结果及其证明
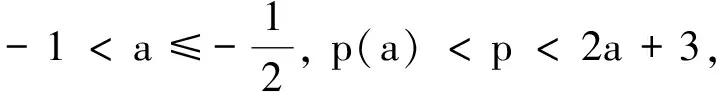
证明在定理1条件下,由文献[4]知方程(2)存在唯一整体解v(t,x)∈X1,∞.下面应用文献[3]的方法证明方程(2)整体解的衰减估计.
(4)
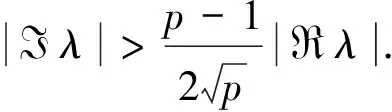
在方程(4)两边同时作用FU(-t), 则有
其中
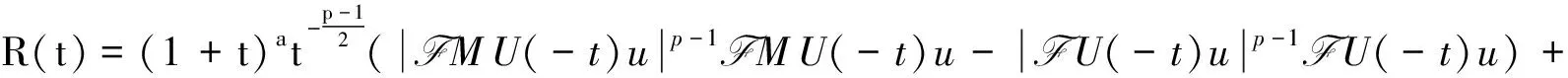
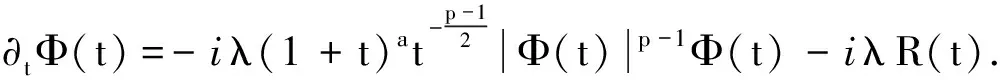
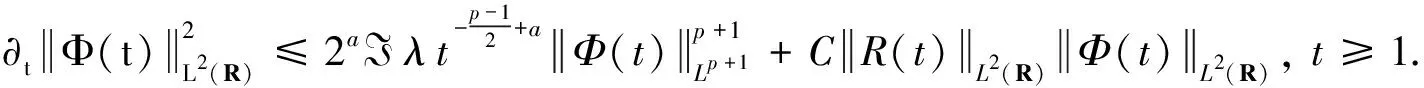
(5)
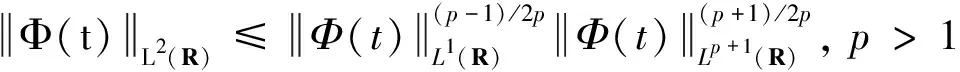
(6)
将式(6)代入式(5),得
(7)
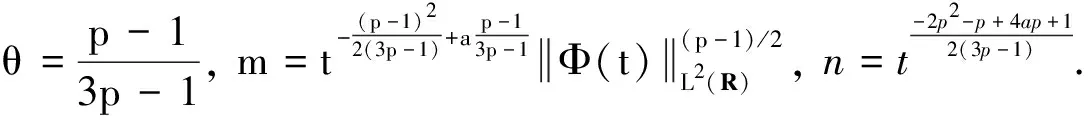
将上式代入式(7),则存在η>0使得
(8)
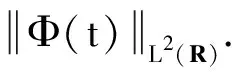
(9)
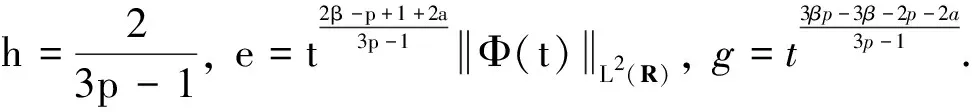
将上式代入式(9)得
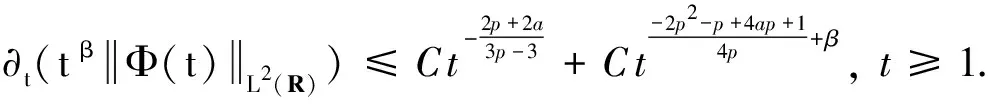
(10)
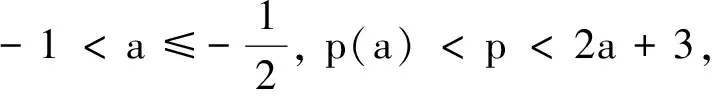
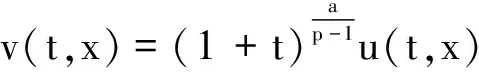
猜你喜欢
数学物理学报(2022年5期)2022-10-09
数学物理学报(2022年1期)2022-03-16
数学物理学报(2021年6期)2021-12-21
流行色(2019年7期)2019-09-27
初中生世界·七年级(2019年8期)2019-08-29
中国航海(2019年2期)2019-07-24
幽默大师(2019年6期)2019-01-14
神州·下旬刊(2017年6期)2017-10-28
中央民族大学学报(自然科学版)(2016年1期)2016-06-27
中国卫生(2015年7期)2015-11-08

