非扩张映射隐中点黏性迭代序列的逼近问题和均衡问题

沈金良， 叶静妮， 黄建华

(1.福州大学 至诚学院， 福建 福州 350002; 2.福州大学 数学与计算机科学学院， 福建 福州 350108 )

0 引言

近年来，许多学者对非扩张映射的不动点问题和均衡问题进行了研究，并取得了较好的研究结果[1-5].对于二元函数G∶C×C→R， 其均衡问题(简写为EP)可定义为：寻找x∈C， 使得

G(x,y)≥0 (∀y∈C).

(1)

将式(1)的解集记为EP(G)，EP(G)={x∈C:G(x,y)≥0,∀y∈C}.

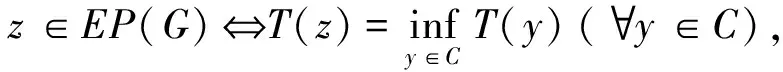
2009年， Ceng等[5]在Hilbert空间中研究了k-集伪压缩映射T的迭代序列：

(2)

并在适当的条件下证明了序列{xn}和{un}弱收敛于T的不动点集和均衡问题解集的公共点.2014年，Alghamdi等[6]在Hilbert空间中提出了一种非扩张映射半隐中点迭代序列：

(3)

其中{αn}⊂(0,1)，T∶H→H是非扩张映射，并且在合适的条件下得到了该序列的弱收敛定理.2015年，Xu等[7]在Hilbert空间中利用黏性逼近方法构造了一种非扩张映射隐中点迭代序列：

(4)

其中{αn}⊂(0,1)，f是压缩映射，T是非扩张映射,并在某些条件下得到了该序列的强收敛定理.2019年，沈金良[8]研究了如下非扩张映射T的隐中点迭代序列：给定x1∈C，

(5)

其中{αn}⊂(0,1)， {rn}⊂(0,∞)， 并且在Hilbert空间中得到了该序列的弱收敛和强收敛定理.

受以上研究启发，本文定义如下非扩张映射的隐中点黏性迭代序列：给定x1∈C，

(6)

其中f是压缩映射，T是非扩张映射，不动点集记为F(T).本文在Hilbert空间中研究式(6)的均衡问题和不动点问题，并且在适当的条件下证明序列{xn}和{un}强收敛于F(T)∩EP(G)中的某一个点z，z=PF(T)∩EP(G)f(z).

1 预备知识

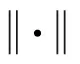
称PC为H在C上的投影算子，则显然PC是非扩张映射，且对于x∈H以及z∈C有

z=PC(x)⟺〈x-z,z-y〉≥0,∀y∈C.

为了求解均衡问题EP(G)， 本文假设G满足以下4个条件：

(A1)G(x,x)=0,∀x∈C;

(A2)G是单调的，即G(x,y)+G(y,x)≤0,∀x,y∈C；

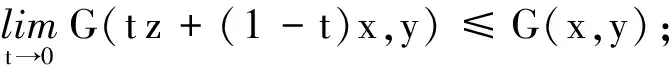
(A4) 对任意的x∈C,yG(x,y)是凸的和下半连续的.

定义1设C是H的闭子集，T∶C→C，f∶C→C是两个自映射，则：

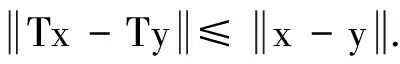
2)T在零点是半闭的，若对于C中的序列{xn}，xn⇀x0∈H和Txn→0可以推导出Tx0=0.

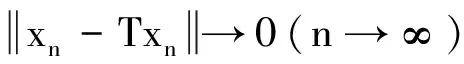
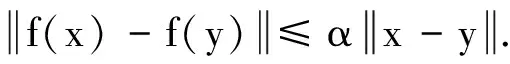
引理1[9]设H是实的Hilbert空间，则下列等式成立：

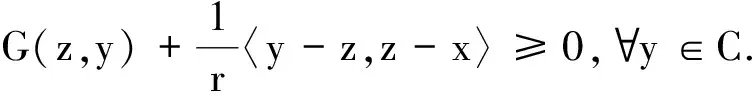
(1)Sr是单值的；

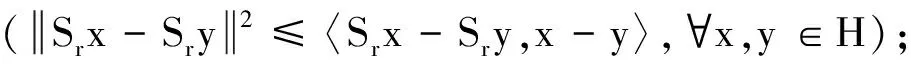
(3)G(Sr)=EP(G);

(4)EP(G)是非空闭凸的．

引理4[11]设C是H的非空闭凸子集，T∶C→C是非扩张映射.若T有不动点，则I-T在0点是半闭的(这里I是H中的恒等映射)，即如果C中的任意序列{xn}弱收敛于x∈C，且有序列{(I-T)xn}强收敛到y， 则有(I-T)x=y．

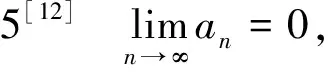
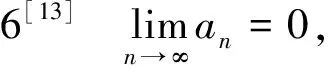
2 主要结果及其证明

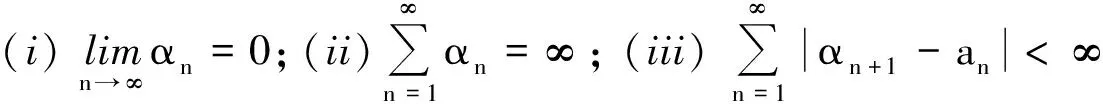
证明1)任取q∈Ω， 由引理3中Sr的定义可知un=Srnxn， 因此

(7)

因为T是非扩张映射，所以

(8)

根据式(7)和式(8)进行移项整理得

再由递推公式可知

(9)

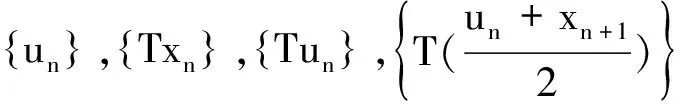
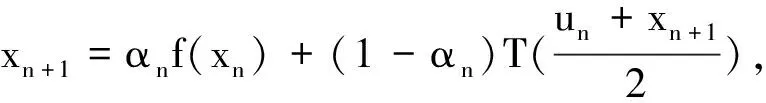
(10)

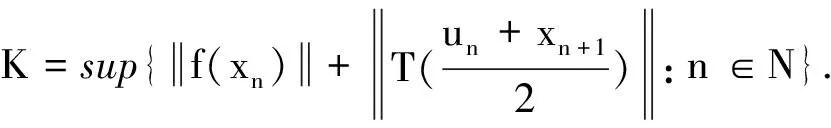
由式(6)可得：

(11)

(12)

在式(11)中取y=un +1， 则有

(13)

在式(12)中取y=un， 则有

(14)

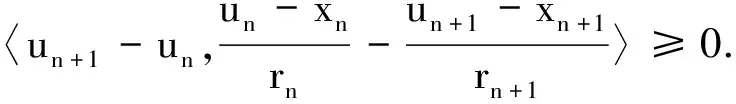
(15)

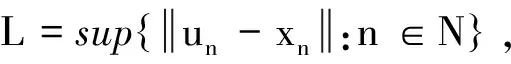
(16)

由式(10)和式(16)可得

对上式进行移项整理得

由条件(ii)、(iii)、(v)以及引理5可推导出

(17)

(18)

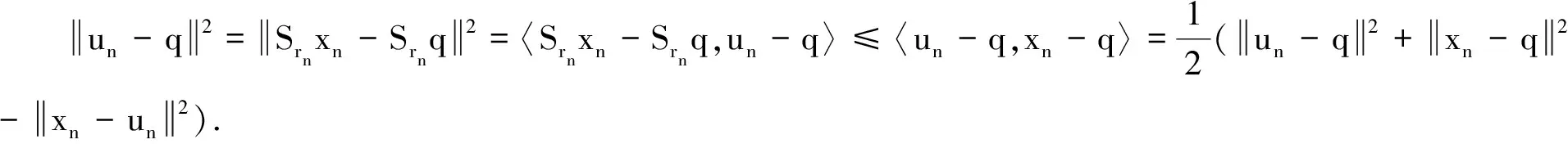
(19)

由引理1中的(ii)和式(19)有

对上式进行移项整理得

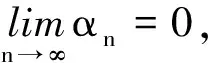
(20)

由引理1的条件(i)和式(17)、(18)可得

(21)

由式(17)、(20)和式(21)得

(22)

再由式(20)和(22)得

(23)

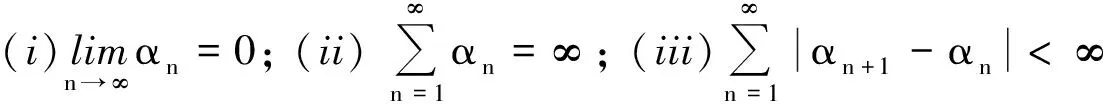
证明分两步证明定理2.

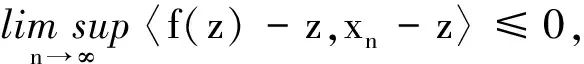
(24)

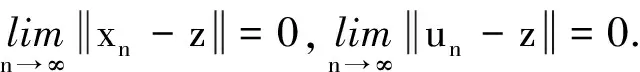
由范数和內积的性质可知

因此,

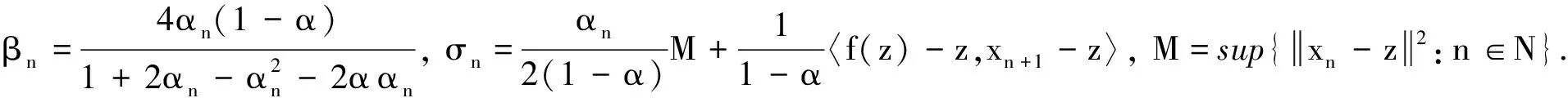
(25)

(26)

由上述过程可知，序列{xn}和{un}强收敛于z∈Ω， 同时z也是变分不等式〈(I-f)y,x-y〉≥0,x∈Ω的唯一解，即z=PΩf(z).