半明半暗公路隧道运营期偏压状态研究
王福和,王树新
(中交第一航务工程局有限公司,天津 300461)
0 引言
随着我国工程建设环保意识的加强,洞口地表偏斜段采用半明半暗结构形式是符合“早进晚出”、“洞口少开挖”、“绿色进洞”的隧道洞口位置确定原则的[1]。半明半暗进洞方案能够有效平衡山体推力,最大程度地减少山体扰动,较好地适应偏压地形,保证隧道进洞安全,满足环境保护和水土保持的要求[2]。半明半暗洞口段地质条件复杂,影响因素较多,荷载多变,而且其本身结构复杂,设计施工难度很大,主要体现在[3]:1)半明半暗段围岩节理、裂隙发育,岩体破碎,稳定性差,大多处于偏压位置;2)当受到施工扰动或雨水影响后,围岩的物理力学性质易发生较大变化;3)半明半暗法施工需要更多工序,结构受力转化频繁。在施工过程中,稍有不慎,易产生大变形,严重时甚至出现裂缝[4]。
偏压隧道形成的原因主要分为两种,一种是施工造成的,另外一种是地形地势等客观原因导致的。施工造成的偏压大多是临时性的,施工过后即可降低偏压状态。但由于地形地势等客观原因导致的偏压,施工期的风险比较大,为了降低施工期间半明半暗段偏压隧道的风险,以往的研究偏重于施工方法[5]和开挖方法[6-8]的研究。目前很多地方的高速公路项目都是政府和社会资本合作形式,即PPP 项目,施工单位还要参与运营期的道路管理。偏压隧道作为道路安全控制性节点,其运营期的安全性是非常重要的。一般隧道施工期都是非雨季施工,尤其半明半暗的洞口段,而运营期间遇到雨季则是不可避免的,陈伟等[9]研究了降雨时,若偏压隧道不排水则受力增加;若偏压隧道排水较好,则受力基本不变,但并没有讨论其偏压比是否变化。运营期超过20 a 的隧道,尤其是西南地区,大概率的面临地震的侵袭,在此状况下,半明半暗隧道的偏压状况也应引起重视。为此本文开展运营期间半明半暗偏压隧道的安全性研究。
1 有限元模型
1.1 模型尺寸
数值模拟计算隧道采用二维模型,底部取80 m宽,坡顶高度采用44 m,坡底高度采用26 m,土层分为2 层,强风化花岗岩和中风化花岗岩,强风化花岗岩厚度约5 m。隧道衬砌厚度0.9 m,挡墙高度12.5 m,挡墙顶部宽度1 m,底部宽度4 m。挡墙和山体之间在施工隧道成拱以后回填拌和碎石。整体采用四边形网格,并且在隧道衬砌周围的网格尺寸约为0.3 m,四周网格宽度为1 m,整个模型网格数量为9 873 个,见图1。

图1 模型尺寸Fig.1 Model size
1.2 计算参数
本模型中强风化花岗岩、中风化花岗岩和拌和碎石采用摩尔库伦模型;隧道衬砌、挡墙采用弹性模型。其中隧道衬砌以C30 混凝土为主,挡墙采用C20 混凝土浇筑,拌和碎石采用C15 混凝土作为拌料。具体参数取值如表1 所示。
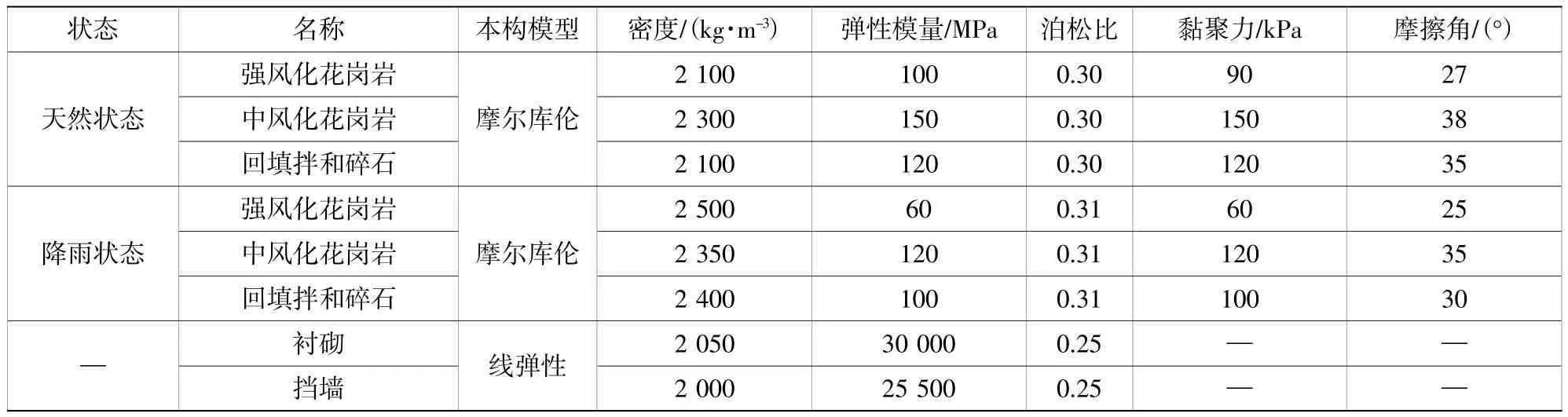
表1 计算参数Table 1 Calculation parameters
1.3 计算工况
本模型不考虑开挖工法对结构应力分步的影响,两种工况分别为:
工况1:降雨。降雨不考虑渗流对边坡的影响,只考虑其密度和强度参数的变化。故首先采用表1 中的参数在重力作用下得到整个模型的地应力场。随后更换参数如表1 所示,计算得到降雨条件下的地应力场。整个模型受重力作用;为了避免边界条件对地应力场分部的影响,底部边界水平和竖向同时固定约束,两侧采用水平方向约束,竖向不约束。衬砌、挡墙、回填拌和碎石和土体两两接触之间采用绑定约束。
工况2:地震。隧址所在区域的地震动峰值加速度为0.10g,对应地震烈度为7 度。按照设计要求,隧道提高一级设防按8 度设防。整个模型受重力作用;地震荷载作用下,左右两侧和底部设为无反射边界;地震波加在底部水平方向。
2 无反射边界理论
由于计算机容量有限,一般只能在有界区域上计算,为此需引进人工边界,在这些边界上应加相应的边界条件。这些边界条件应满足两个基本要求[10]:1)新的有界区域上的解应是原来的无界区域上解的近似。对波动方程来说,这就要求在人工边界上不产生人工(非物理)反射。因而这类边界条件称为无反射边界条件或吸收边界条件;2)所形成的微分方程初边值问题是适定的。
在有限元中,无反射边界主要有:黏性边界条件,无限元边界条件[10]。黏性边界条件[11-12]为在半无限介质边界上设置具有一定阻尼系数的阻尼,阻尼则成为吸收应力波的器件。黏性边界条件设置有两种方法,一种是直接在相互作用的特殊设置中添加阻尼,另一种是在相互作用的连接菜单中设置阻尼。黏性边界适用范围最广,能适用于散射问题,但是需设置阻尼参数,应力波吸收效果不太显著[13]。无限元边界是在模型边界上设置无限单元[14]。无限单元是为了克服有限单元在求解无界域问题时的不足而提出的,常用的无限元有Astley 映射共轭无限元和Burnett 无限元[15],如图2 所示的二维无限单元。

图2 二维无限单元及其要素Fig.2 Two-dimensional infinite element and its elements
Ⅰ、Ⅱ、Ⅲ、Ⅳ这4 个结点是构成该无限元几何形状的最基本要素:Ⅰ、Ⅱ间的连线是无限单元的边界;Ⅰ~Ⅲ和Ⅱ~Ⅳ是无限单元的边,分别趋于无限远处;Ⅰ、Ⅱ两点称为无限单元的角结点,Ⅲ、Ⅳ称为无限单元对应边的中结点。无限单元在几何上比较简单,它的两条边在笛卡儿坐标系中始终保持为直线,这就是说,用Ⅰ~Ⅲ和Ⅱ~Ⅳ两条直边已足够描述无限单元的几何特征。无限单元通过它的边与相邻的无限单元或趋于无限的边界相连,通过它的边界反映近场信息,或与近场的有限单元相连。
无限单元与有限单元的一个重大区别是前者具有方向性,即Ⅰ、Ⅱ、Ⅲ、Ⅳ这4 个结点在局部坐标系中的顺序是固定的。无限单元在几何上的一个重要特点是两条边在趋于无穷的方向上不能相交,在数学上就是要求无限单元在无限方向上必须是发散的,只有这样,才能保证物理量在趋于无限过程中的一致单调性。对所生成的无限单元,必须逐个检查以保证符合该条件。
3 计算结果及分析
3.1 原始地层计算结果
如图3 所示,在原始地应力作用下隧道处于偏压状态,最大应力位置点位于浅埋侧的挡墙和隧道拱交界附近,与马杲宇等[16]结果一致。

图3 原始地层状态隧道受力图(Pa)Fig.3 Tunnel stress diagram in original stratum state(Pa)
图4 和图5 展示了原始地层作用下,隧道的位移和弯矩图。说明该处隧道受地形影响,导致隧道偏压,其位移和弯矩最大值都位于深埋侧拱肩处和浅埋侧的拱脚底部。

图4 原始地层状态隧道位移图(m)Fig.4 Tunnel displacement diagram of original stratum state(m)

图5 原始地层状态隧道弯矩图(N·m)Fig.5 Tunnel bending moment diagram in original stratum state(Nom)
3.2 降雨对偏压隧道的影响
计算结果表明,降雨作用下,隧道受力有所增加,最大应力值从6.385 MPa 增加到9.152 MPa,最大应力点都位于浅埋侧的拱脚附近;隧道位移略有增加,最大位移点都位于深埋侧的拱肩处,整体位移规律没有变化;隧道弯矩略有增加,最大弯矩点都位于深埋侧的拱肩处和浅埋侧的拱脚底部。
3.3 地震对偏压隧道的影响
地震作用下,隧道受力有所增加,最大应力值从6.385 MPa 增加到9.44 MPa,最大应力点都位于浅埋侧的拱脚附近;隧道位移略有增加,最大位移点都位于深埋侧的拱肩处,但地震作用下,隧道发生整体下沉;隧道弯矩略有增加,最大弯矩点都位于深埋侧的拱肩处和浅埋侧的拱脚底部。
3.4 结果分析
如图6 所示,隧道以中轴线为界,左侧为深埋侧,右侧为浅埋侧。共提取12 个点的应力、位移和弯矩,其中 1-1'、2-2'、3-3'、4-4'、5-5'和6-6'关于隧道中轴线对称。图6 右侧坐标系包含2个坐标系,左侧横轴表示弯矩比,纵轴对应隧道的取值点;右侧横轴表示位移和应力比,纵轴对应隧道的取值点。6-6'处的弯矩比是负值,表示浅埋侧值比深埋侧的小;反之,表示浅埋侧值比深埋侧的大,例如1-1'处的原始位移比是正值,表示1-1'处的位移浅埋侧的值比埋深侧的大。

图6 隧道偏压状态对比Fig.6 Comparison of tunnel bias state
由图6 中的弯矩比可知,原始地应力作用下,在拱肩靠上的6-6'处的弯矩比较大;降水或地震作用下,在同一位置处6-6'弯矩比有所降低。位移比和应力比在降雨和地震作用下变化较大。地震作用下,隧道两侧的位移比都是负值,即深埋侧的位移较大,浅埋侧的位移较小。降水条件下,在拱脚2-2'处的位移比比原始状态下有所降低。
4 结语
本文针对已建设成的偏压隧道运营期的偏压情况进行了研究。在降雨和地震作用下,隧道衬砌结构的位移和荷载以及弯矩都有所增加。但其偏压状态并不一直增加,比如在降雨作用下,其深埋侧和浅埋侧的弯矩比并没有增加,而是比正常状态下小,地震工况下也是相同结果。总体来说,降雨和地震作用下,偏压隧道的偏压状态并没有恶化。在实际运营监测中,需依据不同的控制指标对隧道不同部位进行监控量测,现实情况下弯矩难以监测,一般监测位移和应力。降雨条件下,应加强拱肩顶部的位移监测;地震条件下,隧道不同断面可能发生整体位移,可能发生不同断面的剪切破坏,应加强轴向位移监测。

