管线渗漏引发地面塌陷的DEM-CFD耦合数值模拟
张小玲,王晓丽, 杜修力,许成顺
(北京工业大学 城市与工程安全减灾教育部重点实验室, 北京 100124)
近几年城市地下管线因破损渗漏诱发地面塌陷的现象层出不穷,给国家带来了巨大的财产损失[1]。城市地陷具有突发性、随机性、隐蔽性等特点,当这种地面塌陷发生在人群密集区时,更会造成极大的经济损失同时也对居民的生命造成威胁,因此研究地下管线渗漏诱发地面塌陷的灾变机理具有十分重要的现实意义。
地下管线渗漏诱发地面塌陷的问题,从微观角度分析是土体在水流作用下的流失问题和地面土体逐渐失稳塌陷的机理和过程,重点是流体与土颗粒的相互耦合问题[2]。从本质上讲,岩土材料都是由离散的、尺寸不一、形状各异的颗粒或块体组成,因此在该问题的研究上将土体视为离散单元更合理。目前针对渗流问题的研究计算效率较高的方法是土体采用离散单元法(DEM),流体采用计算流体动力学方法(CFD),将两者结合起来考虑耦合作用时采用DEM-CFD计算方法。
目前,许多学者针对管线渗漏引发地面塌陷事故的外因与内因进行了研究。在外因方面,主要研究管线渗漏水压、渗漏范围、管线位置等因素对地面塌陷的影响。张成平等[3]通过室内试验发现地表沉降值和沉降范围会随着管线渗漏水范围的增加而增大,而管线位置与管内水压通过影响渗漏范围间接影响地面塌陷程度。陶高梁等[4]通过其研制的渗流破坏模型试验装置, 分析了泄漏孔径和泄漏水压力对砂土渗流破坏的影响规律,发现泄漏孔径越小,产生空洞的临界水压力越大。在内因方面,主要研究土体颗粒级配、孔隙率或土颗粒与流体间的相互作用力等因素的影响。Vincens等[5]通过考虑接触力的分布、接触数和平均应力来分析土壤颗粒的内部稳定性。 Scholtes等[6]在恒定围压条件下进行了三轴试验,发现土体发生渗透破坏后土体的剪胀性和峰值应力减小。
随着离散元软件的推广,计算方法的不断完善,应用DEM或DEM-CFD耦合计算方法研究渗流微观问题得到推广。Ma等[7]采用DEM-CFD计算方法分析了水力梯度与流速的关系,分析了孔隙率,粒径组合和颗粒间滚动阻力对流动特性的影响。还有一些学者修改了经典的DEM-CFD计算方法以使流体网格更精细化或计算方法更准确。蒋明镜等[8]基于流体的可压缩性修改了经典DEM-CFD计算方法,通过单颗粒自由沉降速度符合理论解验证改正方法的可行性。王胤等[9]考虑颗粒的形状效应对DEM-CFD计算方法的影响,总结了颗粒滚动阻力对沙堆休止角与土体堆积孔隙率的影响。
目前在应用DEM-CFD耦合计算方法进行流体与土颗粒相互作用的研究主要是针对流体流速较小符合达西定律时的缓慢流动。这种情况下,由于流体压力分布不均而作用于单位质量土体上的力(本文称之为流体压力梯度力) 影响很小可忽略不计,但当流体不满足达西定律的高速渗流或者土颗粒尺寸较大、形状不规则时,流体压力梯度力的影响不容忽略。刘先珊等[10]通过土颗粒的运动位移间接反应了流体压力梯度力的存在,而目前的大部分研究未考虑流体高速渗流时流体压力梯度力对流固耦合过程的影响。
本文主要基于DEM-CFD双向耦合计算方法,考虑高速渗流时流体压力梯度力对流固耦合作用的影响,重点从机理角度分析流体渗流过程中土体力学特性和流体水力特性的变化规律与动态变化过程。
1 CFD-DEM 流固耦合原理
目前关于研究流固相互耦合作用的问题主要包括流体和流体之间的相互作用、土颗粒和流体的相互作用和土颗粒与土颗粒的相互作用。
1.1 流体与流体的相互作用
1.1.1 连续性方程
连续性方程指的是流体在运动过程中满足质量守恒定律,即单位时间内通过体积元的质量净通量等于体积元内质量的变化量。具体的表达式[11]如式(1)所示:
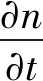
(1)
式中:n为土体孔隙率,v为流速矢量。
1.1.2 动量方程
Navier-Stokes方程是描述黏性不可压缩流体动量守恒的运动方程,即单位时间内单元体动量的增加必等于单位时间净流入单元体的动量加上单元体内流体所受合力。在流体流动过程中,不可压缩流体动量增加来源有:黏性力产生的动量,压差力产生的动量,体积力产生的动量和颗粒对流体作用力产生的动量。一般黏性不可压缩流体Navier-Stokes方程表达式为:
(2)
式中:v是流速矢量;ρf为流体密度;g为重力加速度;p为流体压力;τ为流体的黏性应力张量;fint为单位体积内颗粒与流体的作用力。
1.2 土颗粒与流体的相互作用
渗流过程中土颗粒与流体的相互作用力包括流体对颗粒的拖曳力,流体压力梯度力,浮力,粒子运动引起的滞流阻力以及其他不稳定力等。为简化计算,在流固耦合计算过程中只考虑拖曳力、流体压力梯度力和浮力。
ffluid=fdrag+fgrad+ffloat
(3)
式中:ffluid是指流体对颗粒的作用力;fdrag是指流体对颗粒的拖曳力;fgrad是流体压力梯度力;ffloat是颗粒在流体中的浮力。
以下针对渗流过程中流体对颗粒的作用力中的拖曳力、流体压力梯度力和土颗粒所受浮力具体进行计算推导。
1.2.1 拖曳力求解
目前对于流体施加给土颗粒的拖曳力的计算,即便是形状规则的土颗粒组成的多孔介质,也没有明确的计算公式,主要是通过试验数据拟合多孔介质的拖曳力,本文应用的计算公式[12]为:
(4)
式中:Cd为拖曳力系数;d为颗粒直径;u为颗粒速度矢量;v是流速矢量;n为颗粒所在流体单元的孔隙率,经验系数χ计算公式为:
(5)
拖曳力系数Cd计算公式为:
(6)
式中:Re为雷诺数,计算公式为:
(7)
式中:μf为流体动力黏滞系数。
1.2.2 流体压力梯度力求解
在渗流过程中流体压力梯度力计算公式:
(8)
当流体满足达西定律时:
(9)
式中:uxo是流体的平均流速;k是土体的渗透系数。
当流速较大不满足达西定律且土体孔隙率≤0.8时,流体压力梯度▽p采用Ergun[13]公式:
(10)
当渗流过程中土体孔隙率大于0.8时,流体压力梯度▽p采用Wen等[14]的计算公式:

(11)
1.2.3 浮力求解
渗流过程中土颗粒所受浮力的计算公式:
(12)
1.3 土颗粒与土颗粒的相互作用
基于牛顿第二定律,土颗粒所受的作用力包括土颗粒所受外力、流体对土颗粒的作用力、土颗粒自身重力,计算公式如下:
(13)
(14)
2 DEM-CFD耦合过程
2.1 耦合过程
由于CFD模块无法模拟真实流体在土体中的流动状态,因而基于体积平均原理[15]将流体划分为若干个粗网格,每个粗网格代表一个流体单元,以流体单元内流体的平均特性来代表该单元的特性,该单元内的流体信息平均分配给单元内的土颗粒,相邻流体单元通过信息传递来体现流体的流动性。本文在计算过程中考虑了非稳定流时流体压力梯度力对流固耦合过程的影响,具体的DEM-CFD流固耦合计算流程见图1。
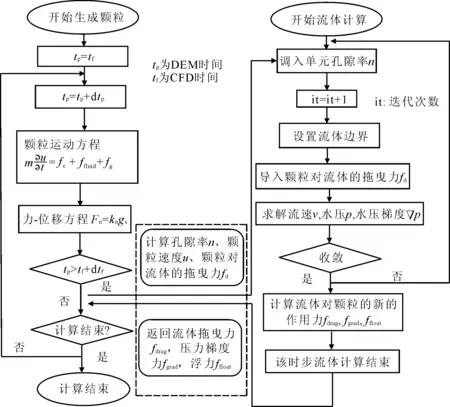
图1 CFD-PFC流固耦合流程图
图1左侧为采用离散元软件PFC3D建立的力学模型流程图,右侧为利用CFD模块建立的流体模型流程图,中间区域为DEM-CFD交互模块。DEM与CFD模块的耦合计算以两者计算时间是否相等为判断条件。首先DEM模块将土体孔隙率n、颗粒的速度u、颗粒对流体的拖曳力fd等信息传递给CFD模块, CFD模块根据传入信息求解流速v、水压p、压力梯度▽p等信息;若CFD模块通过计算判断流体N-S方程收敛,则将流体对颗粒的拖曳力、流体压力梯度力、浮力传递到DEM模块。若N-S方程不收敛,则根据流体边界条件重新计算流速v、水压p、压力梯度▽p等信息再进行收敛判断。在耦合过程中为了保证计算的稳定性,在CFD模块设定流体100时步内为稳定,DEM模块每20时步更新颗粒的作用力,拖曳力,孔隙率等参数。
2.2 模型尺寸验证
目前针对管线渗漏引发地面塌陷问题的研究,多数成果都是针对二维模型进行了计算[16],这与实际工程情况存在一定差异。本文采用离散元软件PFC3D建立了管线渗漏引发地面塌陷的三维数值模型进行计算。考虑到计算效率与适用性,因计算模型尺寸与土颗粒尺寸不能同时满足实际的要求,在建立三维计算模型时以土颗粒尺寸和颗粒数量为参考依据,土颗粒粒径采用实际粒径,生成的颗粒数量与二维计算模型颗粒生成数量接近。
为了考察三维计算模型尺寸对计算结果的影响,本文建立了不同尺寸大小的渗流计算模型,通过分析流体压力梯度力的计算结果来确定最终的模型尺寸。图2是在渗流深度相同(均为20 cm)的情况下,渗流入水口面积分别为15 cm×15 cm,20 cm×20 cm,30 cm×30 cm和40 cm×40 cm四种条件下流体压力梯度力的对比结果。从图2可以看出,当入水口面积为20 cm×20 cm,30 cm×30 cm和40 cm×40 cm时,流体压力梯度力的峰值与最终的稳定值都比较接近;但是当入水口面积为15 cm×15 cm的数值结果与其他结果相差较大。图3比较了当流体压力梯度力趋于稳定时不同模型计算的总时间,由图可以看出,所建立的模型尺寸越大,计算的颗粒数量就越多,所需的计算时间越长。因此综合考虑各因素,本文采用20 cm×20 cm的模型尺寸来进行下一步的数值计算。
3 计算结果分析
由于离散元软件无法反映流体在土体孔隙中的真实流动过程,因此在所建立的模型上游施加非零水压p,下游水压为0,上下游存在初始压力梯度▽p,在该压力梯度的作用下通过相邻流体单元的信息传递来模拟流动过程。本文考虑的是管线破损后渗漏水对周围土体的侵蚀作用,通过用土体上下游两端的压力梯度▽p代替水流从管线中渗漏而出的水压力。图4为渗流过程的模型示意图。其中上游入水口为y=0的x-z平面,大小20 cm×20 cm,下游出水口为y=20 cm的x-z平面,大小20 cm×20 cm ,其他边界为不透水边界,水流以一定流速v从上游垂直流入。
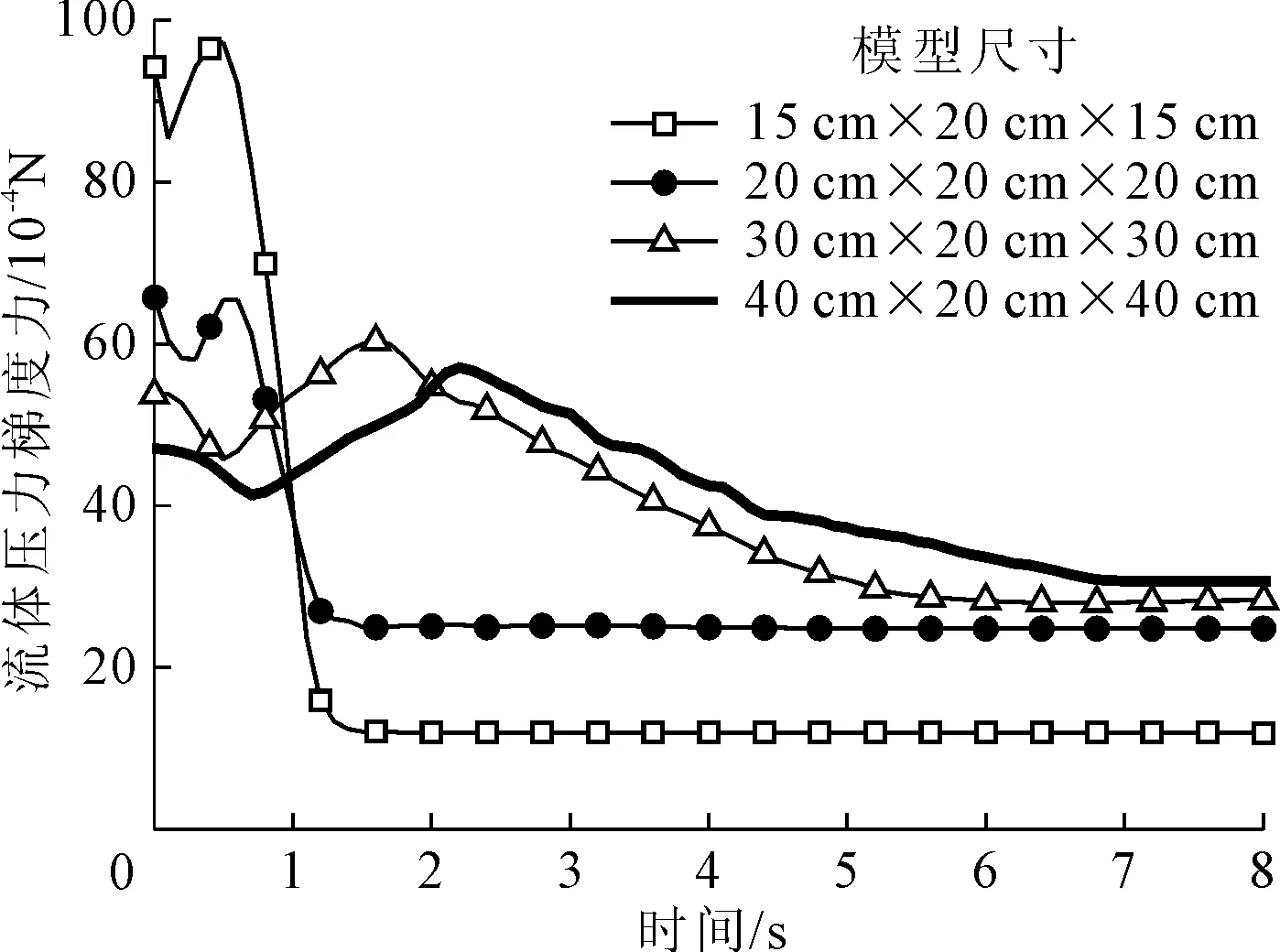
图2 模型尺寸影响

图3 不同模型计算总时间对比

图4 渗流过程模型示意图
地表突然发生大规模塌陷,则土体内部已产生容纳上方土体的空间[17],因渗流过程产生的大尺寸裂隙或实际土体内已存在的土洞、早期人防工程等均可容纳上方土体,因此本文在建模过程中考虑了地下空洞的存在,模拟自然界天然形成的空洞,空洞周围没有衬砌。在生成土颗粒力学模型时,考虑计算效率与颗粒数量的合理性,取计算模型大小20 cm×20 cm×20 cm,土颗粒粒径4 mm,土颗粒数量大约11.6万个,土体的中间位置存在半径为5 cm的球形空洞,管线与空洞的位置与大小详情见图4(b)。计算模型采用的土颗粒计算参数见表1,流体与墙体计算参数见表2。流体网格划分单元为1 cm×1 cm×1 cm,共有20×20×20个网格。根据杨斌等[18]关于多孔介质渗流规律的描述,流体从线性层流过渡到非线性层流临界流速为0.002 3 m/s~0.007 8 m/s,从层流转化为紊流的临界流速为0.016 m/s~0.048 m/s。因此本文在分析流体压力梯度力的作用时,对比了满足达西定律的流速与不满足达西定律的流速流体压力梯度力的变化规律,其中满足达西定律的流速为0.001 m/s,不满足达西定律的流速为0.1 m/s、0.2 m/s、0.3 m/s。

表1 土颗粒计算参数

表2 流体与墙体计算参数
3.1 空洞上方土体失稳坍塌过程
图5(a)—图5(e)是沿渗流方向某截面的土颗粒在流体压力梯度▽p作用下逐渐失稳直至坍塌的演化过程示意图。
由图5(a)可看出,在流体渗流过程中,空洞上方土颗粒最先失稳发生运动,随着渗流过程的进行,土体失稳范围越来越大,并逐渐向地表扩展。当土体失稳范围延伸至地表时,地面开始出现轻微凹陷,此时空洞上方土体均产生微小位移,见图5(b),空洞几何形状发生变化。随着土体压力梯度的改变,空洞上方土颗粒在自重与流体渗流力等共同作用下,继续向下运动且位移逐渐增大,塌陷范围进一步向地表拓展,该失稳过程经过多次循环后,地表松动颗粒范围越来越大,地表沉降凹槽深度也越来越大。由图5对塌陷过程的模拟结果可知,土体塌陷过程中产生了倾斜的滑移面,模型表面呈现近似圆锥形的破坏形态。本文所用土颗粒粒径为4 mm,隶属于土的工程分类标准[19]中的粗粒土,这跟已有研究[17]中认为的粗粒土地层地陷形状近似为圆形漏斗状的结论基本一致。
半连续和连续模型的影响。在使用两种模型类型的默认参数的第一个评估周期中,本文发现连续声学模型比半连续声学模型在开发集上的效率为36.10%。

图5 土体坍塌过程位移变化 (单位:cm)
3.2 流体水力性质变化规律
土颗粒在渗流过程中受到的流体压力梯度力与流压梯度▽p有关,因此在流体速度为0.1 m/s,0.2 m/s,0.3 m/s三种工况下,分析了地表与A点土体两端水压差值▽p1的变化。图6反映了该水压差值▽p1随渗流时间变化规律,由图6可以看出,▽p1随渗流时间呈现先减小后趋于稳定的变化规律,而稳定渗流的结果是在渗流过程中上下游的水头差不随时间变化,由此可知本文模拟的地下管线渗漏引发地面塌陷的过程是非稳定渗流过程。
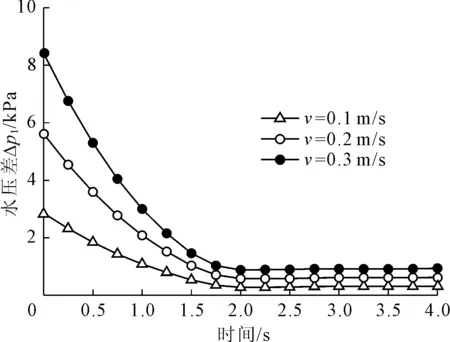
图6 土体上游与A点两端水压差随时间的变化
3.3 土颗粒力学性质变化规律
本文研究管线渗漏后引发地面塌陷的机理以空洞上方土体的变化为主要研究对象,计算了空洞上方距离地表0.04 m处的一个流体单元(图4中A点)内的土颗粒在流体作用下拖曳力fdrag、浮力ffloat、流体压力梯度力fgrad的变化情况,由于分析流体对颗粒的作用力时流体单元较小,因此作用力数值较小,计算结果分别见图7、图8。
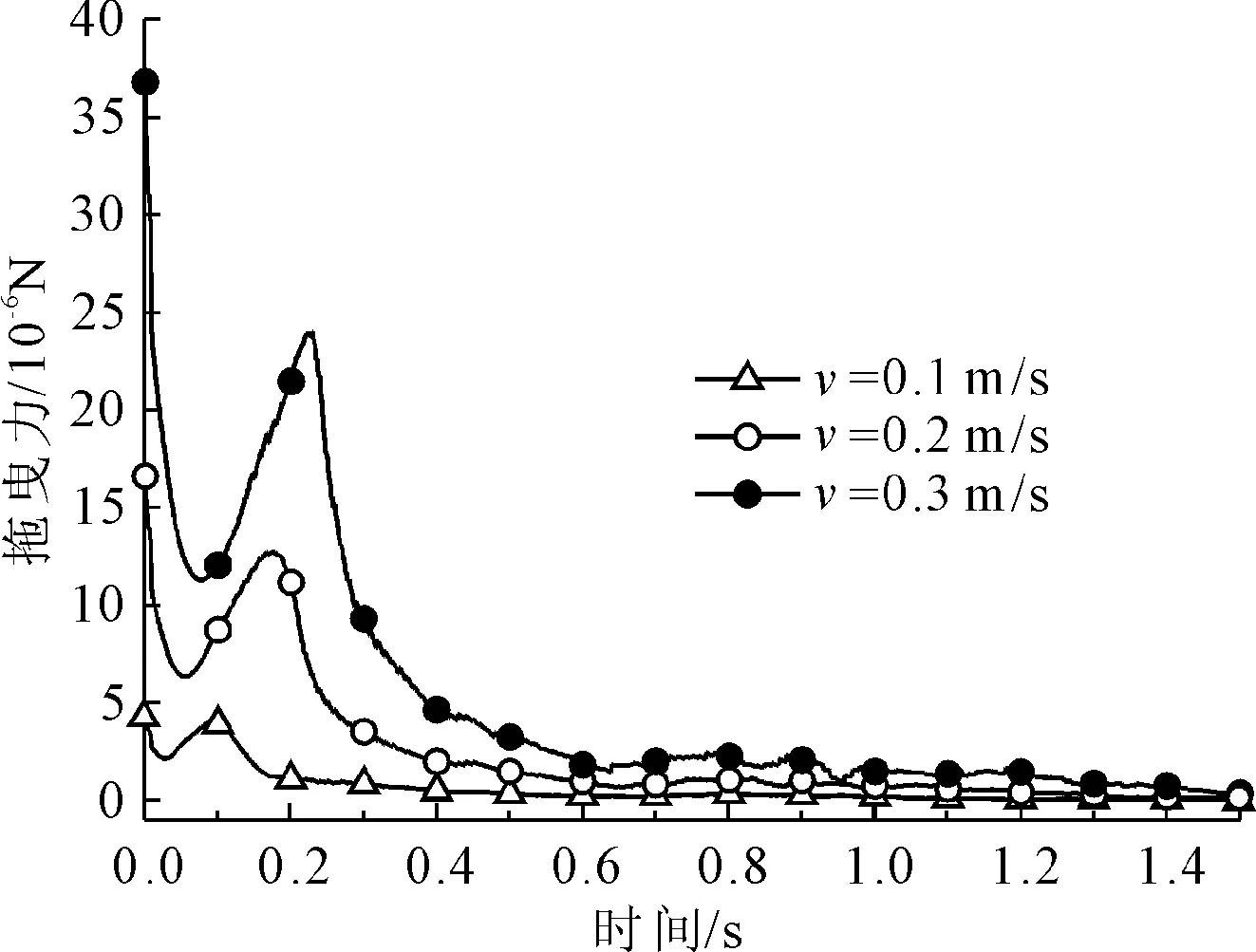
图7 流体对土颗粒的拖曳力

图8 土颗粒所受压力梯度力
图7是计算一个流体单元内所有颗粒受到的平均拖曳力fdrag随时间变化曲线。在整个计算过程中当流速为0.1 m/s,0.2 m/s,0.3 m/s三种工况下土颗粒受到的流体拖曳力由最大值急剧减小后增大再减小趋于稳定。这是因为拖曳力的大小取决于颗粒与流体运动的相对速度,见公式(4)。在流体发生渗流过程的初始阶段,由于土体刚接触流体作用力,流体运动速度与土颗粒的运动速度差值最大,此时土颗粒受到的流体拖曳力在整个计算过程中为最大值。随着图6流体压力梯度▽p1的减小,颗粒与流体的相对速度减小,土颗粒受到流体的拖曳力随即减小。当运动的土颗粒从空洞上方的土体中流失掉落至空洞,此时流体与土颗粒的相对速度又急剧增大,因而土颗粒受到的拖曳力又急剧增大。当空洞下侧土体与下游土体水压差超过某值时,土颗粒重新发生流失过程,颗粒所受流体拖曳力开始缓慢减小。与蒋明镜等[8]的研究中单个颗粒最终沉降速度为0.321 m/s时的拖曳力为8×10-6N相比,本文计算的拖曳力结果与蒋明镜等[8]研究中的拖曳力结果相当,但由于本文研究的流体单元内含有多个土颗粒,因此图7拖曳力结果数值会偏大。
当流体流速为0.1 m/s,0.2 m/s,0.3 m/s三种工况时,在渗流过程中土颗粒受到的浮力计算结果相同,具体数值大约为3.28×10-4N。
图8是渗流过程中土颗粒受到的流体压力梯度力随时间变化曲线。由图可看出,在整个渗流计算过程中,当流速为0.1 m/s,0.2 m/s,0.3 m/s时,土颗粒受到的流体压力梯度力由最大值急剧减小,后又增大最终缓慢减小趋于某稳定值,由公式(8)—式(10)可知,流体压力梯度力与流压梯度▽p有关,而▽p又与颗粒与流体运动的相对速度有关,因此流体压力梯度力变化原因与土颗粒受到的拖曳力原因类似。但当流速为0.001 m/s,流体压力梯度力数值几乎接近于0 N,说明流体满足达西定律时不需要考虑流体压力梯度力的影响;但流体高速渗流时,流体压力梯度力与浮力数量级相同,且其数值大于拖曳力,因此在求解流体对土颗粒的作用力方程时不能忽略流体压力梯度力的影响。
由于土颗粒的尺寸与几何形状影响流体压力梯度力,因此针对土颗粒半径为2 mm、3 mm、4 mm时的流体压力梯度力进行了计算对比,结果如图9所示。由图可以看出,在计算时间内不同土颗粒半径时的流体压力梯度力的变化规律基本相同,但土颗粒半径越大,流体压力梯度力越大,最终趋于稳定的时间越快。
在渗流过程中对比流体压力梯度力、拖曳力和浮力的计算结果可知,图8中流速为0.001 m/s时流体渗流满足达西定律,土颗粒所受的流体压力梯度力数值很小,可以忽略不计;但当流速为0.1 m/s,0.2 m/s,0.3 m/s时,土颗粒所受流体压力梯度力与浮力数量级相当,且在数值上要大于拖曳力,因此在求解力学方程中其数值不容忽视。在针对地下管线渗漏引起地面塌陷问题的研究中,很多学者都仅考虑了土颗粒所受流体拖曳力和浮力的影响而忽略了流体压力梯度力的影响,这会导致极大的误差。因此本文在分析高速渗流引发地面塌陷的问题时,考虑了流体压力梯度力对土体颗粒力学性能的影响。

图9 不同土颗粒半径的流体压力梯度力随时间的变化
3.4 渗流过程中土颗粒流失规律
通过试验手段分析土体渗流过程,只能从宏观角度观察到土体的侵蚀形状,土体内部具体流失细节难以直接观察,采用数值模拟的方法可以反映土体流失过程中的颗粒流失详情、土体力链演化规律与土体内部颗粒的重组过程。在地下管线发生渗漏后,只有当土体内部流体的水力梯度高于起始水力梯度[20],流体克服了结合水的粘滞阻力时,土体内部的流体才会发生渗流。在流体压力梯度▽p作用下土体中的流体发生渗流的过程中,描述颗粒流失现象的参数有土颗粒流失速率、土颗粒接触数变化量、土体孔隙率等指标。图10、图11、图12分别对渗流过程中这些参数的变化规律进行了计算分析。
土颗粒流失速率是指某时间段内土颗粒流失数量占上一时间段颗粒数量的比重。图10是施加了压力梯度▽p后流体发生渗流的过程中,土颗粒的流失速率随时间的变化曲线图。图中的点代表本文数值模拟得到的土颗粒流失速率结果,曲线为对土颗粒流失速率进行拟合得到的曲线。由图中的结果可知,在流速为0.1 m/s,0.2 m/s和0.3 m/s三种工况下,在整个计算时间内土颗粒流失速率均大于零,且为一种波动式增长,说明在流体渗流过程中土颗粒一直处于流失状态。在前期流失阶段,颗粒流失速率成比例增加,到后期颗粒流失速率急剧增大,这是因为在渗流过程中土体内部流体对土颗粒的渗透力需要一定的时间维持。前期土颗粒排列紧密,颗粒流失过程较缓慢;随着土颗粒的流失,土体内部形成贯通的渗流通道并不断扩大,更多的土颗粒发生流失,流失现象更加明显。随着压力梯度越大,即流体的流速越大,土颗粒的流失越快。
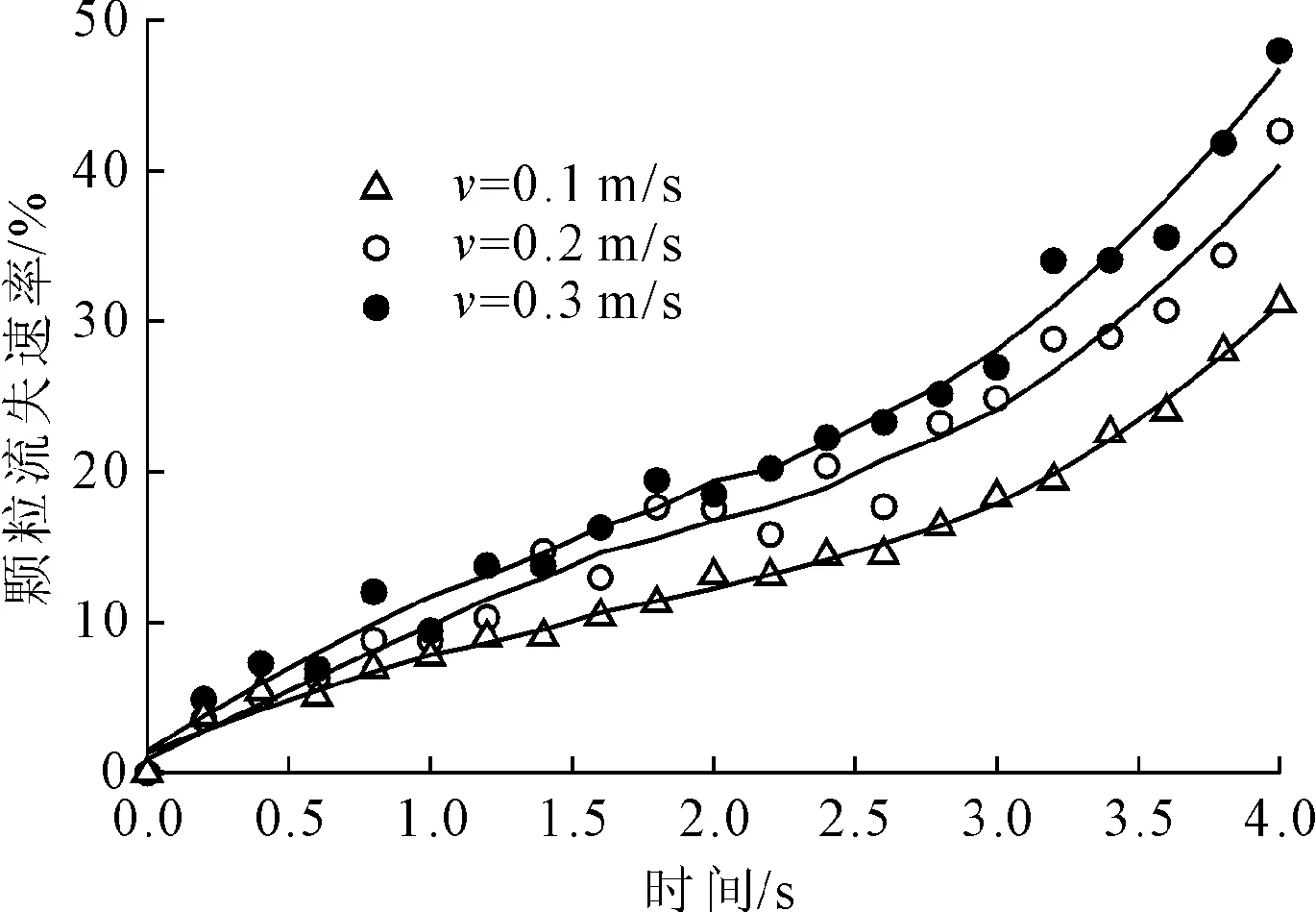
图10 土颗粒流失速率随时间的变化

图11 土颗粒接触数变化量随时间变化

图12 土体孔隙率随时间的变化
土颗粒的接触数是指渗流发生的过程中,某一时刻土体内部颗粒之间接触粘结部位的总数量,接触数变化量是指该时刻土体内部的接触数与上一时刻接触数的差值。接触数变化量能够反映短期内土体内部颗粒之间在流体压力梯度▽p作用下的碰撞激烈程度与粘结状态。图11是在渗漏水不同的流速下的土颗粒接触数变化量的变化趋势。由图可以看出,在流体流速v=0.1 m/s,0.2 m/s和0.3 m/s时,土颗粒接触数的变化量均呈现先减小后增大的变化趋势。若土颗粒的接触数变化量大于零,说明此时间段内土体在水流作用下内部土颗粒接触数量越来越多,颗粒粘结位置增加,土体密实度增大;若土颗粒的接触数变化量小于零,说明土颗粒间的粘结数量减小,此时间段内土颗粒正处于流失状态。同时,由图可以看出,该数值模型中大约0.4 s时刻是颗粒流失量正负值的突变时刻,说明该时刻是土体内部接触力链减小和颗粒间开始出现松动的临界时刻;而0.8 s时刻是接触数变化量变化趋势的转折点,说明此时刻土颗粒的流失速率达到最大。土颗粒接触数变化量的曲线斜率后期缓慢减小到0,体现了土颗粒在水压差的作用下土体流失速率由快到慢最终趋于稳定的变化规律。
土体孔隙率也是衡量土颗粒流失程度的重要指标之一。图12所示为土体上下游两端在流体压力梯度▽p的作用下位于空洞上方土体孔隙率随时间的变化情况。由于渗流过程中孔隙率计算区域土体位于空洞上方,该区域土颗粒流失迅速,因而计算时间相对较短。由图可以看出,土体孔隙率前期变化较缓后迅速增加到1,这是因为前期土颗粒排列紧密,当土体上下游两端存在流体压力梯度时,土颗粒开始缓慢流失。随着渗流过程的进行,土体内部孔隙逐渐形成贯穿通道,土颗粒流失速率加快,当孔隙率计算区域的土颗粒全部流失后,土体孔隙率即达到1。
4 结 论
(1) 本文对经典的CFD-DEM 耦合计算方法做进一步的改进,在高速渗流过程中引入了流体压力梯度力对流固耦合过程的影响。流体压力梯度力在高速渗流流速较大时,流体压力梯度力与浮力的数量级相当其数值大于拖曳力,且土颗粒半径越大,流体压力梯度力越大。
(2) 在渗流过程中土颗粒流失速率在整个计算过程中缓慢增加;土颗粒接触数变化量呈现先减小后增大的变化趋势;土体孔隙率先缓慢增加后迅速增大。
(3) 地下管线渗漏引发地面塌陷的过程中,空洞上方的土颗粒最先失稳发生运动,松动的颗粒逐渐向地表延伸,土体内部产生倾斜滑移面,地表最终呈现圆锥形凹陷,整个塌陷过程中的塌陷模式呈圆锥形变化。

