重力坝坝基多斜面抗滑稳定模糊体系可靠度研究

钱 龙，王 刚，李梦瑶，李向鹏

(大连理工大学 水利工程学院， 辽宁 大连 116024)

对于混凝土重力坝，坝基深层抗滑稳定研究是其结构安全可靠性分析的重要一环[1]。重力坝坝基岩体失稳可能包含多种失稳通道(或路径)，而将具有多失稳通道的基岩视为体系可靠度模型中的串并联系统将更加符合工程实际[2]。同时，工程实践和理论分析表明，决定重力坝坝基稳定可靠性的几何与物理力学参数、失稳准则中的安全系数允许值等往往存在多种不确定性，它们的取值边界通常并不十分清晰，即存在一定程度的模糊性。抗滑稳定计算参数的随机性、模糊性以及失效准则的模糊性是重力坝抗滑稳定模糊体系可靠度分析中要考虑的问题[3-4]，也是当前大坝安全与可靠性研究中的难点问题之一。因此，将体系可靠度与模糊理论结合，对随机与模糊不确定因素组合下重力坝的抗滑失稳问题进行研究，是完善重力坝设计理论的重要基础性理论工作，也是保障重力坝安全稳定运行的重要技术手段。

目前在结构体系可靠度研究方面，主要有宽窄界限法[5]、主次结合法[6-7]等；在岩土工程模糊可靠度研究领域，主要是选用合理的隶属函数分别对岩土稳定参数和失效准则(极限状态方程)进行模糊化[8]，通过考虑不同隶属度，得到数个可靠指标的模糊区间，并通过加权平均法来对这些区间进行处理[9]。本文将模糊理论与体系可靠度方法相结合，综合考虑重力坝抗滑稳定参数及失稳准则的随机模糊性，从而进一步深入研究多斜面、多滑移通道复杂重力坝坝基抗滑失稳评价理论，虽然本文研究成果是基于某一重力坝工程实例，但研究方法和研究思路仍具有普遍意义上的科研与应用价值。

1 重力坝抗滑稳定模糊可靠度

1.1 随机变量的模糊截集处理

工程实际表明，岩土强度参数(变量)可以用有界正态隶属函数表示其模糊性[10]，模糊隶属函数大多服从数值为正值的近似正态分布，即：

(1)

式中：mx、σx为岩土样本平均值和标准差的估计值；k为隶属函数的取值参数，在边坡工程一般取0.5～3.0[11]。本文主要讨论影响重力坝可靠度的两个重要因素，抗剪断摩擦系数f′和黏聚力c′[12]。

1.2 失效准则界限模糊的隶属函数

模糊理论假定稳定状态到失稳状态之间存在模糊区间，反映到失效准则上，即是安全系数容许值不确定，可将极限状态方程变为[13]：

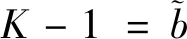
(2)

(3)

式中：λ为隶属度；α是极限状态的最大容差值，其取值主要参照以往工程经验，边坡工程中可取α∈[0.01,0.10]。

1.3 考虑模糊失效概率界限比的模糊可靠度

利用水平截集法可以将模糊极限状态方程变为经典极限状态方程，求解可靠度β的区间值。若要得到一个确定性的值，可取多个隶属度λ，将得到的多个失效概率区间的上下界值通过加权平均得到模糊随机可靠指标，但前提是失效概率区间的上、下界差距不宜过大。边坡工程中一般取λ∈[0.75,1.00]，当λ<0.75时，失效概率计算结果将过于分散从而导致没有实际意义上的参考价值。

目前关于式(1)和式(3)中隶属函数参数k和α取值的研究成果较少。事实上，由于大坝工程的失效概率相对较小，研究工程模糊体系可靠度时，隶属函数的不同形式、隶属函数中参数k和α的取值、隶属度λ的取值，都会导致结果出现较大的差异，为了得到更具有确定性的研究结论，本文提出模糊失效概率界限比的概念。

以R模糊失效概率上下界比值，即

(4)

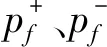
对于某一失效事件，当失效准则隶属函数的隶属度λ一定时，R的变化能代表随机变量的模糊区间范围的大小，R=1时，即不考虑变量的模糊性，而当R>1时，R值越大，变量模糊区间范围越大。

如果工程中存在n个相互独立的失效事件，具均有模糊性，其中以Ri表示因素i(本文指随机变量和失效准则的模糊)对R的影响，对于所有事件则有：

(5)

根据前文定义，若Ri=1，即不考虑因素i的模糊性影响。

对于具有两个模糊因素的问题，用比值Rij=Ri/Rj来代表两者在整体模糊随机失稳事件中所占的比重，可知Rij范围为[1/R,R]，数值越大因素i的模糊性占的比重越高，其上、下界分别代表失稳概率的模糊性完全由因素i决定和完全由因素j决定。

通过规定Ri的值，可以得到对应因素i模糊隶属函数中参数如k或α的具体取值，并进行工程模糊可靠度分析研究，从而得到关于不同因素模糊性占比、隶属函数形式以及隶属函数中参数选定等的定量分析结论，从而保证当调整模糊隶属函数参数k和α时也能将考虑失效准则模糊性的加权平均法用于重力坝抗滑稳定模糊可靠度计算。

2 重力坝抗滑稳定体系可靠度

为便于描述，我们规定，当重力坝基岩中存在多条滑移通道时，将每条滑移通道分别视为坝基抗滑稳定可靠度计算时的一种失效模式，当不同滑移通道之间具有共用滑移面时，各失效模式之间将具有一定的相关性，这时，多条滑移通道可作为可靠度计算的串并联体系考虑。

2.1 体系可靠度的计算

(1) Ditlevsen窄界限法。主要考虑两两失效模式间的联合分布的概率，利用概率论得到体系可靠度界限公式，其形式如下：

(6)

式中：Pfi是事件Ei的失效概率；P(Ei∩Ej)是第i和第j这两个失效模式同时失效的概率，其计算参考文献[11]。

Ei和Ej之间的相关系数ρEiEj，可以通过下式求得：

(7)

式中：αik、αjk是第i、j个失效模式xk中随机变量的灵敏度系数，使用验算点法求得，对于无法求偏导的复杂功能函数，可借助智能优化算法求解[14]。

(2) 主次结合法。结构体系的失效通常是由少数几个主要失效模式引起的，只考虑主、次失效模式的相关性，对Ditlevsen窄界限公式简化得到模型如下：

(8)

式中：Rs是结构可靠概率；ρ12是主次事件的相关系数；式(8)中R0.6计算见下式：

(9)

(3) 蒙特卡洛法。蒙特卡洛法通过对示性函数进行变更来解决体系可靠度问题，若存在m个失效模式的串联体系，将示性函数变为：

(10)

式中：I[gi(x)]表示第i个失效模式的示性函数，多个gi(x)之间应存在共用随机变量的情况，这代表了失效模式间的相关性。

2.2 考虑模糊性的体系可靠度计算

若结构体系的基本结构形式不发生变化，则其整体失效程度会随着其中任一模式失效程度的变化而变化，在重力坝抗滑稳定可靠度分析中，单个滑移通道的模糊可靠度上、下限值对应着模糊体系可靠度的上、下限值。

3 工程算例

3.1 工程概况

某已建重力坝，其坝顶高程为2 564.00 m，最大坝高119.00 m，正常蓄水位和下游水位分别为2 560.00 m和2 471.61 m，淤沙高度52.7 m，取渗透扬压力系数为0.25，某一典型河床坝段的岩基内存在较多的缓倾角软弱结构面。存在五个潜在滑移面，E-F、F-G、G-B、D-F、G-C，这些滑移面共组成四条滑移通道，分别为DFGB、DFGC、EFGB、EFGC。该大坝工程抗滑稳定目标可靠指标值为3.7。本文仅考察基岩内结构面抗剪断参数的不确定性。抗滑稳定可靠度计算时，使用正常蓄水位条件下的荷载组合，即需要考虑大坝和岩体的自重、上下游水压力、扬压力、浪压力、淤沙压力等作用的组合，且均为定值。

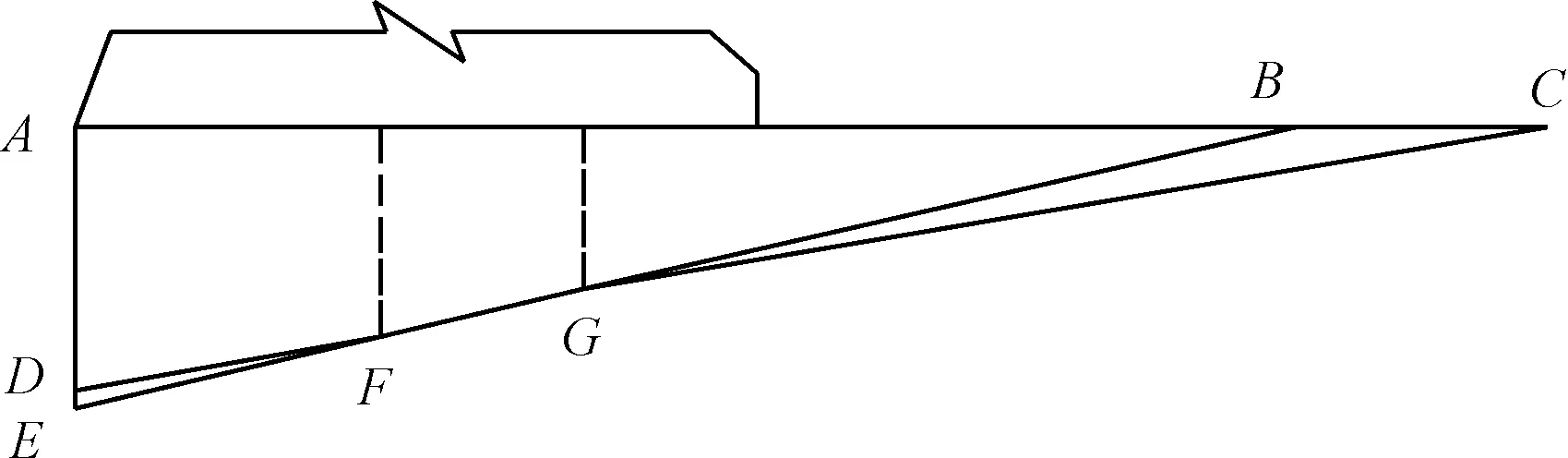
图1 滑移通道示意图

根据现场实测统计资料和已有文献对抗剪断强度参数统计特征的规定，基岩内各滑移面上抗剪断摩擦系数f′和黏聚力c′取值和概率分布特征如表1所示。

3.2 体系可靠度计算

根据文献[15]，使用刚体极限平衡法构建多斜面情况下的极限状态方程，由于安全系数K的计算需要求解非线性方程组，对应可靠度计算的功能函数为非线性隐式功能函数。在本文作者之前研究工作的基础上，可使用差分进化算法[16]求解单个滑移通道的可靠指标和对应的验算点，为便于说明问题实质，这里只考虑f′和c′相关系数ρf′c′为0.0和-0.3的两种情况。当ρf′c′为0.0时可得到滑移面EFGB、DFGB、EFGC、DFGC的可靠指标分别为4.116、3.787、4.214、3.909。给滑移面失效模式编号1、2、3、4，作为两两之间相关系数ρij的下标，如EFGB和DFGB失效模式的相关系数为ρ12，利用式(7)得相关系数表如表2所示。

表1 基岩结构面参数的统计特征

表2 失稳模式相关系数表

使用Ditlevsen二阶模型法，主次结合法，蒙特卡洛法，分别进行体系可靠度计算，计算结果见表3。

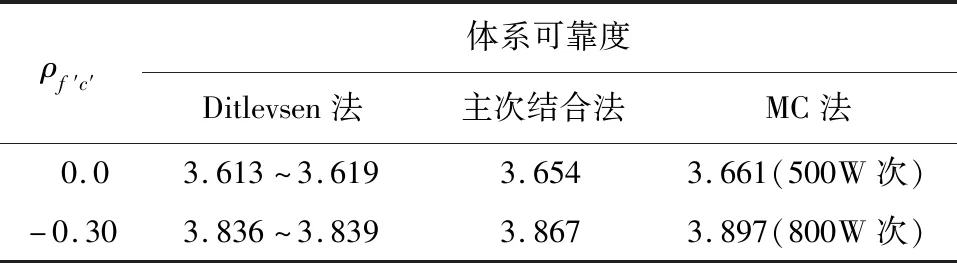
表3 体系可靠度计算结果对比

根据计算结果可知，当ρf′c′=0.0时，虽然单一滑移通道均满足目标可靠指标β=3.7的要求，但体系可靠度并不满足，可见基于多条滑移通道考虑基岩抗滑稳定体系可靠度是非常必要的；当随机变量存在负相关性时，体系可靠度增加；Ditlevsen窄界限法的界限较窄，对比蒙特卡洛法，误差在1%左右，可满足工程精度需要，主次结合法计算结果也满足工程精度要求；蒙特卡洛法需要计算多条失效路径的联合示性函数，在PC上得到一个结果需数天时间，效率较低。

3.3 基于模糊失效概率界限比的模糊可靠度分析

考虑随机变量模糊隶属函数为拟正态分布，失效准则模糊隶属函数为对称三角分布，以Rv代表随机变量模糊性对界限比R的影响，Rz代表失效准则模糊性对R的影响。根据式(5)则有R=RvRz。

(1) 考虑R值与隶属函数形式的模糊可靠度分析。首先，讨论模糊隶属度函数中参数k和α取值对模糊可靠度计算结果的影响。由于事件的模糊性随隶属函数参数k和α的增大而增强，则分别取两个参数建议值的上界和下界组成四种边界情况，即以k为0.5和3.0、α为0.01和1.00分别进行组合，得到不同隶属度时的可靠指标区间如图2所示。

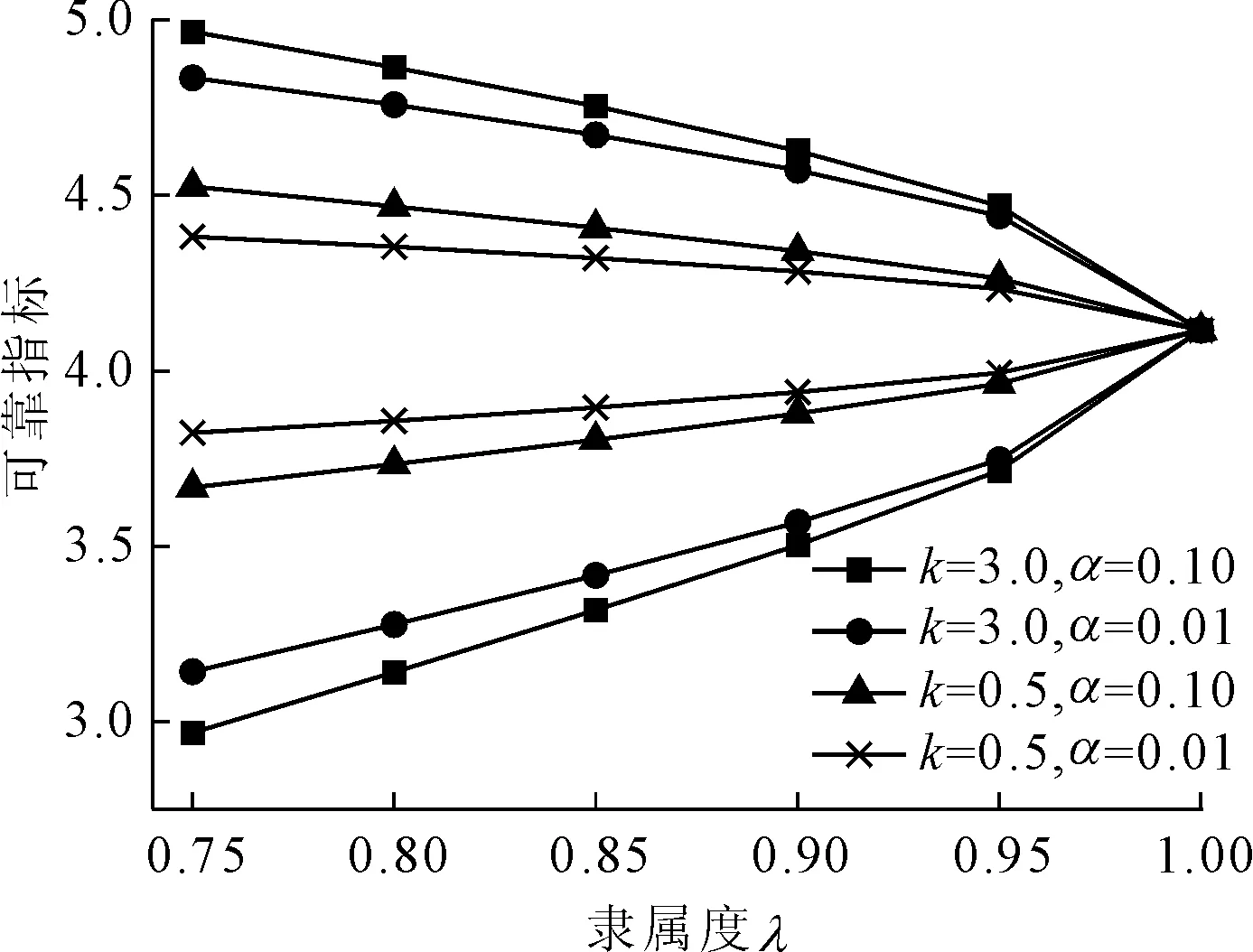
图2 隶属函数参数不同取值的可靠指标

从图2可以看出，隶属函数参数k和α的不同取值对模糊可靠指标区间范围的影响较大，其中k值的变化对最终模糊可靠度范围的影响相对显著。

然后，考虑不同隶属函数形式对模糊可靠度计算结果的影响。这里先假定当R值为定值且隶属度为λ=0.75时不同形式隶属函数的模糊性影响相同。当k=3.0，α=0.10时，本算例有Rv=1096.145，Rz=4.195。

以随机变量隶属函数为拟正态分布、三角分布，失效准则为正态分布、三角分布为例，对比不同隶属函数形式的模糊可靠度计算结果，得到不同隶属度形式组合时的可靠指标分布如图3所示。图中“拟正态-三角”表示随机变量隶属函数为拟正态分布，失效准则隶属函数为三角分布，其余以此类推。

图3 同R值下不同隶属函数的可靠指标

从图中可以看出，隶属函数的离散程度直接影响到了模糊可靠指标区间的离散程度，且随机变量模糊隶属函数变化引起的结果改变更明显，这是因为Rv远大于Rz。以给定R值讨论工程的模糊性时能得到关于隶属函数形式对可靠度计算结果的影响的更定性的结论。

(2) 基于R值的加权平均法。如若要使用加权平均法计算模糊可靠指标综合值，则失效概率的上、下界应在一个量级上以保证加权计算的合理性，即有R≤10。

以滑移通道EFGB(失效模式1)且不考虑随机变量相关性以为例，取R=9进行试算。

分析其中Rv=Rz=3的情形，经过试算得到相应的k=0.237，a=0.0766，计算此时不同隶属度的可靠指标，如表4所示。

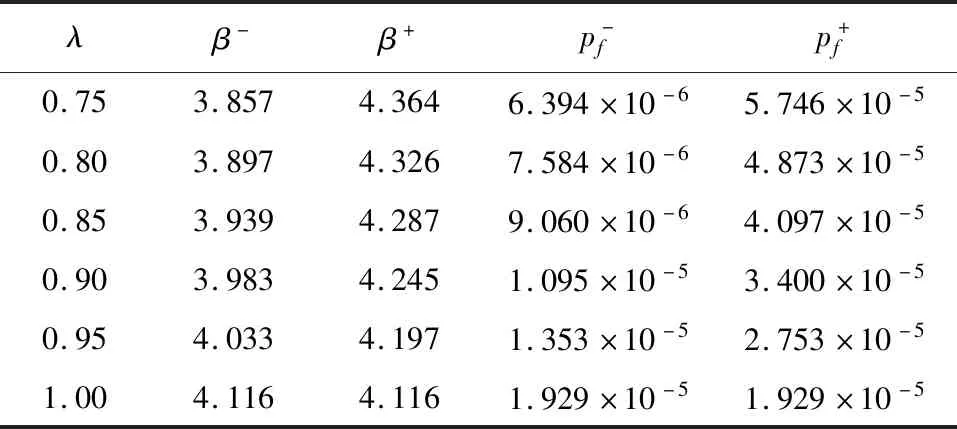
表4 模糊可靠度计算结果

对表4中失效概率加权求和，得到滑移通道EFGB的失效概率为2.457×10-5，模糊可靠指标为4.060，不考虑模糊性的结果为4.116，可见，不考虑模糊不确定性时可靠性计算结果偏于保守。

讨论本算例中随机变量模糊性和失效准则模糊性占R的比重，即Rvz的对模糊可靠地的影响，分别令Rvz为1/9和9，得到模糊可靠指标结果为4.070和4.048。Rvz从1/9增大到9时，结构的模糊性从完全由失效准则模糊性来决定过渡到完全随机变量模糊性来决定，模糊可靠指标仅减小0.5%左右，影响非常小。

若R=9且完全由失效准则决定，对其取正态隶属函数、三角隶属函数、尖Γ隶属函数，分别得到模糊可靠指标为4.004，4.057，4.072，变化并不明显，从图3可以推测，其值变化应该和隶属函数在隶属度范围内的离散程度有关。

通过上面的分析可以知道，影响模糊可靠指标的因素主要来自于R值的大小以及隶属函数的形式；而使用加权平均法后，由于同时需要对R值做假定，减小了隶属函数形式的影响。

3.4 考虑模糊性的体系可靠度计算

从兼顾精度和效率上考虑，本文使用窄界限法求解模糊体系可靠度。另外，考虑如下代表性情况：对于隶属函数的形式，随机变量的模糊采用拟正态隶属函数，失效准则的模糊采用对称三角隶属函数；对于模糊隶属函数中参数的取值，考虑边坡常用中k=3，α=0.1和k=0.5，a=0.01的两种常规情况，以及假定R=9(Rvz=1)时不同滑移通道对应不同的k和α的情况。

通过模糊可靠度计算，得到单一失效模式不同隶属度时模糊可靠度区间的上、下界值，然后采用式(6)进行体系可靠度计算，从而得到本工程的模糊体系可靠度的界限，计算结果如图4所示。

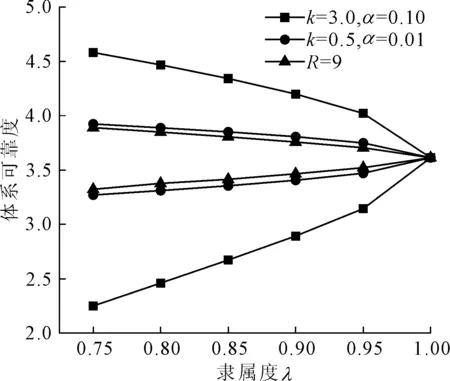
图4 不同隶属度的体系可靠指标

可见，当k=3.0，α=0.10时，得到的模糊体系可靠度区间很大。实际上当隶属度为0.75时，使用边坡工程中选取的模糊隶属函数参数的取值，计算得到的模糊体系可靠度范围为2.250～4.582，其界限比R最大达到5 301倍，使用加权平均法意义已经不大，只能作为一个粗略的参考。

借助加权平均法，计算R=9时不同ρf′c′对应不同的模糊体系可靠度，并和不考虑模糊性时的体系可靠度作为对比，由于本算例中窄界限法的区间上、下界差距不大，以其下界表示计算结果，并绘制不同隶属度时的模糊体系可靠度值，计算结果如图5所示。

图5 不同ρf′c′的模糊体系可靠度

可以看出，体系可靠度随着随机变量负相关性的增大而增大；考虑模糊时的体系可靠度值比不考虑模糊时要小，具有一定的借鉴意义。

4 结 论

本文结合模糊数学与体系可靠度理论，研究了重力坝多斜面多滑移通道坝基的抗滑稳定可靠度问题，结论如下：

(2) 若使用加权平均法，影响模糊可靠指标的主要因素是R值以及隶属函数形式，不过在规定R值的范围内，隶属函数形式的影响不大；本文工程实例对随机变量使用拟正态隶属函数时，R值随k值变化很明显，故k需要结合具体工程进行论证和选取。

(3) 窄界限法如果使用在失效概率较小的重力坝工程中，其界限很窄，参照蒙特卡洛法计算结果，其精度能满足要求；重力坝抗滑稳定问题同时考虑整体体系和模糊性后，得到的可靠指标相对较小，在协调工程安全和工程建设的经济性方面具有现实意义。