基于SOGI的IPMSM低速转子位置检测方法

赵 云， 宋茂良， 易 磊

(1 湖北工业大学 太阳能高效利用及储能运行控制湖北省重点实验室，湖北 武汉430068；2 华中科技大学 电气与电子工程学院， 湖北 武汉 430074)

永磁同步电机(PMSM)具有功率密度高、效率高和噪声低等优点，因此在空压机、新能源电动汽车等领域得到广泛应用[1-2]。机械传感器为系统提供转子位置和转速信息[3]，但其增加设计成本，同时在某些狭小的空间和极端的环境中，机械传感器不适用，因此无位置传感器控制技术具有重要的研究价值[4-5]。在内置式永磁同步电机(IPMSM)低速状态下，采用旋转高频电压注入法对其进行无位置传感器控制[6-7]，该技术的重难点之一是如何对高频响应电流信号解调。文献[8-14]针对高频响应信号解调的方法取得了一定的成果，但多个滤波器的引入，导致响应信号相位滞后且幅值衰减，从而降低转子位置观测精度。而对响应信号进行调制，增大了系统的计算量，不可避免地的给硬件造成负担。本文提出一种新型的SOGI结构进行高频电流响应信号解调，并在Simulink仿真平台上与传统信号解调方法进行对比研究，以获得更高的观测精度。

1 旋转高频电压注入法

1.1 旋转高频电压注入法基本原理

向电机αβ坐标系中注入高频电压信号，通过信号解调从高频响应电流可获取转子位置和转速信息。如图1所示，在dq坐标系中，PMSM参考电流i*dqf与反馈电流idqf比较，并经过PI调节器的调节、Park逆变换后，可得到αβ坐标系下的电压信号uαβf。给PMSM注入高频电压信号jUhejwht，其中Uh为高频电压幅值。带有高频成分的电压信号uαβh经逆变器VSI给PMSM供电，电流响应iabc经Clark变换，然后分别通过带阻滤波器(Band Stop Filters，BSF)、带通滤波器(Band Pass Filters，BPF)得到PMSM基频电流iαβf、高频电流iαβh。基频电流iαβf经过Park变换得到PMSM反馈电流idqf作用于闭环系统，高频电流iαβh通过信号解调模块获取PMSM估算转子位置角度θe。

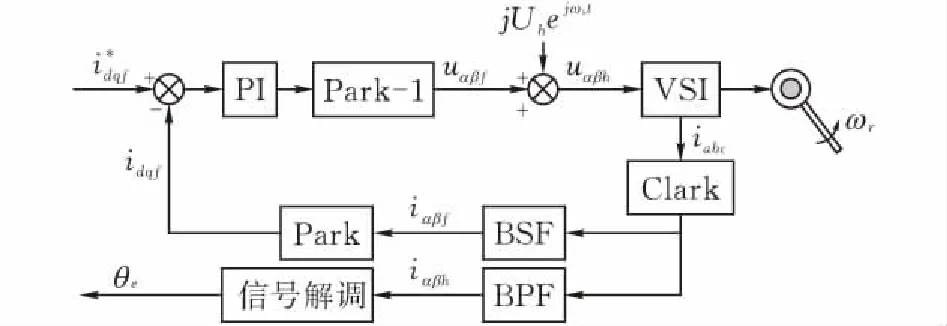
图 1 旋转高频电压注入法原理

1.2 高频注入及其电流响应

在αβ坐标系中给绕组注入高频电压信号，则PMSM的高频电压方程为

(1)

式中：uαh、uβh和iαh、iβh分别为αβ坐标系中的高频电压和高频电流；L0为共模电感，L0=(Ld+Lq)/2；L1为差模电感，L1=(Ld-Lq)/2；Ld和Lq分别为直轴电感和交轴电感；p为微分算子；θe为转子位置电角度。

将式(1)改写为电流的微分形式，则

(2)

注入的高频电压信号为

(3)

式中：ωh为高频电压的电角速度；Uh为高频电压的幅值；t为注入旋转高频电压信号的时间。

将式(3)代入式(2)，可得αβ坐标系下的电流响应为

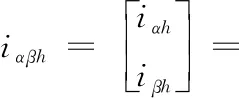
(4)

式中：Iph、Inh分别为高频电流响应的正序、负序分量幅值。

由式(4)可知，通过信号解调从高频电流响应中提取负序分量，便可获取电机转子位置信息。

2 传统的信号解调法分析

在传统的信号解调法中，采用多个滤波器对高频响应电流进行信号解调，通过外差法处理，可从负序分量中得到转子位置和转速。

图2为传统信号解调法。经Clark变换，三相电流iabc可变换为αβ坐标系下的电流iαβ，BPF可从中提取出高频电流响应iαβh。同步轴系高通滤波器(Synchronous Frame Filter，SFF)把iαβh变换到与uαh、uβh同步旋转的坐标系中，变换公式：

idqh=ej(-ωht)iαβh=Iph+Inhej2(-ωht+θe)

(5)

图 2 传统信号解调法

经高通滤波器(High Pass Filter，HPF)滤波，可获取

idqhn=Inhej2(-ωht+θe)

(6)

idqhn通过外差法模型即可获取转子位置信息和电机转速，并通过磁极判别修正，最终使得转子估算位置跟踪转子实际位置。

3 新型SOGI的信号解调法分析

在传统的滤波器信号解调法中，转子位置信息的提取通过多个滤波器的引入来实现，这给其带来了相位滞后和幅值衰减。其中，idqhn包含转子位置信息，相位滞后导致idqhn相位产生偏差，从而后续通过idqhn估算出的转子位置与实际转子位置偏离；而幅值衰减则导致idqhn的信噪比降低，增加提取idqhn的难度。

基于上述传统信号解调方法的分析，针对解决转子位置辨识精度问题，本文方案见图3。

图 3 新型SOGI的信号解调法流程图

为解决传统滤波器信号解调法中因相位滞后和幅值衰减导致估算精度较低问题，设计SOGI进行信号解调(图3)。经过Clark变换，电流iabc变换为基频电流iαβf、高频响应电流iαβh和高次谐波电流iαβc，表示为

iαβ=iαβf+iαβh+iαβc

(7)

将iαβ进行如式(5)所示的坐标变换，可以得到

idqf=ej(-ωht)iαβf=Iαβfej[(ωe-ωh)t]

(8)

idqh2=ej(-ωht)iαβh=Iph+Inhej[2(ωe-ωh)t]

(9)

idqc=ej(-ωht)iαβc=Iαβcej[(ωp-ωh)t]

(10)

式中ωp为开关装置产生的高次谐波分量角频率，其频率远高于电压注入的频率。

经过坐标变换后，静止坐标系下的电流

idqh1=idqf+idqh2+idqc

(11)

由式(8)-(11)可知，含有转子位置信息项idqhn1=Inhej[2(ωe-ωh)t]即Inhej(-2ωht+2θe)与其他项有明显的频率差异，可采用BPF进行信号提取，但常规BPF参数经过设计后，其幅频、相频特性也随之确定。通过对式(9)分析，需要筛选的频率随转子电角速度的不同而变化，故常规的BPF难以满足选频要求。

图4为SOGI的结构图，在响应电流信号提取中采用SOGI代替多个滤波器，不仅可以实现选频作用，还可以随着电机角速度的变化，自适应地改变所选频率，能够更好的实现信号的提取。

SOGI可提取出idqhn1，再将其进行坐标变换，表达式为

idqh2=ej(2ωht)idqhn1=Inhej(2θe)

(12)

从式(12)可看出，相对于以-ωh角速度同步旋转的参考系，idqh2可看做是直流量。直流量idqh2通过PLL结构即可获取转子位置信息和电机转速，再对磁极信息进行判别修正，最终使得转子估算位置跟踪转子实际位置。

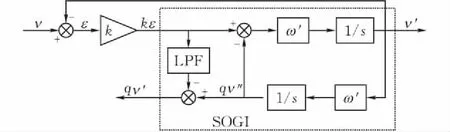
图 4 SOGI结构图

同时，由图4可知，当输入信号v含有直流分量时，输出信号v′的反馈值ε也会含有直流分量。此信号经过增益k放大，并且与qv″相减消除qv′中的直流分量。当kε引入qv″时，会产生高频谐波，在系统中引入低通滤波器(Low Pass Filter，LPF)滤除高次谐波。

新型SOGI的传递函数

(13)

式中：ω′为该滤波器的中心频率；v(s)和v′(s)分别为输入和输出信号；k为阻尼系数。

对式(13)进行改写，得

(14)

式中：QD为SOGI的品质因数。

由式(13)和式(14)，该SOGI的品质因数

QD1=1/k

(15)

对式(15)进行分析可知，新型SOGI的信号解调方法比传统滤波器方法的参数设计更简单，仅对k值进行调节就可实现系统不同的选频效果，同时也可进行系统的参数在线调试。

SOGI是先将kε经过的处理，然后与qv″做减法，从而使qv″在LPF高频段有较大的衰减，LPF传递函数为

(16)

式中τ与LPF的截止频率有关。

4 仿真与分析

为验证本文方法的可行性和优越性，在MATLAB/Simulink仿真实验平台上搭建仿真模型，分别采用传统滤波器方法和新型SOGI方法进行信号解调，所用IPMSM的参数见表1。在仿真中，注入旋转高频电压的幅值为20 V，频率为1 kHz，SOGI的阻尼系数k取0.1。

表1 电机参数

4.1 电流响应提取

在MATLAB/Simulink仿真平台中，给定IPMSM转速为100 r/min时，如图5和图6所示，可得αβ坐标系下的电流分量iα、iβ和经过新型SOGI滤波后的电流分量idhn1、iqhn1。从图5和图6可看出，新型SOGI能有效地从iα、iβ中提取含有转子位置信息的idhn1、iqhn1。

图 5 在αβ坐标系下的电流分量iα、iβ

图 6 经新型SOGI滤波后的电流分量idhn1、iqhn1

4.2 稳态误差分析

设置IPMSM空载启动，转速为100 r/min，分别采用传统滤波器法和新型SOGI法，得到100 r/min时转子位置观测和观测误差波形、转速观测和观测误差波形。由图7、图8、图9和图10可知，传统滤波器法和新型SOGI法都能实现转子位置的跟踪，采用传统滤波器法时，转子位置观测误差最大值约为0.4 rad，大约在0.3 s后观测误差趋于稳定，且稳定时误差为0.2 rad；而采用新型SOGI法时，转子位置观测最大误差约为0.15 rad，稳定时误差为0.1rad。由图11、图12、图13和图14可知，采用传统滤波器法时，转速观测最大误差约为38 r/min，稳定时误差为1 r/min；而采用新型SOGI法时，转子位置观测最大误差约为28 r/min，稳定时误差几乎为0。

4.3 动态跟踪性能分析

采用新型SOGI信号解调法实现动态跟踪性能，设置IPMSM空载启动，初始转速为100 r/min，在0.5 s时阶跃至-100 r/min，得到转子位置观测波形和转速观测波形。从图15和图16可看出，采用新型SOGI信号解调法时，转速突变后瞬间，观测转子位置和观测转速会略偏离实际转子位置和实际转速，待系统稳定后，实现动态跟踪性能。

图 8 传统滤波器法转子位置观测误差波形

图9 新型SOGI法转子位置观测波形

图10 新型SOGI法转子位置观测误差波形

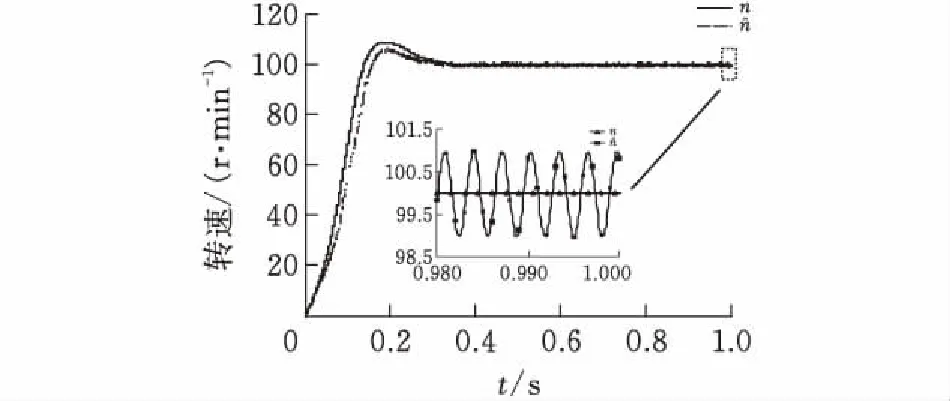
图 11 传统滤波器法转速观测波形

图12 传统滤波器法转速观测误差波形

图13 新型SOGI法转速观测波形

图14 新型SOGI法转速观测误差波形

图15 由100 r/min阶跃至-100 r/min 的转子位置观测波形

图16 由100 r/min阶跃至-100 r/min的 转速观测波形

5 结论

在旋转高频电压注入法中，传统信号解调法引入多个滤波器，导致转子位置估算产生较大误差。本文提出一种新型SOGI结构代替滤波器，将输入量和输出量进行对比的偏差直接引入输出量，并加入低通滤波器以滤除由此产生的高次谐波。此结构避免了因滤波器的引入而带来的相位滞后和幅值衰减，提高转子位置观测的精确性。同时根据估计的转速信息来自适应地改变SOGI的中心频率，从而达到提升系统位置辨识的精度和动态特性的效果。仿真实验结果表明，相较于传统方法，所提新型SOGI方法具有更佳的转子位置和转速观测性能。当系统参数突变时，该方法有较强的鲁棒性。