基于灰色关联及量子门节点神经网络的时间序列预测

黄凌霄，廖一鹏，郑秀兰

(1.阳光学院人工智能学院，福建 福州 350015；2.福州大学物理与信息工程学院，福建 福州 350015；3.福建省龙岩市气象局，福建 龙岩 364000)

0 引言

时间序列在日常生活中屡见不鲜，如股票价格、居民消费价格指数、各年度国内生产总值，以及各类食品的价格等都是随时间变化的数据序列。时间是永恒不变的变量，且各变量本身或变量与变量之间的不明确的变化关系，使得时间序列的处理难度大。时间序列分析方法是预测领域中的重要工具之一，它主要通过建立相关模型描述历史数据随时间动态变化的规律以预测未来的值[1-3]。灰色系统理论作为一种专门研究含不确定因素的系统的新方法，已被广泛地应用到时间序列的预测当中。同时，新生的量子神经网络在寻找时间序列的变化方式和演化规律方面已经逐步取代了传统的预测方法。

1982年邓聚龙教授提出了灰色系统理论，该理论被用来解决产量的预测，指标的评价，价格的变化与控制等问题[4-5]。基于灰色系统理论，研究者们提出了GM(1,1)，GGM(1,1)，DGM(1,1)等预测模型，逐步改善了均质指数模拟偏差、原始方程与白方程之间的不平衡转换、预测不够稳定等问题[6]。在生产生活中，张恩路等将灰色理论运用到求解漂移型价格的最优解的问题中[7]；在理论研究方面，郝艳捧等基于灰色关联分析建立了质量评价体系；在数据预测方面[8]，张和平等提出灰色关联度分析的组合预测模型并应用到GDP预测中[9]，曾波等通过数学建模方法实现了对小样本振荡数据取值范围的模拟与预测[10]。

神经网络作为一种基于误差反向传播的多层前馈网络技术，对时间序列预测有着特殊的作用[11]。张思源等利用BP神经网络建立了预测模型，解决了钢铁冶炼能耗高的问题[12]；黄俊铭等通过RBF神经网络有效地模拟了综合负荷功率的动态微分变化过程[13]；关海鸥等基于量子神经网络，成功解决了农村低电网中不能检测出残留电流和电路故障的难题[14]。

单一预测模型由于自身的限制，影响了预测结果，对此，许多学者提出了组合模型。张敬祎等建立基于时间序列与灰色理论的油料组合预测模型，预测精度更高、误差更小[15]；杨利纳等提出灰色遗传BP神经网络，对校园区间需水进行预测，验证了可行性[16]；张水等将灰色-RBF网络模型用于瓦斯涌出量预测，预测精度明显高于单一模型预测[17]。但是传统神经网络有收敛速度慢、易陷入局部最优且训练结果不稳定等缺点，新兴的量子神经网络融合了量子计算的并行特性和神经网络的优点[18]，增强了计算能力和自适应能力，具有较好的网络收敛效果和预测能力。

本文结合灰色系统理论、神经网络与时间序列预测，建立灰色关联分析与量子门节点神经网络的组合模型，分析模型的合理性，通过实例验证了该模型的有效性和可行性，为时间序列预测提供了新的思路和方向。

1 灰色关联分析模型

灰色系统理论是一种研究少数据、贫信息、不确定性问题的新方法，已成为许多领域进行系统分析、建模、预测、决策、控制的新思路。灰色关联分析是灰色系统理论中最活跃的一个分支，其基本思想是根据参考序列与比较序列的曲线形状的接近程度做变化趋势分析，曲线越接近, 则两序列的关联度就越高，反之则越小。灰色关联分析由于自身计算量小、适应性强以及原理简单等优势，使得它的发展速度远超过灰色系统的其他分支，更被普遍地应用到生活中。

王世元等对灰色关联分析的原理和计算方法进行了充分讨论[19]，主要计算步骤如下：

1)初值像矩阵相减得差序列为：

Δ0i(k)=|x′0(k)-x′i(k)|

(1)

其中，各变量分别由以下公式计算得到：

xi=(xi(1),xi(2),…,xi(k),…)

(2)

x′i=(xi(1)/xi(1),xi(2)/xi(1),…,xi(k)/xi(1),…)=

(x′i(1),x′i(2),…,x′i(k),…) (i=0,1,2,…,m)

(3)

Δ0i(k)=(Δ0i(1),Δ0i(2),…,Δ0i(k),…) (i=1,2,…,m)

(4)

其中，xi(k)表示i因素的第k个原始数据，x′i表示原始数据的像矩阵。

2)关联度计算为：

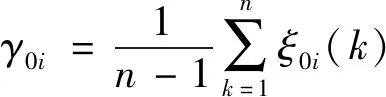
(5)

2 基于梯度下降法的量子门节点神经网络

传统的神经网络以其独特的优势已经被成功地应用到很多领域。然而，随着信息处理量和复杂度的不断增加，人工神经网络的训练能力差、计算速度不够高等缺点已不能满足要求，20世纪90年代美国路易斯安那州立大学的Kak教授提出了量子神经网络，该算法结合了量子计算和神经网络的优点，收敛速度快，更好地解决了现代科学研究信息量大、数据复杂等问题。之后，很多思想和模型不断被提出，如量子人工神经网络、量子衍生神经网络、量子点神经网络、基于量子通用门神经网络和量子门节点神经网络模型等。其中，量子门节点神经网络是一种具有代表性的新型量子神经网络，本文将它与梯度下降学习算法相结合，寻找待研究参变量的最优值。

2.1 量子门节点神经网络

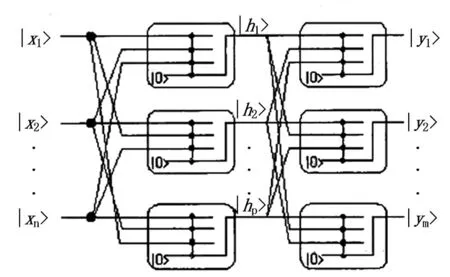
图1 量子门节点神经网络图Fig.1 Diagram of quantum gate node neural network

量子门节点神经网络[20]的原理如图1所示。图中|x1>,|x2>,...,|xn>为输入，|h1>,|h2>,...,|hp>为隐含层输出，|y1>,|y2>,...,|ym>为网络输出。

1)令输入样本的量子态为：

(6)

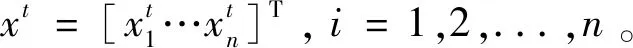
2)根据量子旋转门与多位受控门可得：

(8)

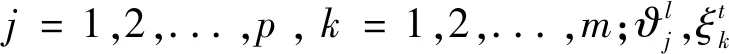
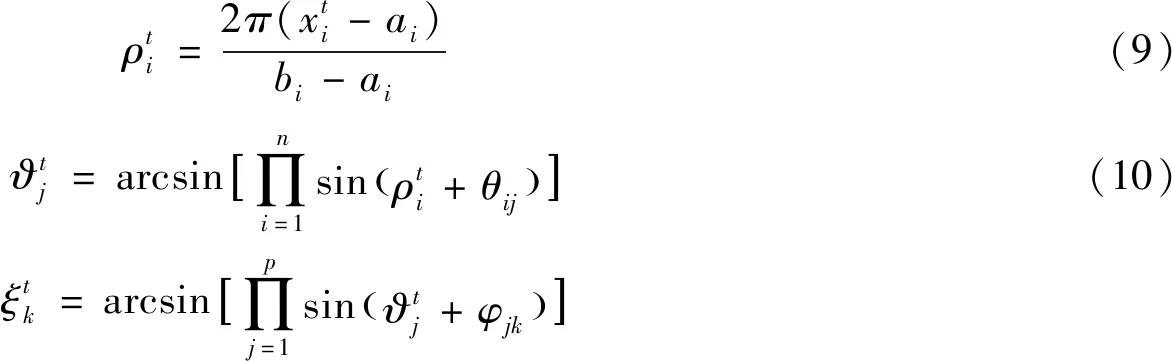
(11)

3)若以各层量子位的状态|1〉作为本层的实际输出，则各层实际输出为：

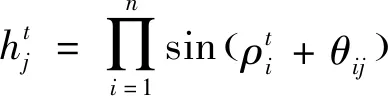
(12)

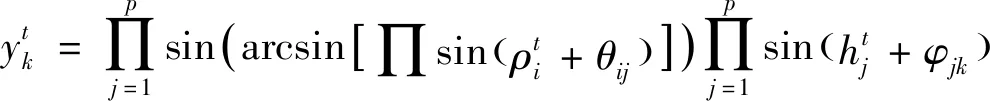
(13)

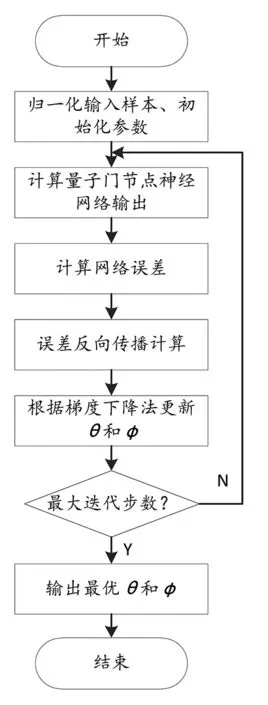
图2 量子门节点神经网络算法流程图Fig.2 Flow chart of quantum gate node neural network algorithm

2.2 网络模型

本文利用梯度下降法实现量子门节点神经网络的计算，建立网络模型，精确定位和计算量子门节点神经网络隐含层幅角偏置矩阵θ和网络输出层幅角偏置矩阵φ的全局最优解，实现流程图如图2所示，具体步骤如下。

1)输入样本归一化以及网络参数初始化

首先，有T0个输入样本的量子幅角矩阵为：

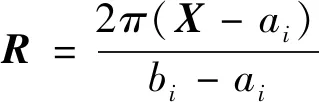
(14)

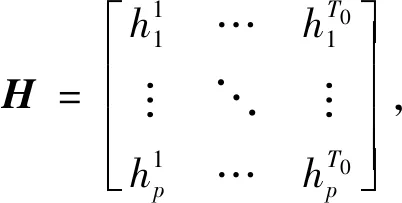
2)计算量子门节点神经网络的输出。对于r=1→T0，有：

(16)

3)计算神经网络的误差，采用Frobenius范数表示为：

4)误差反向传播计算。

首先，对于r=1→m，E对φ的第r列的偏导数为：

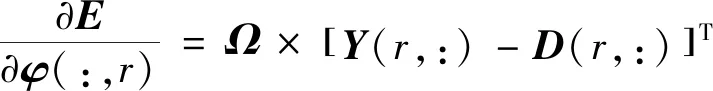
(17)

其中，Ω为p×T0的中间变量矩阵：

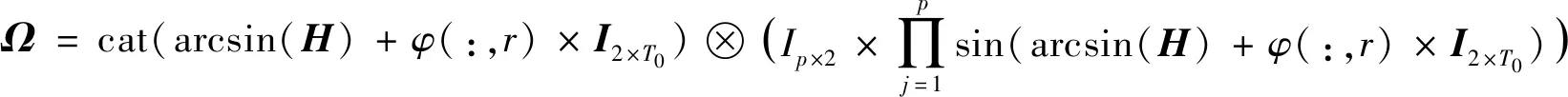
(18)

其次，对于r=1→p，E对θ的第r列的偏导数为：

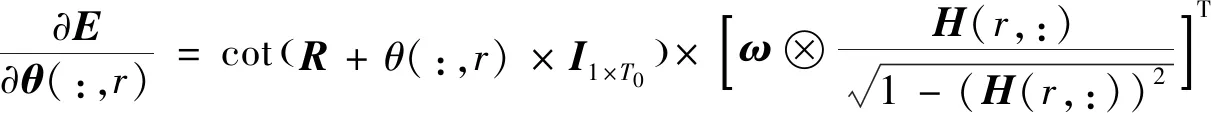
(19)

其中，ω为1×T0的中间变量矩阵：

ω=sum[cot(Im×1×arcsinH(r,:))+(φ(r,:)T×I1×T0)⊗(Y-D)⊗Y]

(20)

5)根据梯度下降法更新θ和φ，见公式(21)和公式(22)，其中，α表示学习步长。

(22)

6)判断是否达到迭代结束条件，若是，则退出循环；否则，转至第2步继续循环。

3 灰色关联-量子门节点神经网络模型实现步骤

为充分发挥灰色关联分析与量子门节点神经网络各自的优势，将二者结合起来分析和预测给定时间序列的变化情况。实现流程图如图3所示，具体步骤如下：

图3 预测算法流程图Fig.3 Flow chart of predictive algorithm

Step 1将待研究时间序列X1和影响因素序列X2、X3、…、Xn整合起来，组成一个列为样本，行为指标的待处理原始数据序列Data0。

Step 2对Data0进行灰色关联分析，显示并分析各影响因素与待研究时间序列的关联度的大小，并对关联度进行排序得到灰色关联序。

Step 3为更直观地观察待研究时间序列与各影响因素的关系，根据Data 0做出X1与X2、X3、....、Xn的变化率曲线图。

Step 4根据灰色关联序，判断并删除小于关联度阈值为0.8的原始数据列(一般关联度大于等于0.8时，待研究时间序列与各影响因素关联度很好)，并将Data0更新为Data1。

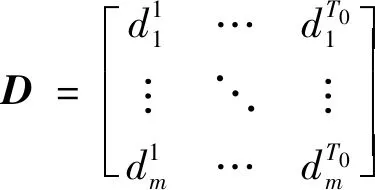
Step 5以Data1为有效信息资源，导入量子门节点神经网络进行充分学习和训练，计算预测结果Y1和预测误差α1，并记录运算时间T1。

Step 6以Data0为有效信息资源，导入量子神经网络进行充分学习和训练，计算预测结果Y2和预测误差α2，并记录运算时间T2。

Step 7以Data0为有效信息资源，分别导入传统的BP神经网络和RBF神经网络进行学习和训练，计算预测结果Y3和Y4以及预测误差α3和α4，并记录运算时间T3和T4。

Step 8以Data1为有效信息资源，分别导入传统的BP神经网络和RBF神经网络进行学习和训练，计算预测结果Y5和Y6以及预测误差α5和α6，并记录运算时间T5和T6。

Step 9通过列表定量分析、对比Step 5、Step 6、Step 7、Step 8所得的结果，并得出结论。

4 实验结果与分析

以我国城市居民消费体系价格指数(CPI)为研究对象，硬件平台为AMD Ryzen 5 2500U with Radeon Vega Mobile Gfx 2.0GHz、8.00GB(RAM)，软件环境为Windows 10 Matlab R2014b。通过实验验证本算法的性能，并对实验结果进行深入的分析和对比。

以我国2017年2月至2018年2月的城市居民消费体系价格指数(CPI)为研究对象(Data0)，完整数据如表1所示。

以城市居民消费价格指数X1作为参考序列，以影响CPI的8个影响因素(X2～X9)作为对比序列。根据上述灰色关联度的计算方法，求出CPI与各影响因素之间的关联度，并得到大小顺序，结果如表2所示。

同时做出参考序列与对比序列的变化率曲线图，图4为CPI与影响因素X2～X5的变化率曲线图，图5为CPI与影响因素X6～X9的变化率曲线图。

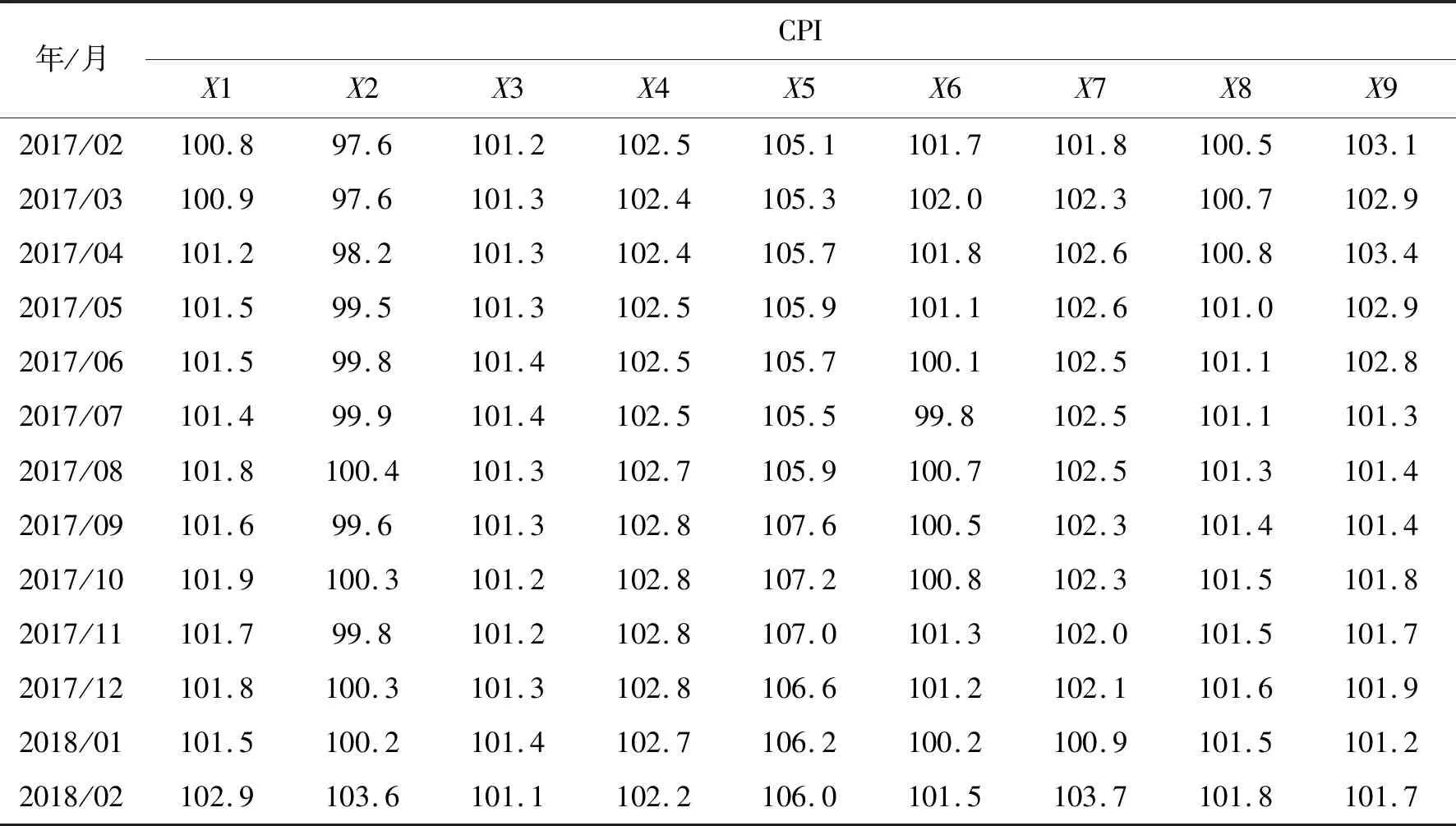
表1 居民消费体系价格指数(CPI)Tab.1 Consumer system price index (CPI)

表2 CPI灰色关联分析结果Tab.2 Analysis results of CPI grey relational analysis

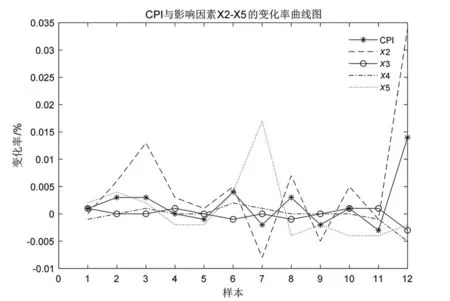
图4 CPI与影响因素X2～X5的变化率曲线图Fig.4 Change rate curve of CPI and influencing factors X2～X5

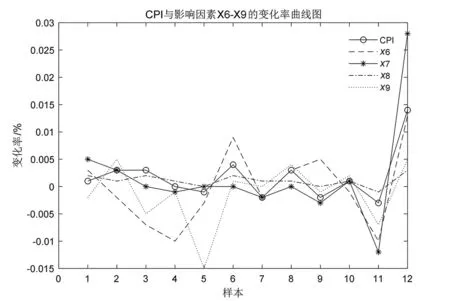
图5 CPI与影响因素X6～X9的变化率曲线图Fig.5 Change rate curve of CPI and influencing factors X6～X9

从得到的数据结果可以看出，本文选取的8种因素影响程度的灰色关联序列为：X4>X5>X8>X2>X7>X3>X6>X9。在2017年2月至2018年2月期间，影响我国CPI的8种因素当中，X4因素影响最大，X5、X8因素的影响也较显著，X6、X9因素的影响力有限，关联度分别只有0.787 08和0.738 74，小于关联度阈值0.8。于是根据步骤step 4删除二者所对应的原始数据列，并将Data0更新为Data1。

为了对比的需要，选取样本点2017年8月到2018年2月(共7个)，分别以原始序列Data1和Data0作为量子门节点神经网络和量子神经网络的输入数据，进行充分学习和训练，由步骤step 5和步骤step 6得到预测值分别为Y1和Y2，CPI预测值与真实值的曲线拟合结果如图6和图7所示。

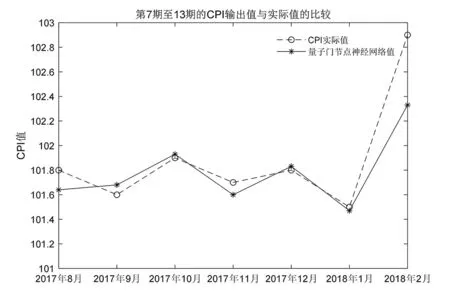
图6 预测值与原始数据的散点折线图Fig.6 Scattered point polygraph between predicted vlue and original data

图7 预测值与未处理原始数据的散点折线图Fig.7 Scattered point polygraph between predicted value and unprocessed raw data

为了验证此算法的预测精确度，本文引入了误差分析，根据预测值和实际值求出相对误差均值，公式如下：

(23)

其中，E为相对误差；n为预测样本数，vp为预测值；vr为真实值。

根据公式(24)可以求出预测误差均值，记录的平均预测误差α1为0.289 1、α2为0.291 2，平均运算时间为T1为49.12 s、T2为114.7 s。

为比较不同算法的预测性能，分别采用文献[12]算法、文献[13]算法、文献[14]算法、文献[16]算法、文献[17]算法及本文算法对序列进行预测，得到预测性能综合评估分析如表3所示，以此来衡量各类算法的性能。

表3 不同算法预测性能综合评估表Tab.3 Comprehensive evaluation table for prediction performance of different algorithms

由表3可以看出，文献[12]和文献[13]采用传统的神经网络，预测时间较短，但由于预测可持续性差导致平均预测误差较大，从图6和图7可以看出，前期预测值曲线与真实值曲线重合度较高，后期预测值曲线的波动逐渐变大；文献[14]采用量子神经网络方法，由于算法本身需要多次迭代，故所需的预测时间较长，但平均预测误差比传统的神经网络小；文献[16]和文献[17]采用灰色关联与传统神经网络相结合的方法，预测时间较短，但预测误差改进不是很理想；本文提出的灰色关联分析与量子门节点神经网络相结合的预测模型，预测时间不仅相对于单独采用量子神经网络方法降低较多，预测误差还更小。综上，本算法与传统的神经网络模型相比稳健性更高，可在有限小样本情况下表现出较好的预测效果，该方法不仅降低了时间序列预测时间，还使预测误差稳定在可接受范围之内。

5 结论

本文提出的灰色关联分析与量子门节点神经网络的组合预测模型，通过灰色关联分析计算时间序列的关联度，合理删除关联度小于阈值的原始时间序列，以达到降低数据量的目的；以更新后的时间序列作为输入，通过梯度下降学习算法准确找到量子门节点神经网络的全局最优值，对神经网络起到优化作用；最后，得到了时间序列预测值与原始数据比较的散点折线图，并记录了预测时间和预测误差。实验结果表明，与传统的单一预测方法相比，在需要同时考虑时间效率和可接受预测误差的时间序列预测中，本算法提供了一个较好的选择。