一阶速度-应力双相介质方程逆时偏移及GPU 加速实现

张晓波,刘保华,于凯本,刘 苗,杨志国,于盛齐,宗 乐

(1.自然资源部 国家深海基地管理中心,山东 青岛266237;

2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室,山东 青岛266061;3.中国海洋大学 环境科学与工程学院,山东 青岛266100;4.青岛海洋科学与技术试点国家实验室 公共关系部,山东 青岛266061)

逆时偏移算法出现于20世纪80年代早期[1-2],其基于双程波动方程理论而不需要对波动方程进行分解,避免了因对波动方程近似而造成的倾角限制,因此该方法是公认的对复杂构造的理想成像方法,一直以来都是地球物理领域的研究热点。Chang和Mc Mechan首先将二维逆时偏移推广到弹性波领域[3],随后又将其推广至三维情况[4-5];张会星等[6]基于程函方程实现了多波多分量资料的逆时偏移。为有效压制逆时偏移的层间反射,何兵寿等[7]发展了任意广角声波方程逆时偏移技术;Yoon等[8]将Poynting矢量成像条件引入到逆时偏移中;Sun等[9]提出在纵横波场分离的基础上实现弹性波逆时偏移。针对逆时偏移的大存储量问题,Clapp[10]、王保利等[11]利用随机边界以及吸收边界存储策略降低了常规逆时偏移方法中存储空间消耗;石颖等[12]就随机边界条件和吸收边界条件在逆时偏移算法中的应用效果以及相应的4种存储策略展开具体分析,给出了不同存储策略下的计算成本和存储量需求。

经过近几十年的发展,逆时偏移已逐渐由模型实验走向实际生产,但在部分富含油气的复杂构造区域的偏移成像上遇到困难,其主要原因是这类区域往往具有双相介质的特性[13],而当前常规的逆时偏移算法多基于声波和弹性波等单相介质理论,无法对具有双相介质特性的地下构造进行准确成像[14]。因此,要实现双相介质特性区域的精确成像需基于双相介质理论波动方程进行逆时偏移处理,在此方面目前已有学者进行了初步的尝试和探讨,刘欣欣等[15]基于二阶双相介质方程实现了双相介质的逆时偏移。其实验结果显示,对于双相介质区域,双相介质方程逆时偏移比弹性波逆时偏移更具优越性。

虽然双相介质逆时偏移技术更适合复杂油气构造区域的成像处理,但由于双相介质方程比声波和弹性波方程更为复杂,因此其计算效率低下,难以适应大规模实际生产的要求。近年来,GPU(Graphics Processing Units)凭借其优异的浮点运算能力和更快的访存速度已成为解决大计算量问题的新兴高性能运算工具。自CUDA(Computer Unified Device Architecture)推出后,GPU 加速运算在地球物理领域得到广泛推广,目前已有学者将其引入逆时偏移领域用以解决计算效率的问题[16-17]。朱博等[18]实现了基于多卡GPU 集群的多次波逆时偏移成像处理;Foltinek等[19]研究了二维和三维声波逆时偏移的GPU 加速效果;刘红伟等[20]详细分析了二阶声波方程逆时偏移的GPU 加速效果;马庆珍[21]研究了弹性波逆时偏移的关键技术和GPU 加速技术。上述研究成果表明,声波和弹性波逆时偏移的GPU 加速均可获得几十倍的加速比。由于波动方程逆时偏移的实现过程具有相似性,因此可以预见,应用GPU 加速将可显著提高双相介质逆时偏移的计算效率,使其能够早日服务于生产。

本研究基于Biot双相介质理论[22]实现了二维一阶速度-应力双相介质方程逆时偏移及其GPU 加速,并利用模型实验验证了基于GPU 加速的双相介质方程逆时偏移的优越性。

1 双相介质方程逆时偏移算法

根据Whitemore[1]所提出的在时间域进行波场重建的逆时偏移理论,双相介质逆时偏移首先需应用双相介质方程的有限差分波场延拓方法得到炮点正向波场和检波点逆时波场,然后根据互相关成像条件得到地下每个网格点的成像值。

1.1 基于一阶速度-应力双相介质方程组的波场延拓

常规的双相介质方程逆时偏移波场延拓多基于一阶速度-应力双相介质方程组的交错网格有限差分实现,其在二维情况下的表达式为

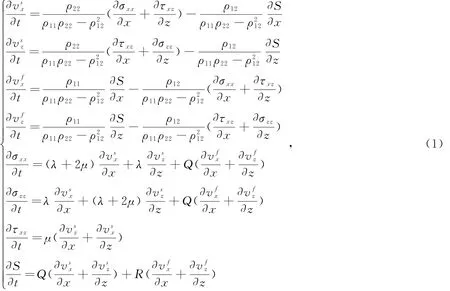
式中,x,z分别代表空间的横向坐标和纵向坐标;vs=(vsx,vsz)T为固相的速度向量,vf=(vfx,vfz)T为流相速度向量,σxx,σzz,txz为固相应力张量,S为流相有效压力;ρ11表示固体相对流体运动时固体部分的等效质量,ρ22表示流体相对于固体运动时流体部分总的等效质量,ρ12表示流体和固体之间的质量耦合系数;λ,μ为双相介质中的拉梅常数,R为流相弹性参数,Q为固相体积与流相体积变化之间的耦合关系。当前,在基于式(1)进行波场延拓数值计算时,通常采用高阶有限差分方法以满足计算精度的需要。因此,需结合时间2阶、空间2N阶交错网格有限差分计算方法,进一步得到相应的一阶速度-应力双相介质方程组交错网格有限差分格式[23]。

同时,为了提高波场模拟的精度,在逆时偏移波场延拓时需引入人工边界条件以消除边界反射,这里采用PML吸收边界条件方法实现。该方法通过在计算区域外面构造有限厚度的吸收层,并在吸收层内设置衰减因子,从而使地震波在吸收层内传播时能量不断衰减。在式(1)所示的双相介质方程中引入衰减因子后,相应的PML边界条件如下式所示:

基于式(1)和式(2)所对应的交错网格有限差分表达式,若以震源子波作为正向扰动,从初始时刻计算至最大时刻,即可实现双相介质方程的波场正向延拓,从而获得正向波场值;若以地震记录作为逆时扰动,从最大时刻逆向反推计算至初始时刻,则能够实现双相介质方程的波场逆向延拓,从而得到逆时波场值。

1.2 归一化互相关成像条件

采用归一化互相关成像条件实现偏移成像[25],其主要过程是利用震源波场的零延迟互相关的结果对正向与逆向波场零延迟互相关成像的结果进行归一化:

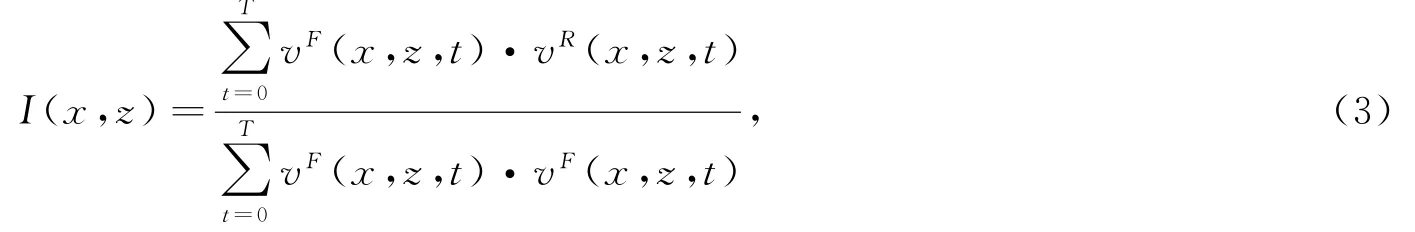
式中,vF为正向波场,vR为逆向波场。

利用以上成像条件成像时需要每一时刻的正向波场值。当模型较大时,若将这些波场值全部保存在存储介质上,不仅需要大量的存储空间而且需要较长的数据存取时间。为了克服这个问题,本研究采用基于PML的有效边界存储策略[11]存储震源波场正向延拓时每一时刻各边界上PML 边界内与中心波场邻接的N(当空间为2N阶精度差分时)层网格点的波场值以及最后一个时刻的中心波场值,然后在沿时间反向传播时将这些边界波场值取出并作为边界条件即可逐一恢复正向波场。这种方法虽然需要事先进行1次震源波场正向延拓,但这能有效降低逆时偏移的存储量。由图1可见,在震源波场正向和逆向延拓中,基于PML边界条件的有效边界存储策略流程。

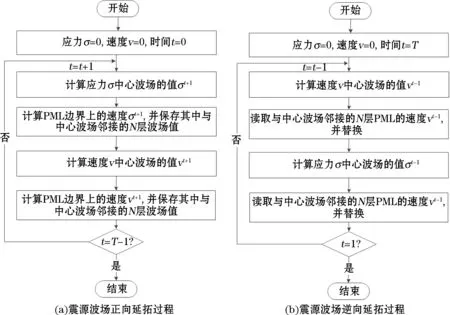
图1 基于PML边界条件的有效边界存储策略流程Fig.1 Flowchart of effective boundary storage strategy based on PML boundary conditions

2 基于GPU 加速的双相介质方程逆时偏移算法

逆时偏移为典型的密集运算地球物理问题,而双相介质方程逆时偏移的计算量又远大于声波方程和弹性波方程逆时偏移的计算量,因此若仅基于传统的CPU 计算设备运算,其计算效率难以满足实际生产的需要。

当前GPU 凭借其优异的浮点运算能力和更快的访存速度已成为新一代的高性能计算工具,并且随着计算机技术的快速发展,GPU 卡的性能不断提高。2013年NVIDIA 公司推出的Tesla K40卡,其流处理器已达到2 880个,每秒可执行约4.29万亿次浮点运算,并且其显存带宽达到288 GB/s。本研究利用Tesla K40卡实现双相介质方程逆时偏移的GPU 加速。

2.1 CUDA编程模型

GPU 加速目前多基于CUDA 平台实现。CUDA 编程模型的主要思想将CPU 作为主机(Host),GPU作为设备(Device)。在1个系统中可以有1个主机和多个设备,其中CPU 负责向GPU 分配任务和串行计算,GPU 负责执行线程化并行计算,此外两者拥有相互独立的存储器(CPU 端为内存和GPU 端为显存)。

在GPU 上运行的函数称为Kernel(内核)函数。一个完整的CUDA 程序是由主机函数和一系列Kernel函数共同组成的。主机函数的工作包括在Kernel函数启动前进行的数据准备、设备初始化以及在Kernel函数之间进行的一些串行化计算。执行Kernel函数所需的GPU 线程是以线程网格(Grid)的形式组织的,每个Grid又由若干个线程块(Block)组成,每个Block又由若干线程(Thread)组成,线程层次如图2所示。调用时需要设定Kernel函数中Grid的Block数目以及每个Block中Thread的数目,而Block中的线程数需要根据GPU 的计算能力来合理配置以充分发挥GPU 多线程并行计算的潜力,因为Tesla K40卡的计算能力已达到3.5,因此在计算时将线程数设置为512(即该卡设计最大可用值)。

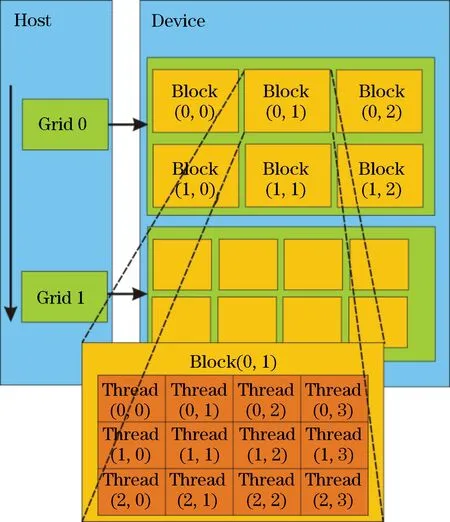
图2 GPU 线程示意图[18]Fig.2 Diagram of GPU thread[18]

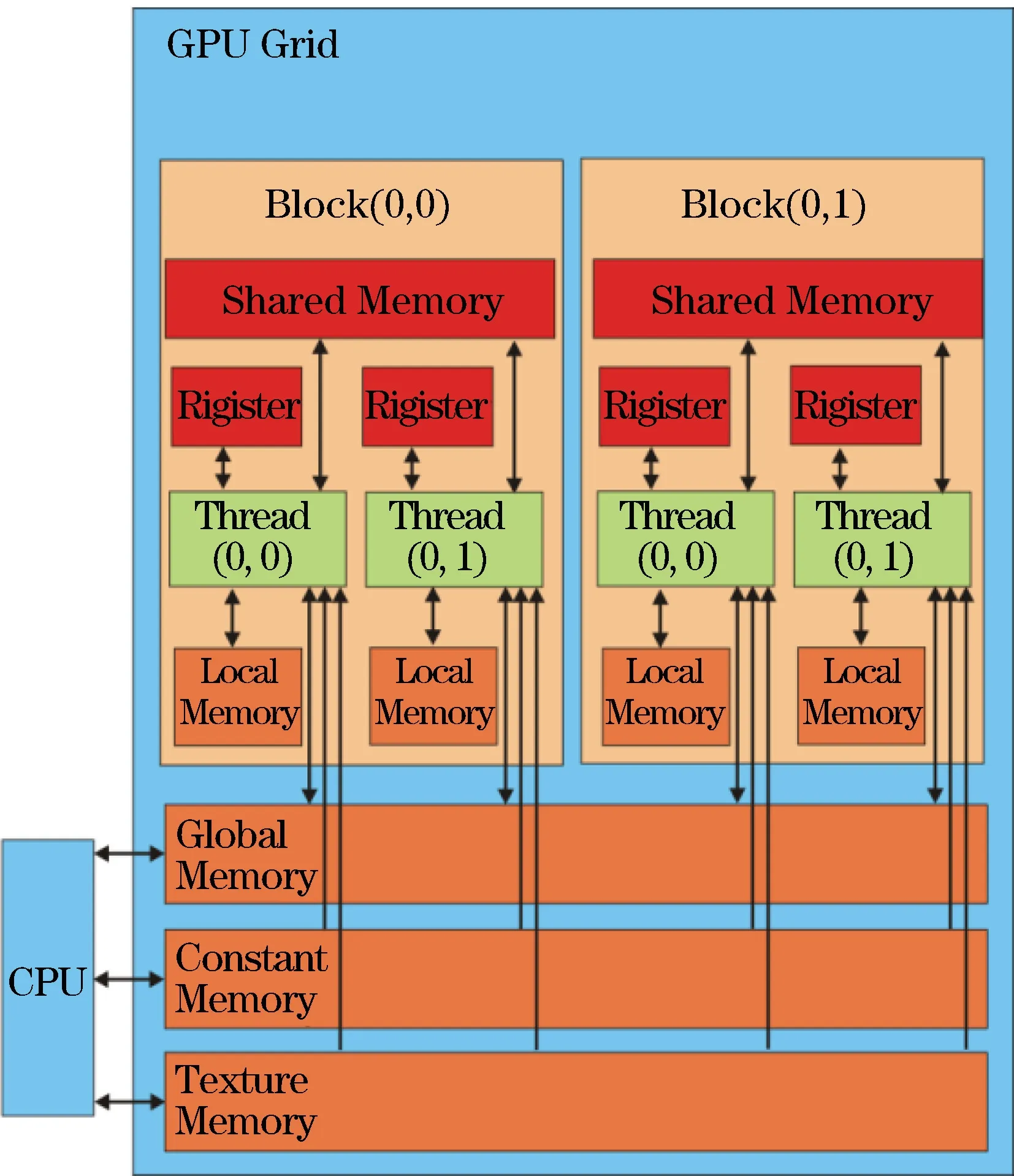
图3 CUDA 存储器模型[18]Fig.3 CUDA memory model[18]

除了线程层次以外,CUDA 编程模型中还规定了一系列用于控制CPU 通信与GPU 通信所需存储空间的存储器模型(图3),主要包括寄存器(Rigisiter)、局部内存(Local Memory)、共享内存(Shared Memory)、常量内存(Constant Memory)、纹理内存(Texture Memory)和全局内存(Global Memory)等部分。其中,共享内存、常量内存等访存速度较快,能够显著提高GPU 的计算效率,但其存储空间较小,因此在本文中将内存消耗较小的有限差分格式的差分系数数组应用共享内存进行存储,同时将炮和道的位置坐标数组等内存消耗也相对较小的参量应用常量内存进行存储;纹理内存适合存储需频繁进行地址访问的只读参量,因此本文将空间波场的数组应用纹理内存进行存储;此外,由于其余参量数据量巨大而且需要频繁修改,因此采用全局内存。

2.2 主机函数和核函数配置及CUDA 伪码

双相介质方程逆时偏移流程的步骤主要包括:速度模型输入、震源子波赋值、接收点记录输入、震源波场正向延拓、震源波场逆向重建、检波点波场逆向延拓、吸收边界条件处理、震源波场边界存储、震源波场边界输入和互相关成像等。其中震源波场正向延拓、震源波场逆向重建、检波点波场逆向延拓、吸收边界处理以及互相关成像属于密集运算问题,应通过调用Kernel函数来借助GPU 计算,而其余步骤应采用CPU 计算。本研究基于以上分析设置了相关的主机函数和核函数,具体名称和功能见表1,核函数前缀为“__global__”,同时给出了基于CUDA 的双相介质方程逆时偏移程序伪码(图4)。

图4 基于CUDA 的双相介质方程逆时偏移程序伪码Fig.4 Pseudo code for reverse time migration of dual phase medium equation based on CUDA

表1 主机函数及核函数表Table 1 Host function and kernel function

3 模型实验与分析

3.1 基于GPU 的双相介质方程逆时偏移模型实验

使用双相介质模型(图5a)进行双相介质方程逆时偏移的实验,模型介质参数如表2所示,其中第7,8层为双相介质地层。模型中双相介质地层由于孔隙流体的存在(孔隙率＞0),其表示液相及固液耦合相的参数Q,R,ρ22以及ρ12等均不为0。模型水平方向长度为2 500 m,垂直深度为1 000 m,空间网格大小为5 m×5 m;本实验采用双边观测系统,炮点深度为5 m,炮间距10 m,总炮数为300炮;接收点深度为5 m,每炮接收道数为100道,道间距5 m。使用雷克子波作为震源函数,子波主频为40 Hz。利用双相介质方程实现基于GPU 的逆时偏移,并得到固相垂向速度分量偏移剖面如图5b所示。

表2 复杂模型双相介质模型弹性参数Table 2 Elastic parameters of dual-phase medium model of complex model

目前实际生产中常用的逆时偏移方法多基于弹性波方程或声波方程实现。为比较其与双相介质方程逆时偏移效果,本研究根据双相介质参数与弹性波介质参数以及声波介质参数的关系[26-27],从表2所示的双相介质参数中分别提取弹性波介质参数和声波介质参数并由此实现基于弹性波方程以及声波方程的逆时偏移(偏移剖面分别如图5c和图5d所示)。为便于3种方法所得结果的对比分析,这里分别将图5中对应于双相介质区域的模型和剖面进行放大显示(图6)。

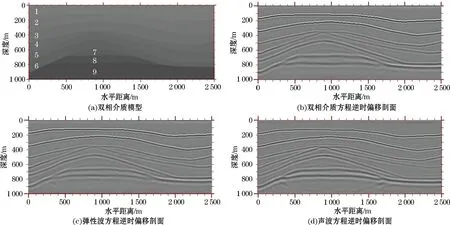
图5 双相介质模型及逆时偏移剖面图Fig.5 The dual-phase medium model and reverse time migration profiles

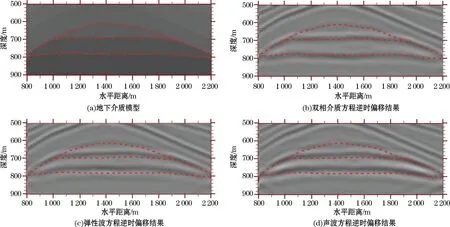
图6 偏移剖面局部放大对比图Fig.6 Partial enlarged drawing of reverse time migration profile

由图5b,5c,5d和图6可知,在非双相介质的地层处,弹性波方程与声波方程均能较好的描述构造的形态,而在双相介质假设的地层处,其偏移剖面的构造形态则与介质模型存在明显差异,其主要原因为单相介质中未考虑填充在固体介质孔隙中的流体对介质参数的影响,这就使得单相介质模型参数与双相介质模型参数之间存在差异,其会导致波的传播过程出现偏差,从而影响成像点的位置和成像质量。而对于双相介质逆时偏移来讲,无论是在双相介质区域还非双相介质区域,其均可精确成像,这说明双相介质逆时偏移方法对双相介质地层成像的有效性。

此外,本研究的模型实验显示,基于Tesle K40卡的双相介质逆时偏移其计算时间仅为1 860 s,而基于型号为Intel Core i5-2400 的CPU 其计算时间则需约50 400 s,其加速比可达到27倍,这说明与常规基于CPU 平台的算法相比,GPU 加速技术能够显著提高双相介质逆时偏移的计算效率。

4 结 论

基于一阶速度-应力双相介质方程实现了基于GPU 加速的逆时偏移,通过理论分析和数值实验可以得出如下结论:

1)无论是在双相介质区域还是在非双相介质区域,双相介质逆时偏移均可精确成像,这说明双相介质逆时偏移方法对双相介质地层成像的有效性;

2)与常规基于CPU 平台的算法相比,应用GPU 加速技术的双相介质逆时偏移可达到27倍的加速比,能够显著提高双相介质逆时偏移的计算效率。