薄弱层对钢框架结构抗震性能影响分析

郑文豪

(北京市市政工程设计研究总院有限公司 100082)

引言

结构刚度(Stiffness of Structure, Rigidity of Structure)是建筑结构所拥有的固有性质之一，其内在本质是结构抵抗荷载作用下发生变形的能力。对于抗震结构而言，结构需要具有必要刚度的抗侧力系统以实现直接承受地震作用、控制结构侧向变形、防止非结构构件(如填充墙、隔墙和幕墙等)产生明显损伤以及保证结构的抗震性能等目标。而实际工程中因建筑外观及功能性等因素的影响，结构常表现为侧向刚度分布不均。大量的震害表明，结构的侧向刚度分布不均对结构抗震性能影响较大，导致结构破坏模式发生改变。

地震易损性是指在给定强度的地震作用下，结构达到或超过某种破坏状态时的条件失效概率，常以易损性曲线或破坏概率曲线进行表征，以此来对结构做抗震性能的综合性评估。基于此本文分别建立了首层薄弱、中层薄弱及顶层薄弱结构，对这3个结构进行了地震易损性分析来探究竖向刚度不均对结构抗震性能的影响，以期为钢框架结构抗震设计提供一定参考依据。

1 地震易损性分析方法

易损性曲线是对结构处于不同破坏状态可能发生概率的定量展示，通常以IM(地震动强度参数)为自变量轴，超越概率为因变量。由该曲线可获得结构在给定IM下，结构地震需求反应参数(μD)达到指定破坏状态下的结构抗震能力参数(μC)的超越概率(Pf)，Pf表达式为：

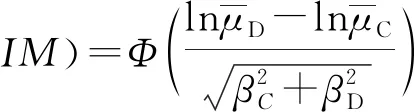
(1)

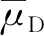
1.1 结构抗震能力参数μc

现行《建筑抗震设计规范》将建筑结构遭遇各种水准的地震影响时，其可能的损坏状况和继续使用的可能性，明确划分成五个地震破坏分级：基本完好、轻微破坏、中等破坏、严重破坏和倒塌[2]。易损性分析时，整体结构的各破坏状态与其最大层间位移角θmax的关系如表1所示。其中，[ue]、[up]分别为弹性和弹塑性层间位移角限值，对于钢框架结构，[ue]、[up]分别取1/250和1/50。

表1 结构不同破坏状态判别准则和框架结构能力限值Tab.1 Criteria for different failure states of structures and capacity limits of frame structures

1.2 结构地震需求参数μD

增量动力分析(IDA)方法中基于对地震的随机性的考虑，合理选用结构所在场地的足够多条地震动，通过对每条地震动记录不断调幅，形成一组不同强度的地震动记录，在这组地震动作用下对结构进行一系列的非线性动力分析。通过非线性动力分析可得任一地震动强度下结构的地震反应作为地震动需求参数μD。分别连接这些离散点(IM,μD)得到IDA曲线，其能够正确反映地震作用下结构的地震响应需求，即地震需求曲线。

2 工程概况及有限元模型

2.1 工程概况

北京市大兴区的一栋钢框架结构民用建筑，共6层，首层为食堂，2层～6层为员工宿舍。首层高4.2m，2层～6层高3.2m，平面布置如图1所示，框架结构构件和截面尺寸见表2。

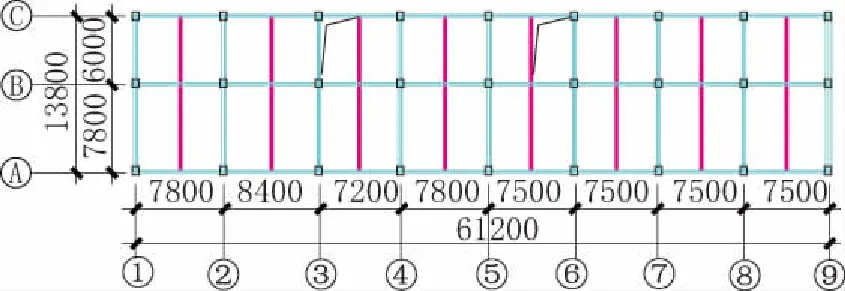
图1 结构平面布置(单位：mm)Fig.1 Plane layout of structure (unit: mm)

表2 纯框架结构梁、柱截面尺寸(单位：mm)Tab.2 Cross section dimensions of beams and columns of pure frame structure (unit: mm)

填充墙均为混凝土空心砌块，砌块强度等级为MU10，砂浆强度为Mb7.5，砌体容重为11.8kN/m3，墙厚取190mm。楼板采用压型钢板组合型楼板，压型钢板型号YX-120-230-690(II), 钢板厚为1.2mm，混凝土板C30，板厚为120mm, 组合楼板通过栓钉等连接件和框架梁相连。建筑场地类别为Ⅱ类，抗震设防烈度8度，设计地震基本加速度值为0.20g，设计地震分组为一组，框架抗震等级为二级。基本风压W0=0.45kN/m2，地面粗糙度为B类。钢材采用Q345B。

利用YJK建模计算，结构满足弹性层间位移角1/250和弹塑性层间位移角1/50的变形控制条件，符合二级框架抗震等级“强柱弱梁”柱梁强度比、强剪弱弯、节点域和长细比、宽厚比等抗震措施要求，保证结构设计的合理性。

2.2 钢框架有限元模型

根据YJK计算设计截面，建立etabs有限元模型，其中楼板以等效荷载形式施加于框架梁，通过离散的塑性铰来考虑结构构件的非线性行为。对于钢结构，需要考虑梁、柱的弯曲变形和剪切变形，梁单元采用主方向的M3铰，柱单元采用P-M2-M3铰。填充墙模拟采用Saneinejad和Hobbs[3]提出的斜撑宽度(w)计算公式确定等效斜撑模型，并在等效斜撑中部布置轴力P铰。

(2)

(3)

式中：H为框架层高；L为框架梁长；λ为相对刚度系数；tw为填充墙厚度；Hin为填充墙的高度；Ec为框架材料的弹性模量；Ew为填充墙材料的弹性模量；Ic为柱正交荷载方向的惯性矩；θ为斜撑与水平梁的夹角。

由于地震作用是往复作用的动荷载，震害中填充墙多表现为交叉斜裂缝。所以用单方向的压杆不能正确反映地震作用下墙框的相互作用，本文在建立地震作用下墙框协同作用计算分析模型时将单对角斜撑转化成双对角斜撑，双对角斜撑中每根压杆的宽度w1均为式(2)计算斜撑宽度w的一半。

图2 等效斜撑本构Fig.2 Equivalent diagonal brace constitutive model

等效斜撑材料采用文献[4]所推荐的应力-应变关系，如图2所示。其中：fm为砌体轴心抗压强度平均值；f1为砌体的抗压强度等级;f2为砂浆的抗压强度等级，f2≥1时k2=1。砌体抗压强度设计值f=0.45fm，砌体抗压强度设计值f及对应的应变εe=f/E作为砌体应力应变曲线的比例极限点，其中砌体弹性模量E根据《砌体结构设计规范》[5]中表3.2.5-1计算。峰值应力下的峰值应变ε0为0.003；残余强度下的极限应变为2ε0，极限压应变取3ε0。等效斜撑具体参数见表3。

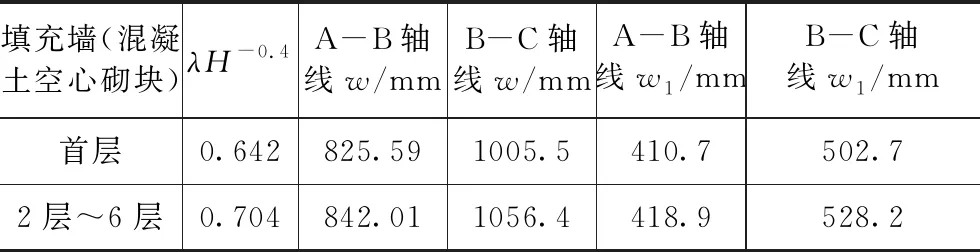
表3 等效斜撑具体参数Tab.3 Specific parameters of equivalent diagonal brace

根据表3填充墙相关参数分别建立底层无墙、中间层无墙及顶层无墙三种空间纯框架结构有限元模型，如图3所示。

图3 不同薄弱层结构Fig.3 Structure of different weak layers

3 钢框架结构地震易损性分析

从PEEK强震数据库中挑选与我国II类场地类似，且满足ATC-63[6]所要求的震级超过6.5、PGA超过200gal的13条强震地震记录，各地震波的加速度反应谱及规范设计反应谱见图4。

图4 各地震记录加速度反应谱及设计反应谱Fig.4 Acceleration response spectrum and design response spectrum of each seismic record

3.1 含薄弱层结构IDA曲线

根据上述13条地震动记录，以最大层间位移角θmax为IM，利用增量动力方法对结构进行非线性动力分析，绘制各结构IDA曲线如图5所示。

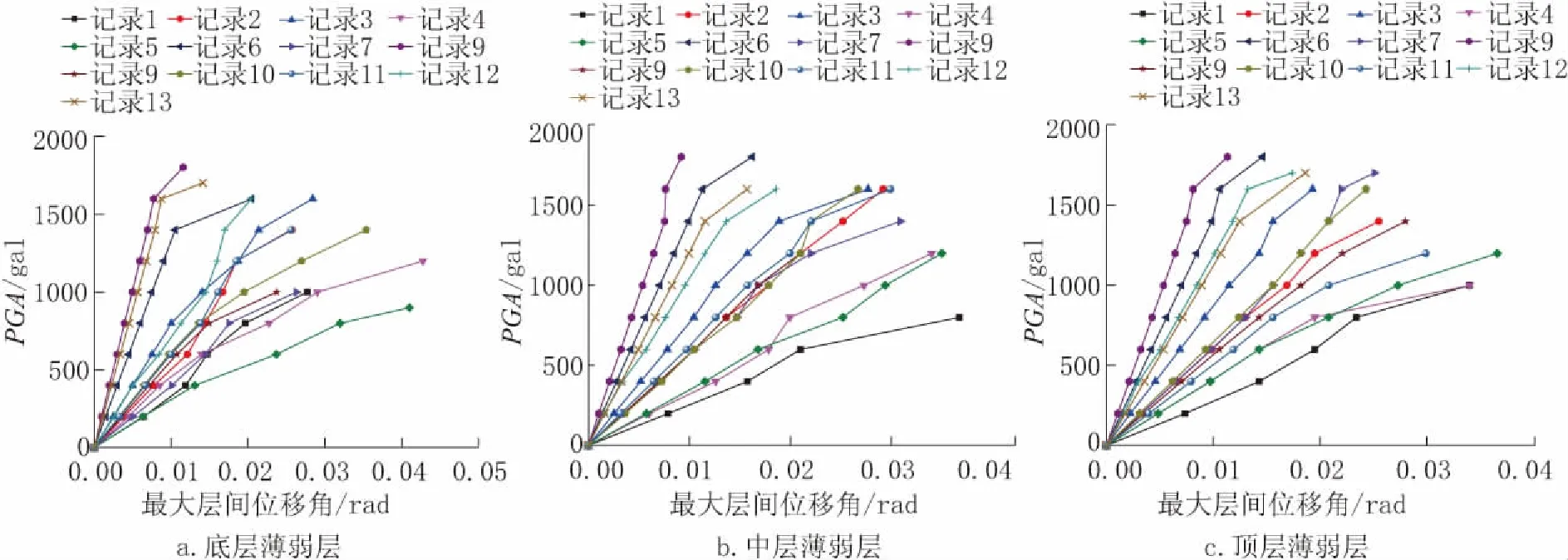
图5 不同结构IDA曲线Fig.5 IDA curve of different structure

可见不同地震记录下IDA曲线离散性较大，对IDA曲线进行概率统计，得到50%分位线位概率需求曲线如图6所示。

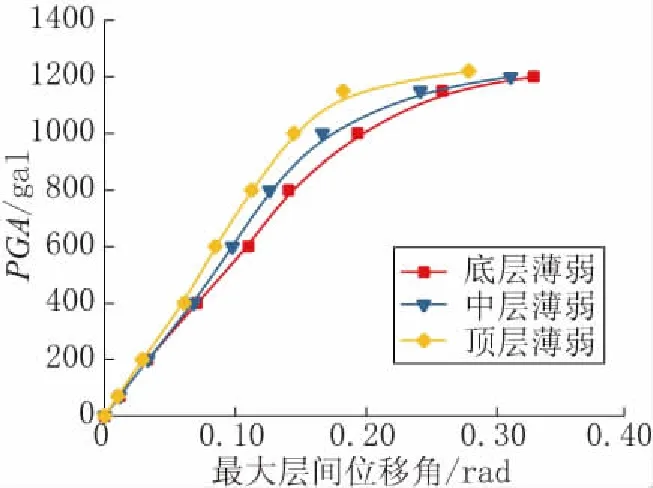
图6 不同薄弱层结构地震需求曲线Fig.6 Seismic demand curve of structures with different weak layers

由图6可见不同结构初始均存在线弹性阶段，随着地震动的增大逐渐进入平缓阶段。其中底层为薄弱层结构在PGA为1150gal时进入水平段，最大层间位移角为2.75%；中层为薄弱层结构在PGA为1150gal时进入水平段，最大层间位移角为2.5%；顶层为薄弱层结构PGA为1200gal时进入到平缓阶段，对应最大层间位移角为1.8%。由此可见底层为薄弱层对结构承载能力及延性的影响最大。

3.2 含薄弱层结构易损性曲线

以50%分位线为地震需求曲线[7]，根据式(2)、式(3)，计算得各含薄弱层结构不同破坏状态下的超越概率，绘制易损性曲线如图7所示,图中自下而上不同颜色分别代表结构倒塌、严重破坏、中等破坏、轻微破坏几种状态。

由图7可见不同薄弱层结构的地震易损性有明显的差异，其中底层为薄弱层结构各破坏状态的超越概率最高，中层为薄弱层结构次之，顶层为薄弱层的结构地震各破坏状态的超越概率最低。由此可知底层为薄弱层对结构地震易损性影响最大，中层为薄弱层次之，顶层为薄弱层对结构地震易损性影响最小。

图7 易损性曲线对比Fig.7 Comparison of vulnerability curve

3.3 含薄弱层结构破坏概率矩阵

对于8度设防地区，各地震作用水平地震影响系数最大值amax及加速度峰值[8]如表4所示。

表4 8度设防地区地震作用水平相关参数Tab.4 Relevant parameters of seismic action level in 8-degree fortification area

结构基本完好的概率等于1减去轻微破坏的超越概率；发生轻微破坏的概率等于轻微破坏的超越概率减去中等破坏的超越概率；发生中等破坏的概率等于中等破坏的超越概率减去严重破坏的超越概率；发生严重破坏的概率等于严重破坏的超越概率减去倒塌的超越概率；发生倒塌的概率即为倒塌的超越概率。由易损性曲线可得到8度区不同薄弱层结构在不同PGA下的破坏概率。

为统计方便，基本完好、轻微破坏、中等破坏、严重破坏、倒塌五种状态分别对应于BI、SD、MD、CD、ED。由此可得PGA为70gal、200gal、400gal、1000gal各结构破坏概率柱状图，如图8所示。

图8 不同PGA下结构破坏概率分布Fig.8 Probability distribution of structural failure under different PGA

由图8可知，小震下薄弱层对结构的影响较小，随着地震动增强影响作用明显增强。大震下，

底层薄弱中等破坏、严重破坏、倒塌的概率均比中层薄弱及顶层薄弱结构高，表明在同一PGA下底层薄弱结构破坏最为严重，中层薄弱次之，顶层薄弱对结构影响最小。当PGA达到1000gal时，底层薄弱结构倒塌状态概率明显高于中层薄弱及顶层薄弱结构，破坏概率分别为47.4%、25.7%、25.8%，表明强震下，底层薄弱结构最容易发生倒塌破坏，此时应考虑结构底层加强。

4 结构破坏模式及塑性发展过程

4.1 含薄弱层结构破坏模式

为探究不同薄弱层结构的破坏过程，选取延性较好的地震记录1为研究对象，可得不同设防地震下结构各层间位移角分布情况，如图9所示。

由图9a可见底层薄弱结构在小震、中震、大震下结构最大层间位移角均位于第一层，随着楼层的增高，层间位移角逐渐减小。

由图9b可见，中层薄弱结构在小震、中震、大震下结构最大层间位移角位于第四层，即结构薄弱层。并且通过层间位移角分布曲线可知，随着地震动的加强，最大层间位移角与其他层层间位移角差值越来越大。

由图9c可见，顶层薄弱结构在小震、中震、大震下结构最大层间位移角位于第二层，虽然第六层层间位移角大于第五层层间位移角，但其并不是结构最大层间位移角位于层。

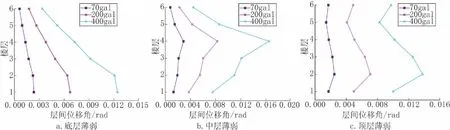
图9 不同设防地震下结构各层位移角Fig.9 Displacement angle of each layer of structure under different fortification earthquakes

综上所述可见，对于底层薄弱及中层薄弱结构，最大层间位移角均位于薄弱层。而对于顶层薄弱结构最大层间位移角位于结构第二层，这与无薄弱层最大层间位移角位于楼层相同；表明对于底层薄弱及中层薄弱结构，因薄弱层的存在，结构的破坏模式改变，结构薄弱层将先于其他层破坏。对于顶层薄弱结构，虽然顶层位移角有所改变，但并不影响结构的破坏模式。

4.2 含薄弱层结构塑性发展过程

为更进一步探究结构破坏机理，取地震记录1下PGA为1000gal不同薄弱层结构塑性发展终态损伤最为严重一榀框架塑性铰状态图，如图10所示。

图10 不同薄弱层结构塑性发展过程Fig.10 plastic development process of structures with different weak layers

由图10a可知，1000gal终态下，底层薄弱结构首层及第二层柱塑性铰首先失效，上部结构填充墙也基本达到完全破坏状态，梁端塑性铰发展充分。

由图10b可知，1000gal终态下，中层薄弱结构柱两端塑性铰达到失效状态，薄弱层梁端塑性铰也发展较充分，薄弱层相邻填充墙塑性铰基本均达到承载极限状态，而这时首层柱并未进入到塑性状态。

由图10c可知，1000gal终态下，顶层薄弱结构首层柱两端塑性铰首先达到承载极限状态，上部结构塑性铰为发展初期，顶层梁柱都未进入塑性状态。

综上所述，可见底层薄弱及中层薄弱均会改变结构的破坏模式，顶层薄弱对结构破坏模式无影响。并且底层薄弱结构墙、梁、柱塑性发展最为充分，多处构件塑性铰已达到失效状态，这种工况最为不利，在结构设计中应尽量避免或对薄弱层采取加固处理。

5 结论

本文基于易损性分析理论，对因填充墙布置导致的不同情形薄弱层结构进行了地震易损性分析并探究了不同薄弱层结构的破坏机理，以期为结构抗震及加固设计提供一定参考，结论如下：

1.由结构地震易损性曲线可知，不同位置薄弱层对结构有不同程度的影响，底层薄弱对结构影响最大，中层薄弱次之，顶层薄弱对结构影响最小。

2.由地震破坏概率柱状图可知，底层薄弱对结构危害最大，此结构破坏最严重，最易发生倒塌。且随着地震动的加强，不同薄弱层对结构抗震性能的影响差异越来越显著。

3.通过对比楼层层间位移角及各结构塑性发展过程可知，底层薄弱及中层薄弱结构最先在薄弱层发生破坏，并改变结构的破坏机制。顶层薄弱对结构破坏模式无影响。