基于位移反分析法的边坡失稳计算

宋宝宏

(北京市市政工程设计研究总院有限公司 100082)

引言

边坡的稳定是暂时的、相对的，即便是现在稳定的边坡，在经过长期的地质作用或人类活动等不利因素影响，可能由稳定状态向不稳定状态发展，最终造成边坡失稳[1]，造成极大的人员伤亡。因此，深入开展边坡的稳定性分析具有重要的理论意义及深远的现实意义。许多专家学者，在边坡失稳机理、表现形式、预警方法、治理手段等方面进行了大量的研究，并且取得了丰硕的成果。如经典的极限平衡方法[2]是通过潜在滑体的受力分析，引入摩尔-库仑强度准则，得到了广泛应用。蠕动理论[3]采用了物理模拟和数值模拟方法，总结归纳出了常见的边坡变形破坏形式。位移反分析思路最初由Kavanagh和Clough[4]于1971年提出，其原理是基于实际工程的位移数据采用数值分析软件反演出岩体部分参数，如H.A.D.Kirsten[5]利用现场工程实测变形量反分析岩体弹性模量，徐文文[6]针对露天矿山地质条件复杂，采用BP网络获得位移与内部地质力学参数之间的关系。

本文通过借助位移反分析的思路，在已知岩体弹性模量等地质参数的条件下，以某矿山露采高边坡作为研究对象，借助实时监测系统得到的边坡位移数据，通过直接施加位移的方法，来反推边坡的稳定性，建立位移与安全系数之间的非线性关系，从而预测边坡失稳的位移量，并为类似高边坡失稳预测和预警方法提供研究思路。

1 三维模型建立

1.1 工程概况

图1 监测边坡现状Fig.1 The real of the slope

某矿为露天开采的多金属矿，经过多年开采，目前形成的露采边坡最大高度为286m，平均高度超过200m，现况如图1所示。由于坡体高度较高，且所在区域降水量大，故建立起雷达监测预警体系，对坡体重点区域的表面位移进行实时监测。监测系统水平角度为60°，俯仰角度为30°，监测区域如图2所示。

监测系统布置于露采边坡对面的观测房中，距离所监测边坡最近直线距离约为700m。该系统通过雷达发射电磁波，并采用干涉差分技术，以雷达为原点，来获得边坡变化的相对位移，可实时获得监测范围内任意位置的位移变化数据，在监测界面上选取不同的点，便可得到不同位置的位移变化值。

如图2所示，不同颜色区域表示不同的位移变化情况。当位移变化速率达到预定预警值时，系统会发生预警，在试运行过程中，预警值随实际情况进行调整。

图2 雷达监测区域Fig.2 The area of radar observation

1.2 模型建立

FLAC3D采用显式拉格朗日算法和混合-离散分区技术，能够非常准确地模拟材料的塑性破坏和流动，ANSYS在建立复杂模型上具有明显的优势。本次计算模型首先在ANSYS中建立，并划分网格，再导入FLAC3D中进行计算，选择摩尔-库仑模型进行分析。在ANSYS中建立的模型如图3所示，导入FLAC3D中如图4所示。考虑到露采边坡范围较大，本次建模仅选取边坡雷达监测范围内区域。

图3 露采边坡ANSYS模型Fig.3 The side-slope model of ANSYS

图4 露采边坡FLAC3D模型Fig.4 The side-slope model of FLAC3D

实际边坡为矿山露采边坡，坡体脚部较为平缓，不在监测范围内，顶部台阶较小，建模中对坡体进行适当简化。所建模型整体长约572m(Y向)，宽约403m(X向)，高约215m(Z向)。其边界条件设置为：固定模型底面X、Y、Z方向位移及速度，固定Y轴侧面的Y向位移及速度，固定模型后表面的X向位移及速度。

2 正向稳定性分析

计算模型力学参数根据地质资料选取，具体各项参数如表1所示，计算方法采取强度折减法。

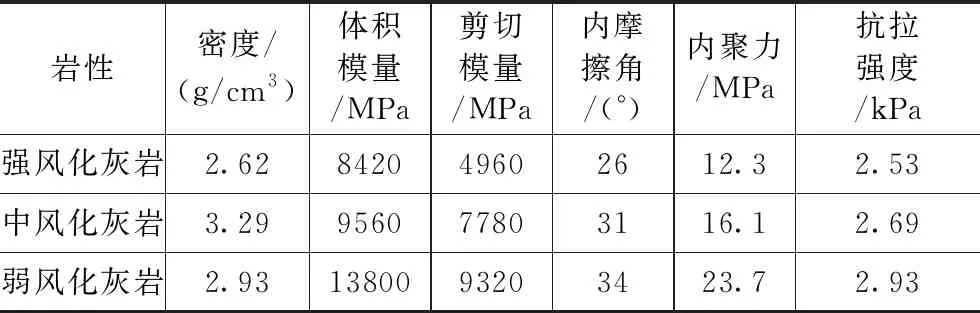
表1 自然状态下岩土体力学计算参数Tab.1 Calculation parameters of rock and soil in natural state

强度折减法可有效获得边坡安全系数，基本原理为：通过对边坡岩土体主要物理力学参数(如内聚力、内摩擦角、弹性模量等)进行折减，从而得到边坡临界破坏时的折减系数，折减系数为岩土体的实际抗剪强度与折减后的临界破坏时抗剪强度之间的比值，该折减系数即为安全系数。

如果用c和φ分别表示岩土体的真实粘聚力和内摩擦角，用F表示安全系数(抗剪强度比值),则式(1)和式(2)表示了整个折减过程，通过两式的反复折减计算，即可得到相应的安全系数。本文即采用粘聚力和内摩擦角的折减来获得安全系数。

cF=c/Ftrial

(1)

φF=tan-1[(tanφ)/Ftrial]

(2)

式中：cF为折减后的粘结力；φF为折减后的摩擦角；Ftrial为折减系数。

对模型赋予力学参数后，先设置弹性本构模型， 建立未开挖的原始模型，求得原始的地应力场，通过模拟开挖，在此卸荷过程中得到的最终位移值清零，以对应监测位移值。再设置成摩尔-库仑模型，进行边坡稳定性安全系数计算。具体折减过程中塑性区分布情况如图5所示。

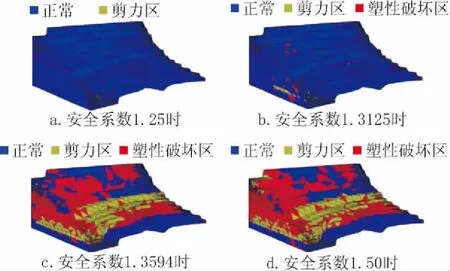
图5 折减过程中的塑性区分布Fig.5 Distribution of plastic regions during reduction

从图5中可以看出，左侧坡脚最先产生塑性区，坡顶也有很小一部分塑性区，随着折减的增加，塑性区逐渐增加，向坡顶及坡体中部发展，中部主要表现为剪切破坏，及部分受拉破坏，坡体上部表现为受拉破坏。由边坡破坏性准则中的滑动带塑性区贯通准则可得，当抗剪强度折减系数达到1.3516时，边坡塑性区基本贯通，此时边坡可能产生不断发展的变形和位移，因此求得边坡的安全系数是1.3516。

3 反位移分析

反分析法是以能反应系统内部力学行为变化的、可测量的物理量作为基础，通过一定的系统模型，反演推出系统内部的目标物理量，该物理量可以是力学参数、初始地应力、位移变化等。作为岩土工程反分析的一部分，位移反分析法即是以可观测的位移数据作为待反演的对象，来判断边坡的稳定性。

本节以雷达监测得到的位移数据作为基础，根据1.2节所建立的边坡三维数值分析模型，反算不同位移变化量下边坡的稳定性。从而得到位移变化量与安全系数之间的关系，并计算出边坡破坏时可能的位移临界点，作为预警阈值的参考。

3.1 反分析计算原理

边坡位移变化受内外多种因素的共同影响，情况较为复杂，因素包括降雨、震动、坡体岩土力学参数、时间等，理论上可用式(3)表示。

S=f(E、c、φ、υ、D、T、Q、…)

(3)

式中:S为位移;E为弹性模量;c为内聚力;D为抗拉强度;φ为内摩擦角;T为时间;Q为降雨量。

边坡位移的变化大小最终又反映在边坡的稳定性上。且由于在实际工程中诸多影响因素相互作用，很难判断其间具体的相互关系，而位移数据便于获取，所以可建立位移与安全系数之间的关系，故可将式(3)进行简化，如式(4)所示，其中F代表安全系数。

F=S(E、c、φ、υ、…)

(4)

当以位移变化作为边坡稳定性反分析的基础后，即可反演出边坡稳定性的变化，从而判断边坡破坏临界点的位移值。这就是位移反分析的本质。

由于实际边坡监测表面各点位移大小有所差别，为了便于计算，以及尽可能模拟实际效果，本次模拟对位移荷载大小及范围进行适当简化，即施加荷载范围为观测区域整体，大小一致。

本文选取图2中15个点的30天累计位移数据进行分析，如表2所示。

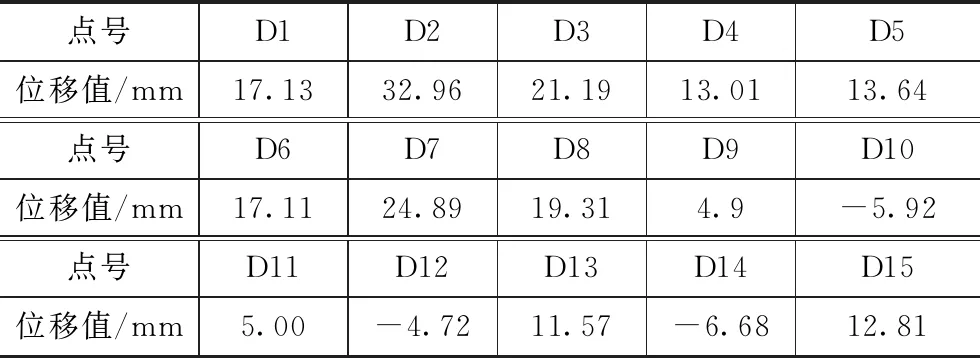
表2 各点监测位移值Tab.2 Monitored displacement

从表2中可知D1至D15各点位移累积变化值相差并不大，得到监测区域的位移累积30天变化平均值约为11.75mm。

由于FLAC3D计算时的迭代时步不能等效于真实时间，所以无法获得一定时间间隔内的位移变化量，且受软件自身限制，其位移荷载不能直接施加于模型上，需要换算为速度荷载与迭代步数乘积，且速度荷载要尽量小，迭代步数尽量多，这样才能尽可能得到准确结果[7]。如需模拟位移变形量为1cm，可设置成施加大小为1×e-6m/s的速度荷载，迭代10000步即可。

3.2 计算结果及分析

本节在计算过程中，速度荷载基值先取为1×e-6m/s。结合实际建模大小，施加范围为5≤x≤398、1≤y≤597、24≤z≤214，施加效果如图6所示。

图6 基值速度荷载下X方向位移云图(单位：m)Fig.6 The vertical X-displacement contours under the velocity load of 1m/s(unit:m)

根据不同的位移变化量，设置相应的迭代步数，判断不同大小位移载荷下边坡的稳定性。将监测系统得到的区域内位移累积30天变化平均值作为第一组荷载数据，并递进增加,直到边坡破坏为止。本次计算载荷最大值暂取为50mm，共分为13组，具体施加的位移载荷取值如表3所示。

表3 施加的位移荷载Tab.3 Applied displacement load

对表3各组位移荷载进行计算，得到位移变化量如图7所示。由于组数较多，在此仅给出其中的6组图。

图7 X方向位移云图(单位:m)Fig.7 X-displacement nephogram(unit:m)

由图7可知，计算完成后，坡体整体X向位移大小等于施加的位移载荷大小，在局部有所变化，其中坡体左上角部分区域(+96平台至+215平台左侧)会有所增大，增大量约为10mm至30mm不等，上部中间区域会有所减小，减小量30mm至50mm不等。由于表体位移荷载的施加，坡体内部位移也相应增大，大体与表体位移相等，靠近内部边界区域位移相应减小，趋于零。这是由于其他边界对位移进行了约束。

得到安全系数与位移之间的关系如表4所示。

表4 不同位移荷载下的安全系数Tab.4 Safety factor under different displacement loads

根据以上计算结果，建立安全系数与位移值之间的关系，如图8所示。

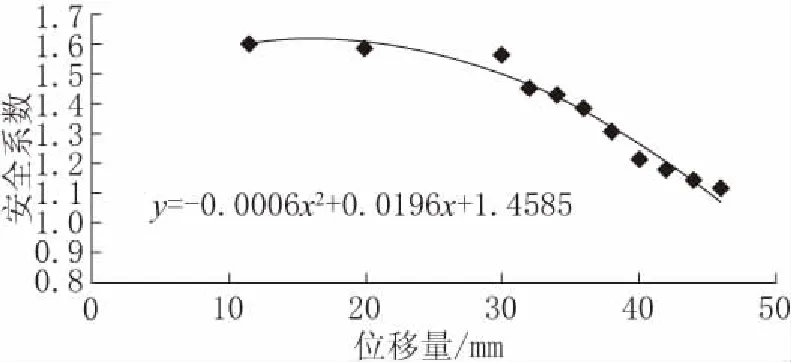
图8 安全系数与位移量关系曲线Fig.8 The relationship between the safety factor and displacement

令y为安全系数，x为位移荷载大小，对其进行二次函数拟合，得到的函数为y=-0.0006x2+0.0196x+1.4585。若安全系数为1.15时，计算出位移荷载为44.28mm，当然这只是一个累积位移变化量。相对来讲，边坡破坏以位移变形速率作为参考值更为准确，但位移量的变化也反应了边坡的形变情况，尤其对于本文所探讨露采边坡为多金属矿露采边坡，通常边坡较为稳定，如发生较大的位移，也能反映出边坡稳定性受到了破坏。

同时，根据以上结果，也可以看到位移形变小于30mm时，安全系数的减幅较为缓慢，当位移大于30mm时，安全系数迅速减小。当位移量达到48mm时，安全系数接近1，通常来讲，安全系数在接近1时即可发生破坏，1.15以上的安全系数才能确保边坡稳定性。所以在实际工程中如发现一段时间边坡位移量达到或超过44mm左右时，边坡的稳定性即很有可能发生破坏。

4 结论

本文基于实际矿山露采边坡，通过数值计算软件建立计算模型，从正反两个方向对边坡稳定性进行分析，并通过反向位移分析对边坡失稳破坏可能的临界点进行了预测，可得到以下结论：

1.通过三维数值建模，正向计算了边坡的整体稳定性，分析了其应力状况及塑性区分布，得到安全系数为1.3516，进一步证明了边坡此时的稳定性。

2.位移的反分析则通过给边坡表体施加位移荷载，再采用强度折减法进行计算，得到边坡稳定性与位移荷载大小之间的非线性关系，拟合得到函数关系，获得边坡破坏时位移荷载的大小及边坡临界破坏时可能的位移变形量，为可能的破坏临界点做出预测。

此外，本文选定的位移平均值为15个点的平均值，不能很好地展现各区域的位移变化情况，且选取的点也可能受到现场开采的影响，固后续的分析可对此做出优化。

综上所述，本文的研究，尤其正反分析的方法，可作为相关研究思路，为工程实际应用提供参考，但仍存在一些不足。在位移荷载的模拟上，应考虑降雨、地质力学参数、爆破震动共同作用下的影响，进一步优化荷载加载的真实性，也应进一步探讨速率加载的影响。