经典人工智能算法综述

摘 要：人工智能算法繁多，但经得起实践考验的经典算法有限，常见的有朴素贝叶斯、决策树、逻辑回归、支持向量机、深度学习、强化学习、遗传算法、蚁群算法、元学习等。依据人工智能算法理论基础知识，如概率统计、集合论、空间几何、图论、矩阵论等加以分类，并对相应经典人工智能算法概念和主要应用领域进行概述，去除结构细化和公式展开所带来的复杂感，揭开人工智能的神秘面纱，让算法整体轮廓得以更清晰地呈现。

关键词：人工智能算法;朴素贝叶斯;逻辑回归;深度学习;遗传算法

DOI：10. 11907/rjdk. 191702

中图分类号：TP3-0    文献标识码：A                文章编号：1672-7800（2020）003-0276-05

Overview of Classical Artificial Intelligence Algorithms

TAO Yang-ming

（School of Computer and Information Engineering， Nanning Normal University， Nanning 530023，China）

Abstract： The artificial intelligence algorithm has a great variety. However， the classical algorithms that can withstand practice and test are actually limited. At present， classical artificial intelligence algorithms include naive Bayes， decision tree， logistic regression， support vector machine， deep learning， reinforcement learning， genetic algorithm， ant colony algorithm， and meta-learning. The paper classifies the main theoretical basic knowledge of artificial intelligence algorithm such as mathematical probability and statistics， set theory， space geometry， graph theory， matrix theory， etc， and summarizes the classical artificial intelligence algorithm concept and main application fields of corresponding classification， and removes the structure. The refinement and formula unfolding brings a sense of complexity to beginners， uncovering the mystery of artificial intelligence， and allowing beginners to have a clear understanding of the overall outline of the algorithm.

Key Words： artificial intelligence algorithm; naive Bayes; logistic regression; deep learning; genetic algorithm

0 引言

人工智能算法起步于20世紀50年代，经过不断发展，其种类已颇为繁多，然而经得起实践考验的经典算法仍很有限。目前，有依据算法结构分类的，如迭代、递归、贪心算法、动态策划、分治策略等;有依据应用分类的，如回归算法、分类算法、模式识别算法等;还有一些并没有严格分类，只是就几种大型方法进行总结和算法展开。人工智能算法通常比较复杂，依据上述分类基本上会面临结构细化、公式代入、各种引用等，这些内容一经展开无疑十分庞杂。实际上，每种人工智能算法所依据的概念很简单，而且很多经典库如Python中的Gensim、TensorFlow、Scikit-Learn等都对一些常用的人工智能算法进行了封装，初学者可在了解算法基本概念后直接对这些封装的库进行使用和实验。值得注意的是，就应用而言，本文可以帮助初学者迅速理解算法精要并使用现有算法库;就研究而言，想要创新算法乃至开发自己独有的算法，结构细化和公式的深入理解必不可少。

1 基于集合论分类

集合论是数学学科的根基，初等数学方法有加减乘除等各种运算、映射、函数、导数等概念，高等数学有极限、积分、微分、级数等概念。基于集合论的经典人工智能算法有K-means（K均值算法）、k-NN（k近邻算法）、Apriori算法等。

1.1 K-means算法

K-means（K均值算法）[1]是非监督学习中的经典聚类算法，主要基于“物以类聚，人以群分”概念，将未标注的样本数据中的相似部分聚集为同一类。实现流程为：①随机选取k个对象作为初始聚类中心;②计算每个对象与各聚类中心的距离，并将每个对象分给距离它最近的聚类中心;③重新计算聚类中心，然后重复②，直至满足终止条件，终止条件可以为没有对象再分给聚类中心，也可以为聚类中心的误差平方和局部最小等。

极大似然估计在规律分布数据集中表现良好，对于含隐藏变量的数据集表现较差。鉴于此，最大期望值算法在极大似然估计中加入隐藏变量，实现步骤是：①利用隐藏变量计算出初始期望值;②使用期望值对模型进行最大似然估计;③使用②得到参数代入①重新计算期望值，重复②，直至得到最大期望值。

最大期望值算法主要运用于参数求解和优化，尤其是在机器学习领域有广泛应用。

2.6 PageRank算法

PageRank算法[9]是Google专有算法，也称网页排名或佩奇算法。PageRank的理念十分简单，即如果一个页面被越多的其它网页引用，其等级也越高;如果一个等级高的页面引用了一个等级低的页面，则该等级低的页面等级会有所提升。

PageRank算法主要应用于网页排名。

3 基于图论分类

图分为有向图、无向图、带权图、连通图、平面图等传统图结构，以及欧拉图和哈密顿图等一些特殊结构的图。树结构也是图的一种，可以视为非连通图。基于图论的人工智能算法有决策树、Adaboost、Bagging等。

3.1 决策树

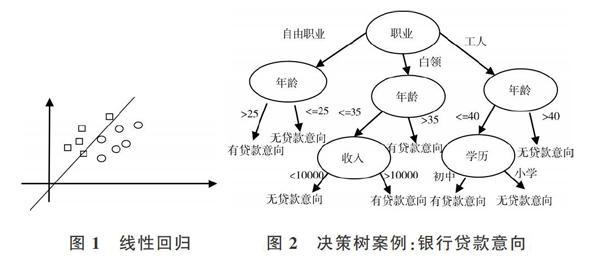
决策树（Decision Tree）[10]是和朴素贝叶斯一样的经典且使用广泛的分类算法，最初使用ID3算法生成决策树，后来在ID3的基础上延伸出C4.5算法和CART算法。决策树的构造步骤非常简单：①生成整体决策树框架;②修剪决策树。相关案例如图2所示。

决策树主要应用于分类，基本上朴素贝叶斯能运用的领域，决策树也能，如文本分类、新闻分类、病人分类等。

3.2 随机森林

随机森林（RandomForest）[11]由多个决策树构成，决策树是对整个数据集进行构建，而随机森林先利用Bagging方法在初始数据集进行随机抽样并生成多个子数据集后，再分别对子数据集进行决策树构建。需要注意的是，子数据集的数据量必须与初始数据集的数据量相同，如图3所示。

随机森林主要解决决策树泛化能力弱的缺点，可以理解为“三个臭皮匠顶个诸葛亮”的概念，与决策树一样，主要应用领域是分类。

4 基于空间几何分类

空间集合的概念主要是维度，如一维的线条、二维的平面、三维的立体空间、四维及以上的超空间等;再者是向量，通过向量之间的计算可以快速计算出样本特征各种联系、提取关键特征等。基于空间几何的人工智能算法有支持向量机、空间向量模型等。

4.1 支持向量机

支持向量机（Support Vector Machines，SVM）[12]主要有3类：线性可分SVM，线性不可分SVM和非线性SVM。线性可分SVM指在二维平面内可以用一条线清晰分开两个数据集;线性不可分SVM指在二维平面内用一条线分开两个数据集时会出现误判点;非线性SVM指用一条线分开两个数据集时会出现大量誤判点，此时需要采取非线性映射将二维平面扩展为三维立体，然后寻找一个平面清晰的切开数据集。

在实际应用中，SVM不仅用于二分类，也可用于多分类。SVM在垃圾邮件处理、图像特征提取及分类、空气质量预测等多方面领域都有应用。

4.2 向量空间模型

向量空间模型（Vector Space Model，VSM）[13]主要应用于自然语言处理领域的文本特征提取，如图4所示。

有3个文档D1、D2、Q，D1和D2均含T1、T2、T3特征项，Q只含T2特征项，特征项可以理解为对文档抽取的关键词。D1=2T1+3T2+5T3的（2，3，5）表示T1、T2、T3在文档D1中的权重，同理（3，7，1）表示T1、T2、T3在文档D2中的权重。如果要计算D1和D2相似度，则直接计算（2，3，5）和（3，7，1）的余弦值即可。

5 基于交叉学科分类

目前，很多人工智能算法是基于交叉学科的，如通过模拟人类神经网络的深度学习算法、基于“物竞天择适者生存”进化论概念的遗传算法、通过观察蚁群活动而产生的蚁群算法等。

5.1 深度学习（神经网络）

深度学习的“深度”二字源于神经网络隐藏层的层数可以人为增加，即整个算法的长度会不断增加。神经网络算法近几年给整个计算机领域带来了革新，同时也影响了其它学科，甚至对整个社会也产生了深远影响。

神经网络算法总给人一种神秘莫测的感觉，让人望而生畏，其实神经网络本质很简单，大概经历了3个阶段：①简易线性前向传播，此时的神经网络有另外一个名字叫“多层感知机”[14]，神经元的运算本质即为简单的矩阵相乘而已;②非线性反向传播，就是在多层感知机的基础上加入偏置和激活函数让线性转化为非线性，利用损失函数和梯度下降算法转变前向传播为反向传播，通过反向传播不断改进参数最终使损失函数值达到预期，第二阶段后期又出现多种优化算法如学习率可以改变梯度下降算法的幅度、正则化解决过拟合问题、滑动平均算法使模型更健壮等，第二阶段的神经网络称为“人工神经网络”[15]或者“全连接网络”;③神经网络进化阶段，在人工神经网络的基础上衍生出能够权值共享的卷积神经网络（CNN）[16]、解决序列问题的循环神经网络（RNN）[17]、在RNN上改进的LSTM以及其它一些递归神经网络、生成式对抗网络（GAN）、脉冲神经网络（SNN）等，同时也衍生出一些基于神经网络的经典模型如bi-LSTM、bert模型等。

神经网络目前已经得到了广泛应用，人脸识别、机器翻译、文本分类、无人驾驶等。神经网络在应用领域几乎是万能的，以至于好多科研人员已经得出“神经网络之后再无智能算法”的结论。

虽然神经网络算法如此强大，但目前仍有两大问题无法解决：一是可以使用神经网络得出想要的结果，但为何会得出这样的结果始终无法破解，现在还没有这方面的理论能够说服大家，也即神经网络的内部是个黑盒，能够拿来用并且得出不错的结果，可是“知其然不知其所以然”;二是神经网络根基的反向传播算法目前都受到质疑，尤其作为神经网络之父的Hinton设计了Capsule算法代替反向传播算法，之后又有研究者提出离散优化等方法取代反向传播算法。

5.2 遗传算法

遗传算法[18]是模拟人类和生物的遗传—进化机制，主要基于达尔文的生物进化论：物竞天择、适者生存和优胜劣汰。具体实现流程是：①从初代群体里选出比较适应环境且表现良好的个体;②利用遗传算子对筛选后的个体进行组合交叉和变异，然后生成第二代群体;③从第二代群体中选出环境适应度良好的个体进行组合交叉和变异形成第三代群体，如此不断进化，直至产生末代种群即问题的近似最优解。

遗传算法通常应用于路径搜索问题，如迷宫寻路问题、8字码问题等。

5.3 蚁群算法

蚁群算法[19]的灵感来源于观察蚂蚁集体觅食行为的现象，单个蚂蚁在觅食过程中會在路径中遗留下“信息素”，蚂蚁都具备判别“信息素”浓度的本能，如果在某条路径上有高浓度的“信息素”即可判定为该路径是最佳觅食路径。实现流程同样类似：①初始化参数，构建整体路径框架;②随机将预先设定好的蚂蚁数量放置在不同的出发点，记录每个蚂蚁走的路径，并在路径中释放信息素;③更新信息素浓度，判定是否达到最大迭代次数，若否，重复第二步，若是则结束程序，输出信息浓度最大的路径即为获取的最佳路径。

蚁群算法和遗传算法类似，主要用于寻找最佳路径，尤其在旅行商问题（TSP）上被广泛采纳。

5.4 退火算法

退火的概念来源于物理学科热力学，指要得到固体的理想有序结晶状态，需要先加温加快固体内部的分子运动，再缓慢降温降低分子运动，直至得到规则有序的结晶状态;不可快速降温，过快的降温是无法得到理想结晶状态的。如图5所示。

退火算法（Simulated Annealing）[20]和爬山算法（Hill Climbing ）有些类似，都属于贪心算法。爬山算法的缺点是只能得到局部最优解，退火算法由于加入了随机因素，所以在找到局部最优解后会跳出来继续寻找，直至找到全局最优解。

退火算法在寻找最优解中被广泛使用，如优化车间调度流程、旅行商问题等。

5.5 强化学习、迁移学习和元学习

强化学习（Reinforcement Learning）[21]，也叫评价学习或再励学习。强化学习的算法概念基于心理学的行为主义理论，即在一定环境中给有机体奖励或者惩罚，能够刺激有机体养成利益最大化的惯性行为。强化学习本质上是一种算法思想，需要同其它算法结合使用，比如结合神经网络算法。

迁移学习（Transfer Learning）[22]的本质可以浓缩为“举一反三”，此概念可以追溯到1901年的心理学家桑代克和伍德沃思，主要思想是将某个领域获取的经验、知识迁移到另外一个领域的学习中。需要注意的是，迁移学习和预训练方法有本质不同，迁移学习针对的是两个不同的数据集，预训练方法是在原有数据集的基础上添加新数据。

元学习（Meta Learning），也称之为学会学习（Learning to Learn）。元学习的概念很简单，就是利用以往学过的知识和经验能够自主学习并培养出新技能。由于传统机器学习都需要靠给机器喂大量的数据才能让机器具备一定的智能，因此元学习概念的提出是革命性的。目前，元学习相关研究处于“百家争鸣”的状态，有基于记忆方法、基于预测梯度方法、基于注意力机制等。

6 常见特征提取及优化方法

现实生活中的文本、图像、语音等需要被转化为二进制数据才能被计算机识别，因此需要对这些原始材料进行数据转化，该过程被称为特征提取。特征提取方法层出不穷，在特征提取过程中，涌现出了很多优化方法，使得特征提取更快、更有效。

6.1 特征提取方法

提取图像特征最常用的方法就是二维矩阵转化，很多工具都可以方便实现，如MATLAB、Numpy等。灰度图片被提取为一个通道的二维矩阵，彩色图片被提取为3个通道（RGB）的二维矩阵。

提取文本的方法非常多样化，有基于统计方法的词集模型和词袋模型，有基于独热编码的独热模型，有基于熵概念的信息增益方法，有基于神经网络的词向量模型等。目前，词向量模型效果最好，基本上自然语言处理领域具备一定智能的模型或者系统都绕不开词向量模型。

6.2 优化方法

通过特征提取方法得到的数据集经常会面临一些问题，比如维度过大、特征稀疏且分散等。因此，需要一些优化方法对得到的数据集进行优化，用于降维的常用方法有奇异值分解（SVD）和主成分分析（PCA），常用的关键特征提取方法有注意力机制等。

7 结语

本文对经典人工智能算法进行了概述，并介绍了每种算法的应用领域和实际应用案例。人工智能算法所基于的理念和概念其实非常简单，但要实现这些理念和概念就绕不开繁琐的数学公式和复杂的算法结构。本文简明扼要地直击每种算法的要义，去除繁琐的公式和复杂的算法结构设计，让初学者快速把握算法整体轮廓，并且在最短时间内通过MATLAB、Gensim、Scikit-Learn等库直接对实际案例进行操作。最后，介绍了数据集的特征提取和优化方法，让初学者对人工智能算法的数据集来源有最基本的认识。

参考文献：

[1]KANUNGO T， MOUNT D M， NETANYAHU N S， et al. An efficient K-means clustering algorithm：analysis and implementation[J].  IEEE Transactions on Pattern Analysis & Machine Intelligence，2002，24（7）：881-892.

[2]ZOUHAL L M， DENOEUX T. An evidence-theoretic k-NN rule with parameter optimization[J].  IEEE Transactions on Systems Man & Cybernetics Part C Applications & Reviews，1998，28（2）：263-271.

[3]陆丽娜，陈亚萍，魏恒义，等. 挖掘关联规则中Apriori算法的研究[J]. 小型微型计算机系统， 2000，21（9）：940-943.

[4]王国才. 朴素贝叶斯分类器的研究与应用[D]. 重庆：重庆交通大学，2010.

[5]李荣陆，王建会，陈晓云，等. 使用最大熵模型进行中文文本分类[J]. 计算机研究与发展，2005，42（1）：94-101.

[6]杜世平. 隐马尔可夫模型的原理及其应用[D]. 成都：四川大学， 2004.

[7]魏大成，周贤刚. 影响综合康复治疗神经根型颈椎病疗效的危险因素逻辑回归分析[J]. 中国康复医学杂志，2009，24（9）：807-809.

[8]基于极大似然准则和最大期望算法的自适应UKF算法[J]. 自动化学报，2012，38（7）：1200-1210.

[9]李稚楹，杨武，谢治军. PageRank算法研究综述[J]. 计算机科学， 2011（b10）：185-188.

[10]杨静，张楠男，李建，等. 决策树算法的研究与应用[J]. 计算机技术与发展， 2010，20（2）：114-116.

[11]随机森林算法优化研究[D]. 北京：首都经济贸易大学， 2014.

[12]丁世飞，齐丙娟，谭红艳. 支持向量机理论与算法研究综述[J].  电子科技大学学报， 2011， 40（1）：2-10.

[13]姚清耘. 基于向量空间模型的中文文本聚类方法的研究[D]. 上海：上海交通大学，2008.

[14]王之仓. 多层感知器学习算法研究[D]. 苏州：苏州大学，2006.

[15]朱大奇. 人工神经网络研究现状及其展望[J]. 江南大学学报， 2004，3（1）：103-110.

[16]卷积神经网络研究综述[J]. 计算机学报，2017，40（6）：1229-1251.

[17]朱小燕，王昱，徐伟. 基于循环神经网络的语音识别模型[J]. 计算机学报，2001，24（2）：213-218.

[18]丁建立，陈增强，袁著祉.  遗传算法与蚂蚁算法的融合[J]. 计算机研究与发展，2003，40（9）：1351-1356.

[19]段海滨，王道波，朱家强，等. 蚁群算法理论及应用研究的进展[J]. 控制与决策，2004，19（12）：1321-1326.

[20]模拟退火算法的研究及其应用[D]. 昆明：昆明理工大学，2005.

[21]高阳，陈世福，陆鑫. 强化学习研究综述[J]. 自动化学报，2004，30（1）：86-100.

[22]庄福振，罗平，何清，等. 迁移学习研究进展[J]. 软件学报，2015，26（1）：26-39.

（责任编辑：孙 娟）

收稿日期：2019-05-14

基金项目：国家自然科学基金项目（61650102）;广西自然科学基金项目（2018GXNSFBA281086）;广西高校中青年教师基础能力提升项目（KY2016YB278）;廣西高校科学计算与智能信息处理重点实验室开放项目（GXSCIIP201603）

作者简介：陶阳明（1987-），男，南宁师范大学计算机与信息工程学院硕士研究生，研究方向为人工智能自主学习算法设计。