基于时域卷积与双向GRU神经网络的时序预测模型
王振 张生


摘 要:随着物联网技术和5G技术的发展,各类智能设备收集的时序数据规模急剧增长,为了利用深度学习技术对大规模时序数据进行预测,提出一种基于深度神经网络的时序预测模型。该模型首先利用时域卷积神经网络层对时序数据进行预处理,然后利用双向GRU神经网络层提取时序数据的前向特征和后向特征,最后对时序数据进行预测。在真实数据集上的实验结果表明,该模型相比传统长短期记忆网络模型,预测准确度提高了近70%,预测速度提高了近10%,可更好地满足对大规模时序数据的预测需求。
关键词:深度学习;时序预测;双向GRU神经网络;卷积神经网络;循环神经网络
DOI:10. 11907/rjdk. 192539
中图分类号:TP306 文献标识码:A 文章编号:1672-7800(2020)003-0048-05
Time Series Prediction Model Based on Time Domain Convolution and
Bidirectional GRU Neural Network
WANG Zhen, ZHANG Sheng
(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
Abstract: With the development of Internet of Things and 5G technology, the scale of time series data collected by various kinds of intelligent devices has increased dramatically. In order to use deep learning technology to predict large-scale time series data, this paper proposes a time series prediction model based on deep neural network. This model firstly preprocesses the time series data with the time-domain convolutional neural network layer, then extracts the forward and backward characteristics of the time series data with the bidirectional gated recurrent unit (GRU) neural network layer, and finally predicts the time series data. The experimental results on real data sets show that the model proposed in this paper can better meet the prediction requirements of large-scale time series data by improving the prediction accuracy nearly 70% and the prediction speed nearly 10% compared with the traditional LSTM network model.
Key Words: deep learning; time series prediction; bidirectional GRU neural network; CNN; RNN
0 引言
序列數据通常包括文本数据和时序数据,其中时序数据反映数据在时间维度上的变化规律,其是按时间顺序存储的一连串随时间推移测量相同事物的数据点[1-2]。时序数据在现实生活中分布广泛,如智能家居系统在持续监控房屋内变化时收集的温度和湿度数据、自动驾驶汽车持续收集的环境变化数据等。时序预测即使用特定的时序预测模型对历史数据进行拟合,分析时序数据发展规律,最终对未知数据作出预测[2]。现有时序预测方法主要分为统计学习方法和深度学习方法,其中统计学习方法适用于线性时序数据预测,深度学习方法适用于复杂非线性的大规模时序数据预测[3]。
目前时序预测领域常见的深度学习模型为门控循环单元网络模型(Gated Recurrent Unit,GRU)[9],该模型通过隐层状态机制实现对时序数据历史信息的利用,通过门控机制实现对隐层状态的更新,该模型可较好地实现对中等规模时序数据的预测分析。但由于模型结构较为复杂,对大规模数据进行预测时运算速度较慢,且在数据规模较大时,隐层状态机制对较早的信息无法进行有效利用,导致准确度下降[2-3]。
为了更好地对大规模时序数据进行预测,本文提出一种基于时域卷积与双向GRU神经网络的时序预测模型。该模型首先构建包含时域卷积层和最大池化层的时域卷积神经网络,通过引入滑动窗口机制及最大池化结构,对大规模时序数据进行有效信息提取并缩减数据规模,然后利用双向GRU神经网络进行时序预测,有效避免了传统模型中无法有效利用隐层信息的问题,以提高对大规模时序数据的预测准确度与速度。
1 相关理论
1.1 卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN)是由LeCun[4]于1998 年提出的一种神经网络模型。卷积神经网络是一种前馈神经网络,是一种主要应用于计算机视觉领域的经典深度学习模型,相较于传统神经网络,其引入了卷积层和池化层。
卷积层(Convolutional Layer)用于将输入图像特征图与卷积核进行卷积运算,其通过滑动一个比原有输入尺寸更小的窗口提取输入的局部特征,然后在更高层进行合并,以得到输入图像全局特征。卷积层内部采用稀疏连接和权值共享机制,可以降低参数数量。
池化层(Pooling Layer)主要用于对数据进行池化处理,通常在卷积操作之后进行。池化处理的目的是为了计算特征在局部的充分统计量,从而降低总体特征数量,防止过拟合且减少计算量,同时通过增大卷积层的观察窗口,引入空间过滤器的层级结构。
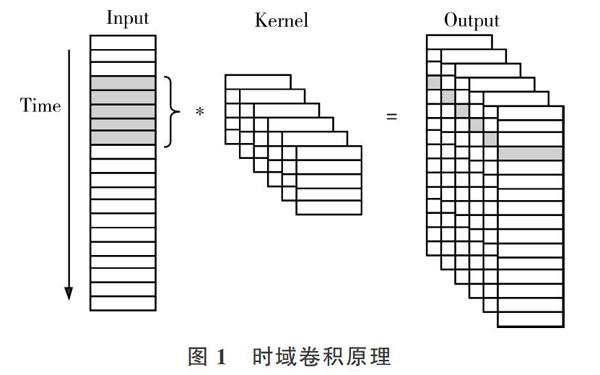
时域卷积神经网络是一种使用一维卷积核(One Dimensional Convolution Kernel)[5]在时域上对时序数据进行卷积计算的卷积神经网络,其工作原理如图1所示。它将时序数据中的时间维度看作一个空间维度,通过时序分割从序列中提取出局部序列段,然后使用一维卷积核对局部序列段的邻近信号进行卷积计算,生成一个输出张量。
时域卷积计算如式(1)所示。
式中[yt]表示[t]时刻的时域卷积值,[xt-k+1]表示输入序列[x={x1,x2,?,xn}]中的第[t-k+1]个值,[wk]表示一维卷积核中的权值参数,卷积核长度为[N]。
由于时域卷积神经网络的每个输出张量都是通过对不同位置上的局部序列段使用同一离散卷积核进行卷积计算得出的,即卷积核参数是固定的,因此时序特征在时间维度上的平移不会对时域卷积神经网络产生影响。所以与传统卷积神经网络类似,时域卷积神经网络在时间维度上具有平移不变性,可以识别出隐含在局部序列段中的局部特征模式。
由于时域卷积神经网络在对输入序列进行处理时没有保留输入时间步的顺序信息,因此为了加入时序敏感性,本文引入双向GRU网络对时域卷积神经网络的输出作进一步处理。
1.2 循环神经网络
循环神经网络(Recurrent Neural Networks,RNN)是一类具有内部环的神经网络[6]。其序列处理方式是:遍历序列元素,并生成一个隐层状态,其中包含与历史数据相关的模式信息。其能够保留序列前后关系,通常被用于处理序列数据。
对于传统循环神经网络,当输入序列长度较大时,会产生梯度消失问题,导致RNN实际上只能学习到短期依赖关系,而无法很好地处理远距离依赖,也称为长期依赖问题(Long-Term Dependencies Problem)[7]。
为了解决这一问题,一种比较好的解决方案是通过引入门控机制以控制信息累积速度,包括选择性地加入新信息,并选择性地遗忘之前累积的信息,通常称这类网络为基于门控的循环神经网络(Gated RNN)。两种常见的基于门控机制的循环神经网络为:长短期记忆网络(Long Short-Term Memory,LSTM)[8]和門控循环单元网络(Gated Recurrent Unit,GRU)[9]。
LSTM神经网络由Hochreiter&Schmidhuber于1997年提出,其是循环神经网络的一种变体。GRU神经网络由Chung等提出,其在LSTM基础上作进一步优化,使得运行计算代价更低。GRU与LSTM可得到同样准确的预测结果,而且GRU模型中包含网络参数更少,因此其运算性能较好,且降低了出现过拟合的风险。LSTM与GRU网络均使用被称为“门”(gate)的记忆模块或结构控制对历史序列特征的记忆。
在数字电路中存在着类似的“门”机制,其中 “门”为一个二值变量:{0, 1},0代表关闭状态,不允许任何信息通过;1代表开放状态,允许所有信息通过。GRU网络中的“门”是一种非离散数值,取值在(0, 1)之间,表示允许一定比例的信息流通过“门”。趋近于0时,表示信息流不能通过“门”;趋近于1时,表示信息流可以通过“门”。
门控循环单元模型内部结构如图2所示,设输入时序数据为[x={x1,x2,?,xt}],其中[xt]表示输入序列中第t个元素值;[ht-1]表示在t-1时刻的隐层状态;[rt]表示重置门,用于控制前一时刻隐层单元[ht-1]对当前输入[xt]的影响,若其值为0,则开关[rt]为打开状态,使[ht-1]对[xt]不产生影响;[zt]表示更新门,用于决定是否忽略当前输入[xt],当[zt]开关接通下方支路时,将忽略当前输入,同时在[ht-1]与[ht]之间形成短路,使得梯度得以有效地进行反向传播。这种构成短路的机制能够有效避免出现梯度消失现象。
在[t]时刻,门控循环单元模型在数学上的形式化表示如下:
其中,公式(2)和公式(3)中的[σ]表示Sigmoid激活函数,公式(4)和公式(5)中的[⊙]表示逐元素相乘,公式(6)为Sigmoid激活函数的数学定义。
2 模型
2.1 模型结构
本时序预测模型基本结构如图3所示。通过卷积计算与最大池化处理过程,将较长的原始时序数据转换为由抽象特征组成的更短序列,然后将其作为双向GRU网络层的输入进行分析处理。本时序数据预测模型充分结合了时域卷积神经网络在处理时序数据时的速度优势与门控循环单元的时序敏感性。
本模型通过引入时域卷积神经网络,一方面缩小了输入数据的数量级规模,提高了模型运算速度,另一方面时域卷积神经网络输出中隐含了较大时间跨度下的时序特征,使双向GRU网络进行后续计算时可以观察到更早的时序数据,以及分辨率更高的时序数据,从而提高了时序预测的准确性。
2.2 时域卷积神经网络处理层
在时域卷积神经网络处理层的卷积计算过程中使用128个时域卷积核,大小为24,最大池化层的最大池化算子大小为3。
时域卷积神经网络处理层激活函数为线性整流函数(Rectified Linear Unit,ReLU),又称为修正线性单元。ReLU函数可以使一部分神经元输出为0,以提高网络稀疏性,并且减少了参数的相互依存关系,以避免发生过拟合现象[11]。另外ReLU函数的导数为1,可减轻梯度消失问题,其数学定义如式(7)所示。
式中[x]为神经元输入量,[w]为神经元权重参数,[b]为神经元偏移量(bias)。
通过池化处理可以对输入数据进行缩放映射,在本模型中采用最大池化(Max Pooling)方法进行池化处理。通过最大池化处理可以在输入特征中提取局部最大值,以降低可训练参数数目,提高模型的鲁棒性[12]。
最大池化处理在减小输出数据维度的同时,保留了输入数据最显著的特征信息[13]。最大池化的意义主要为两点:一是通过对特征图(Feature Map)降维,有效减少后续层需要的参数;二是保持平移不变性(Translation Invariance) [14],即当输入数据在邻域发生微小位移时,最大池化层的输出是不变的,从而增强神经网络的鲁棒性,有一定的抗扰动作用。
最大池化变换函数如式(8)所示。
式中,[qli(t)]表示第[l]层第[i]个特征矢量中第[t]个神经元的值,[t∈[(j-1)W+1,jW]],[W]为池化区域宽度,[pl+1i(j)]表示第[l+1]层中第[j]次池化计算对应的值。
2.3 双向GRU神经网络处理层
由于时序信息在GRU网络中向前传递时会不断衰减,越靠前的序列信息衰减越严重。为了克服信息衰减问题,本文对GRU网络加以改进,同时训练两个方向相反的GRU以构成双向GRU模型[10]。双向GRU模型由两个单向GRU叠加在一起组成,每个时刻t的输入都会同时提供给两个方向相反的GRU网络层进行学習,模型最终输出由这两个单向GRU网络层输出共同决定。
本文使用的双向GRU神经网络模型如图4所示。
在双向GRU模型中,对前向传递和后向传递两个子GRU网络的输出进行叠加,可得到双向GRU模型输出,其输出公式如式(9)所示。
在双向GRU神经网络处理层中,前向传递子层与后向传递子层的神经单元个数均为32个。
为了避免模型在训练过程中出现过拟合,在门控循环单元处理层引入Dropout机制[15]。Dropout是指在深度学习网络训练过程中,对于神经网络单元,按照一定概率将其暂时从网络中丢弃,该机制可以增强模型的泛化性,因为其不会太依赖于某些局部特征。经过实验测试,当设置门控循环单元的Dropout为0.5时,模型性能达到最优。
3 实验
3.1 数据集与测试环境
本实验采用两个数据集,分别是美国PJM公司的电力负荷数据集(包含2002-2018年间收集的145 366条电力能源消耗数据,其时间粒度为每小时,单位为兆瓦(MW)),以及德国马克思·普朗克生物地球化学研究所的气象站数据集(包含2009-2018年间收集的420 551条气象观测数据,时间粒度为每10分钟),分别记为数据集1和数据集2。本实验在这两个数据集上将本模型与现有时间序列分析预测模型进行比较,最终证明本模型在解决实际问题时有较好表现。
在本实验输入数据中以每10分钟为一个时间步,每6个时间步(即每小时)采集一次数据,给定过去2 880个时间步(20天)之内的数据,以预测144个时间步(24小时)之后的时间序列数据。
实验在配置为Intel Core i5-4560 2.80GHz CPU、16GB内存、1TB硬盘,操作系统为Windows 10 64位的机器上进行,模型测试代码使用Python语言实现。在实验中,通过将本模型与常见的BP神经网络模型、RNN神经网络模型、LSTM神经网络模型及GRU神经网络模型进行对比,以证明本模型的高效性与准确性。
3.2 数据预处理
在将实验数据输入神经网络之前,需要对其进行预处理。由于各个时序数据集中数据的数值变化范围不同,为便于比较,需要对每个时间序列进行标准化(Standardization)处理。处理方法采用z-score标准化方法,具体是将原始时序数据的均值与标准差进行标准化,经过标准化处理后的时序数据符合标准正态分布,即均值为0,标准差为1,其转化函数如式(10)所示。
式中[xi]表示原始数据中的第[i]个值,[μi]表示原始数据均值,[σi]表示原始数据标准差,[xi]表示标准化后的数据。
3.3 评价指标
为了验证本模型相对其它时序预测模型的优势,本实验引入平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)、均方误差(Mean Squared Error,MSE) [16]与算法运行时间4项评估指标。通过该评价指标,可以充分评估各个时序预测模型在测试集上的预测误差和预测速度。
其中MAE是指模型预测值[yi]与样本真实值[yi]之间距离的平均值,MAE能够较准确地反映预测值误差的真实情况。MAE值越小,预测精度越大。MAE计算公式如公式(11)所示。
上式中[m]为测试集中的样本个数,[yi]、[yi]分别表示第[i]个样本的真实值和预测值。
RMSE表示模型预测值[yi]与样本真实值[yi]之间差异的样本标准偏差,RMSE对于测试集中的异常数据点更加敏感,即若有一个预测值与真实值相差很大,RMSE则会很大。RMSE值越小,预测精度越大。RMSE计算如式(12)所示。
MSE是指参数估计值与参数真实值之差平方的期望值,可用于评价数据变化程度,MSE值越小,说明预测模型具有更好的精度。MSE计算如式(13)所示。
3.4 实验结果分析
表1、表2列出了使用MSE、MAE、RMSE与算法运行时间4种评价指标对BP神经网络模型、RNN神经网络模型、LSTM神经网络模型、GRU神经网络模型及本文模型在不同数据集上进行评估的结果。
对比实验结果显示,本模型在数据集1与数据集2上的MSE评估指标相比LSTM神经网络模型分别提升了30.12%、70.31%,运行时间指标分别提升了12.81%、10.5%。相比单层GRU神经网络模型,加入时域卷积网络后的模型在数据集1与数据集2上的MSE评估指标分别提升了45.41%、69.14%,运行时间指标分别提升了8.5%、5.7%。说明通过结合时域卷积与双向GRU神经网络,本模型减小了运算负荷,且能够捕获更长时间维度中的时序信息,进而提高了本模型的预测准确性与速度。
为了验证模型实际性能,图5中给出了本模型时序预测结果与真实值的对比。结果显示,本模型对时序数据的趋势预测基本正确,说明从时域卷积神经网络提取的显著性特征中,双向GRU网络可以获得更准确的时序规律,有效提高了时序预测精度,可满足实际应用需要。
4 结语
在未来的高速、低延时5G网络中,种类多样的物联网传感器将产生大量时序数据。针对当前时间序列预测中存在的准确性与计算效率较低的问题,本文提出一种基于时域卷积与门控神经单元的网络模型对时序数据进行预测。相比浅层的传统模式识别方法,本模型可避免人工特征提取,并增强了模型泛化能力。最终实验结果表明,相较于BP神经网络模型、RNN神经网络模型、LSTM神经网络模型与GRU神经网络模型,利用本模型进行时序预测有着更高的准确度与速度。在未来研究中,还会对本模型的神经网络结构进行优化,以进一步提高模型预测精度和速度。
参考文献:
[1]WEIGEND A S. Time series prediction: forecasting the future and understanding the past[M]. Routledge, 2018.
[2]潘丽娜. 神经网络及其组合模型在时间序列预测中的研究与应用[D].兰州:兰州大学,2018.
[3]汤铃. 复杂时间序列预测技术研究[M]. 北京:科学出版社,2016.
[4]LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J].Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[5]HAIDAR A,VERMA B. Monthly rainfall forecasting using one-dimensional deep convolutional neural network[J]. IEEE Access, 2018, 6: 69053-69063.
[6]LIPTON Z C, BERKOWITZ J, ELKAN C. A critical review of recurrent neural networks for sequence learning[J]. arXiv preprint arXiv:1506.00019, 2015.
[7]BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE transactions on neural networks, 1994, 5(2): 157-166.
[8]HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.
[9]CHUNG J, GULCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[DB/OL].https://arxiv.org/pdf/1412.3555.pdf.
[10]LU R,DUAN Z. Bidirectional GRU for sound event detection[J]. Detection and Classification of Acoustic Scenes and Events, 2017.
[11]LI Y, YUAN Y. Convergence analysis of two-layer neural networks with relu activation[C]. Advances in Neural Information Processing Systems,2017:597-607.
[12]SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural networks,2015,61: 85-117.
[13]TOLIAS G, SICRE R, JéGOU H. Particular object retrieval with integral max-pooling of CNN activations[DB/OL]. https://arxiv.org/pdf/1511.05879.pdf.
[14]BOROVYKH A, BOHTE S, OOSTERLEE C W. Conditional time series forecasting with convolutional neural networks[EB/OL]. https://www.doc88.com/p-4935081904951.html.
[15]SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting [J]. The Journal of Machine Learning Research, 2014, 15(1):1929-1958.
[16]MORIASI D N,ARNOLD J G,VAN LIEW M W,et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE,2007,50(3):885-900.
(责任编辑:黄 健)
收稿日期:2019-11-02
基金项目:上海市科学技术委员会科研计划项目(17511109102)
作者简介:王振(1993-),男,上海理工大学光电信息与计算机工程学院硕士研究生,研究方向为深度学习、时序预测;张生(1968-),男,上海理工大学光电信息与计算机工程学院高级工程师,研究方向为工业自动化、深度學习。

