上游泵送机械密封润滑膜固体颗粒沉积特性研究

陈汇龙，桂铠，韩婷，谢晓凤，陆俊成，赵斌娟

（江苏大学能源与动力工程学院，江苏镇江212013）

引 言

上游泵送机械密封主要是利用密封端面泵送槽的泵送效应和流体动压效应，实现密封动静环之间的非接触，理论上可实现被密封介质的零泄漏甚至零逸出[1-3]。同时，由于上游泵送机械密封端面间形成的微米级润滑膜能有效改善端面润滑条件，达到了降低摩擦和减少磨损的目的，因此已被广泛应用于石油化工等相关领域[4-5]。

在上游泵送机械密封实际运行过程中，除了密封介质会将微小固体颗粒带入密封间隙外，端面泵送槽的泵吸作用也极易将下游空气或冲洗冷却液夹杂的微小固体颗粒吸入到密封端面润滑膜中。这些固体颗粒的进入，一方面使润滑膜流场特性发生变化，另一方面会出现沉积现象，严重时将会导致泵送槽的堵塞甚至丧失泵送能力，造成机械密封端面摩擦功耗的增加和密封端面的加剧磨损[6-7]。据统计，发生故障的机械密封中近一半是由于颗粒磨损造成的[8]。固体颗粒在间隙润滑膜中的运动、沉积规律与润滑膜多相流动特性密切相关，此外由于密封端面微造型或带有波纹等，当润滑膜局部压力低于饱和蒸气压时将出现空化现象，进一步增加了润滑膜中固体颗粒运动沉积的复杂性[9-10]。因此，深入研究掌握润滑膜中固体颗粒沉积特性是设计性能优秀、运行稳定的上游泵送机械密封必须面对的重要问题之一。

对于密封腔含固体颗粒流场的研究，Merati等[11]在考虑叶片上平衡孔的影响下，针对锥形密封腔内固体颗粒的运动进行了试验研究，得到了不同条件下的颗粒轨迹及分布情况，发现粒径大约为40 μm 的固体颗粒会随流做螺旋运动，而大直径颗粒则聚集于底面并沿螺旋轨迹移动，造成了密封腔表面的磨损。Azibert 等[12-13]采用离散相模型对不同工况下的离心泵机械密封密封腔流场进行了数值模拟，并针对固体颗粒聚集于密封端面附近这一现象设计了一种带有固体分离装置的离心泵机械密封，计算得到了不同流体黏性、不同冲洗条件下的固体颗粒分布情况。赵龙[14]针对带有固体颗粒的不同尺寸机械密封密封腔进行了固液两相流数值模拟，发现在锥形密封腔以及带冲洗液情况下排出固体颗粒效果更好。对于密封间隙含固体颗粒流场的情况，严彦等[15]对一种动环开设引流孔的双向自泵送流体动静压型机械密封泵入和泵出时的工作性能进行了研究，发现这种自泵送流体动静压型机械密封在两种工作方式下都具有良好的抗颗粒干扰性。Chen 等[16]在此基础之上，基于Fluent 软件计算分析，得到了其在不同颗粒直径、转速、压差、液膜厚度和颗粒体积浓度下的自清洁特性。彭旭东等[17]以核主泵所用U 型槽动压密封环为对象，对介质中的杂质颗粒对密封端面的磨损问题展开了研究，结果表明端面动压槽根部产生的初期磨损会导致润滑膜刚度和泄漏率增大。陈汇龙等[18]采用Mixture 模型对上游泵送机械密封润滑膜固液两相流动特性进行了研究，得到了密封端面润滑膜内部微小固体颗粒的分布规律及其对密封性能的影响。Chen 等[19-20]基于欧拉多相流模型建立了密封微间隙气液固多相流动计算模型，得到了间隙密封气液固多相润滑膜的内流场特性并研究了固体颗粒的直径、颗粒进口体积分数、气核含量等气-固相物理参数对润滑膜空化及润滑性能的影响关系。从现有国内外研究来看，关于机械密封端面微间隙润滑膜中固体颗粒的运动特性及分布规律的研究已取得一定的进展，但仍不够系统深入，尤其是对固体颗粒沉积特性的研究还很缺乏，加强这方面的研究具有重要的理论和现实意义。

本文利用Fluent 中的DPM 模型，考虑双向耦合作用，结合空化模型进行数值模拟，以清水为密封介质，研究固体颗粒直径、颗粒进口体积分数、转速、介质压力、润滑膜厚度等对上游泵送机械密封端面润滑膜固体颗粒沉积特性的影响规律，为提高上游泵送机械密封性能及适应能力提供参考依据。

1 物理模型

1.1 几何模型

图1 为典型的上游泵送机械密封端面造型[21]。螺旋槽开在动环端面，型线为对数螺旋线，在极坐标下描述为

式中，ri为螺旋槽内半径，mm；φ 为螺旋线展开角，(°)；α为螺旋角，(°)。

图1 机械密封端面螺旋槽造型Fig.1 Face structure of spiral groove mechanical seal

利用三维造型软件建立参数化螺旋槽上游泵送机械密封微间隙润滑膜几何模型，其参数为: 螺旋槽内半径ri= 26 mm；密封面外半径ro=31 mm；槽根圆半径rg=28.5 mm；螺旋角α=21°；槽宽比γ=0.5；槽径比β=0.5；槽深hc=8 μm；密封间隙润滑膜厚度h=3 μm；槽数Ng=12。密封间隙润滑膜三维模型如图2 所示，为便于观察，在膜厚方向放大1000 倍表示。

1.2 网格划分及边界条件

图2 端面润滑膜三维模型Fig.2 Three-dimensional model of lubricating film

由于螺旋槽呈周期性排列，故只选取润滑膜的1/Ng作为计算域，在前处理软件Gambit 中采用非结构网格进行网格划分。为了提高计算效率和准确性，网格划分过程中进行了网格无关性检验，针对33万～172万不同网格数的网格进行模拟计算，衡量参数为开启力与固体颗粒沉积率，运行转速为3000 r/min，介质压力为0.2 MPa。不同网格方案的润滑膜固体颗粒沉积率、开启力计算结果如图3 所示。由图3 可知，随着网格数增大，计算偏差逐渐减小，网格数量超过59万以后计算结果基本不变，此时认为网格数对计算结果的影响很小，综合考虑收敛速度与精确度，采用59 万网格方案，最终网格划分结果如图4所示。

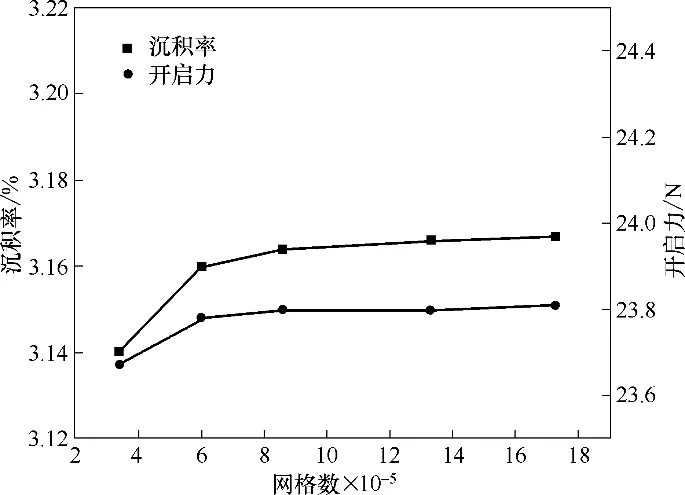
图3 网格无关性检验Fig.3 Grid independence verification

图4 1/Ng润滑膜网格及边界条件Fig.4 1/Ng lubrication film mesh and boundary conditions

在Gambit 中设置如图4 所示的边界条件，螺旋槽内润滑膜设置为旋转水体；微间隙内润滑膜设置为静止水体；动环表面、螺旋槽的轴向三个侧面及槽底面均设置为旋转运动壁面，静环表面设置为静止壁面。进口压力为密封介质压力，取值范围为0.2～1.6 MPa，出口压力为大气压力0.101325 MPa，转速取值范围为1000～6000 r/min。

2 数学模型

2.1 基本假设

本文以清水为密封介质，即间隙内流场连续相为清水，离散相固体颗粒的密度为3450 kg/m3，黏度折合连续介质的黏度为0.04 Pa·s[22]，颗粒直径范围为0.25～3.0 μm，颗粒体积分数在10%以下。为了降低上游泵送机械密封润滑膜流场计算的复杂性，忽略对计算结果影响较小的因素，本文根据研究对象的特点作如下假设[23-25]：

（1）间隙液体流动为层流且为不可压缩流体；

（2）忽略润滑膜受温度的影响，且介质温度、黏度保持不变；

（3）润滑膜与密封端面无相对滑移；

（4）忽略密封环粗糙度的影响；

（5）固体颗粒均为球形且大小均匀，不考虑相变；

（6）润滑膜与固体颗粒保持恒温25℃，即不考虑颗粒的热泳力、布朗力及热辐射；

（7）忽略Magnus 升力、Saffman 力、Basset 力、附加质量力与科氏力。

2.2 连续相基本方程

混合物模型的连续性方程为[26-28]

混合物的动量方程可以通过对所有相各自的动量方程来获得，可表示为

由第二相( p) 的连续性方程，可得第二相的体积分数方程为

式中，ρm为混合密度，kg/m3；vm为质量平均速度，m/s；μm为混合黏性系数，Pa·s；F为体积力，N；n为相数；αk为第k 相的体积分数；ρk为第k 相的密度，kg/m3；vdr,k为第k相的漂移速度，m/s。

2.3 离散相基本方程

根据上述基本假设，固体颗粒在密封润滑膜气液固流场中主要受到压强梯度力FP、绕流阻力FD、重力Fg及由于旋转施加在颗粒上的离心力F离等作用力，因此离散相固体颗粒在Lagrangian 坐标系下的受力平衡方程为[29]

其中，

式中，Cd为曳力系数；mp为颗粒质量，kg；up为颗粒速度，m/s；ρ 为流体密度，kg/m3；u 为流体速度，m/s；ρp为颗粒密度，kg/m3；dp为颗粒直径，m；∇p 为压力梯度，Pa/m；ωp为旋转轴角速度，rad/s。

2.4 DPM模型选择与计算流程

密封间隙固体颗粒来源通常有三个方面，即密封介质含有固体颗粒、密封端面磨损产生固体颗粒、螺旋槽内径负压吸入环境固体颗粒等，考虑到问题的复杂性，本文暂选择固体颗粒从螺旋槽内径侧吸入的问题进行模拟研究。由于本文研究的上游泵送机械密封润滑膜中离散相的体积比很小且颗粒群的控制体积大小并非远小于流场尺寸，因此本文选取DPM模型进行模拟计算[30]。

本文先计算连续相稳态流场直至收敛，再加入离散相颗粒计算求解，连续相每计算10步后进行颗粒轨迹追踪直至收敛，同时考虑离散相与连续相的双向耦合作用。模拟过程中假设颗粒直接在入口存在且均匀分布，即颗粒入射初速度为0。将螺旋槽内径侧与外径侧定义为Escape 边界，其他所有面定义为Reflect 边界且均为完全弹性碰撞，反弹系数为1，计算流程如图5所示。

2.5 空化模型选择

目前Fluent 中有两种空化模型,即Zwart-Gerber-Belamri 空 化 模 型[31]和Singhal 等[32]的 空 化 模型。Singhal 等的空化模型主要考虑了不可冷凝气体对空化的影响，适合应用于存在液相相变、湍流压力脉动等场合。而Zwart-Gerber-Belamri 空化模型假设空化产生的气泡尺寸相同，局部均衡性更好，同时也相对比较成熟。因为本文的密封介质为清水，密封端面微间隙流动为层流，也并未考虑液相相变的情形，同时从文献[33-35]可知，采用Zwart-Gerber-Belamri 空化模型的计算模拟结果比Singhal 等的空化模型更接近试验值，稳定性也较好，因此本文选用Zwart-Gerber-Belamri 空化模型。空化边界条件为：当润滑膜内局部压力小于饱和蒸汽压力时，空化发生，空泡内压力为饱和蒸汽压力且泡壁压力梯度为0，饱和蒸汽压力为3540 Pa。

图5 计算流程图Fig.5 Flow chart of calculation

2.6 求解设置

采用三维双精度求解器，求解器基于压力速度耦合SIMPLEC 算法求解，扩散相梯度差值采用Least Squares Cell Based 格式，动量采用一阶迎风差分格式，体积分数采用一阶迎风差分格式，收敛精度为10-5。

3 计算结果及分析

一定量的颗粒由润滑膜内径侧进入后，一部分将在运动中通过润滑膜内径侧或外径侧离开润滑膜分别返回下游或进入密封腔，剩余的部分则沉积在密封润滑膜中，为此，将残留在润滑膜中的颗粒数与从润滑膜内径侧进入的总颗粒数之比定义为固体颗粒在机械密封润滑膜中的沉积率。

3.1 模型有效性验证

为了检验本文模型设置的正确性，采用本文模拟方法计算文献[36]中螺旋槽气体动压轴承槽数为12 时亚微米级颗粒物沉积数量随颗粒直径的变化规律，计算结果如图6 所示。由图6 可知，本文模拟方法得到的结果与文献吻合较好。

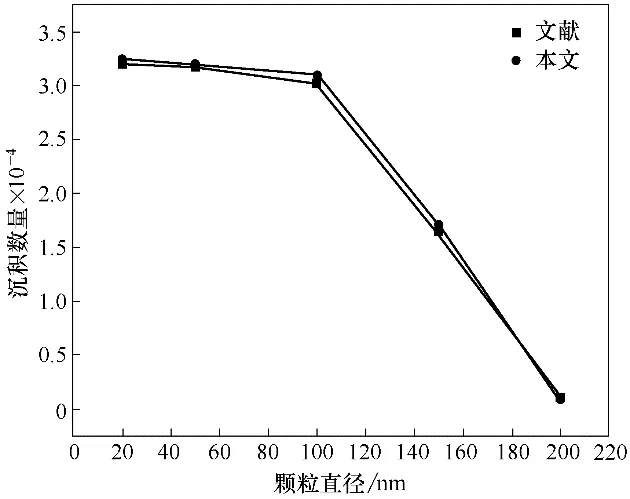
图6 固体颗粒沉积数量模拟结果对比Fig.6 Comparison of simulation results of solid particle deposition

3.2 连续相流场

图7 为转速3000 r/min、介质压力0.2 MPa、颗粒直径3 μm、颗粒进口体积分数10%、润滑膜厚度3 μm 时，连续相流场稳定后的润滑膜压力分布以及气泡相体积分数分布情况。由图7（a）可见，在螺旋槽外槽根处存在高于介质压力的最大静压，并以此为中心形成压力梯度，在坝区起到局部阻止高压侧液体向低压侧流动的作用，而在螺旋槽迎风侧堰区存在局部可能促进泄漏的作用；同时在螺旋槽内槽根至背风侧堰区存在低压区，能够将高压侧流向低压侧的泄漏液体吸收并向高压侧泵送，起到减少或杜绝泄漏的作用。局部空化出现在螺旋槽背风侧中部堰区，如图7（b）所示。

3.3 颗粒直径对沉积分布及沉积率的影响

图8 为不同颗粒直径下固体颗粒沉积分布云图。由图8 可知，沉积颗粒主要位于槽内低压区上游，空化区上游边界圆周和外槽根及其圆周上也出现沉积。说明固体颗粒进入槽区后，位于低压区且速度较低的颗粒，没能到达螺旋槽迎风侧获得剪切能量而导致沉积，进入空化区上游边界的颗粒受润滑膜周向流动的带动而沿周向分布，而进入剪切区的颗粒获得能量后一部分被外槽根拦截沉积并受外槽根周向压力梯度及连续相周向流动的带动而沿周向分布，另一部分到达坝区在离心力和压力梯度力作用下从外径侧逃逸。粒径较小时，较多沉积于低压区，粒径较大时空化外边界和外槽根圆沉积数量增大。

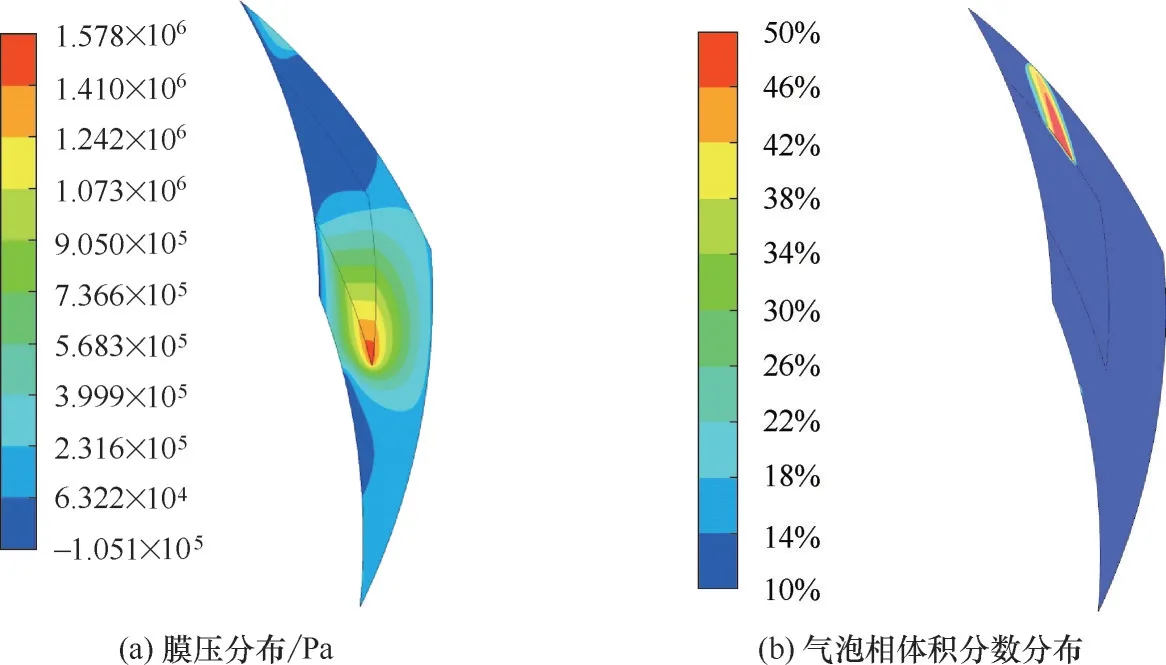
图7 连续相流场计算结果Fig.7 Calculation results of continuous phase flow field

图8 不同颗粒直径下固体颗粒沉积分布Fig.8 Deposition distribution of solid particles under different particle diameters

图9 为颗粒进口体积分数10%、介质压力0.2 MPa、转速3000 r/min、润滑膜厚度3 μm 时沉积率随颗粒直径的变化规律。

由图7、图9 可以看出，当颗粒直径为1～1.5 μm时，沉积率随颗粒直径的增大而较快增大，说明颗粒直径增大受到的离心力也增大，跟随性减弱，随密封泄漏液从内径侧逃逸的颗粒减少，同时，从螺旋槽剪切中获得能量而到达坝区的颗粒，虽然也因离心力增大而更易从外径侧逃逸，但其数量相对较小；当颗粒直径为1.5～2 μm 时，离心力仍增大，但指向内径的压强梯度力也增大，因此，从内径侧逃逸颗粒的减少趋缓，而外径侧逃逸颗粒因离心力和指向外径的压强梯度力的增大而增多，使沉积率略微下降；当颗粒直径继续增大至3 μm 时，内径侧逃逸继续减少，但因颗粒直径已逼近密封间隙尺寸，加上颗粒重力（指向动环面）增大，颗粒受外槽根拦截的概率增大，外径侧逃逸增多的速率下降，导致沉积率上升。绕流阻力因微颗粒总体跟随性较好，故影响相对较小。

图9 颗粒直径对沉积率的影响Fig.9 Influence of particle diameter on deposition rate

3.4 转速对沉积分布及沉积率的影响

图10 为固体颗粒直径为3 μm 时，不同转速下固体颗粒沉积分布云图。当转速为1000 r/min 时，颗粒主要聚集于槽区背风侧附近低压区，同时在密封外径侧出现沉积并沿周向分布，这是由于转速较低，最高膜压也较低，坝区径向压力梯度力较小，部分颗粒在内径侧随正泄漏（压力出口方向的泄漏）逃逸，而部分颗粒因未能从外径侧逃逸而沉积。当转速达到5000、6000 r/min 时，颗粒主要沉积于槽内低压区背风侧及外槽根内侧。说明较大的离心力和压力梯度力使到达坝区和堰区的颗粒基本随负泄漏从外径侧逃逸。

图10 不同转速下固体颗粒沉积分布Fig.10 Deposition distribution of solid particles under different speed

图11 为颗粒进口体积分数10%、进口压力0.2 MPa、润滑膜厚度3 μm 时颗粒不同直径下沉积率随转速的变化规律。图11 表明，随着转速的增大，沉积率虽有小波动但总体呈下降趋势。这说明转速较低时颗粒随正泄漏逃逸的数量低于高转速时随负泄漏逃逸的数量，转速增大导致颗粒受到的离心力和压力梯度力均增大，成为影响颗粒运动的主要因素，颗粒直径越大受影响越明显，转速越高从外径侧逃逸的颗粒越多。

图11 转速对沉积率的影响Fig.11 Influence of speed on deposition rate

3.5 介质压力对沉积分布及沉积率的影响

图12 为固体颗粒直径为3 μm 时，不同介质压力下固体颗粒沉积分布云图。由图12可见，介质压力的升高，总体上使外槽根处的固体颗粒向内径侧推移，特别是介质压力达到1.6 MPa 时，外槽根处及堰区空化部位基本没有沉积颗粒，说明介质压力升高阻碍了颗粒向外槽根运动，同时使堰区空化区域缩小甚至消失。

图12 不同介质压力下固体颗粒沉积分布Fig.12 Deposition distribution of solid particles under different medium pressure

图13 为颗粒进口体积分数10%、转速3000 r/min、润滑膜厚度3 μm 时不同颗粒直径下沉积率随介质压力的变化规律。由图13可知，在所研究的介质压力范围内不同直径颗粒的沉积率均随介质压力的增大而降低，且颗粒直径越大沉积率下降的幅度越大，说明介质压力的升高，增大了促使内径侧泄漏的润滑膜压强梯度力，导致从内径侧离开润滑膜的颗粒增多，沉积率下降，而颗粒直径越大所受的压强梯度力越明显，沉积率的下降也越明显。

图13 介质压力对沉积率的影响Fig.13 Influence of medium pressure on deposition rate

3.6 颗粒进口体积分数对沉积分布及沉积率的影响

图14 不同颗粒进口体积分数下固体颗粒沉积分布Fig.14 Deposition distribution of solid particles under different particle import volume fraction

图14 为固体颗粒直径为3 μm、转速为1000 r/min 时，不同颗粒进口体积分数下固体颗粒沉积分布云图。由图可知，固体颗粒主要聚集于螺旋槽低压区上游，但随着颗粒进口体积分数的提升，在螺旋槽低压区上游沉积量增大的同时，沉积部位向外槽根和坝区拓展，坝区的沉积颗粒沿周向分布。说明颗粒进口体积分数的提升，受到螺旋槽剪切而获得能量的颗粒明显增多，到达槽内高压区和坝区的颗粒增多，导致相应区域沉积量增加。

图15 为介质压力0.2 MPa、转速3000 r/min、润滑膜厚度3 μm 时不同转速下颗粒沉积率随颗粒进口体积分数的变化规律。由图15可知，随着颗粒进口体积分数的增大，沉积率总体呈现略微下降的趋势，在转速升高时出现微小波动但规律性不明显。这说明在相同的工况和颗粒直径下，由于研究中的颗粒进口体积分数较低，体积分数的变化对流场影响小，固体颗粒的受力及运动的变化也比较小，颗粒进口体积分数的改变主要是改变了沉积的绝对数量而已，对沉积率影响较小。至于随颗粒进口体积分数增大沉积率略有下降的现象，可能是由于颗粒进口体积分数的增大使多相流黏度和密度有所提升，动压效应有所增强，压强梯度力造成的从润滑膜内径侧逃离的颗粒增多的缘故。

3.7 润滑膜厚度对沉积分布及沉积率的影响

图16 为上述条件下转速1000 r/min 时，不同润滑膜厚度下固体颗粒沉积分布云图。可以看出，随着膜厚的增大，沉积区域明显由槽内低压区上游向背风侧下游和外槽根侧扩展，沉积量明显增加。这进一步说明压力梯度减弱的效应，此外，膜厚增大使进入润滑膜的颗粒绝对数增多和沉积量增大。

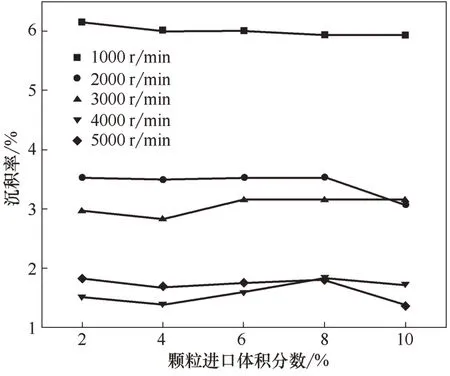
图15 颗粒进口体积分数对沉积率的影响Fig.15 Influence of particle import volume fraction on deposition rate

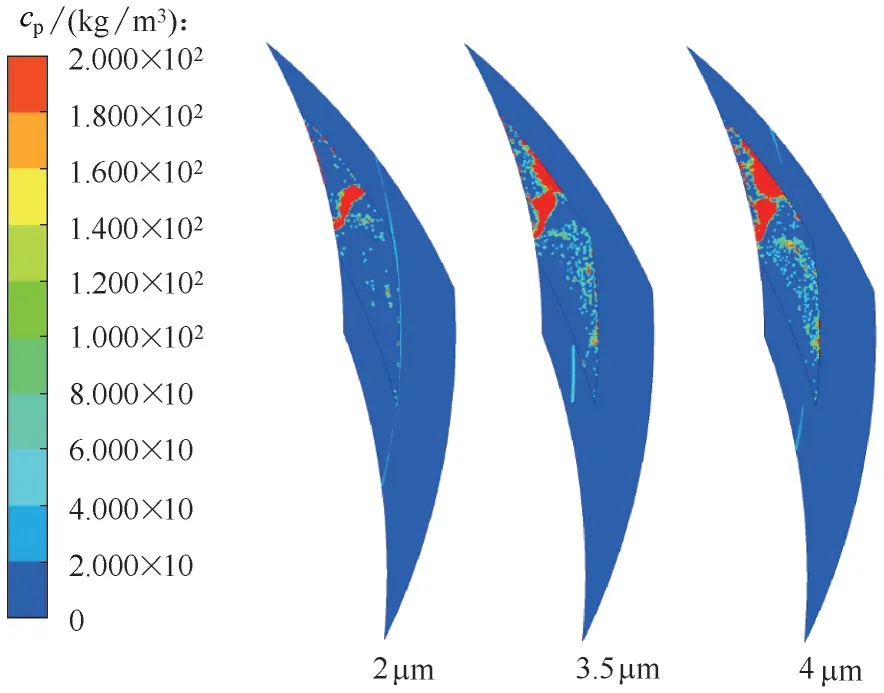
图16 不同润滑膜厚度下固体颗粒沉积分布Fig.16 Deposition distribution of solid particles under different thickness of lubricating film

图17 润滑膜厚度对沉积率的影响Fig.17 Influence of thickness of lubricating film on deposition rate

图17为介质压力0.2 MPa、颗粒直径2 μm、进口颗粒积分数10%时不同转速下颗粒沉积率随润滑膜厚度的变化规律。由图17可知，沉积率随着润滑膜厚度的增大呈波动上升趋势，转速越低波动越明显，沉积率上升也越明显。这是因为随着润滑膜厚度的增加，润滑膜压力下降，高压区与内外径侧的压力梯度减小，固体颗粒从内外径侧逃逸的数量减少，导致沉积率呈上升趋势，同时，由于膜厚增大，润滑膜刚度和稳定性减弱，可能是沉积率出现波动的原因。

4 结 论

在本文研究的参数范围内，经密封微间隙润滑膜气液固数值模拟分析得到如下结论。

（1）固体颗粒沉积率随颗粒直径的增大而明显增大，随转速的增大而降低且粒径越大下降越明显，随介质压力的增大而降低且粒径越大下降幅度越大，随颗粒进口体积分数的增大而呈略显下降趋势，随润滑膜厚度的增大而呈波动上升趋势且转速越低上升越明显。可见，粒径较小、转速增大、介质压力增大、膜厚减小有利于降低颗粒沉积率。

（2）螺旋槽低压区是固体颗粒沉积的主要部位，颗粒在螺旋槽内的沉积分布与粒径、转速、介质压力、颗粒进口体积分数和膜厚等参数的大小密切相关，粒径、颗粒进口体积分数、转速和膜厚增大，介质压力降低，会使沉积区域明显向外槽根拓展，这是螺旋槽易出现堵塞失效的原因。

（3）低转速时易在坝区出现颗粒沉积，且非槽区的沉积颗粒呈周向分布。

符 号 说 明

Cd——曳力系数

cp——固体颗粒质量体积浓度，kg/m3

dp——颗粒直径，m

F——体积力，N

FP,FD,Fg,F离——分别为固体颗粒受到的压强梯度力、绕流阻力、重力、离心力，N

h——密封间隙润滑膜厚度，μm

hc——槽深，μm

mp——颗粒质量，kg

Ng——槽数

n——相数

rg——槽根圆半径，mm

ri——螺旋槽内半径，mm

ro——密封面外半径，mm

u——流体速度，m/s

up——颗粒速度，m/s

vdr,k——第k相的漂移速度，m/s

vm——质量平均速度，m/s

α——螺旋角，(°)

αk——第k相的体积分数

β——槽径比

γ——槽宽比

μm——混合黏性系数，Pa·s

ρ——流体密度，kg/m3

ρk——第k相的密度，kg/m3

ρm——混合密度，kg/m3

ρp——颗粒密度，kg/m3

φ——螺旋线展开角，(°)

ωp——旋转轴角速度，rad/s