考虑需求响应及其不确定性的台区三相不平衡治理

刘国伟， 陈宏辉， 陈 童， 杨 永， 陈 阅， 马宇航

(1.广东电网有限责任公司 茂名供电局， 广东 茂名 525000； 2.四川大学 电气工程学院， 成都 610065)

我国低压配电台区数目众多、分布广泛，多为三相四线制供电模式，其中单相负荷占据绝对比重。由于各相负荷时空分布不均匀，台区存在着不同程度的三相不平衡现象。长期处于不平衡运行状态的台区主要面临以下4个问题：①变压器和线路损耗增加[1]；②重载相电压降低，轻载相电压升高，对用电设备造成不利影响；③降低变压器的运行效率与过载能力[2]；④变压器产生额外的涡流损耗，运行温度升高，使用寿命降低[3]。因此，亟需采取有效的治理措施应对台区三相不平衡，实现台区安全经济运行。

目前，台区三相不平衡治理方案主要有以下4种：①人工离线调整负荷相序[4]。该方案采用人工实地施工的方式调整电力用户的接入相别，能够在一定程度上缓解台区三相不平衡问题，但调整周期难以确定，可靠性低，施工时间长，调整期间用户供电中断，方案总体较为落后。②相间无功补偿[5]。该方案通过在变压器低压侧加装并联电容器等无功补偿装置实现三相不平衡治理，能够发挥一定的效用，但补偿方式不够灵活，无法适应实时变化的电力负荷，补偿效果有限。③三相负荷不对称调补[6-7]。该方案通过特定算法求取补偿导纳，利用并联补偿网络同时实现无功补偿与三相电流不平衡补偿，但存在控制策略复杂，治理成本高等问题。④采用低压负荷换相开关[8]。该方案通过安装在变压器低压侧的控制终端监测台区三相不平衡度，当三相不平衡度越限时，通过特定控制策略向安装在负荷侧的换相开关发出换相指令，实时调整负荷相位。该方案可靠性较高，但也需要额外的设备安装及运行维护费用，成本较高。

综上所述，目前的三相不平衡治理措施或是效率低下，可靠性差，或是需要安装额外的设备，治理成本较高，因此需要寻求一种面向未来台区智能化的低成本、高普适性的三相不平衡治理措施。随着我国电力体制改革的推进及电力市场的逐步开放，未来通过需求响应(demand response，DR)引导电力用户改变自身用电行为将成为电网公司实现与用户之间灵活交互的重要方式[9-10]。实现需求响应的措施有两种[11]：一是基于价格的需求响应(price-based demand response，PBDR)，利用用户负荷与电价之间的关联关系，通过改变电价影响用户的用电需求；二是基于激励的需求响应(incentive-based demand response，IBDR)，通过给予电力用户一定的补偿，使用户按照系统需求对自身负荷进行调整。需求响应已被应用在许多场景中，取得了丰富的研究成果，但尚未有文章在考虑需求响应的前提下对台区三相不平衡治理这一实际问题进行探索，因此如何有效利用需求响应对用户用电行为的影响，解决台区三相不平衡问题，是一项具有重要意义的研究。

本文以未来电力市场化环境下的智能台区为研究背景，考虑价格型需求响应，充分利用负荷的价格-需求响应特性，在给定日前台区负荷预测曲线的基础上，通过调整日前电价改变电力用户的用电曲线，达到降低三相不平衡度的目的。为了应对用户响应电价变化的不确定性，采用模糊变量与模糊机会约束规划对电力负荷进行处理，确保三相不平衡治理效果的客观有效性。

1 不确定性PBDR建模

在考虑价格型需求响应时，常采用需求弹性矩阵表征负荷变化量与电价变化量之间的关系[12]，则价格型需求响应模型如下：

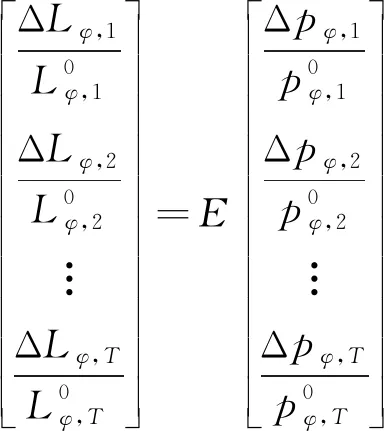
(1)

式中：T为总时段数，本文采用24 h作为三相不平衡优化时间尺度，各时段间隔为1 h；下标φ为电力用户的接入相别标识，φ∈{A, B, C}；L0φ,t为φ相用户t时段初始电力需求，本文采用该时段内总用电量表征用户电力需求；p0φ,t为φ相t时段初始电价；ΔLφ,t为φ相用户t时段实施需求响应后的电力需求变化量，Δpφ,t为φ相t时段实施需求响应后的电价变化量，分别由下式计算：

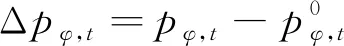
(2)

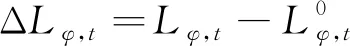
(3)

式中：Lφ,t为φ相用户t时段实施需求响应后的电力需求；pφ,t为φ相t时段实施需求响应后的电价。

式(1)中，E为价格型需求弹性矩阵，表征实施需求响应后的负荷变化率与电价变化率之间的关系，表达式如下：

(4)

式中：eii为用户需求的自弹性系数，eij为用户需求的互弹性系数，下标i和j为时段标识。eii一般为负值，表示某一时段电力需求变化与电价变化相反；eij一般为正值，表示某一时段电力需求变化与其他时段电价变化相同，需求弹性矩阵中的系数通过实地调查确定。上述模型所表示的电价—需求关系曲线如图1所示。

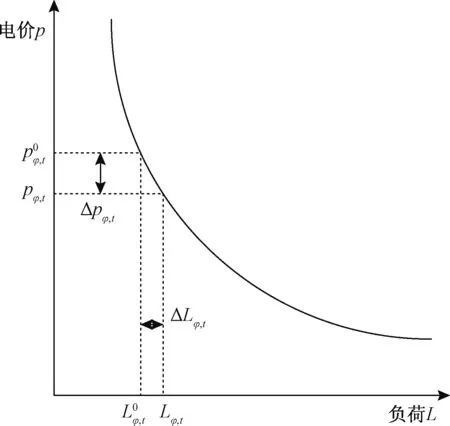
图1 电价型需求响应的电价—需求关系曲线

上述模型为确定性模型，然而实际价格型需求响应的实施效果会受到电力用户的主观意愿影响，因此具有一定的不确定性。为了概括这一不确定性，本文引入三角模糊变量来表示实施需求响应后的用户电力需求[13]。其由清晰数构成的三元组表达式为：

Leφ,t=(L1,L2,L3)=(ω1Lφ,t,ω2Lφ,t,ω3Lφ,t)

(5)

式中：Leφ,t为φ相用户t时段实施需求响应后的电力需求的模糊表达式，L1、L2、L3为模糊表达式的隶属度参数，Lφ,t为由式(1)确定的清晰表达式，ω1、ω2、ω3为表征不确定范围的比例系数。上述模糊变量的隶属函数为：

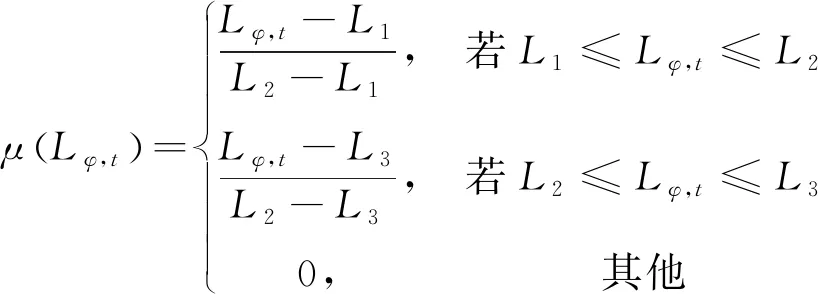
(6)

2 台区三相不平衡优化模型

本文所提三相不平衡治理措施建立在负荷预测的基础上，根据台区A、B、C三相电力用户负荷预测值，通过调整日前各时段电价引导用户改变自身用电行为。在建立三相不平衡优化模型时，需要充分考虑台区整体运行状态，兼顾电力用户用电习惯，因此需要满足以下约束条件：

1) 电价约束。为了避免优化过程中过高、过低电价的出现，维持整个系统的运行稳定性，通过优化确定的各时段日前电价波动范围应限制在初始电价的一定比例范围内。

(7)

式中：αmin、αmax分别为电价允许波动范围的最小、最大值对应的比例系数。

2) 电力用户用电量约束。为了尽可能保证优化前后台区运行的稳定性，优化后的各相用户日总用电量应在原日总用电量的一定范围内。考虑用户参与需求响应的不确定性，本文采用模糊机会约束对优化后的用户日用电量进行限制，使得在满足某一置信度的前提下，用户的日用电量处于给定范围内。

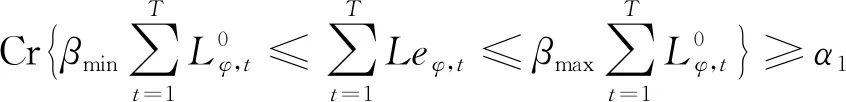
(8)

式中：Cr{·}为置信度表达式；βmin、βmax分别为各相日用电量允许波动范围的最小、最大值对应的比例系数；α1为给定的置信度。

3) 用电量满意度约束。为了充分考虑用户的用电习惯与利益，本文将用户用电量满意度作为三相不平衡治理的约束条件，同样以模糊机会约束的形式给出，如式(9)所示。

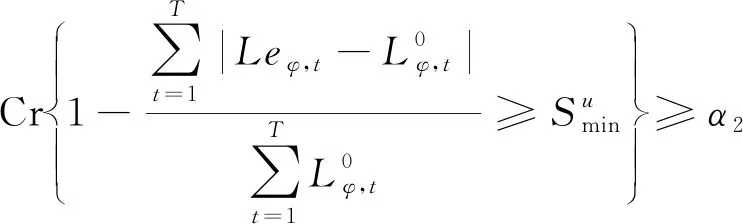
(9)

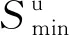
4) 目标函数。本文所解决的问题为降低台区三相不平衡度，因此以24 h内三相负荷用电量期望值与三相用电量期望值的平均值之差的平方和最小为目标。

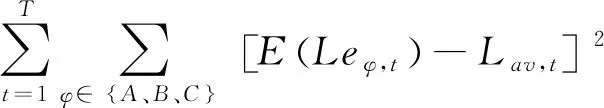
(10)

式中：E(·)为模糊变量期望值计算算子；Lav,t为t时段A、B、C三相用电量期望值的平均值，由式(11)计算得到。

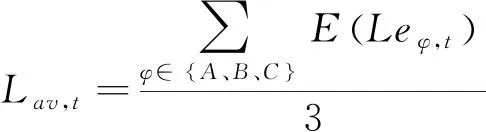
(11)

3 模型求解

式(5)定义了以三角模糊变量表示的优化后的各时段三相电力需求，式(10)为含模糊变量期望值的目标函数。根据三角模糊变量期望值计算公式[14]，可以求得优化后的电力需求期望值为：

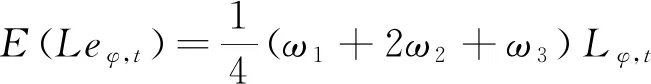
(12)

将式(12)代入式(10)，即可得到对应的确定性表达式。

式(8)-(9)为模糊机会约束表达式，本文采取文献[14]中的清晰等价类方法，将其转化为确定性表达式。

清晰等价类方法适用于形如式(13)的模糊机会约束：

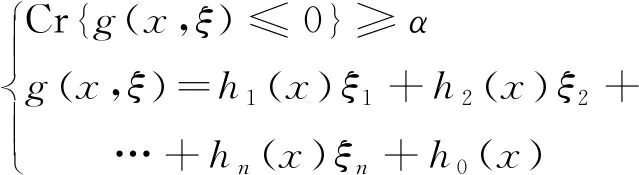
(13)

式中：x为决策变量；ξ为模糊变量集合；α为给定的置信水平；ξk(k=1,2,…,n)为梯形模糊变量，其四元组表达式为(rk1,rk2,rk3,rk4)，当rk2=rk3时，梯形模糊变量退化为三角模糊变量。

上述模糊机会约束的清晰等价形式如式(14)所示。

h0(x)≤0

(14)

其中，h+k(x)、h—k(x)的含义如下：

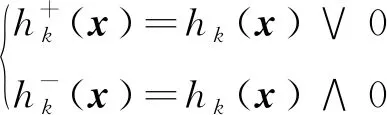
(15)

式中：∨表示取二者中的较大者，∧表示取二者中较小者的相反数。

采用上述方法对式(8)-(9)进行处理，最终得到的确定性约束分别如式(16)-(17)所示。

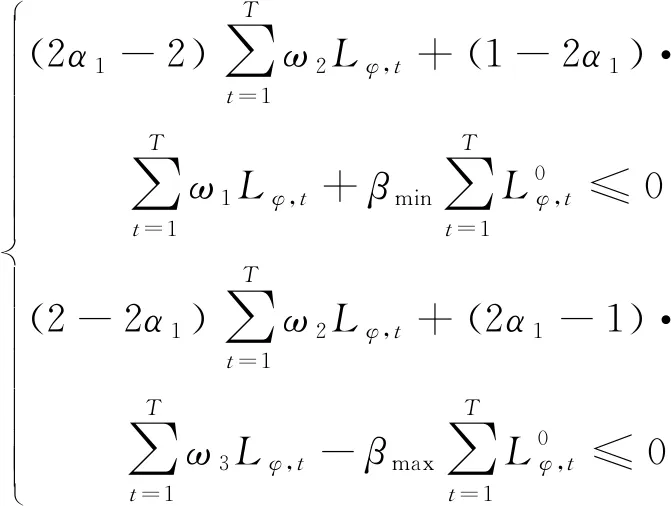
(16)

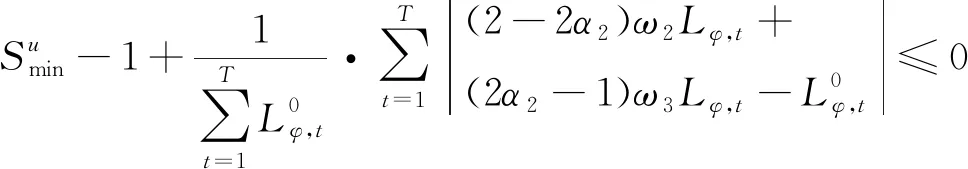
(17)

转化后的优化模型为确定性模型，不含模糊变量，可以采用商业求解器GUROBI进行求解。

4 算例分析

4.1 算例参数

本文以24 h为一个用电周期，将其分为24个时段，每个时段为1 h，图2为某台区典型日三相负荷曲线(即初始电力需求)。

图2 三相初始电力需求

在本文算例中，三相用户初始固定电价均为0.5元/kW·h，需求弹性矩阵系数参考文献[15]，三角模糊变量比例系数ω1、ω2、ω3分别为0.8、1、1.2，各时段电价约束的最大、最小比例系数αmin、αmax分别为0.4、2，日用电量约束比例系数βmin、βmax分别为0.825、1.15，用电量满意度的最小值Su min为0.8，置信水平α1、α2分别为90%、95%。在Matlab R2017b平台上使用YALMIP工具包调用GUROBI求解器对优化模型进行求解。

4.2 算例结果分析

定义三相不平衡度计算公式如式(18)所示，式中ηt为t时段台区三相不平衡度。

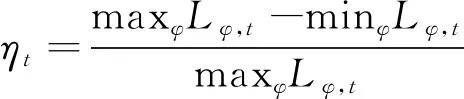
(18)

优化后的三相负荷曲线与按式(18)计算的优化前后三相不平衡度如图3所示，优化后的日前电价如图4所示。

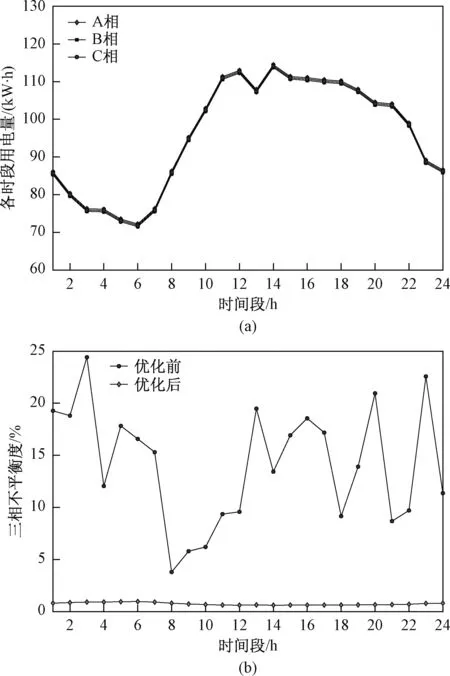
图3 优化后的三相负荷曲线及不平衡度(初始为固定电价)

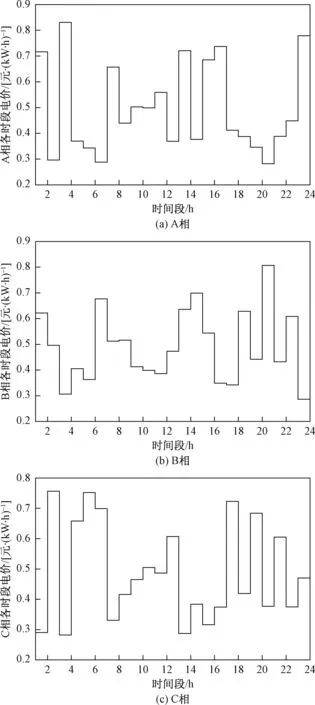
图4 优化后的三相分时电价(初始为固定电价)

由图3可以看出，优化后24 h内各时段三相负荷大小基本相同，三相不平衡度均在1%左右，达到了减小三相不平衡度的目的。通过观察图4中优化后的各相电价可以看出，在每个时段内，对三相不平衡度贡献越大的相，其电价越高，这是由模型的目标函数决定的。进一步分析优化后的电价可以看出，在第2至7个时段(负荷低谷)，部分相别出现电价过高的现象，而在第11至15个时段(负荷高峰)，部分相别则出现电价过低的现象，这些会给台区实际运行造成不利影响，可能导致台区日负荷峰谷差增大。作者认为这是由于仿真算例采用的初始电价为固定电价，电价本身没有体现峰谷用电需求的差异。为了进行对比分析，将算例中的初始电价由固定电价变更为图5所示的分时电价，其他参数不变，再次进行计算，对应优化后的三相负荷曲线与优化前后三相不平衡度、优化后三相分时电价分别如图6、图7所示。

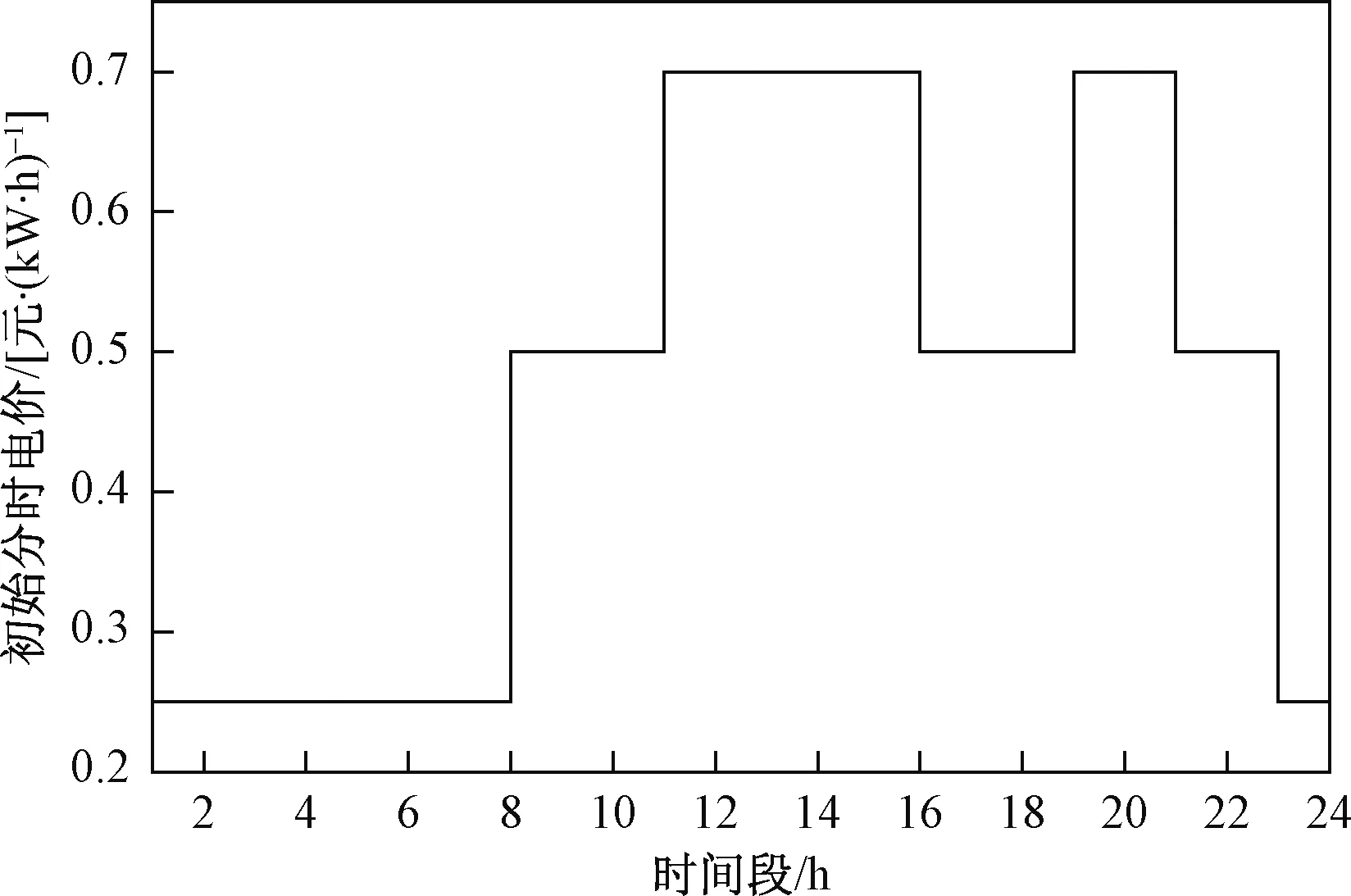
图5 初始分时电价

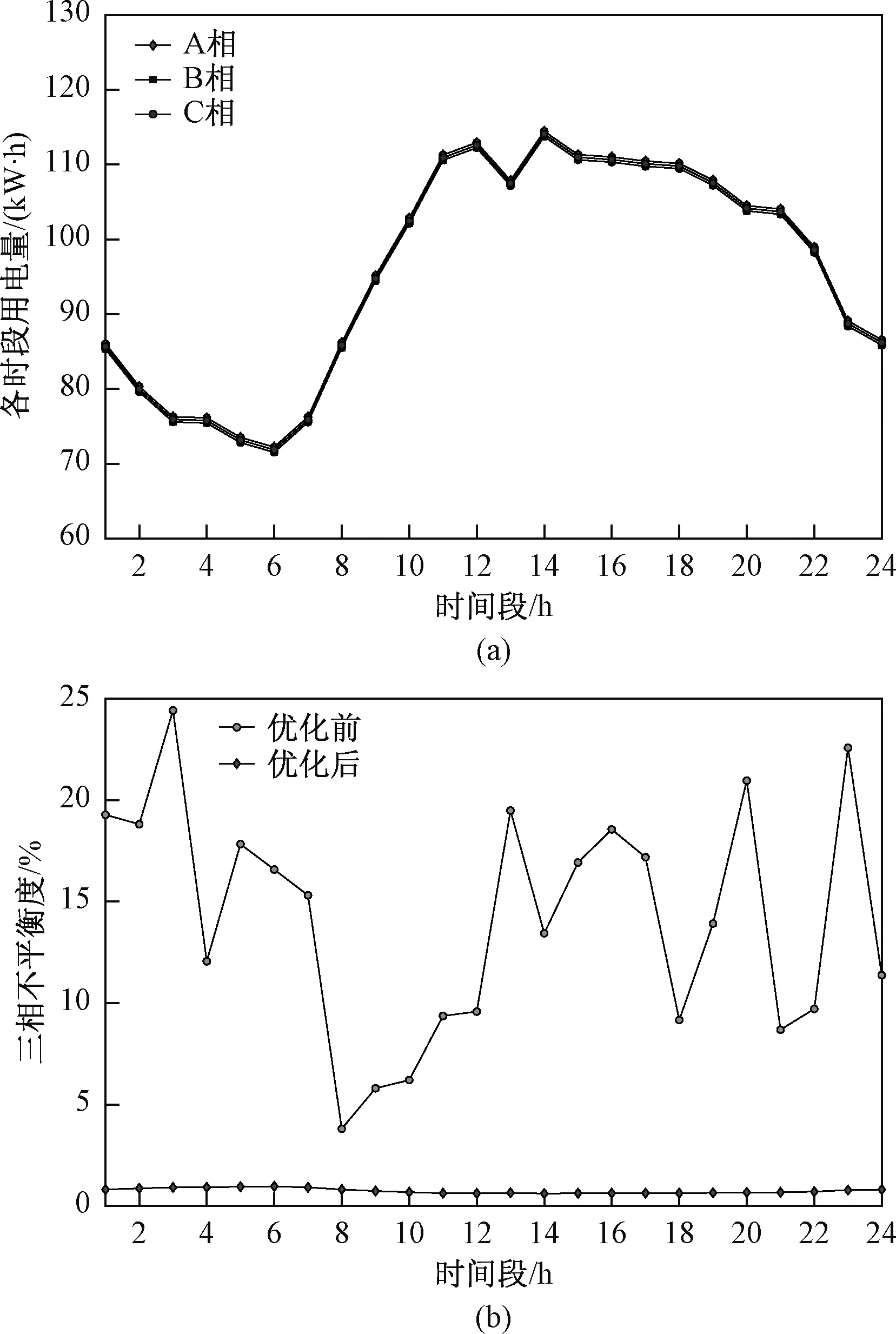
图6 优化后的三相负荷曲线及不平衡度(初始为分时电价)

从优化结果可以看出，初始电价为分时电价时，三相不平衡治理同样取得了较为明显的效果，且避免了固定电价情况下出现的负荷低谷高电价、负荷高峰低电价问题，总体治理效果较好。对初始(未治理)状态、初始电价为固定电价时、初始电价为分时电价时三个场景下的优化结果进行比较，结果如表1所示。

图7 优化后的三相分时电价(初始为分时电价)

表1 不同场景下的三相不平衡优化结果对比

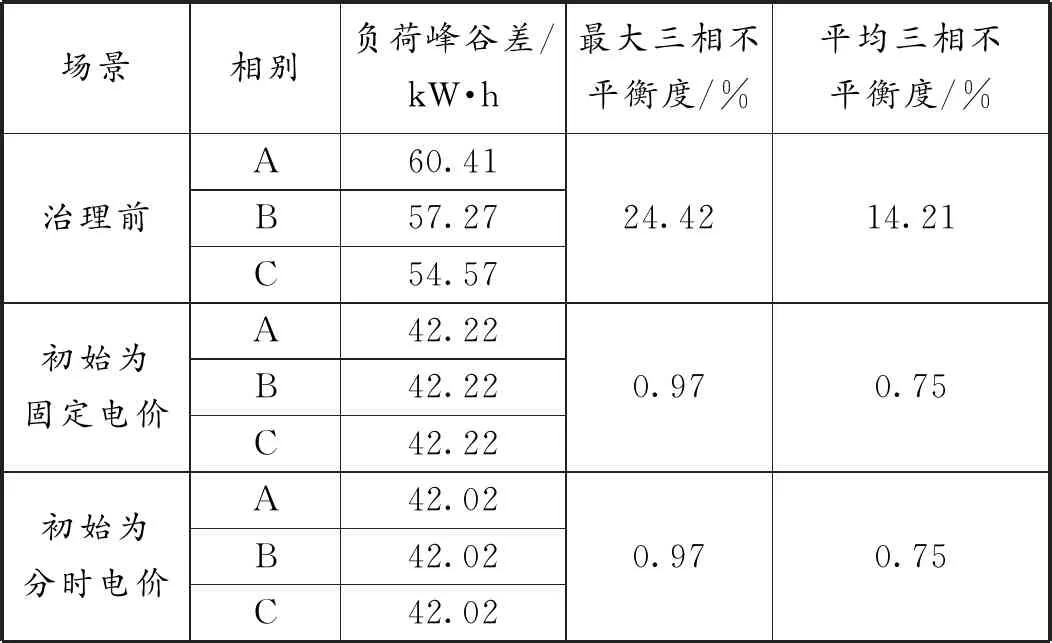
场景相别负荷峰谷差/kW·h最大三相不平衡度/%平均三相不平衡度/%治理前A60.41B57.27C54.5724.4214.21初始为固定电价A42.22B42.22C42.220.970.75初始为分时电价A42.02B42.02C42.020.970.75

由表1可知，本文提出的考虑需求响应及其不确定性的台区三相不平衡治理措施能够有效降低三相不平衡度，提高台区经济运行水平，同时能够减小负荷峰谷差。对于不同电价政策，本文提出的治理措施优化效果不同。初始电价为固定电价时，优化结果存在低谷电价高、高峰电价低的问题，初始电价为分时电价，能够有效避免上述问题，且治理效果稍优于固定电价。为了进一步说明本文所提治理措施的有效性和经济性，按式(19)与式(20)分别计算优化前后各相电力用户的平均用电电价和台区用户总体平均电价，结果如表2所示。

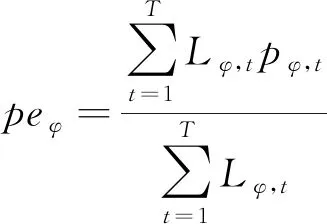
(19)

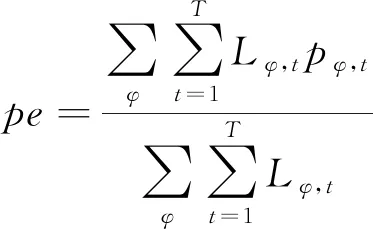
(20)

式中：peφ为φ相用户平均用电电价；pe为台区用户总体平均电价式中：peφ为φ相用户平均用电电价；pe为台区用户总体平均电价。

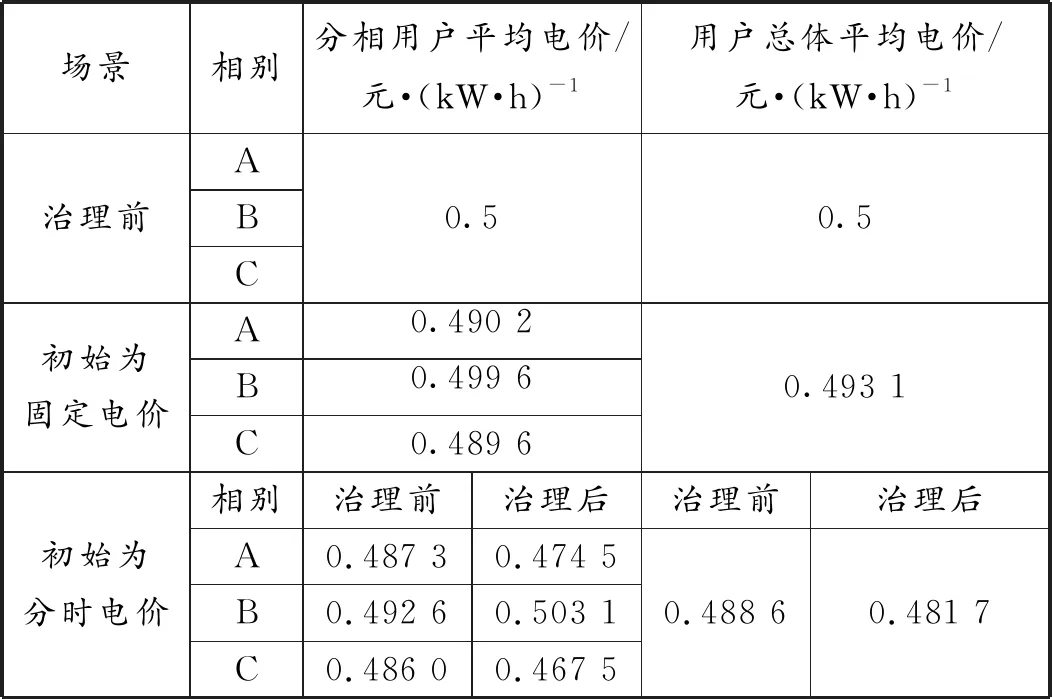
表2 优化前后台区用户平均用电电价对比

从表2可以看出，初始电价为固定电价时，优化后各相用户平均电价均低于初始电价；初始电价为分时电价时，优化后A、C相用户平均电价低于优化前平均电价，B相用户平均电价略高于优化前，但台区用户总体平均电价低于优化前。

5 结论

1)针对低压配电台区日常运行中普遍存在的三相不平衡问题，立足于未来电力市场建设及智能台区发展，提出了基于电价型需求响应的三相不平衡治理措施，为了充分考虑用户参与需求响应的不确定性，利用三角模糊变量建立了PBDR模型。

2)利用清晰等价类方法处理模糊机会约束，将其转化为确定性约束进行求解，大大提高了模型求解效率。

3)算例采用固定电价与分时电价两种初始电价形式，算例结果表明所提出的治理措施在两种电价政策下均能有效改善台区三相运行水平，且分时电价下的治理效果略优于固定电价，能够避免负荷低谷时期高电价与负荷高峰时期低电价问题的出现。

本文提出的台区三相不平衡治理方法对市场及技术发展有一定要求，在现阶段实际应用中存在一定难度，但为目前所面临的问题提供了一种新的解决思路。实际负荷中有相当一部分用电需求缺乏弹性，单靠价格机制应不足以解决三相不平衡问题，这也是今后研究的重点。