模糊神经网络的优化及其应用
李浩楠 刘勇


摘 要:为了提高模糊神经网络的泛化能力和收敛速度,以及减小误差,提出了采用動量梯度下降算法和RMSprop优化算法模糊神经网络的方法,研究并设计神经网络的参数调整的自适应过程,在代价函数中加入正则项,实现参数的更新,同时保证模糊神经网络的收敛速度,对预测输出和实际输出的拟合效果和误差进行比较。将二种优化模糊神经网络的算法应用于非线性函数逼近、Mackey-Glass混沌时间序列和水质等级评价的输出预测中,实验结果表明,RMSprop的预测输出和实际输出的误差和拟合效果优于动量梯度下降算法。
关键词:梯度下降;模糊神经网络;正则化;优化算法
DOI:10.15938/j.jhust.2020.06.021
中图分类号: TP273
文献标志码: A
文章编号: 1007-2683(2020)06-0142-08
Optimization and Application of Fuzzy Neural Network
LI Hao-nan, LIU Yong
(College of Electronic Engineering, Heilongjiang University, Harbin 150080)
Abstract:In order to improve the generalization ability, convergence speed and reduce the error of the fuzzy neural network, the method of using momentum gradient descent algorithm and RMSprop optimization algorithm to optimize the fuzzy neural network is proposed. The adaptive process of parameter adjustment of the neural network is studied and designed. Regular terms are added to the cost function to update the parameters, and the convergence speed of the fuzzy neural network is guaranteed. The fitting effect and error between the predicted output and the actual output are compared. The two optimization algorithms of fuzzy neural network are applied to output prediction of non-linear function approximation, Mackey-Glass chaotic time series and water quality grade evaluation. The experimental results show that the error and fitting effect of RMSprop′s predicted output and actual output are better than that of momentum gradient descent algorithm.
Keywords:gradient descent;fuzzy neural network;regularization;optimization algorithm
0 引 言
模糊神经网络将模糊逻辑系统和人工神经网络相结合,兼有良好的知识表达能力和强大的自学习能力,是神经网络与模糊系统领域重要分支之一[1-2]。将其用于控制领域,如工业控制系统,机器人控制系统、农业控制领域等。乔俊飞等[3]提出了
一种自适应聚类方法建立起网络的结构,赋予各参数的初值,用于水质的检测,得到了理想的效果。朱岩[4]分析了自控温室系统中的气候控制问题,并对温室环境控制系统进行了总体设计。郝琪[5]将神经网络和模糊补偿解耦控制配合使用,实现了温室的智能控制。帅知春等[6]将模糊神经网络用于温室热氧化碳的控制,克服了现有控制方法需要大量的数据传输、准确的数学模型等缺陷。夏江南等[7]将粒子群优化算法引入模糊神经网络中,提高了训练的效率。
上述研究均表明模糊神经网络能够结合多种特征用于控制领域,能够改善传统控制效率低、耗能大、周期长的问题。模糊神经网络利用神经网络对模糊规则进行训练,并将训练得到的模型表示为易于理解的模糊规则。而现有的研究表明,模糊神经网络对控制量的模糊化过程,会造成一定的误差,并包含了大量的模糊规则,降低了模型的可解释性。
针对存在的不足,本文一方面对损失函数进行了改进,同时引入正则化项;另一方面,采取不同的优化算法对模糊神经网络的参数进行优化,实现了模糊神经网络模型结构的自适应调整,从而减小误差,提高模型的可解释性。动量梯度下降法和RMSprop算法是深度学习应用非常广泛的优化算法,尤其是在计算机视觉和文本处理方面,取得了不错的效果,但是在模糊神经网络方面其应用较少,多数情况下,使用的标准梯度下降方法[8-9]。本文将动量(Momentum)梯度下降算法和RMSprop算法引入模糊神经网络,对其优化结果进行对比,并利用其分别对非线性函数逼近、Mackey-Glass混沌时间序列和水质等级评价经典例子进行了参数建模,证明了2种优化算法的有效性和对比性。
1 模糊神经网络的结构及算法
模糊神经网络结构如图1所示,分为5层,包括输入层、模糊化层、规则层、归一层和输出层。
输入层:输入向量为x=[x1,x2,…,xn],各个分量xi分别与网络的该层节点直接相连,Net1i是输入层的输出;
Net1i=u1i=xi,i=1,2,…,n(1)
模糊化层:将输入向量模糊化,其中每个节点代表一个隶属度函数,此处隶属度函数通常取为高斯函数,
Net2ij=uij=exp[(uij-cij)2bij2](2)
式中,i=1,…,n,j=1,…,mi ,n是输入向量的个数,mi是模糊规则数;cij,bij分别是高斯函数的中心和宽度;Net2ij是模糊化层的输出。
规则层:对模糊规则的If条件语句进行描述,模糊神经网络的输出为每条语句的适应度值,Net3h是规则层的输出,即:
Neth3=u1i1·u2i2…unin(3)
式中:ij=1,2,…,mj,h=1,2,…,m,m=∏nj=1mj
归一化:对规则层的输出进行归一化,该层的节点数等于规则层的节点数,其归一化公式为,Net4h是归一化层的输出:
Neth4=Neth3∑mh=1Neth3(4)
输出层:采用重心法实现清晰化和去模糊化处理,所以网络的输出是
yk=Netk5=∑mh=1wkhNeth4=∑mh=1wkhNeth3∑mh=1Neth3(5)
式中:k=1,…,r,r是输出层的节点数;yk是输出层的结果。
在反向传播的过程中,传统经验函数为
e=12(Yk-yk)2(6)
其中Yk为模糊神经网络模型对数据实例的预测值,而yk是实际值。在隶属度函数求解合并中,相似的隶属度函数要合并到同一集合。通过加入正则项Ω,即可以实现隶属度函数和其所在集合尽可能相似,而且使隶属度函数集合数量尽可能少,最后训练得到的模型中的模糊规则也较少[10]。加入正则项的损失函数为
J=e+λ*Ω(7)
Ω=∑ni=1∑mij=1(cij-1)2+∑ni=1∑mij=1bij2(8)
2 优化算法对模糊神经网络的改进
2.1 模糊神经网络后相传播
建立模糊神经网络的结构后,基于梯度下降算法对各参数进行优化学习,从而得到完整的模糊神经网络。标准梯度下降算法存在以下缺点:
1)难以选择合适的学习速率,如果学习速率选择过小会造成网络收敛太慢,但是设得太大可能使得损失函数在最小点周围不断摇摆而永远达不到最小点;
2)在训练开始时设置一个较大的学习率,然后每训练若干个周期后按比例降低学习率,虽然这个方法有一些作用,但是由于降低学习率的周期是人为事先设定的,所以它不能很好地适应数据内在的规律;
3)难以逃脱鞍点,鞍点既不是最大点也不是最小点,在这个点附近,所有方向上的梯度都接近于0,标准梯度下降算法很难逃离它[11]。
动量梯度下降法和RMSprop优化算法均是在标准梯度下降法基础上发展出的优化算法。
利用梯度下降法进行误差反向传播计算Ewkh,Ecij,Ebij[12-13]。
Ewkh=-δk5·Neth4(9)
δh4=∑rk=1δk5·wkh(10)
δh3=δh4·∑s=1s≠hNeth3(∑mh=1Neth3)2(11)
δij2=δh3·sij·e(xi-cij)2bij2(12)
当uji是第k个规则的最小值时,sij=1,否则,sij=0。
Ecij=-δij2·2(xi-cij)bij(13)
Ebij=-δij2·2(xi-cij)2bij3(14)
標准梯度下降算法中,代入式(10)~(12),模糊神经网络的参数调整为:
wkh=wkh-α·Ewkh(15)
cij=cij-α·Ecij(16)
bij=bij-α·Ebij(17)
动量梯度下降法基本思想是计算梯度的指数加权平均数,并利用梯度来更新权重。采用动量梯度下降法对参数更新原理如下,β1是动量系数,一般为0.9,β*V是动量项,V表示为本次的梯度下降量(1-V)*dc与部分上次更新量的矢量和,再乘以学习衰减率α,便为参数更新量,与当前的变量值c、b、w相加,得到下一步的变量值:
Vdc=β1*Vdc+(1-Vdc)*dc(18)
Vdb=β1*Vdb+(1-Vdb)*db(19)
Vdw=β1*Vdw+(1-Vdw)*dw(20)
c=c+α*Vdc(21)
b=b+α*Vdb(22)
w=w+α*Vdw(23)
在上面公式中,将损失函数想象为一个碗状,从顶部往下滚球,其中微分项dw,db是为球提供加速度,动量Vdw、Vdb是速度。小球在向下滚动时,由于有加速度存在,使得速度会很快,但是存在β1 小于1,可以认为是摩擦力,所以小球不会无限加速,这便是动量梯度下降法的本质。
为了进一步优化损失函数在更新中存在摆动幅度过大的问题,并且进一步加快函数的收敛速度,RSMprop算法对c、b、w使用了微分平方加权平均数。采用RSMprop优化算法对参数更新如下公式:
Sdc=β2*Sdc+(1-β2)*dc2(24)
Sdb=β2*Sdb+(1-β2)*db2(25)
Sdw=β2*Sdw+(1-β2)*dw2(26)
c=c+α*dcSdc+ε(27)
b=b+α*dbSdb+ε(28)
w=w+α*dwSdw+ε(29)
在上述的公式中Sdc、Sdb和Sdw分别是损失函数在前t-1轮迭代过程中累积的梯度动量,β2是梯度累积的一个指数。所不同的是,RMSProp算法对梯度计算了微分平方加权平均数,然后使用平方根进行梯度更新。这种做法用来修正摆动幅度,消除摆动幅度过大的方向,使得各个维度的摆动幅度都基本一致。另一方面也使得网络函数收敛更快。为了防止分母为零,使用了一个很小的数值ε来进行平滑,一般取值为10-8。
在动量梯度下降和RMSprop梯度下降中的dc=Ec、db=Eb、dw=Ew,在高等数学它们是近似关系。
2.2 优化的模糊神经网络具体流程
为评定模糊神经网络的性能,采用均方根误差(root mean squared error,RMSE)作为其评定指标:
RMSE=∑rk=1J2r(30)
根据以上对模糊神经网络参数的学习,其具体流程为以下4步。
步骤1 初始化参数。学习率α=0.09,动量梯度下降中β1=0.9,RMSprop梯度下降中β2=0.999,隶属度函数中心c、宽度b,输出层权值。
步骤2 在模糊神经网络的训练阶段,由式(1)~(5)计算出输出值yk,式(8)算出正则项。式(9)~(17)为梯度下降过程,从而得到参数变化量(即一阶导数)。
步骤3 式(9)~(17)是标准梯度下降计算参数的更新值;式(18)~(23)是动量梯度下降计算参数的更新值;式(24)~(29)是RMSprop梯度下降计算参数的更新值。
步驟4 判断误差是否满足条件或是否满足最大迭代数,若满足则停止计算,否则,跳转到步骤2继续执行步骤。
3 仿真实验
为验证2种梯度下降算法对模糊神经网络的参数模型的优化能力,将其应用于污水处理过程关键水质参数预测和Mackey-Glass混沌时间序列预测经典案例中,以及非线性函数的逼近中,在测试误差和收敛速度方面,将优化后的模糊神经网络与他人优化算法进行对比。
3.1 非线性函数的逼近
选取式(31)给出的非线性函数:
y=0.6sin(πx)+0.3sin(3πx)(31)
式中x∈[-1,1],在该定义域内随机产生200组数据,其中100组数据作为训练数据,另外100组数据作为测试数据,分别利用动量梯度下降和RMSprop对模糊神经网络进行优化逼近。仿真结果如图2~5所示。
图2为两种优化算法对非线性函数RMSE迭代的结果,随着迭代次数的增加,RMSE的值趋向于零,但是RMSProp的起始值远小于动量梯度下降。图3为动量梯度下降优化的预测输出与实际输出的拟合程度,可以看出,在前一部分样本里其拟合效果非常差,后一部分的拟合效果相对较好。图4为RMSprop优化算法的预测输出和实际输出的拟合程度,由图可以看出,二者的拟合效果好于动量梯度下降的优化。图5为动量梯度下降和RMSprop优化模糊神经网络得预测输出和实际输出之间的误差,RMSprop优化算法的误差分布在零的附近,且小于0.03,而动量梯度下降的误差比较大,即便是后一部分的误差较小,但是也大于RMSprop优化后的误差。所以,可以得出RMSprop更适合优化模糊神经网络。
3.2 Mackey-Glass混沌时间序列
Mackey-Glass混沌时间序列模型:
x(t+1)=1+ax(t-τ)1+x10(t-τ)-bx(t)(32)
其中a=0.2,b=0.1,τ=17,x的初始向量为x0=0.1,选择250组样本作为训练样本,250组样本作为测试样本。
仿真结果如图6~9所示,图6为动量梯度下降法和RSMprop优化算法对Mackey-Glass混沌时间序列训练的RMSE,在其他条件一致的情况下,RSMprop的收敛速度和动量梯度下降相差不多,甚至在10代以前,RSMprop的收敛速度更快,而且RSMprop由更小的误差开始迭代下降。图7和图8分别为动量梯度下降的输出和实际输出的拟合图与RSMprop优化算法的输出与实际输出的拟合图,由图可以看出动量梯度下降的拟合效果较差,而RSMprop的拟合效果较好。图9为动量梯度下降和RMSprop的误差对比图,动量梯度下降的误差远远大于RMSprop。
表1为基于不同网络对Mackey-Glass时间序列的训练RMSE结果。对比试验选取基于支持向量回归的局部递归模糊神经网络(locally recurrent fuzzy neuralnetwork with support vector regression,LRFNN-SVR)[14]、基于功能链接的文化协同粒子群模糊神经网络(functional-link-based neural fuzzy net-work with cultural cooperative particle swarmoptimization,FLNFN-CCPSO)[15]、快速在线自组织简约模糊神经网络(fast and accurate online self-organizing scheme for parsimonious fuzzy neu-ral networks,FAOS-PFNN)[16]、基于小波变换-模糊马尔科夫链算法的递归模糊神经网络(wavelettransform fuzzy markov chain RFNN,WTFMC-RFNN)[17]和递归模糊神经网络(recurrent fuzzy neural network,RFNN)进行了比较,可以看出RMSprop的均方差更小、更加适用于对模糊神经网络的梯度下降。
3.3 水质评价模型
将动量梯度下降和RMSprop优化后的模糊神经网络模型应用于经典的水质评价模型,在matlab中进行仿真。
仿真结果如图10~13所示。图10为水质评价模糊的训练样本RMSE的迭代效果,动量梯度下降优化算法随着迭代次数的增加基本保持稳定,甚至略有下降,且绝对值在增加。RMSprop优化算法随着迭代逐渐趋于零,其迭代效果好于动量梯度下降算法。图11为动量梯度下降的预测输出与实际输出的拟合图,由图可以看出,其拟合效果比较差。图12为RMSprop优化的预测输出和实际输出的拟合情况,拟合效果远好于动量梯度下降算法。图13为两种优化算法的预测输出和实际输出的误差对比,动量梯度下降优化模糊神经网络的误差比较大,而RMSprop优化的误差远小于动量梯度下降,更适合优化模糊神经网络。
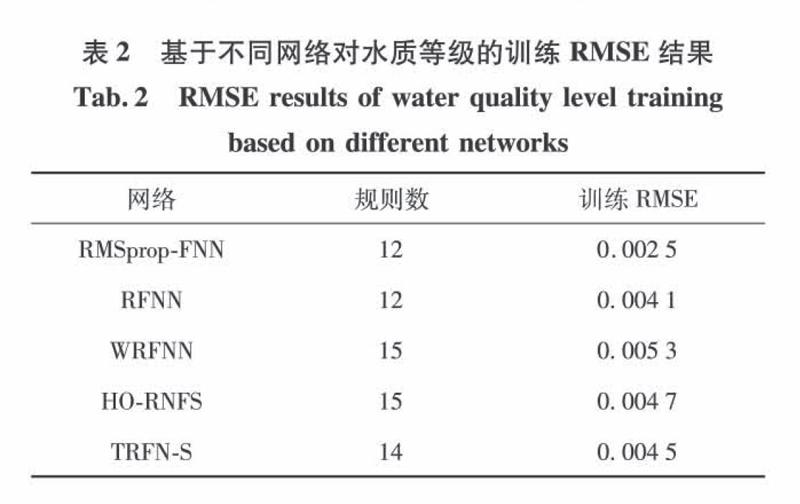
表2为基于不同网络对水质等级的训练RMSE结果,对比试验选取了递归模糊神经网络(recurrent fuzzy neural network,RFNN)、小波变换递归模糊神经网络(wavelet-based recurrent fuzzy neural network,WRFNN)[18]、高阶递归神经模糊系统(high-order recurrent neuro-fuzzy system,HO-RNFS)[19]、有监督学习的TSK型 递归 模 糊 网 络(TSK-type recurrent fuzzy net-work with supervised learning,TRFN-S)[20],可以发现基于RMSprop优化算法的精度更高,更适合模糊神经网络的梯度优化。
4 结 论
为了提高模糊神经网络的收敛速度和泛化能力,本文提出了将动量梯度下降和RMSprop优化算法应用到模糊神经網络中,在保证收敛速度的前提下,对参数进行调整,提高神经网络的自适应能力。通过非线性函数逼近、Mackey-Glass混沌时间序列和水质等级评价的建模,对动量梯度下降和RMSprop的拟合程度、预测输出与实际输出之间的误差进行仿真输出,得到下面的结论:
1)提出了利用动量梯度下降和RMSprop对模糊神经网络进行参数优化。
2)相对动量梯度下降,RMSprop优化算法的拟合效果更好,误差更小,更适合对模糊神经网络进行优化,同时证明了网络的有效性。
参考文献:
[1] 乔俊飞,丁海旭,李文静.基于WTFMC算法的递归模糊神经网络结构设计[J/OL].自动化学报:1-12[2019-10-11].https://doi.org/10.16383/j.aas.c180847.
QIAO Junfei, DING Haixun, LI Wenjing.Structure Design of Recurrent Fuzzy Neural Network Based onWTFMC Algorithm[J/OL].Acta Automatica Sinica:1-12[2019-10-11].https://doi.org/10.16383/j.aas.c180847.
[2] 武俊峰,艾岭.一种基于改进聚类算法的模糊模型辨识[J].哈尔滨理工大学学报,2010,15(3):1.
WU Junfei, AI Ling. Fuzzy Model Identification Based on Improved Clustering Algorithm[J]. Journal of Harbin University of Science and Technology,2010,15(3):1.
[3] 乔俊飞,王会东.模糊神经网络的结构自组织算法及应用[J].控制理论与应用,2008(4):703.
QIAO Junfei, WANG Huidong. Structure Self Organizing Algorithm of Fuzzy Neural Network and Its Application[J].Control Theory & Applications,2008(4):703.
[4] 朱岩. 基于模糊神经网络的温室自动控制研究[D].天津:河北工业大学,2005.
[5] 郝琪. 智能温室远程控制系统研究与设计[D].秦皇岛:燕山大学,2011.
[6] 帅知春,林伟.基于模糊神经网络的温室二氧化碳控制[J].现代计算机,2006(9):7.
SUAI Zhichun,LIN Wei.Greenhouse Carbon Dioxide Control Based on Fuzzy Neural Network[J].Modern Computer,2006(9):7.
[7] 夏江南,王杜娟,王延章,等.基于结构自适应模糊神经网络的前列腺癌诊断方法[J].系统工程理论与实践,2018,38(5):1331.
XIA Jiangnan,WANG Dujuan,WANG Yanzhang,et al. Prostate Cancer Diagnosis Method Based on Structure Adaptive Fuzzy Neural Network[J].Systems Engineering-Theory & Practice,2018,38(5):1331.
[8] 邓子云.基于有动量和自适应lr梯度下降法BP神经网络的城市用电量预测技术[J].江苏科技信息,2018,35(3):32.
DEGN Ziyun. Urban Electricity Consumption Forecasting Technology Based on Momentum and Adaptive LR Gradient Descent BP Neural Network[J]. Jiangsu Science & Technology Information,2018,35(3):32.
[9] 沈卉卉,李宏伟.基于动量方法的受限玻尔兹曼机的一种有效算法[J].电子学报,2019,47(1):176.
SHEN Huihui,LI Hongwei. An Efficient Algorithm for Constrained Boltzmann Machine Based on Momentum Method[J]. Acta Electronica Sinica,2019,47(1):176.
[10]黄磊,杜昌顺.融合群稀疏与排他性稀疏正则项的神经网络压缩情感分析方法[J].北京化工大学学报(自然科学版),2019,46(2):103.
HUANG Lei, DU Changshun. Neural Network Compressed Sentiment Analysis Method Combining Group Sparsity and Exclusive Sparse Regularities[J]. Journal of Beijing University of Chemical Technology(Natural Science Edition),2019,46(2):103.
[11]沈海龙,赵颖,邵新慧.一种求解鞍点问题的PGSS方法[J].东北师大学报(自然科学版),2019,51(3):46.
SHEN Hailong,ZHAO Ying,SHAO Xinhui. A PGSS Method for Solving Saddle Point Problem[J]. Journal of Northeast Normal University(Natural Science Edition),2019,51(3):46.
[12]常永虎,李虎阳.基于梯度的优化算法研究[J].现代计算机,2019(17):3.
CHANG Yonghu,LI Huyang. Research on Gradient Based Optimization Algorithm[J]. Modern Computer,2019(17):3.
[13]彭章友,夏海琴.无源雷达目标跟踪的线性回归-梯度下降算法[J].电子测量技术,2019,42(15):1.
PENG Zhangyou,XIA Haiqin. Linear Regression Gradient Descent Algorithm for Passive Radar Target Tracking[J]. Electronic Measurement Technology,2019,42(15):1.
[14]LIN C J, CHEN C H, LIN C T. AHybrid of Cooperative Particle Swarm Optimization and Cultural Algorithm for Neural Fuzzy Networks and Its Prediction Applications[J]. IEEE Transactionson Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(1):55.
[15]WANG N, ER M J, MENG X. A Fast AndAccurate Online Self-Organizing Scheme for Parsimonious Fuzzy Neural Networks[J].Neurocomputing, 2009, 72(16/18):3818.
[16]孫冬璞,谭洁琼.一种快速全局中心模糊聚类方法[J].哈尔滨理工大学学报,2019,24(4):110.
SUN Dongpu,TAN Jieqiong. A Fast Global Center Fuzzy Clustering Method[J]. Journal of Harbin University of Science and Technology,2019,24(4):110.
[17]LIN C J, CHIN C C. Prediction and Identification Using Wavelet-Based Recurrent Fuzzy Neural Networks[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cyber-netics), 2004, 34(5):2144.
[18]THEOCHARIS J B. A Highorder Recurrent Neurofuzzy System With Internal Dynamics:Application to the Adap-Tive Noise Cancellation[J]. Fuzzy Sets and Systems, 2006,157(4):471.
[19]JUANG C F. A TSK-typeRecurrent Fuzzy Network for Dynamic Systems Processing By Neural Network and Genetic Algorithms[J]. Fuzzy Systems IEEE Transactions on, 2002,10(2):155.
[20]JUANG C F, HSIEH C D. A Locally RecurrentFuzzy Neural Network with Support Vector Regression for Dynamic System Modeling[J]. IEEE Transactions on Fuzzy Systems,2010, 18(2):261.
(编辑:温泽宇)
收稿日期: 2019-05-07
基金项目: 国家自然科学基金(61501176);黑龙江省自然科学基金(F2018025).
作者简介:
李浩楠(1994—),男,硕士研究生.
通信作者:
刘 勇(1970—),男,副教授,硕士研究生导师,E-mail:liuyong@hlju.edu.cn.

