基于汊点水位预测校正的闸控河网水动力模拟

王文杰，张晓波，王 攀

（浙江省水利水电勘测设计院，浙江 杭州 310002）

1 问题的提出

平原河网水动力数值模拟广泛应用于平原地区防洪排涝、生态调度、水环境整治等诸多水利工作，是水利规划设计的重要研究手段。河网水动力数值模拟的原理是求解离散化的圣维南方程组，但由于系数矩阵的稀疏非带状特征，直接求解河网整体离散方程组往往耗时较长，已无法满足智慧水利等相关工作对模拟速度、精度的高要求。因此，目前主流思路是对河网进行分级求解，如通过特殊的河道（汊点）编码，把河网系数矩阵转换为类似单一河道的带状矩阵进行求解[1-3]，或先将河道首末断面变量与汊点连接条件及边界条件联合建立整体矩阵，得解后再反推河道内各断面水力要素值[4-5]。但无论是哪种方法，在断面数较多、初始误差较大时都存在误差累计效应，若首末断面变量关系存在失真，也极易导致求解计算崩溃。为此，近年来有学者提出汊点水位预测 — 校正法[6]，主要思路是利用河网汊点回水效应，建立汊点处水位校正量与流量的关系，先对未知时层的汊点水位进行迭代收敛，求得汊点水位后再反推汊点间内河道各断面水力要素值，由于无需建立和求解整理连接矩阵，因此能有效避免分级解法中出现的各种不稳定现象。围绕该方法，不少学者又相继开展水流 — 水质耦合模型、一二维河湖系统耦合模型等研究，丰富了该方法的应用场景[7-8]。

但是，当河网内建有水闸、泵站等控制性泄水建筑物时，由于含闸河道水流连续状态被破坏，通过求解非线性离散方程回推进汊流量的方法失效，导致有关汊点水位无法像普通河道一样直接迭代校正。针对该问题，朱德军等提出2点改进[9]：一是建筑物局部为缓流时，可近似处理成局部水头损失；二是将建筑物视为连接上下游河道的特殊汊点，与普通汊点一起参与计算，并在迭代步中不断修正建筑物下游水位直至满足流量守恒条件。但在实际应用中，上述改进均存在一定局限，如局部水头损失的量化十分复杂，且计算精度无法保证；作为特殊汊点参与计算则仅适用于局部流态为急流的情况，且需要事先明确建筑物上游侧的边界条件。由于平原河网水位相差有限，泄水建筑物局部多以堰流为主，其过流能力通常与上、下游水位相关，有的甚至没有固定的水流流向，以上改进均难以应用于存在较多闸站工程的平原河网水动力模拟中，限制了推广范围。

针对以上缺陷，本文以平原河网最为常见的平底式闸门为例，引入闸门不同流态过流流量公式作为建筑物与上下游河道的连接条件，通过建立上下游河道与水闸过流条件联合方程并求解，可有效解决原方法中含泄水建筑物河道进汊流量无法推求的问题，且对泄水建筑物的控制形式可根据实际调度需要灵活设置，使汊点水位预测校正法能够有效地应用于含较多控制性闸站的平原缓流河网水动力模拟中，拓展该方法的应用范围。本文以浙江省温黄平原河网为例，验证该方法的可行性和稳定性，分析模型的计算效率。

2 汊点水位预测 — 校正法

树状或环状河网的基本单元可视为由汊点和河段组成（见图1）的结构，其中汊点表现为不同河段的交接点或边界条件。当河网水动力过程由一维圣维南方程组描述时，对于包含n个断面的河段，每个未知时层均可联立2（n -1）个方程式，但未知水力要素有2n个（Z1，Q1，…Zn，Qn），因此若给定两端汊点处未知时层水位，则齐次方程组成立，河段未知时层全部水力要素得解。汊点水位预测校正法的思路便是通过不断的预测 — 校正 — 迭代过程，优先求解汊点处未知时层水位，再反推至河段内各断面。其求解流程如下（假设T时刻全部水力要素已知，欲求T+1时刻要素值）。

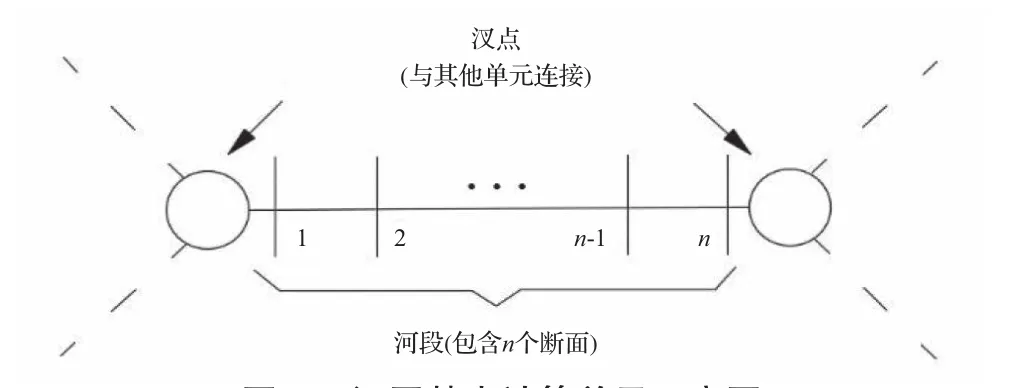
图1 河网基本计算单元示意图

（1）以T时刻水位作为各汊点的初始迭代水位，代入河段方程组中求得各断面该预测水位下的水力要素值。朱德军等提出可采用Newton - Raphson 法求解形成的非线性方程组[5]。本文建议在河段不包含控制闸站时，采用追赶系数法进行求解，即：

对于首末断面：

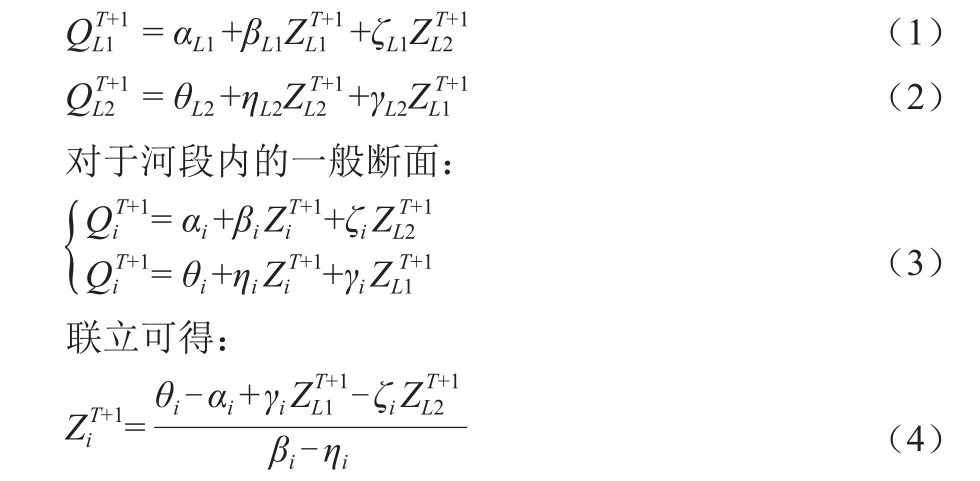
（2）提取计算结果中每一河汊的进出流量值，并计算对应汊点水位校正值Δh，计算公式为：

式中：Qi、Ai、Bi分别为流入汊点断面的流量（m3/s）、过流面积（m2）和面宽（m）；Qo、Ao、Bo分别为流出汊点断面的流量、过流面积和面宽；α为近似系数，一般取1.0 ～2.0[4]。可以证明Δh具有稳定的收敛性。

（3）若Δh小于预设容差（一般取0.005 ～ 0.010 m），则认为当前汊点满足汊点连接条件，水位无需修正，否则继续校正汊点水位：+Δh，并以作为下一迭代步的汊点水位代入河段方程组进行计算。

（4）若某迭代步中所有汊点均能满足汊点连接条件，则认为该状态下的汊点水位组合符合实际，并以该状态下各断面的水力要素值作为T+1时刻的要素值。

（5）依次逐时段推求，直至计算结束。

可以看出，该方法的求解思路类似于分级解法，即通过分步求解河汊和河道2部分的水力要素值，避免面对大型稀疏系数矩阵，从而降低方程组求解的复杂性，提高模型计算速度。但区别于传统分级解法，该方法在构建模型时不用区分干支流、无需优化汊点编码结构，因此具有较强的灵活性和易于模块化编程的特点，且在每个迭代步推求河汊进出流量时，有条件实现多单元并行计算，进一步提升模型响应速度，在大规模河网模拟中具有较好的应用前景。根据对温黄平原实例的测试验证，相比传统三级解法，该方法在同等计算条件下完成时长可减少34%，效率提升较为显著。

3 平原含闸河道的处理

当河段包含闸（泵）等建筑物时，虽然闸室局部水流流态复杂，但建筑物前后河道仍满足缓流条件。若设想一个包含闸（泵）建筑物的河道单元，由建筑物、上游河段、下游河段及两端汊点组成，并记2河段首末断面分别为l1、l2、l3、l4（见图2），则根据式（1）及式（2），可建立关系：

图2 含闸河道单元示意图

当采用汊点水位预测校正法时，上述方程仅汊点处水位Zl1、Zl4已知，因此无法直接求解河段各断面水位、流量值。但是，建筑物处通常满足流量连续条件，即Ql1= Ql3，且根据闸门过流经验公式，该流量一般是闸门上下游水位的单值或多值函数，即满足Ql1= Ql3= f闸( Zl2)或Ql2= Ql3=f闸（Zl2，Zl3）。若将该连接条件与式（6）、式（7）联立，则可构建河段未知量的齐次方程组。

本文以平原河网最为常见的平底闸门为例，分别引入堰流和孔流2种不同流态过流经验公式作为建筑物处的连接条件，基本涵盖平原水闸的常见调度场景，使得在已知汊点水位条件下，含闸河道单元内各项水力要素可解。

3.1 堰流状态

对于平原平底闸门，当闸门启出水面，不影响闸坝泄流量时的水流状态为堰流，一般以闸门开启高度与堰上水头的比值大于0.65作为判别条件。在堰流状态下，根据闸上下游水位关系又可分为自由出流和淹没出流2种流态，其中自由出流时闸下水流对泄流能力影响较小，淹没出流需要考虑闸下水流的顶托影响，因此2种流态的求解方法存在显著区别。

3.1.1 自由出流

根据SL 265 — 2016《水闸设计规范》[11]，当堰流流态为自由出流时，过闸流量仅与闸上水头有关，对于平原缓流河网，若忽略闸上行近流速，其过流能力公式为（以图2为例，下同）：

式中：ε为侧收缩系数；m为流量系数；b为水闸总净宽（m）；d为闸底板高程（m）；g为重力加速度，可采用9.81 m/s2。

令Hl2= Zl2-d，并将式（8）与式（6）联立，可以得到Hl2的一元函数。整理后函数形式为：

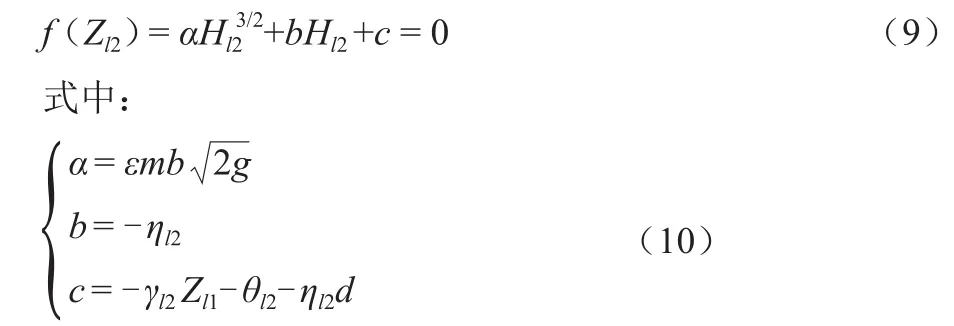
由于追赶系数ηl2＜0恒成立且Hl2＞0，因此可证函数系数b＞0、c＞0，则式（9）在Hl2∈（0,∞）范围内有且仅有唯一解，因此可采用牛顿迭代法得解。已知Hl2后，分别代入式（6）～（8），并考虑Ql2= Ql3，即可解得闸上水位Zl2和闸下水位Zl3。

3.1.2 淹没出流

根据SL 265 — 2016《水闸设计规范》，一般当上下游水头比（Zl3-d）/（Zl2-d）≥0.9时认为水闸流态为淹没出流，此时过流流量与闸上下游水位均有关系。平原河网水级相差有限，因此淹没出流在闸站运行工况中较为常见。《水闸设计规范》中推荐平底闸门淹没出流流量采用下式计算：

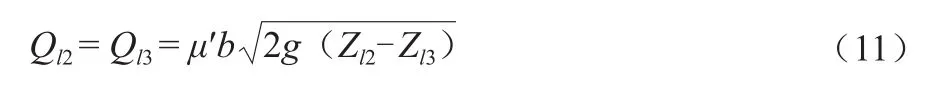
式中：μ′为淹没出流综合流量系数，可采用下式计算，当计算时间步长较小时，前后时刻水位变化有限，Zl2、Zl3可取前一时刻计算成果代替；其余符号意义同前：

已知追赶系数ηl2＜0、βl3＞0，因此有m-m′＜0，又根据式（6）和式（7）可以证得n-n′＜0，则式（15）在（Zl2-Zl3）∈（0,∞）范围内有且仅有唯一解。采用牛顿迭代法求得（Zl2-Zl3）后，代入式（13）即可分别求得闸上下游水位值，回代河段追赶方程则单元内所有未知水力要素得解。

3.2 孔流状态

当闸门门板对过闸水流有不可忽视的阻挡影响时的水流状态为孔流，可采用闸门开启高度与堰上水头的比值小于0.65作为判别条件。根据《水闸设计规范》，当忽略闸上行近流速时，孔流状态下自由出流和淹没出流流态时的过闸流量均可采用下式计算：

式中：σ为孔流淹没系数，μ为孔流流量系数，均可查表或根据经验公式确定；he为孔高（m）。各参数单位与堰流自由出流时类似，令Hl2= Zl2-d，并将式（16）与式（6）联立，可得到Hl2的一元函数。整理后函数形式为：

同理，可证式（17）在Hl2∈（0,∞）范围内有且仅有唯一解，因此可采用牛顿迭代法得解。已知Hl2后，分别代入式（6）、式（7）和式（16），并考虑Ql2= Ql3，即可解得闸上水位Zl2和闸下水位Zl3。

此外，闸门关闭或启用泵站是已知建筑物处流量的特殊情况。当闸门关闭时，有Ql2= Ql3= 0；当启用泵站时，有Ql2= Ql3= q，其中q为泵站当前时刻提水流量。将上述关系代入式（6）和式（7）则方程得解。采用以上方法基本可处理平原平底式水闸运行中的各类工况，在实际模拟中，可先根据上一时刻闸门上下游水位或调度指令判断当前时刻过流状态，再根据堰流或孔流选取对应的推求方程进行求解。此外，由于堰流淹没出流和孔流的流量系数公式中均采用上一时刻水位作为本时刻水位的替代，因此需注意替代成立条件，时间步长的选取不宜过大，避免在流量系数中引入较大误差。

4 应用实例

为了进一步分析论证以上方法的可行性，将上述方法用于浙江省温黄平原河网水动力数值模拟。温黄平原位于浙江省台州市，北临椒江、东部南部面海，域内人口经济集聚，是浙江省重点治涝区域。为分隔水级和抵御外潮，在其河网内部和排海出口处建有众多节制闸站，部分闸站处规划新建排涝泵站，是较为理想的分析对象。2013年“菲特”台风期间，平原发生严重内涝，是近年来发生的较为典型的洪涝灾害，且站点实测资料完整，因此选取该场次洪水过程对模拟结果进行验证。

模型共概化有313个汊点、1 370个断面、42个边界，模拟100座节制闸站，由模型根据其上下游水位关系和设定的闸站控制水位自主调度。河道糙率和计算时间步长均在正常范围内取值。模型河网网络概化见图3。计算所得各代表断面水位过程与实测结果对比见图4。

其中，岩头闸为外海挡潮闸，闸下即为潮位边界，需根据潮位涨落控制开关调度，金清闸为内河节制闸，洪水期间闸门全开泄洪。由计算结果可以看出，2种闸门类型计算水位过程与实测过程均拟合良好，最高水位差值在0.02 m以下，说明模型对闸门过流过程的模拟符合实际。桐屿站、温岭站均为平原内部控制站点，由结果可见，模型在不同洪水阶段、不同来水条件下均能获得良好的模拟效果，体现了上述方法的稳定性。

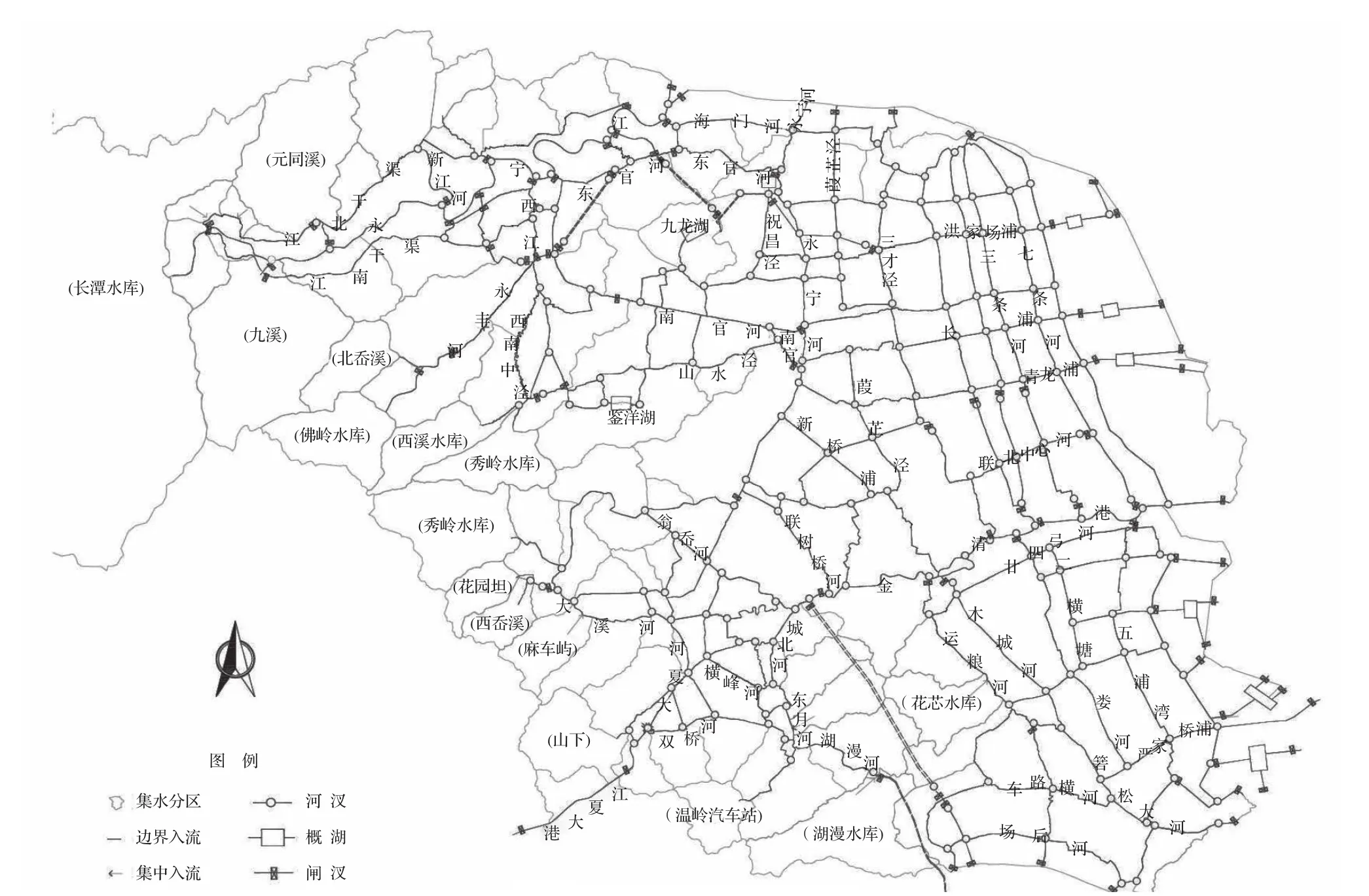
图3 温黄平原河网概化示意图

图4 温黄平原“菲特”台风期间验证水位过程图

5 结 语

（1）汊点水位预测校正法在确保模拟精度的前提下，具有通用性好，计算效率高，易于编程实现等突出优势，在大型复杂河网水动力数值模拟中有较强的应用价值，但原方法及现有改进对含泄水建筑物河网的模拟仍存在不足，难以实际应用。

（2）引入闸门过流能力公式作为建筑物与前后河道的连接条件，通过联立闸门过流能力方程和前后河道的追赶方程，并将方程组转化为关于闸前后水力要素的一元函数，可解决原方法中含闸河段进汊流量无法直接内推的问题，使原方法在大型复杂闸控河网中的应用成为可能，拓展了该方法的应用场景。

（3）以温黄平原“菲特”台风期间洪水过程为例进行实例验证。结果表明，该改进可良好模拟平原不同调度规则下的泄水建筑物，具备可行性和稳定性，且模拟误差满足水动力模拟精度要求。

（4）后续可结合该方法汊点结构和计算特点进行并行计算开发，进一步提升模型的响应速度，同时优化流量系数的确定方式，减少替代误差对计算结果的影响，为开展平原地区智慧水利建设、闸站联合优化调度等复杂调度计算奠定基础。