传染病类突发公共卫生事件风险评估与应对

赵成珍 梁循 王军礼

摘要：突发公共卫生事件会冲击社会经济运行，特别是具备传染性时这种冲击的程度和范围会更深更广，而通过建立模型来模拟传染病类突发公共卫生事件，将为传染病评估和应对提供积极有效的依据。故以SEIR模型为基准，针对SEIR模型存在的不足，将重大传染病事件分为三个阶段发展三阶段模型，将相关参数由静态参数改进为动态参数，分类模拟封城以及传染病存在复发可能性的情形，并利用2020年新冠肺炎疫情数据进行动态模拟。对经典SEIR模型以及改进的三阶段模型分别进行参数估计和系统仿真发现，在无人为干预的自然传播情况下，传染病感染数量峰值会出现在1～2个月后；加强隔离、加大医疗资源投入能显著减小传播规模；改进的三阶段模型能对传染病类事件起到很好的预测作用，可为未来传染病评估和应对提供有效依据。由此，为有效应对传染病类突发公共卫生事件，建议从加强隔离、加大医疗资源投入、疫情后期持续关注等角度着手完善我国传染病应急防控体系，在传染病发生时能够对相关人员做到尽早隔离，提高治愈率，减少传染数量，从源头上降低突发公共卫生事件对经济的负面影响。

关键词：传染病模型；突发公共卫生事件；冲击程度；冲击范围；持续时间

中图分类号：F064.1文献标识码：A文章编号：1007-8266（2020）05-0084-11

收稿日期：2020-04-16

基金项目：教育部人文社会科学项目“供给侧改革、债务率调整与中国宏观经济波动”（19YJC790189）；北京市教育委员会社会科学项目“创新和完善宏观调控体系研究——基于供给侧改革视角”（SM202010037006）；北京物资学院校级项目“新型冠状病毒肺炎传染病模型构建及在城市疫情防控中的应用研究”（2020YQYJ12）

作者简介：赵成珍（1982—），男，山东省滨州市人，北京物资学院经济学院教师，博士，主要研究方向为经济系统的数量建模等；梁循（1965—），男，北京市人，中国人民大学信息学院教授，博士，主要研究方向为社会计算、人工智能、网络金融；王军礼（1978—），男，河南省平舆县人，国务院发展研究中心公共管理与人力资源研究所研究员，北京大学能源经济与可持续发展研究中心研究员，理学博士，主要研究方向为经济系统的量化分析。

一、引言

重大传染病疫情、重大食物和职业中毒等突然发生、可能或已经严重影响公众健康的事件统称突发公共卫生事件。突发公共卫生事件具有严重的社会经济危害性。在目前人口流动速度不断加快、生态环境不断恶化的情况下，突发公共卫生事件时有发生，给相关国家造成了一定的损失。及时有效处理各类突发公共卫生事件，是维护国家和社会稳定、保障人民生命安全的重要手段。

在传染病类突发公共卫生事件中，由于传染病具有很强的传染性，且随着经济和政治的全球化、交通的日益便利，人员流动速度和商品贸易数量不断增加，不仅加大了突发事件在区域之间的关联度，而且加剧了传染病的快速传播。2003年的非典型肺炎（SARS）、2009年的H1N1流感、2014年的埃博拉以及2020年的新型冠状病毒感染肺炎（以下简称“新冠肺炎”）等重大传染病疫情暴发后，经济最先受到冲击的就是旅游业、餐饮业、零售业及交通运输业。比如，根据国家统计局数据，在2003年5月非典型肺炎疫情的高峰期，我国内地入境旅游人数同比下降31%，餐饮营业额同比下降15.5%，铁路客运量同比下降62.5%，社会消费品零售总额增速降至4.3%，此外确诊者及其密切接触人群的治疗和隔离也造成了劳动力规模的下降。重大传染病一旦暴发，会威胁经济贸易的发展和人类的生命安全，其影响的范围和严重性一般远高于其他类型的突发公共卫生事件，因此世界各国一直都在关注传染病的防治问题，我国在应对传染病方面也付出了巨大的努力。中华人民共和国成立之前，鼠疫、天花、霍乱、血吸虫病等反复暴发。中华人民共和国成立之后，不断制定和完善法律法规，坚持扩大对公共卫生事业的投入，取得了显著成就，不仅消灭了霍乱、天花，战胜了非典型肺炎等突发传染病，流行传染病的结构也发生了变化，过去流行的传染病发病率不断下降。

重大传染病疫情发生时，一个国家拥有一套完善的能够有效管理突发公共卫生事件的应急防控体系是非常重要的。而相对于非典型肺炎疫情等其他突发公共卫生事件，新冠肺炎是近年来我国乃至全球感染人数最多、波及范围最广、对经济影响更大的突发重大传染病，在众多突发公共卫生事件中比较具有代表性。而且，对新冠肺炎疫情的应对尽管体现了我国自2003年非典型肺炎疫情之后应急防控体系极大的完善和进步，但同时也暴露了我国应急防控体系中依然存在的问题和不足。因此，本研究利用此次新冠肺炎疫情数据，在传统SEIR模型基础上改进传染病动力学模型，通过模型模拟疫情扩散发展过程和趋势，既可为以后传染病类突发公共卫生事件防控措施的制定和效果评估提供科学依据，也可为目前我国应急防控体系存在的问题提供行之有效的建议，以便快速及时有效地应对突发公共卫生事件，避免问题持续发酵导致更严重的经济损失。

二、文献概述

通过建模求解研究传染病的历史最早可以追溯到1760年，贝努利（Bernoulli D）[ 1 ]通过建立模型研究接种疫苗即牛痘对天花病毒传播的影响。哈默（Hamer W H）[ 2 ]通过建立离散时间模型了解麻疹流行的复发情况，并创造性地假设了发病率，即每单位时间的新增病例数取决于易感者与确诊者数量的乘积。罗斯（Ross R）[ 3 ]通过建立传染病的微分方程模型，研究疟疾在蚊虫和人类间的传播行为，结果发现，若将蚊虫数量控制在临界值以下，疟疾的流行将得到控制，罗斯还凭借对疟疾在蚊子与人类间传播动力学的研究获得1902年第二届诺贝尔医学獎。随后，其他的确定性传染病模型也不断被提出。20世纪初，数理流行病学逐渐兴起，对传染病模型的研究愈发深入。克马克（Kermack W O）等[ 4 ]通过对黑死病等的研究，将被研究地区的人群分为三类，分别是易感者（Suscep？ tible）、确诊者（Infective）、康复者（Recoverer），提出了著名的SIR仓室模型，适用于描述通过病毒进行传播的传染病。随后，克马克等[ 5 ]又在SIR仓室模型基础上创建SIS仓室模型，提出了著名的阈值定理。但是，由于很多传染病在发病前通常会有一定时间的潜伏期，比如艾滋病的潜伏期一般为2年到12年，狂犬病的潜伏期一般为1～3个月，多则可达几十年，因此考虑到潜伏期的因素，后来的研究在SIR模型的基础上不断完善，增加了一个新的传染病群体，即潜伏者（Exposed），提出了SEIR模型。

近年来，国内学者结合我国各时期传染病数据，多次应用SEIR模型，并对之进行改进。徐恭贤等[ 6 ]通过建立SEIR模型对有潜伏期且治愈后终身免疫的非典型肺炎疫情進行研究，实验数据表明，模型模拟结果与疫情实际情况比较吻合。王莲花等[ 7 ]利用总人口具有种族动力学且具有一般传染率的SEIR模型证明，地方病具有全局渐进稳定性。王树忠等[ 8 ]研究了潜伏期和感染期均具有传染性的SEIR模型，并最终得出结论，即对于潜伏期和感染期均具有传染性的传染病，只有控制潜伏者和确诊者人数，才能有效控制疫情传播。吴昊澄等[ 9 ]拟合SEIR模型研究浙江省的学校流行性腮腺炎疫情，对比不同条件下应急接种所达到的效果发现，学校越早实行应急措施，越早应急接种，控制效果越好。崔景安等[ 10 ]根据手足口病具有潜伏期的特征，应用SEIR模型预测北京市手足口病流行趋势，为手足口病预防控制提供参考。李冬梅等[ 11 ]建立的SEIR模型假设潜伏期具有常数输入率，证明疾病模型仅存在地方病平衡点，其基于我国2009年甲型流感病毒实际数据的模拟结果表明，严格控制处于潜伏期的病毒携带者进入可有效控制和消除疫情。黄璜等[ 12 ]分别从自然传播和采取不同隔离防控措施的角度构建诺如病毒SEIR模型，为防止医院暴发性感染诺如病毒提供了理论支持。王昕炜等[ 13 ]基于SEIR仓室模型，在潜伏者向确诊者转化过程中引入时滞参数刻画潜伏期特性，发现在最优疫苗接种策略情况下可有效控制传染病传播。

总体来看，目前尽管SEIR模型已被应用于很多流行传染病的分析，但很少有实证研究探讨影响面如此之广的传染病事件，且现有研究在估计参数时大多用整个过程估计出一个值，不符合现实不同阶段的情况。本研究将重大传染病事件分为三个阶段，并对参数的估计加以改进，把死亡率和康复率作为时变量进行疫情趋势模拟，更符合现实情况，可为实施相关措施以解决影响社会经济发展的源头问题提供思路。

三、研究设定与模型构建及模拟

本研究以SEIR模型为基准，在此基础上进行改进。本研究将传染病流行范围内的人划分为四类：一是易感者（记为St），代表t时刻未感染但有可能被感染的人群；二是潜伏者（记为Et），代表t时刻已经被感染但尚未表现出发病症状且具有传染能力的人群；三是确诊者（记为It），代表t时刻已经感染病毒并表现出相应的发病症状，且具有传染能力的人群；四是康复者（记为Rt），代表t时刻已经康复且不会再被感染的人群，不再影响系统动力学行为。

（一）无人为干预时传染病模型构建与模拟

1.模型假设

借鉴传统经典模型的假定，加之传染性疾病暴发时间较短，且从流行到结束一般不会持续很长时间，因此本研究进行以下假设：

（1）假设总人口为N，保持不变，不考虑人口的迁入和迁出，忽略人口自然出生和死亡对N的影响，即：

2.模型传播机制

无人为干预情况下的模型传播机制参见图1。

为单独观测康复者人数变化，传播机制中的R仅代表康复者。σ代表单位时间内潜伏者转化为确诊者的比例，即潜伏期的倒数。γ代表确诊者的单日康复率，简称康复率或治愈率。v代表确诊者的单日死亡率，简称死亡率。仅进行普通治疗，不防控即自然传播情况下的经典SEIR模型微分动力学方程为：

3.参数设定

本研究分析的传染病流行范围是以湖北省为例，因此经典模型的参数估计基于湖北省疫情数据计算得到死亡率v和康复率γ。图2展示了湖北省2020年1月24日至2020年3月30日的疫情情况。由图2可以看出，2020年2月2日之前，由于样本量较小，数据特征不稳定，如单日死亡率和单日康复率波动较大，但2月2日之后数据特征趋于稳定。因此，选取2020年2月2日作为实证分析的起始点，以在一定程度上减少评估误差。

2020年2月1日到2月2日疫情详细数据参见表1。其中，单日死亡率指单日新增死亡人数与留存确诊人数之比。比如，2020年2月2日单日死亡率的计算过程为：（294-249）/6 738=0.007。单日康复率的计算方法与之类似。

在经典模型中，死亡率v为由实际数据计算得到的平均死亡率0.007，康复率γ为平均康复率0.007。通过在万德（Wind）金融终端检索，得到2018年湖北省户籍人口为6 172.9万人。设N的初始值N0为6 172.9万人，I的初始值I0为2020年2月2日的留存确诊人数8 565人，R的初始值R0为2020年2月2日的康复人数215人。将I视为潜伏期为0天的人群，设潜伏期在0～14天平均分布，则潜伏者E的人数为确诊者人数的14倍，即E的初始值E0估计为11.991万人。易感者S的初始值S0= N0-E0-I0-R0，即6 160.031万人。从理论上讲，一名患者可以传染2～3人，记为Cn，本研究取Cn为2，潜伏期平均为7天，潜伏者的非线性传染系数β2估计为Cn/7，即0.286。由于确诊者会伴有咳嗽及发热等明显症状，且一般会在医院接受治疗，密切接触其他人群的机会远小于潜伏者，假设其接触其他人群的机会为潜伏者的0.02倍，则确诊者非线性传染系数β1的估计值为0.006。自然传播情况下模型主要参数设置参见表2。

4.模拟分析

现实中，在疫情发生初期，由于目前的传染病预防机制存在一定时滞，比如需要对某种病毒是否存在人传人的情况等进行医学上的论证，相关防控措施一般不会在疫情初期就达到极其严格的程度。因此，在发展初期疫情一般遵循自然传播过程，此时人们尚未意识到该病的传染性，不会采取严格的防控措施，医疗资源也不会因此增加。根据假设的自然传播情况下的初始条件以及估计的参数值，本研究利用Matlab软件对经典SEIR模型的微分动力学方程进行数值求解，仿真得到新型冠状病毒自然传播的情况。发展趋势具体参见图3。

从图3的仿真结果可以看出，在自然传播阶段，如果不采取防控措施，且医疗处理水平维持不变，即康复率不变，新冠肺炎的蔓延十分迅速，且感染人群数量庞大，达到千万级别。潛伏者数量在40天左右达到最高峰，之后开始下降；确诊者数量在60天左右达到最高峰，之后开始下降，但要持续很长时间才能下降到较低的水平，一直到300天的时候还有200万左右的确诊者和2万多名潜伏者。可以看出，如果放任传染病发展，将导致劳动力供给大幅下降且持续时间很长，给经济带来长期严重负面影响，因此有必要分析防控措施能否有效阻止疫情蔓延。

（二）积极防控条件下传染病模型构建与模拟

1.模型假设与传播机制

假设对传染病疫情进行积极防控和治疗等，如相关部门在采取一系列措施对易感者、潜伏者、确诊者进行不同程度隔离以降低传染率的同时，积极组织研究新的更有效的治疗方案，加大医疗资源投入，如增加医院数量、增加医护人员数量、增加收治率、提高康复率，则传染病经典SEIR模型的传播机制将变为如图4所示的传播机制。

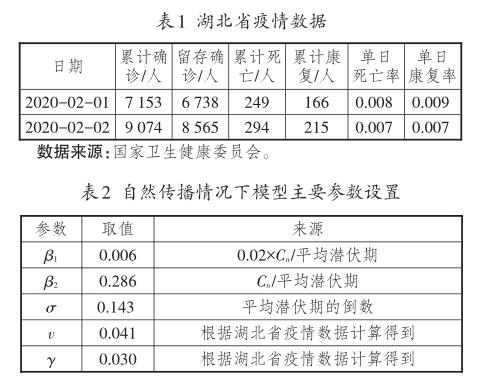
其中，α1代表易感者和潜伏者的暴露程度，由对易感者和潜伏者流动和接触的限制程度决定。α2代表确诊者的暴露程度，由医护治疗期间医院内部对确诊者隔离治疗的程度决定。α1和α2的值越低，代表隔离措施越严格。g代表医疗资源提升程度，收治率越高，医疗方案越有效，g值越大，即治疗康复率越高，死亡率越低。根据积极防控条件下的疫情传播机制，SEIR模型的微分动力学方程可以表示为：

2.模型结果分析

本研究通过调整参数α1、α2、g的大小来模拟对易感者、潜伏者、确诊者不同隔离程度以及不同医疗资源强度下疫情的发展趋势，采用科学方法评估防控措施的效果。当参数α1分别取1、0.5、0.1时，即针对易感者和潜伏者的隔离措施越来越严格时，潜伏者、确诊者数量的发展趋势可分别由图5、图6看出；当参数α2分别取1、0.5、0.1时，即针对确诊者的隔离措施越来越严格时，潜伏者、确诊者数量的发展趋势可分别由图7、图8看出；当参数g分别取1、5、10时，即医疗资源投入越来越大时，如增加医护人员、增加床位、研发出特效药等，潜伏者、确诊者数量的发展趋势可分别由图9、图10看出。

在图5和图6中，α1代表对易感者和潜伏者的隔离程度，1代表不隔离，0.5代表隔离程度中等，0.1代表隔离程度高。由图5可以看出，当α1=1时，代表自然传播情况下潜伏者数量的发展趋势，潜伏者数量先经历40天的上升期，最高峰时超过1 000万人，150天后才下降至16万人；当α1=0.5时，即采取某些隔离措施使有效接触率降低一半时，潜伏者数量自隔离措施实施起开始下降，到51天时便降至1万人；当α1=0.1时，即采取更加严厉的隔离措施时，数量也是自隔离措施实施起开始下降，只需要18天，潜伏者数量便可降至1万人。从三种情况下潜伏者数量发展趋势的仿真结果可以看出，针对易感者和潜伏者的隔离措施越严格，潜伏者数量越能得到有效控制。也就是说，对易感者和潜伏者采取隔离措施可对整个疫情控制起到正向作用。

由图6可以看出，对易感者和潜伏者采取隔离措施，对控制确诊者数量也起到了很好的作用。在自然传播情况下，确诊者数量在66天时达到最高峰，超过3 000万人，且300天后才降至200万人左右；如果采取某些隔离措施使易感者和潜伏者的有效接触率降低一半，即α1=0.5时，确诊者数量在32天时便达到最高峰，仅17万多人，并于300天后降至2.7万人；如果对易感者和潜伏者采取比较严格的隔离措施，即α1=0.1时，则在18天时就达到最高峰，仅10万多人，并于300天后降至2 000多人。从确诊者数量的发展趋势也可以看出，对易感者和潜伏者采取隔离措施可对疫情控制起到比较明显的作用。一方面，可使确诊者数量更早地达到峰值，有效缩短疫情持续时间；另一方面，可有效降低确诊者数量。但同时我们也发现，在仅仅采取隔离措施的情况下，疫情后半阶段仍然会持续较长时间。因此，对易感者和潜伏者采取隔离措施有助于缩小传染病导致的劳动力供给缺口，但经济受疫情影响的持续时间仍然较长。

在图7和图8中，α2代表对确诊者的隔离程度，1代表不隔离，0.5代表隔离程度中等，0.1代表隔离程度强。针对确诊者采取不同程度的隔离措施，可对潜伏者和确诊者数量控制起到一定作用，但效果不是特别明显。这主要是因为，一方面，确诊者数量相对于潜伏者和易感者数量来说还是很少的；另一方面，确诊者一般都在医院接受治疗，这本身就已经自然限制了其接触大量人群的机会。因此，对确诊者继续加强隔离的防控效果不如对易感者和潜伏者继续加强防控的效果明显。但是，考虑到确诊者传染的人群以医护人员为主，而医护人员被传染对医疗资源来说是一种损失，因此加强对确诊者的隔离，从另外一个层面来看，是一种对医疗资源的加强。本研究的实证分析也表明，医疗资源的加强对疫情控制效果明显，因此对确诊者采取隔离措施也比较重要。

在图9和图10中，g代表医疗补给程度，1代表医疗资源不变，5代表医疗资源补给程度中等，10代表医疗资源补给程度高。当加大医疗资源投入时，潜伏者数量的变化趋势主要表现为峰值的降低，尽管起到了一定的作用，但效果不是很明显。确诊者数量的变化趋势一方面表现为峰值的降低，且效果特别明显，说明尽管加大医疗资源投入对潜伏者数量控制效果一般，却可以十分有效地控制确诊者数量暴发的程度；另一方面表现为疫情后半阶段持续时间的大幅缩短，有助于更快地控制疫情。可见，采取积极的医疗措施不仅有助于缩小疫情导致的劳动力供给缺口，而且可以缩短经济受疫情影响的持续时间。

如果综合运用以上疫情防控措施，即在对易感者、潜伏者、确诊者采取严格隔离措施的同时，加大医疗资源投入，令模型参数α1=0.1，α2=0.1，g= 10，则疫情防控效果如图11所示。可以看出，潜伏者数量自开始就一直下降，在18天时便降至1万人以下，确诊者数量在9天时达到最高峰65 000多人，45天可降至1万人。对比图3所示的自然传播情况，理想假设下的积极治疗加隔离防控措施，既可以通过降低感染数量缩小劳动力供给缺口，又可以通过缩短疫情持续时间更早解决冲击经济的源头问题。

（三）三阶段传染病模型构建与模拟

1.三阶段模型的数据基础

模型把人群分为易感者、潜伏者、确诊者、康复者四类，这样在设定初始值时可能会导致易感者数量初始值偏大。从此次湖北省新冠肺炎疫情看，最初暴发区域仅限于武汉，如果直接以湖北省总人口减去其他三类人群数量的差值作为易感者数量，显然不符合现实。SEIR模型的相关应用研究在进行相关参数估计时，一般将疫情的整个过程当成一个阶段来估计，但考虑到现实中疫情会受到媒体报道以及政府紧急防控政策等的冲击和影响，参数估计会随疫情阶段的变化而改变，因此本研究在分析疫情趋势时，尝试对疫情进行分阶段考虑，把人员流动趋于稳定的阶段作为分析的起始点。这样既可以获得更加符合现实情况的参数估计，又由于在疫情扩张期，随着时间的推移，易感者覆盖范围越来越广直至覆盖全省，可以在一定程度上纠正易感者数量初始值偏大的问题。

根据本次疫情发展的时间轴，本研究将之大致划分为三个阶段。第一阶段为自然传播期，从2019年12月8日第一例患者出现开始至2020年1月19日武汉通报一夜新增136名患者为止，在这个阶段公众对本次疫情几乎没有防备，符合自然传播的特征。2020年1月20日，钟南山赴武汉考察，经媒体报道，公众得知新冠肺炎会人传人，加之当时正值春节返乡时段，短时间内武汉有大量人口出城，致使易感区域逐渐扩大到湖北全省。从国家卫生健康委员会统计的密切接触者数据（图12）可以发现，新增密切接触者数量从2020年1月20日开始至1月29日一直上升，之后趋于平缓。据此，本研究将2020年1月20日至1月29日这个时间段定义为疫情发展的第二阶段。在此阶段，人员大量流动，医疗资源紧缺，加之新建医院、新增医护人员都需要一定时间，相应的管理应对措施也不能一步到位，死亡率和康复率并未开始改善。2020年1月23日，武汉封城，全国各地陆续采取严格隔离措施，1月30日以后政府防控措施的作用开始显现，本研究将此时点开始往后的时间段定义为第三阶段。

2020年2月7日晚湖北省新型冠状病毒感染肺炎疫情防控指挥部在例行新闻发布会上汇报的情况显示，武汉市28家定点医疗机构床位增加到8 895张，火神山医院1 000张病床已经交付使用，雷神山医院1 600张病床计划于2月8日交付使用。截至2020年2月6日，国家及各省市共派遣99支医疗队9 277人支援武汉。可以看出，在此阶段，随着医疗资源的不断补充，死亡率和康复率逐步改善（具体参见表3），因此对模型中的死亡率和康复率也要进行相应调整，以使模拟效果更符合现实情况。

2.三阶段模型构建与参数拟合

为验证改进模型在疫情预测模拟方面的有效性，实证分析起始点的选择应尽量靠前，因为越早进行比较准确的预测，越可及时为疫情防控提供合理参考依据。此外，也要考虑疫情数据特征的稳定性。根据前面的分析，在疫情发展的第三阶段选择预测的起始点相对比较合理。还有，我们对疫情阶段的划分是以重大事件的发生为依据的，而从具体事件的发生到疫情数据的体现存在一定的时滞，这个特点从表3的疫情数据也可看出，死亡率和康复率在2020年2月7日以前变化幅度相对较大。综合以上分析，最终选取2020年2月7日作为模型预测模拟的起始点。

第三阶段的传播机制仍然如图4所示，但在此阶段，随着医疗资源的不断补充，死亡率和康复率均呈现出稳定的改善趋势，因此本研究将模型中的康复率γ和死亡率v设为时变量，初始值分别为表3中的0.010和0.004。改進的模型方程为：

假设N的初始值N0为湖北省人口6 172.9万人，I的初始值I0为2020年2月7日留存确诊者数量20 662人，R的初始值R0为2020年2月7日康复者数量832人。由于第三阶段隔离措施已经加强，因此潜伏者E的数量不再等于2020年2月7日确诊者数量的14倍，本研究将此阶段E的初始值E0估计为2020年1月30日留存确诊者数量的14倍，即60 676人。易感者数量S的初始值S0=N0-E0-I0-R0，即61 646 830人。

改进的模型参数仍然取α1=0.1，α2=0.1，除死亡率和康复率外，其他参数仍然参照表2，医疗资源强度系数g=1，表示暂时没有特效药，但医护资源稳步改善，表现为模型中的康复率γ和死亡率v变成了时变量。

3.实证结果与模型有效性评价

按照改进的模型和优化的参数设计，本研究得出的仿真结果如图13所示。现实中此阶段的防控措施比较严格，医疗资源也源源不断地支援湖北，在这样的假设下模拟结果显示，潜伏者数量立即得到控制，一直处于下降状态。得益于严格的隔离措施，潜伏者数量在初期可以保持较快的下降速度，后期随着基数的减少，下降幅度趋于平缓，最终完全得到控制；确诊者数量由潜伏者转化而来，继续经历了一段上升期，但10天后便达到最高峰54 000人左右，之后一直下降，这主要得益于隔离措施的严格（使潜伏者数量不断减少）和医疗资源的加强（使康复率不断提高）；康复者数量增长较快，但随着确诊者数量的不断减少，康复者数量的增长最终也趋于平缓。总体来看，疫情自防控措施实施起就可以快速往好的方向发展，并在50天后慢慢进入尾声。留存确诊者数量预测数据与实际数据对比结果参见图14，说明改进的模型具备预测疫情的可靠性。

4.对封城措施的模拟分析

一个很有效的控制疫情的办法就是尽早隔离。现实结果显示，疫情暴发初期，疫情发源地并未得到较好的隔离处置，待到采取暂停公共交通等封城措施时，已有大量潜伏者和确诊者流出武汉，这在理论上直接增加了易感者的数量。如果在疫情暴发初期就对武汉采取封城措施，疫情控制效果能否更好？本研究利用改进的SEIR模型对此进行模拟仿真。从国家卫生健康委员会官网发布的通知可以看到，截至2020年1月19日22时，武汉市累计报告新冠肺炎病例198例，已康复出院25例，死亡3例。《武汉统计年鉴》公布的2018年末武汉市常住人口为1 108.1万人。假设疫情初期即2020年1月19日之前疫情没有蔓延到武汉市以外，如果当时对武汉采取封城措施，将疫情控制在武汉市内进行处理，则模型中总人口N的初始值N0为武汉市常住人口1 108.1万人，I的初始值I0为170人，R的初始值R0为25人。潜伏者E的初始值E0估计为确诊者的14倍，即2 380人。易感者S的初始值S0= N0-E0-I0-R0，即11 078 425人。假设采取严格的隔离措施，即模型参数仍取α1=0.1，α2=0.1，由于早期的死亡率和康复率尚不稳定，不具有一般规律性，因此本次模拟对死亡率和康复率的估计仍然采用前文对第三阶段的时变设计。其他参数仍然参照表2，医疗资源强度系数g=1，表示暂时没有特效药，但医护资源情况稳步改善。模拟得出的疫情发展情况参见图15。

可以发现，隔离以及医疗资源等防控措施影响着疫情的走势，但前期对疫情暴发地采取的封城措施决定了易感者的基数。在模拟封城10～11天后，确诊者数量达到峰值1 600多人，50天后，确诊者数量僅剩48人，可以说疫情完全得到了控制。但是，如果没有及时封城，导致整个湖北省都成为易感区，疫情完全得到控制要经历更长的时间，且影响范围更广。因此，及时采取封城措施一方面可以缩小疫情对经济的影响范围，另一方面可以更快地解决源头问题，推动经济更早地进入恢复期。

5.对传染病存在复发情况的模拟分析

尽管我国在2003年应对非典型肺炎疫情时已经积累了一些经验，如要对患者进行隔离，但在应对本次传染病疫情时，却因多了潜伏者具备传染性这个特征而没有及时重视对潜伏者的隔离。因此，在面对类似重大传染病疫情时，需要在总结以往防控经验的基础上，多考虑一些有可能出现的传染病特征。比如，近期有证据表明，部分患者在康复后仍有可能核酸检测呈阳性，因此我们有必要考虑传染病复发的可能，并通过实证分析得出传染病存在复发可能性时的疫情趋势。

我们在新冠肺炎传染病模型的基础上添加这一假设，即康复者存在一定比例的复发可能性，并再次具有传染性，再次成为潜伏者。假设这一比例为k，可以得出如图16所示的存在复发可能性时的传播机制。

考虑到疫情逐渐得到控制，医护资源不断改善，我们假设k随时间递减，设k的初始值为0.01，即初始时每天有1%的康复者会复发变为潜伏者，但这个比例随着时间的推移到100天时线性递减为0。在图11所示的积极治疗防控情况下，对存在复发和不存在复发两种情况进行仿真对比，结果参见图17。

可以看出，如果存在一定比例的康复者复发，即使比例不大，也会延长疫情持续的时间，进而阻碍社会经济的尽快恢复。因此，传染病疫情防控工作不能忽视对康复者的后续关注。一方面，康复者短期内要继续做好自我隔离，尽量减少可能的传染；另一方面，医疗团队要对传染病是否存在复发可能性进行必要的研究。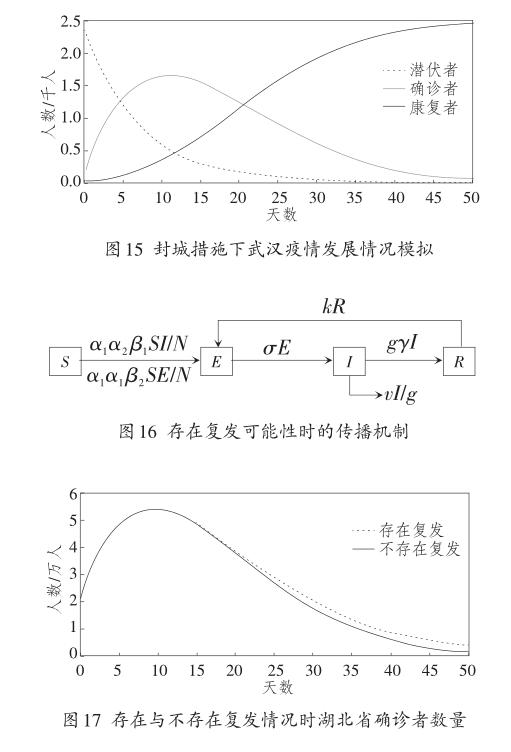

四、结论与建议

（一）结论

本研究以SEIR模型为基准，对处于传染病流行范围的人进行划分，分为易感者、潜伏者、确诊者、康复者四类；对传统经典SEIR模型存在的不足（即估计参数时多以整个过程估计出一个值，不符合现实中不同阶段的情况）进行改进，将重大传染病事件分为三个阶段，发展三阶段模型；对相关参数加以改进，把死亡率和康复率作为时变量，更符合现实情况。通过对经典SEIR模型及改进的三阶段模型分别进行参数估计和系统仿真，可得出以下三个主要结论：

1.基于对经典SEIR模型的应用，在无人为干预的自然传播情况下，传染病感染数量峰值会出现在1～2个月后

基于湖北疫情数据进行参数拟合与动态仿真，结果发现，在无人为干预的自然传播情况下，潜伏者数量在40天左右时达到峰值，确诊者数量在60天左右时达到峰值，且要持续很长时间才能降到较低水平。

2.加强隔离、加大医疗资源投入能显著减小传播规模

基于经典SEIR模型，通过调整隔离程度和医疗资源强度参数，模拟不同隔离程度与医疗资源投入下疫情的发展趋势。结果发现，随着对易感者和潜伏者隔离程度的提高，传染病整体的传播规模显著减小；随着医疗资源投入的加大，如增加医护人员、增加床位、研发出特效药等，传染病的传播规模显著减小。通过对湖北疫情进行系统拟合发现，隔离措施严格时，潜伏者数量自隔离措施实施起开始下降，到51天时便降至1万人；隔离措施更严格时，只要18天，潜伏者数量便可降至1万人。同样，加大医疗资源投入后，确诊者数量在9天时达到峰值65 000多人，45天时可降至1万人。

3.改进的三阶段模型能对传染病类事件起到很好的预测作用，可为未来传染病评估和应对提供有效依据

改进的三阶段模型将死亡率和康复率由静态参数变为动态参数进行动态仿真，使得运用改进后的模型预测结果与实际情况拟合度较高，结果误差很小，说明模型预测精度较高，具有可靠性。模型动态仿真结果表明，加强隔离、加大医疗资源投入可使疫情快速往好的方向发展，并于50天后慢慢进入尾声。模拟封城情形发现，模拟封城10～ 11天后确诊者数量达到峰值，50天后确诊者基本消失，说明尽早封城可有效控制疫情规模，进而缩小经济受冲击范围。模拟传染病存在复发可能性的情形发现，若存在一定比例的康复者复发，即使比例不大，也会延长疫情持续时间。

（二）建议

结合本研究模型分析结果，应从严格隔离、加强医疗资源投入、疫情后期持续关注三个角度，对新冠肺炎疫情中依然存在的问题提出合理建议，完善我国传染病应急防控体系，这有助于今后及时有效解决类似突发公共卫生事件，从源头上减少疫情对经济的负面影响。

1.对传染病类突发公共卫生事件尽早隔离

由模型分析可以看出，阻断传播途径是降低感染数量的重要手段。要对突发公共卫生事件做到早发现早处理，就要对传染病信息保持足够警惕和实时关注，如果不能第一时间采取有效措施消除隐患，传染病一旦暴发，波及范围和损失就会不断扩大。建议完善传染病直报系统，扩展传染病直报系统职责范围，方便新发传染病信息及时上报，帮助政府决策。

重大突发传染病疫情中全国各地医护人员普遍缺乏医疗物资的现象反映了我国医用应急物资储备不足的现状，国家应设立专门机构在国内建立应急医疗物资储备体系，动态管理，定期更换补充应急物资，灵活管理应急物品储备，在储备物品临近保质期或保质期限超过一半时派发到一线医院使用，避免浪费。疫情一旦发生，由主管的地方政府和部门及时将应急物资送往医院等抗疫一线机构，协助做好医护人员和患者的隔离，避免医护人员交叉感染。

2.增加投入提高康復率是降低传染数量的重要手段

由模型分析结果可以看出，提高康复率是降低感染数量的又一重要手段，因此需要加强对医疗资源的集中整合。目前，我国一线二线城市与大部分中小城市、农村及偏远地区的公共卫生服务水平差距较大，政府对农村及偏远地区公共卫生管理的财政投入仍然较少，公共卫生人才主要集中于大中城市，面对类似此次新冠肺炎的传染病等突发公共卫生事件，农村及偏远地区的医疗服务水平明显不足，基层疾病防控机构卫生应急专业能力相对不足，高素质复合型人才短缺，处理重大传染病疫情的专业队伍缺乏，难以有效应对。因此，需要加大对农村及偏远地区医疗方面的财政投入，提高农村及偏远地区应对传染病等突发公共卫生事件的能力，满足其开展公共卫生管理的基本需求。

*感谢北京物资学院硕士研究生赵辉、赵淑梦对本研究的贡献。

参考文献：

[1]BERNOULLI D.Essai dune nouvelle analyse de la mor？ talitécausée par la petite vérole et des avantages de linocu？ lation pour la prévenir[D].Paris：AcadéMie Royale Des Sci？ ences，1976.

[2]HAMER W H.The milroy lectures on epidemic diseases in England——the evidence of variability and of persistency of type[J].The lancet，1906，167（4 305）：569-574.

[3]ROSS R.The mathematics of malaria[EB/OL].[2020-04-05]. https：//www.bmj.com/content/1/2626/1023.1.

[4]KERMACK W O，MCKENDRICK A G.A contribution to the mathematical theory of epidemics[J].Proceedings of the royal society of london，1927，115（772）：700-721.

[5]KERMACK W O，MCKENDRICK A G.Contributions to the mathematical theory of epidemics-II. the problem of ende？ micity[J].Bulletin of mathematical biology，1991，53（1-2）：57-87.

[6]徐恭贤，冯恩民，王宗涛，等.SARS流行病的SEIR动力学模型及其参数辨识[J].黑龙江大学自然科学学报，2005（4）：459-462.

[7]王莲花，刚毅，张凤琴.具有常数输入的SEIR模型的稳定性分析[J].数学的实践与认识，2009，39（18）：208-214.

[8]王树忠，刘晓宇，李冬梅.一类潜伏期和染病期均有传染力的SEIR模型的稳定性分析[J].哈尔滨理工大学学报，2010，15（2）：71-75.

[9]吴昊澄，王臻，何凡，等.基于SEIR模型的流行性腮腺炎暴发疫情控制效果评价[J].中国预防医学杂志，2013，14（1）：72-75.

[10]崔景安，叶萌，宋国华，等.北京市手足口病的流行趋势预测[J].生物数学学报，2014，29（1）：131-135.

[11]李冬梅，桂春羽，温盼盼.一类潜伏期具有常数输入率的SEIR模型在流感防控中的应用[J].数学的实践与认识，2015，45（12）：160-166.

[12]黄璜，兰玲，单旭征，等.SEIR模型在诺如病毒医院感染的应用研究[J].中华医院感染学杂志，2018，28（14）：2 205-2 208.

[13]王昕煒，彭海军，钟万勰.具有潜伏期时滞的时变SEIR模型的最优疫苗接种策略[J].应用数学和力学，2019，40（7）：701-712.

Risk Assessment and Response of Public Health Emergencies in Infectious Diseases

ZHAO Cheng-zhen1，LIANG Xun2and WANG Jun-li1

（1.School of Economics，Beijing Wuzi University，Beijing 101149，China；2.School of Information，Renmin University of China，Beijing 100872，China；3.Institute of Public Management and Human Resources，Development Research Center of the State Council，Beijing 100010，China）

Abstract：Major public health events will impact the socio-economic operation，especially when it is contagious，the extent and scope of such impact will be more serious. Establishing the model can help us to simulate public health emergencies in infectious diseases；and it will provide us with the effective basis for the evaluation and countermeasures of that. Based on the SEIR model and considering its deficiency，the authors develop a three-step development model，change related parameters from static ones to dynamic ones，simulate the situation of lockdown and reappearance possibility，and carry out the dynamic simulation based on data of new coronavirus outbreak in 2020. It is found that：under the situation of no human intervention，the peak number of infections will appear in one or two months；strengthening isolation and increasing medical investment will significantly reduce the scale and scope of outbreak；and the improved three-step model can play its role in forecasting infection related issues，and it can provide us with effective basis for the evaluation and countermeasures of the infection in the future. Therefore，to effectively cope with the public health emergencies，we should，first，perfect out prevention system from aspects such as restricting isolation，increasing investment in medical resources and continuously focusing on this issues；second，we should isolating related person as early as possible with the happening of diseases and improve the recovery rate to reduce the number of infections，and reduce to fundamentally weaken the negative impact on economy.

Key words：infectiousdiseasemodel；publichealthemergency；levelofimpact；extendofimpact；thedurationoftheoutbreak