大跨连续梁拱组合桥梁拱分担比例实验探究

夏文传 任利锋² 周智宏²

（1.兰州交通大学，甘肃 兰州 730070；2.华邦建投集团股份有限公司，甘肃 兰州 730070）

一、实验概况

（一）实验模型

某黄河大桥跨径为80m+150m+80m，矢跨比1/5，主梁采用单箱三室。有机玻璃模型以该桥为背景，模型全长440.8cm，主梁跨径为214.3cm，边跨跨径采用113.6cm，截面形式采用单箱三室直腹板截面，如图1所示；模型中采用21组吊杆，吊杆采用钢丝，顺桥向间距85.7mm，桥面横桥向间距287mm，如图2所示。为研究矢跨比、梁拱刚度比，共制作7个有机玻璃模型，如表1所示。分别对每一模型采用1kg、3kg和5kg的力进行索力张拉，共组合成21个模型。

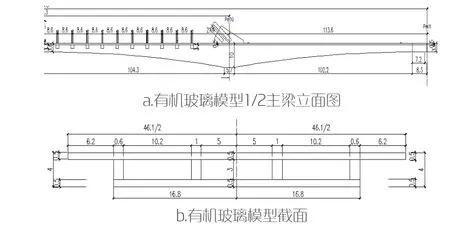
图1 有机玻璃模型(单位：cm)

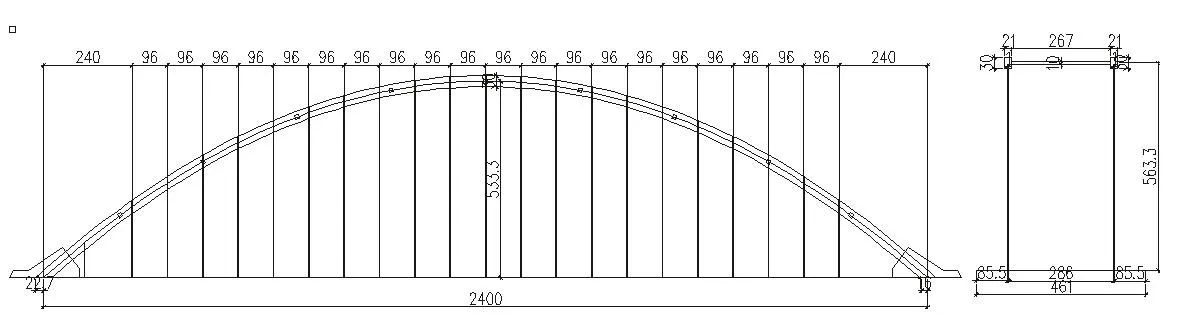
图2 矢跨比1/4.5，刚度比41.2的有机玻璃拱肋截面(单位：cm)

（二）测点布置

实验过程中位移测量截面有边跨支座、两个中跨支座、边跨跨中、中跨1/4、中跨跨中、1/4拱肋和1/2拱肋共8个截面，每个截面2个测点共16个点的位移；应力测量截面有边跨跨中、中跨跨中、中跨1/4截面3种，每个截面30个共90个应力测点。

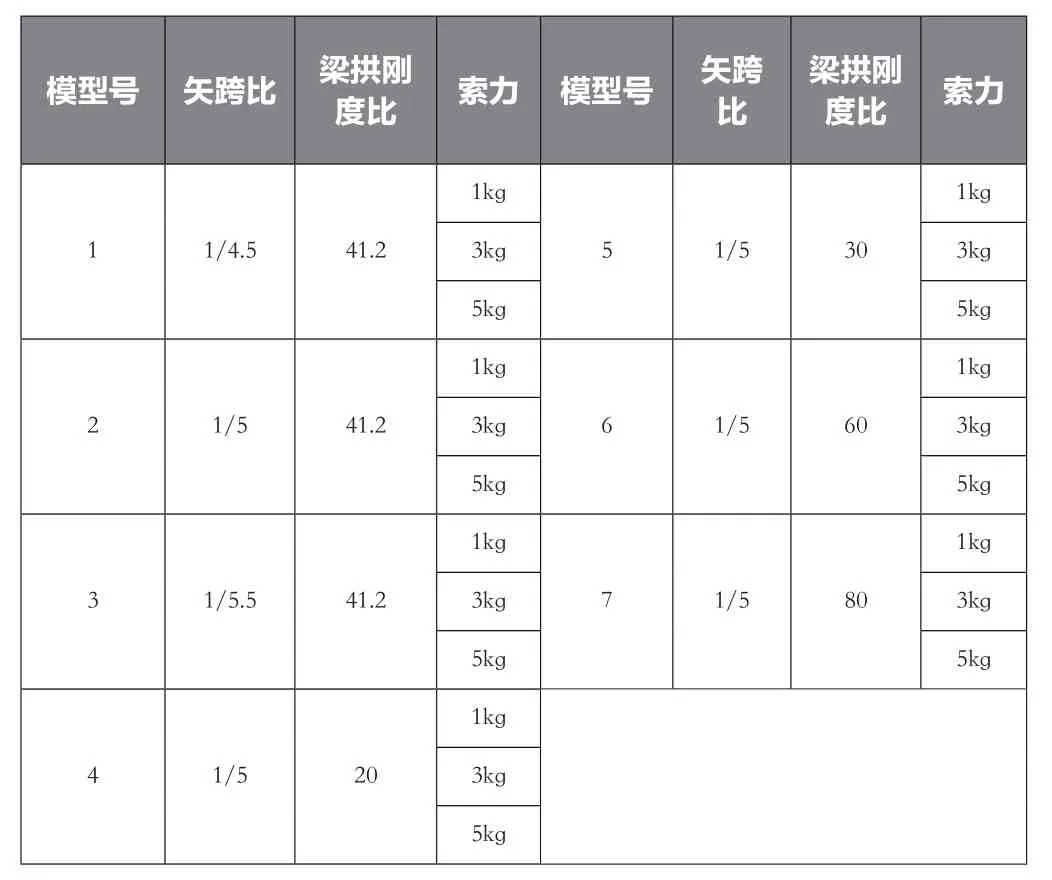
表1 模型参数

（三）实验工况

实验工况包括：边跨跨中截面对称加载、边跨跨中截面偏心加载、中跨1/4截面对称加载、中跨1/4截面偏心加载、中跨跨中截面对称加载、中跨跨中截面偏心加载。加载荷载大小为40.7kg，实验图片如图3所示。

图3 实验加载

模型2(张拉索力5kg时)跨中对称加载时，实测、有限元及简化公式计算结果，如表2所示。

表2 实测、有限元及简化公式计算结果对比表

由表2可知，实测和有限元结果比较接近，简化公式与实测和有限元结果误差较大，误差为4.2%。简化公式计算采用变截面连续梁跨中截面的刚度，刚度比实际模型和有限元模型小，因此梁分担比例小而拱分担比例增大。

二、梁、拱分担荷载比影响因素分析

（一）张拉索力T影响分析

简化公式中rb与T无关，实测和有限元索力对rb也很小，如图4所示。

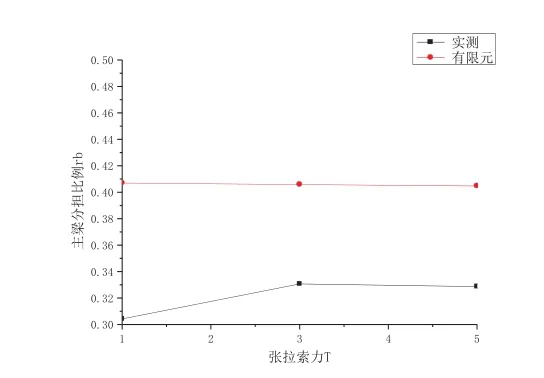
图4 T与 Kha关系

（二）梁、拱抗弯刚度比Kba影响分析

以rb为因变量，Kba为变量，其余为参数，则公式可简化为：

简化公式计算的rb与Kba关系曲线如图5所示，实验和有限元得到的rb与Kba关系如图6所示。从图5、图6可以看出，当Kba≤1时，此时拱肋承担绝大部分荷载，拱肋荷载分担比较大，而主梁分担荷载较少，主梁分担比较小。当48＞Kba＞1时，rb随Kba增大而急剧增大。当56＞Kba＞48之间时，梁拱基本平均分担荷载。当Kba＞56时，此时主梁刚度较大、拱较柔，主梁承担荷载较多，主梁荷载分担比超过拱肋荷载分担比。

图5 ra、rb与 kba关系

图6 rb与 kba关系

（三）吊杆、拱肋等代刚度比Ksa影响分析

以rb为因变量，Ksa为变量，其余为参数，则公式可简写为：

则rb与Ksa关系曲线，如图7所示。从图7可以看出，rb随Ksa增大而减小；当Ksa＜1600时，rb随Ksa变化急剧；当Ksa＞1600时，rb随Ksa变化较缓。

图7 rb与 ksa关系

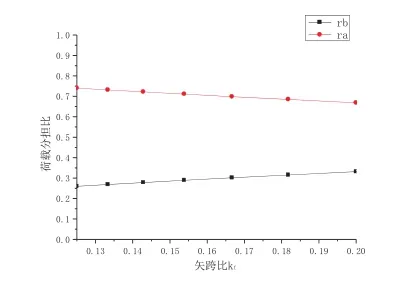
图8 ra、rb与 kf关系

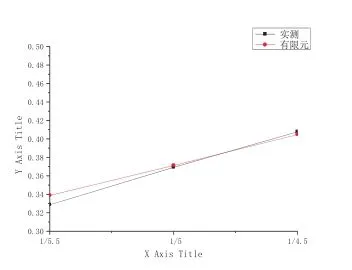
图9 rb与 kf关系

（四）矢跨比Kf影响

以rb为因变量，Kf为变量，其余为参数，则公式可简写为：

简化公式ra、rb与Kf关系曲线，如图8所示，实测和有限元得到的rb与Kf关系曲线如图9所示。从图11、图12可以看出，rb随Kf增大而增大；Kf对rb影响不大。

（五）轴向变形系数Ka影响

以rb为因变量，Ka为变量，其余为参数，则公式可简写为：

则rb与Ka关系曲线如图10所示。从图13可以看出，rb随Ka增大而增大。

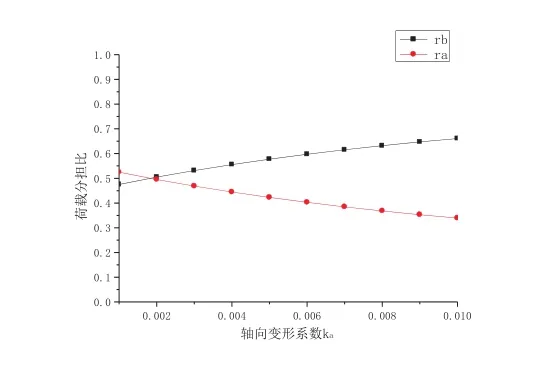
图10 rb与 ka关系

（六）边、中跨跨径比 影响

以rb为因变量，η为变量，其余为参数，则公式可简写为：

则rb与η关系曲线如图11所示。从图11可以看出，rb随η增大而增大，但变化不大。

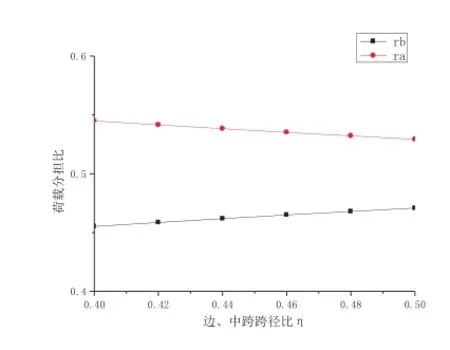
图11 rb与η关系

三、结语

通过对梁、拱肋荷载分担比各影响因素的探究可知：

1.采用基于挠度的梁、拱荷载分担比，能够较好地反映梁拱组合桥梁拱协作机理；同时基于挠度的梁、拱分担比能够利用实桥易于测得的挠度，便于应用于实际工程。

2.当Kba≤1时，此时拱肋承担绝大部分荷载，拱肋荷载分担比较大，而主梁分担荷载较少，主梁分担比较小。当48＞Kba＞1 时，rb随Kba增大而急剧增大。当56＞Kba＞48之间时，梁拱基本平均分担荷载。当Kba＞56时，此时主梁刚度较大拱较柔，主梁承担荷载较多，主梁荷载分担比超过拱肋荷载分担比。由于条件限制，有机玻璃实验只做了梁拱刚度比20、30、41.2、60、80，对于其他比例的缺乏实验数据。

3. rb随Kf增大而增大，ra随Kf增大而减小；Kf对rb影响不大。

4. rb随Ksa增大而减小；当Ksa＜1600时，rb随Ksa变化急剧；当Kba＞1600时，rb随Ksa变化较缓。

5. rb随Ka增大而增大，ra随Ka增大而减小。

6. rb随 增大而减小，但变化不大。

7.张拉索力对rb影响无关。