基于极限学习机的炭化可燃物着火时间预测

翟春婕，王新猛，张思玉

(1.南京森林警察学院信息技术学院，南京，210023; 2.中国科学技术大学火灾科学国家重点实验室，合肥，230026；3.南京工业大学安全科学与工程学院，南京，210009；4.国家林草局森林防火工程技术研究中心，南京，210023)

0 引言

炭化可燃物在火灾早期外界热辐射作用下一般经历升温、水蒸发、热解等复杂物理化学过程并产生热解挥发性气体，当气体浓度及可燃物表面温度达到一定阈值时产生火焰，发生火灾蔓延。深入理解火灾早期炭化可燃物的热解及着火特性从而预测着火时间对于研究火灾蔓延现象、建立火蔓延数值模型具有重要的作用。目前已有很多学者从实验及理论角度开展了研究工作。

Billaud等[1]实验模拟火蔓延锋面辐射热流下固体可燃物的着火时间。Belcher等[2]通过热脉冲形式模拟了火山作用下外部可燃物接收到的辐射热流，发现可燃物含水率越低，植被可燃物越易着火。Didomizio等[3]数值模拟了四阶变化热流下木材温度分布及着火时间，并进行了实验验证。Vermesi等[4,5]利用锥形量热仪设计了抛物线形式的变化热流，实验测定了木材与聚合物的表面温度变化及失重速率，进一步探讨了着火判据的参数选择。Yang等[6]实验研究了线性上升热流下木材热解着火过程，发现着火时刻质量损失速率几乎不变。Reszka等[7]和Lamorlette[8]分别研究了线性上升和多项式热流下固体可燃物着火特性，获得了可燃物着火时间和热流参数的关系。但炭化可燃物的着火时间受到多种因素影响，传统基于解析法预测着火时间时难以考虑，误差较大，基于数值模型进行求解虽然可考虑各因素影响，求解准确，但效率较差。因此需要一种快速准确预测着火时间的方法。

机器学习技术近年来在图像处理、电子商务等领域取得了广泛的应用，并向火灾科学领域渗透[9-11]。随着机器学习技术的诞生，目前已发展了多种训练模型，比如卷积神经网络、BP神经网络等，但这些技术一般训练时间较长，且需要较高的计算机硬件配置。极限学习机(ELM)由黄广斌教授提出[12-15]，与传统神经网络训练相比，ELM通过提高隐藏层神经元数目并随机初始化权值的方式避免了误差反向传播的过程，显著提高了训练效率。由于其具有强大的描述多种因素复杂非线性关系的能力，能够满足炭化可燃物着火时间预测的要求，因此本文提出基于ELM实现着火时间的预测，具有相比解析法更加准确、相比数值法效率更高的优点，在火蔓延模型中具有广阔的应用前景。

1 数值模型

ELM通过一定算法自动训练以寻找数据之间的联系，因此需提供海量数据。虽然目前文献中已有众多测量不同种类炭化可燃物着火时间的实验工作，但一方面数据较少，另一方面由于可燃物物性参数无法连续变化，因此很难提供ELM足够的训练实验数据。炭化可燃物热解模型是火灾科学领域长久以来的热点问题，通过使用数值偏微分方程的方式描述热传导、水蒸发、热解、气体流动等复杂物理化学过程并基于数值方法进行求解，获得热解过程中的各项参数。作者建立了可燃物热解的一维数值模型[16,17]，并与实验结果进行了对比验证，表明建立的数值模型可以准确预测热解参数，因此本文以此一维模型为基础提供海量数据用于训练及验证，模拟结构原理图如图1所示，可燃物在z=0处与外部存在能量及质量交换，z=L处为绝热条件。

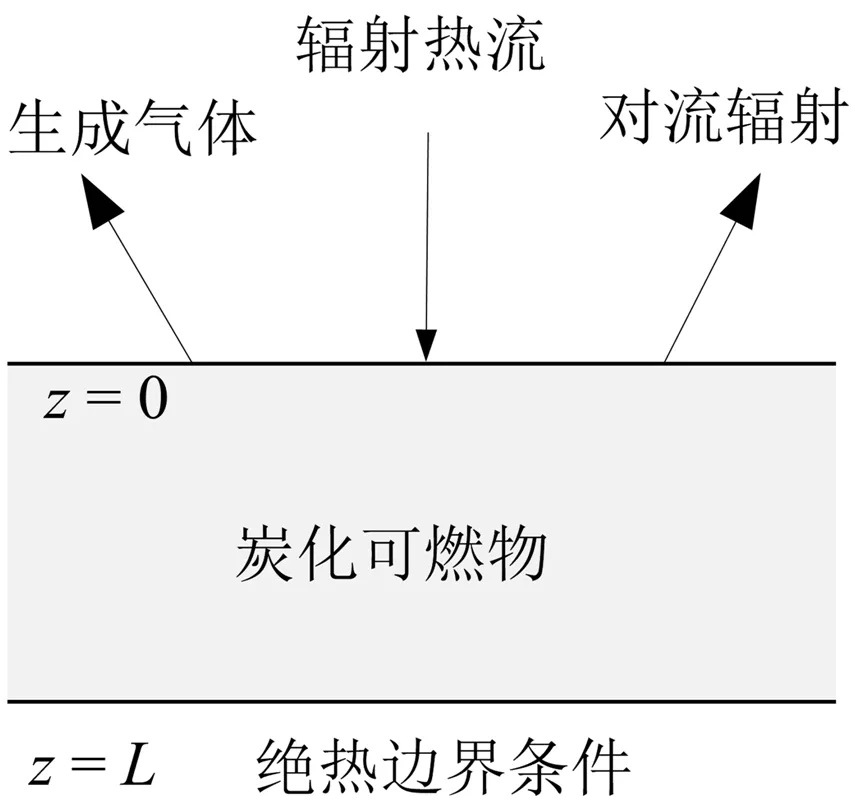
图1 数值模型求解示意图Fig. 1 Schematic of numerical model of combustible pyrolysis

由于模拟中不存在外部着火源，可燃物主要受到外部辐射热流影响升温并自发着火，因此外部辐射热流是影响着火时间的关键因素。但目前一般研究中均将外部辐射简化为恒定热流，经过一系列简化后解析求解可得一维热厚性可燃物的着火时间满足：

(1)

式中tig为着火时间，λ为入射热流。但在推导过程中并未考虑热解反应、水蒸发、对流换热等物理化学过程，导致预测精度偏低。另一方面，已有研究工作表明，火灾早期静态可燃物接收的热流与火焰锋面之间距离有关，因此一般随时间变化，通常可使用多项式形式进行描述。

(2)

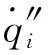
文献[16]中作者经过推导，表明当多项式时变热流作用时着火时间满足：

(3)

可见与恒定热流相比，时变热流作用下着火时间发生了显著变化，预测着火时间时需确定具体热流形式。由于时变热流作用下可燃物接收热流在着火前时刻一般数值较大，而研究表明强热流作用时着火时间的解析公式会出现一定偏差，因此很难通过解析法准确预测着火时间。

数值模型的具体控制方程形式见文献[16]，综合考虑了可燃物升温过程中经历的一系列物理化学过程，通过改变参数进行数值求解可得可燃物不同时刻的温度分布及失重速率等参数。模拟中需要人工提供临界着火判据作为终止模拟的条件，辅助获得着火时间信息。实验表明，恒定热流及时变热流作用时，临界质量损失速率可作为可靠的着火判据，因此本文选择临界质量损失速率作为着火判据。需注意，由于时变热流一般升温过程较短，可燃物中水分并未全部蒸发，因此在发生着火时，水分蒸发同样会导致质量损失，在计算时需排除水分影响，只考虑生成热解挥发分导致的质量损失速率，以此为基础确定着火时间。

2 极限学习机

2.1 ELM基础理论

ELM与经典反向传播(BP)神经网络类似，均属于多层感知器神经网络，结构如图2所示，包含输入层、隐藏层及输出层三个部分，其中输入层连接物性参数及环境参数，输出层连接着火时间。BP神经网络虽然基础理论简单，但训练时神经元之间连接权值需根据输出误差信息进行调节，计算量大、收敛速度低，且易陷入局部最优，无法获得全局最优参数。相比之下，极限学习机神经网络通过证明相关理论简化了BP神经网络训练过程，在满足激励函数在任意区间内无限可微的条件时，可以以连续概率分布随机生成输入层与隐藏层连接权值w和阈值b，并存在一组隐藏层与输出层之间权值使得网络输出满足期望输出。因此在训练中只需选择无限可微激励函数，随机确定输入层与隐藏层之间权值和阈值，即可以获得隐藏层与输出层连接权值的确定解，无需优化迭代过程，能够显著提高训练效率。但ELM为单隐藏层结构，因此当使用ELM时，图2中应只有一个隐藏层。

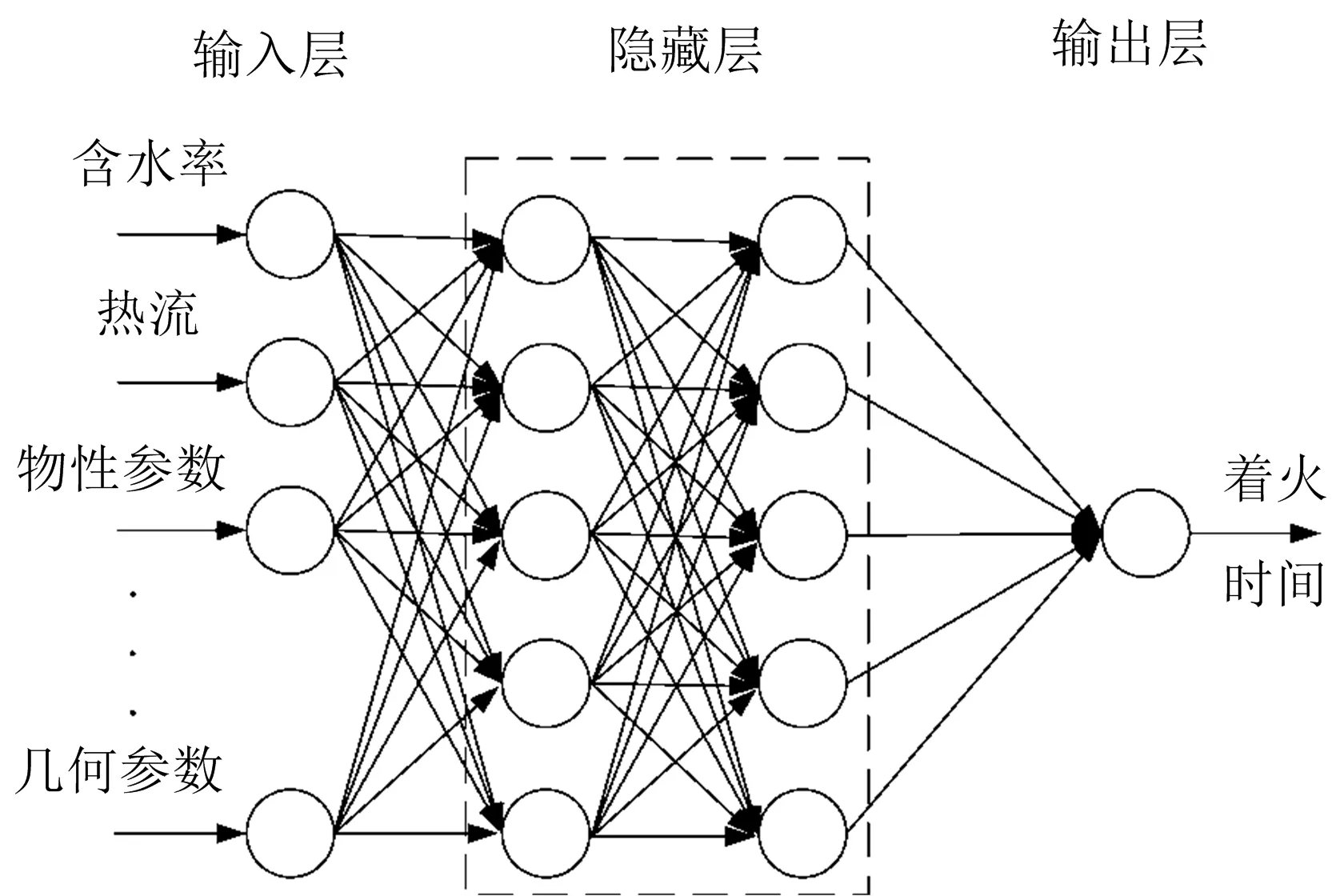
图2 多层感知器神经网络结构图Fig. 2 Multi-layer perception neural network

ELM的详细训练过程如下：

(1)随机赋值输入层与隐藏层之间权值wji及隐藏层神经元阈值bj，隐藏层神经元输出：

(4)

式中f(⋅)为神经元激励函数，满足在任意区域无限可微的条件。

(2)隐藏层输出需与期望输出一致，满足：

Hv=E

(5)

式中v为待求隐藏层与输出层连接权值，E为期望输出，H为隐藏层输出矩阵：

(6)

根据ELM理论基础对任意随机权值wji及阈值bj存在隐藏层权值v，使得网络输出与期望输出一致，可得：

v=H*E

(7)

式中H*为H的广义逆矩阵。由于ELM可通过求解式(7)直接获得权值参数，无需迭代优化，效率较高，且克服了BP神经网络训练中需要根据经验设置训练次数、训练误差等参数的问题。由于基于迭代法求解广义逆矩阵效率太低，本文选择正交投影法进行求解。当隐藏层神经元数小于训练样本数时，权值为：

(8)

反之，权值为：

(9)

式(8)及式(9)两式中，τ为正则参数，可改善模型求解稳定性并提高ELM泛化能力。

2.2 ELM参数组成

炭化可燃物着火时间受到多个参数影响，根据数值模型[16]使用的主要物性及热流参数，本文主要关注热流系数λ、比热容Cw、热导率kw、木材密度ρw(干木材，排除含水率影响)、含水率wmois、对流系数hconv等六个参数。这些参数的数值范围相差较大，为了保证每个参数对网络训练的影响相近，本文对输入参数进行了预处理，输入层部分进行归一化，将参数变化范围线性缩放至[-1, 1]之间，

(10)

式中p为待处理参数，np为归一化参数，mp为参数均值，mp0为参数最大值，mp1为参数最小值。其中β=0时，λ∈[10, 70] kW·m-2，β=1时，λ∈[0.03, 0.6] kW·m-2· s-1，β=2时，λ∈[3e-4, 6e-3] kW·m-2·s-2。Cw∈[1200, 3000] J·kg-1·K-1，kw∈[0.12, 0.3]W·m-1·K-1，ρw∈[200, 900] kg·m-3，wmois∈[0, 1]，hconv∈[6, 16]W·m-2·K-1。

ELM的输出层参数着火时间，变化范围为[10 s, 1 500 s]，若直接将着火时间作为输出参数，求解式(7)时可能对着火时间较长时的参数影响较大，影响高恒定热流及快速上升热流的预测精度，因此本文将着火时间进行对数计算后连接至输出层，计算可知对数后，优化求解式(7)可最小化着火时间的相对误差。

3 结果讨论与分析

本文使用ELM开展了着火时间的预测工作。首先，基于Fortran语言编写了炭化可燃物一维热解数值模型，选择向前差分形式进行求解，随机产生数值在[-1, 1]之间的六维向量并按照式(10)的逆运算获得实际物性及环境参数代入模型，当热解挥发分气体生成速率达到临界质量损失速率时停止计算，保存随机参数及着火时间。分别针对β= 0, 1及2三种情况进行计算，每种情况计算10100组数据，其中10000组数据用于训练，100组数据用于测试验证。

然后基于Matlab语言编写了ELM训练及测试程序，其中输入层神经元数目6个，隐藏层数目2000个，输出层数目1个，激活函数为sigmoid 函数，将上一步骤中保存的随机参数及着火时间分别作为输入层参数及输出层参数代入ELM，开展训练。使用CPU为Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz，训练时间为0.98 s。训练中广义逆矩阵条件数较高，因此正则项τ不可省略，否则可能引入误差。由于隐藏层数目较多，ELM提供了较高的拟合能力，需尽可能增加输入数据覆盖范围避免陷入局部最优以改善泛化能力。

最后以100组随机参数输入ELM，获得着火时间的预测值。表1为不同参数输入时ELM预测着火时间与数值模型求解着火时间的对比，可见在不同参数范围内，ELM均准确预测了着火时间的变化，由于训练中我们已预先对着火时间进行了对数化处理，因此对长着火时间及短着火时间的预测精度相近，综合β= 0，1及2三种情况的平均误差小于3%，而在实验测量着火时间时受到样件不一致性影响不确定度一般达4%，ELM可以实现预测目标。由于给定物性参数后可直接代入ELM获得着火时间，具有很高的效率，因此可在火蔓延模型中代替热解建模部分，提供着火时间的准确信息，提高火蔓延模型的求解速率。

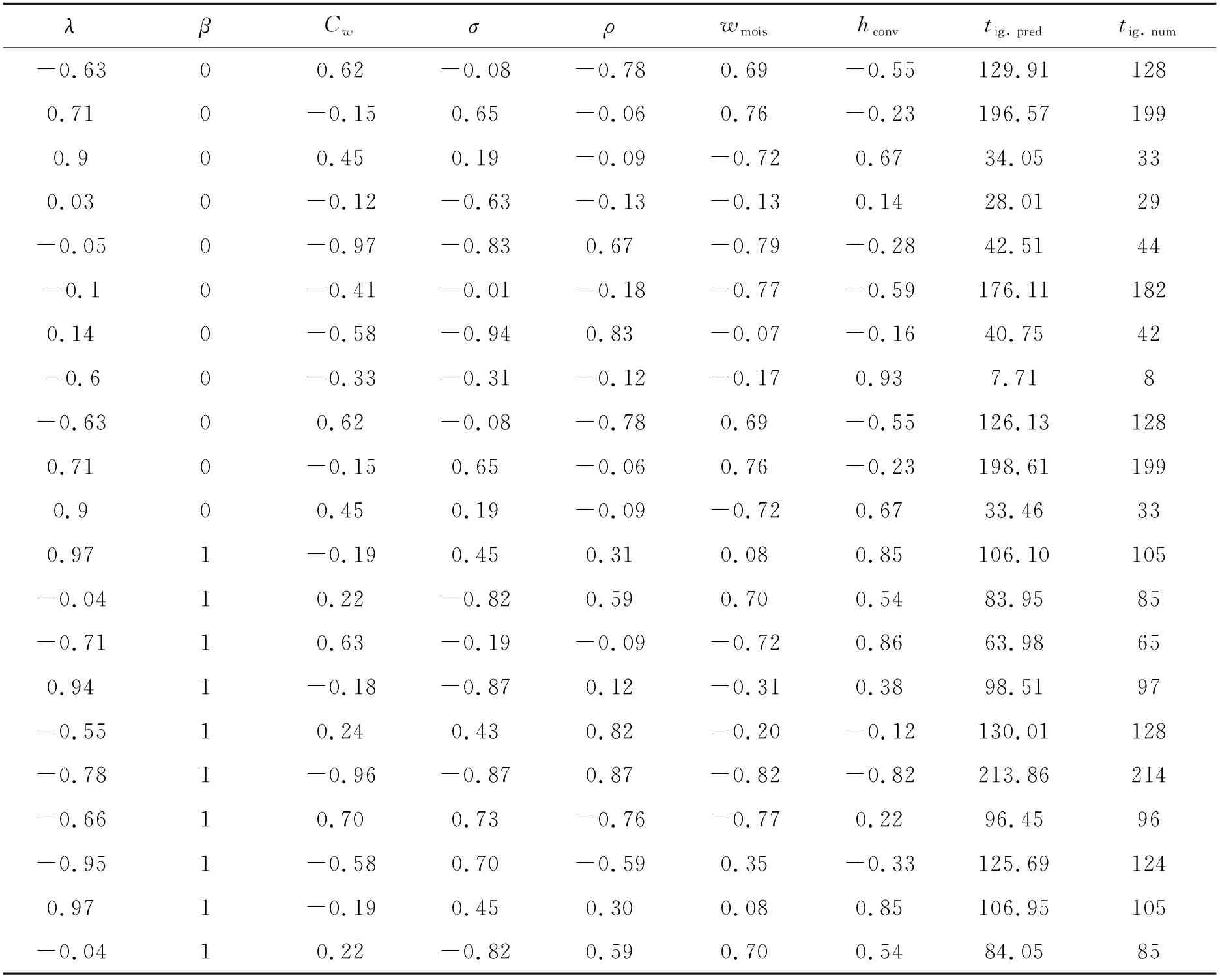
表1 随机参数输入时炭化可燃物着火时间数值与预测值对比tig, pred (s): ELM预测结果，tig, num (s): 数值模型求解结果

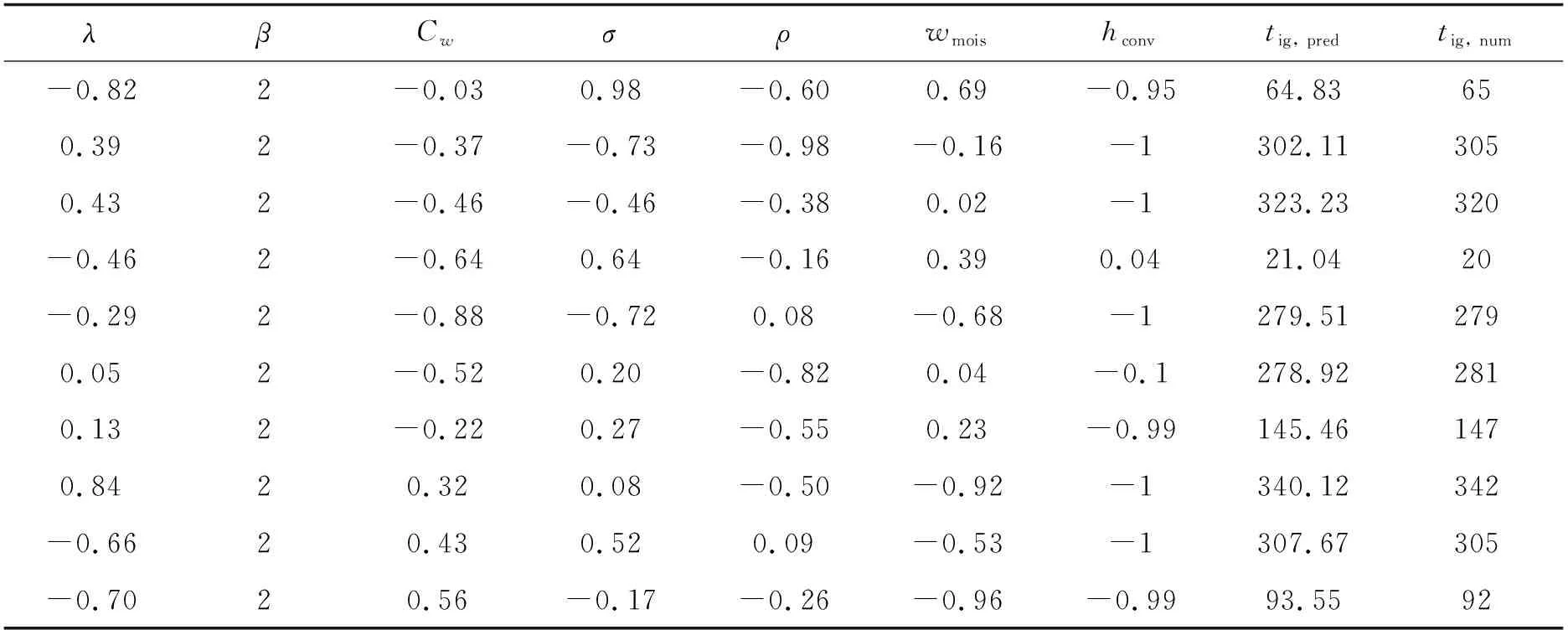
续表1

本文进一步基于ELM开展了参数化研究，分别计算了含水率、比热容及对流系数的影响，计算中其余参数为松木参数，具体见文献[16]，ELM预测结果及数值模型求解结果对比分别如图3～图5所示。由于ELM训练具有随机性，网络最终权值与初始随机权值有关，本文进行了五次训练，并计算了误差棒。图3中含水率从0%到60%时着火时间从88 s变化为134 s。图4中比热容从1 350 J·kg-1·K-1变化至3 000 J·kg-1·K-1时着火时间从92 s变化至105 s。图5中对流换热系数从6 W·m-2·K-1变化至14 W·m-2·K-1时着火时间从97 s变化至102 s。在三种情况下ELM预测结果与数值模型一致，因此与解析公式相比，ELM虽然无法提供各参数关系的显式表达式，但其能够有效获得参数变化时着火时间的变化趋势，为定量理解各参数的影响提供了一种新的研究思路。

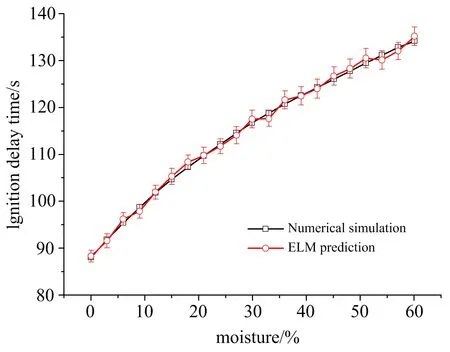
图3 含水率与着火时间关系Fig. 3 Dependence of ignition delay time on moisture

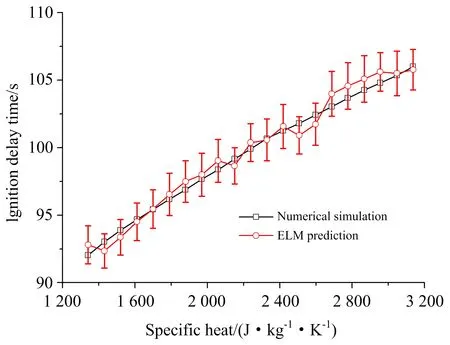
图4 比热容与着火时间关系Fig. 4 Dependence of ignition delay time on specific heat

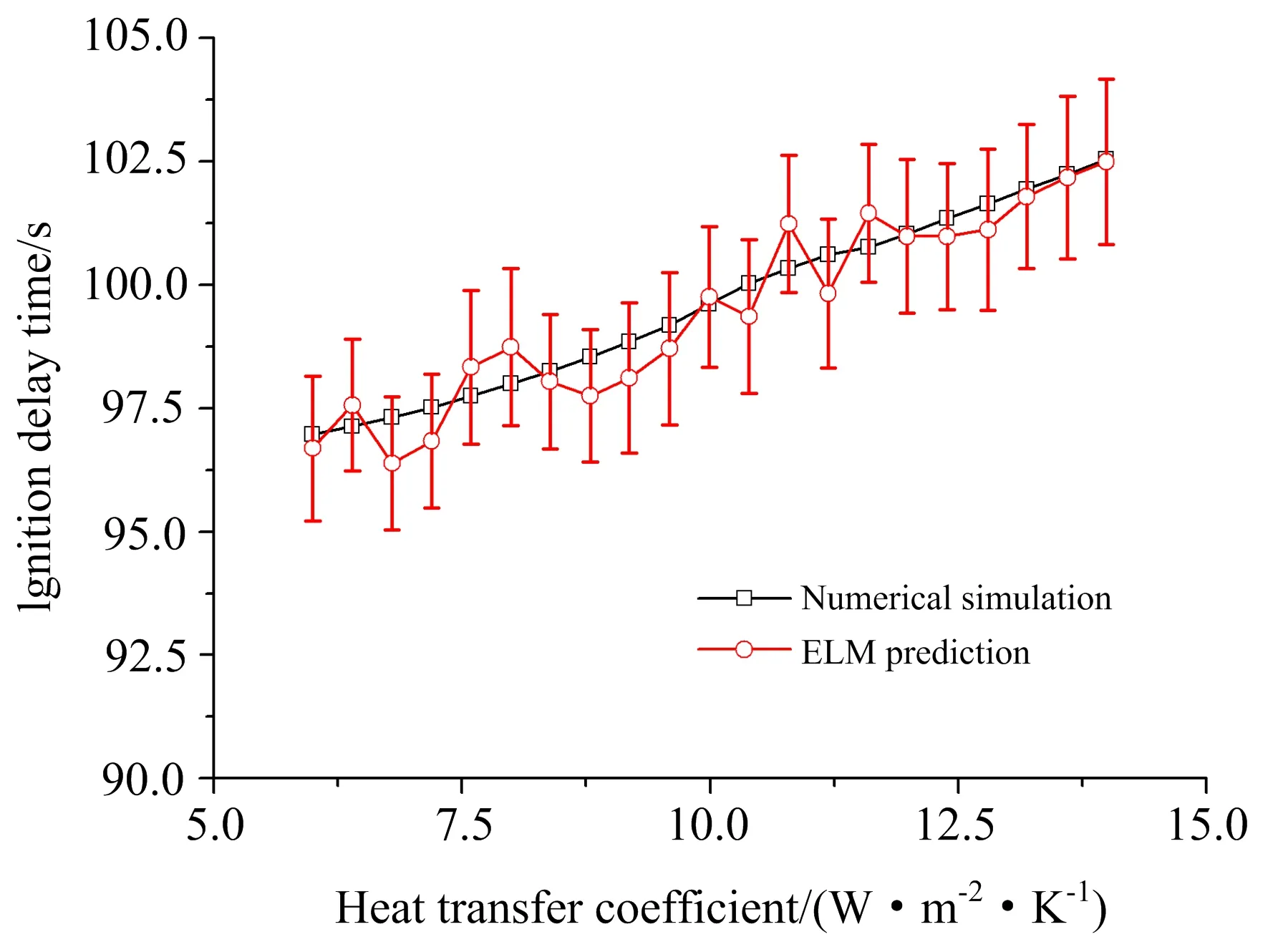
图5 对流系数与着火时间关系Fig. 5 Dependence of ignition delay time on convective heat transfer coefficient

4 结论

针对火蔓延模型中炭化可燃物着火时间快速准确预测的需求，本文提出基于ELM机器学习的方法寻找各参数与着火时间的复杂关系。通过建立炭化可燃物数值模型，考虑水蒸发、热解、热传导等物理化学过程，求解获得不同参数时的着火时间数据，将其代入ELM进行训练验证。结果表明ELM可快速准确获得着火时间，预测平均误差小于3%，低于实验测量不确定度，能够满足一般火蔓延模型要求。同时基于ELM可开展参数研究，快速获得各参数变化时着火时间的变化趋势，从而定量理解各参数影响。相关工作为ELM在热解及火蔓延领域的进一步推广提供了理论与应用基础。