组合赋权的TOPSIS在冲击地压危险性评价中的应用

毕 娟，李希建

(1.贵州大学 矿业学院，贵州 贵阳 550025； 2.复杂地质矿山开采安全技术工程中心，贵州 贵阳 550025；3.贵州大学 瓦斯灾害防治与煤层气开发研究所，贵州 贵阳 550025)

冲击地压是威胁煤矿安全生产的主要灾害之一，其是由于井巷或周围的煤岩体，在达到弹性能量极限时突然释放，而造成猛烈破坏的一种煤岩动力现象[1]。冲击地压发生时还可能引起其他矿井灾害事故，如粉尘爆炸、煤与瓦斯突出及破坏通风系统等，强烈的冲击地压甚至会造成地面建筑设施的破坏[2]。引起冲击地压发生的因素较多，且具有不可预测的特点，导致对冲击地压的危险性评价会非常困难。

目前，国内学者对冲击地压的研究主要集中在冲击地压发生机理和冲击地压治理措施方面[3-4]，而对于冲击地压风险性的评价则较少，主要集中于以经验和现场监测为主的研究，如经验类比分析法和现场实测法[5-7]。随着对冲击地压研究的深入，遗传神经网络算法[8]、突变级数法[9]、未确知测度理论[10]、模糊综合评判法[11]等方法，越来越多地被应用于预测冲击地压危险性和判断冲击地压危险性等级方面。但影响冲击地压的因素有效益指标和成本指标，仅考虑某一因素来评价冲击地压危险性是不够全面的，且冲击地压的发生存在偶然性，在冲击地压危险性评价过程中很难精确预测和描述冲击地压的等级。

鉴于此，在上述研究成果的基础上，建立组合赋权逼近理想解评价模型，分析冲击地压的危险性。首先确定影响冲击地压危险性的主要因素，建立冲击地压评价矩阵，并对原始数据进行预处理，分别利用熵权法和指标相关性确定法计算出各指标权重，根据组合赋权的特点，得出熵权法和指标相关性的偏好程度系数，确定组合赋权的冲击地压权重；其次对正指标和负指标进行处理，确定指标的最优解与最劣解；然后确定待测评对象与最优解、最劣解的距离，得出评价对象的相对贴近度，最终确定冲击地压风险性评价等级。

1 评价指标的组合赋权

1.1 熵权法确定指标权重

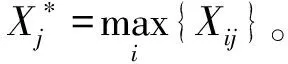
(1)

式中：Xij为不同评价地点的评价指标；Yij为经过标准化处理后的Xij；m为评价地点；n为评价指标。

设第j个评价指标的熵值ej为：

(2)

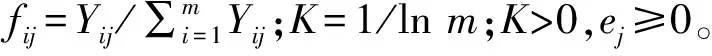
由于0≤fij≤1，所以0≤ej≤1，得到所有评价指标的总熵为：

计算指标j的偏差度dj，dj=1-ej，则评价指标j的熵权ωaj为：

(3)

1.2 CRITIC法计算指标权重

指标相关性的权重确定法(CRITIC)是基于评价指标间的相互对比和不同待测对象间的矛盾性来确定的[14]。利用该方法确定权重，不但考虑了不同指标所含信息量的大小，还考虑了不同方案之间的对比度及冲突性，使评价更加客观合理。

由标准矩阵可得各指标数据的标准差和指标间的相关系数为：

(4)

ρcd=cov(Yc,Yd)/(ScSd)，j=1，…，c，d，n

(5)

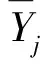
(6)

1.3 组合赋权(CW)确定指标权重

根据熵权法和CRITIC法计算出的各指标权重，建立优化决策矩阵。设组合赋权为ωj，得到CW为：

(7)

式中α和β分别表示熵权和指标相关性权重确定法的偏好程度系数。

根据欧氏距离函数D(ωaj,ωbj)，明确熵权和CRITIC权重的偏好系数[15]，建立差异程度方程：

(8)

联立式(7)和(8)，可得理想组合权重ωj。

2 组合赋权逼近理想解模型

2.1 构造初始评判矩阵

逼近理想解(TOPSIS)是根据各规划方案与理想解的距离大小实现对各方案的评价与排序[16]。

构建CW组合赋权逼近理想解冲击地压模型，设待评价方案集为Ai={a1,a2,…,am}，(i=1,2,…,m)；冲击地压评价指标集为Xj={x1,x2,…,xn}，(j=1,2,…,n)；冲击地压危险性等级为N={N1,N2,N3,N4}，由此可构建初始评判矩阵X。

2.2 加权标准化决策矩阵

将决策矩阵进行归一化处理，依据指标对冲击地压危险性的影响分为正指标和负指标分别计算。

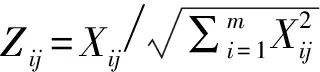
(9)

(10)

根据冲击地压评价指标CW组合权重ωj，建立加权标准化决策矩阵Z*，Z*=(zij)m×n。

2.3 评价对象贴近度

确定最优解C+和最劣解C-：

(11)

式中：C+为最优解；C-为最劣解；J1为正指标集，J2为负指标集。

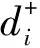
(12)

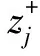
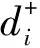
3 实例应用

以文献[17]提供的重庆砚石台煤矿数据为例，该煤矿多次发生特殊动力现象，冲击事故频发，最小的冲击地压煤岩喷出量小于0.5 t，最大的冲击地压煤岩喷出量超过500 t。冲击地压类型与发生地点多样化，冲击地压和瓦斯突出常常同时发生，给煤矿生产和职工生命财产造成极大威胁。随着煤矿开采深度不断延伸，尽管采取了许多冲击地压防治措施，但冲击地压的次数和严重程度并没有得到有效控制，因此确定冲击地压主要影响指标具有重要意义。

3.1 冲击地压评价指标确定

砚石台煤矿冲击地压评价指标按照属性划分为矿山地质因素和开采技术条件两方面。根据矿井实际情况，将冲击地压的评价指标优化为10个指标。影响冲击地压的因素如图1所示。

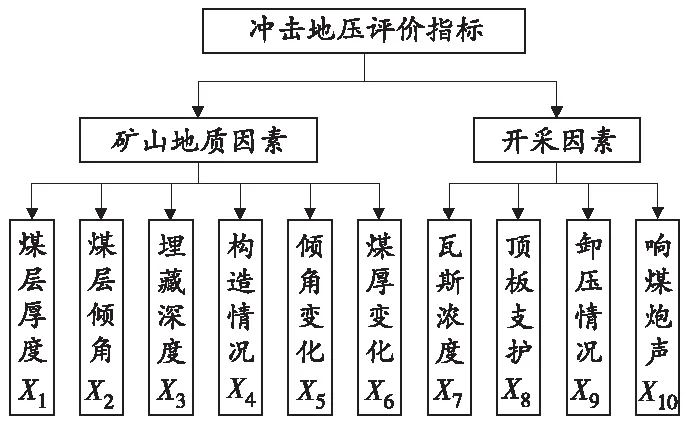
图1 冲击地压评价指标

煤层埋藏深度越大，煤层越厚，越容易积蓄能量，冲击地压动力现象加剧，发生冲击危险性也就越大；煤层倾角越大的倾斜或急倾斜煤层，工作面煤体积蓄的能量也就越多，煤层倾角变化幅度大的区域，地质构造比较复杂，应力集中程度较大，发生冲击危险性也越大。

放炮产生震动，改变了煤体的应力状态，原有平衡被打破，易诱发冲击地压的发生。顶板可以积蓄大量的弹性能，受到采动影响时，顶板弹性能就有可能突然释放，原有应力平衡被打破，发生冲击危险的可能性增大。若顶板支护情况好，冲击地压发生的可能性较小。顶板卸压情况反映了冲击地压防范措施实施的效果，许多重大冲击地压事故的发生，往往是由于没有采取有效的顶板卸压措施。

3.2 原始数据样本

选取砚石台煤矿20组冲击地压样本数据，进行组合赋权耦合逼近理想解的评价，对样本进行量化分析，结果如表1所示。

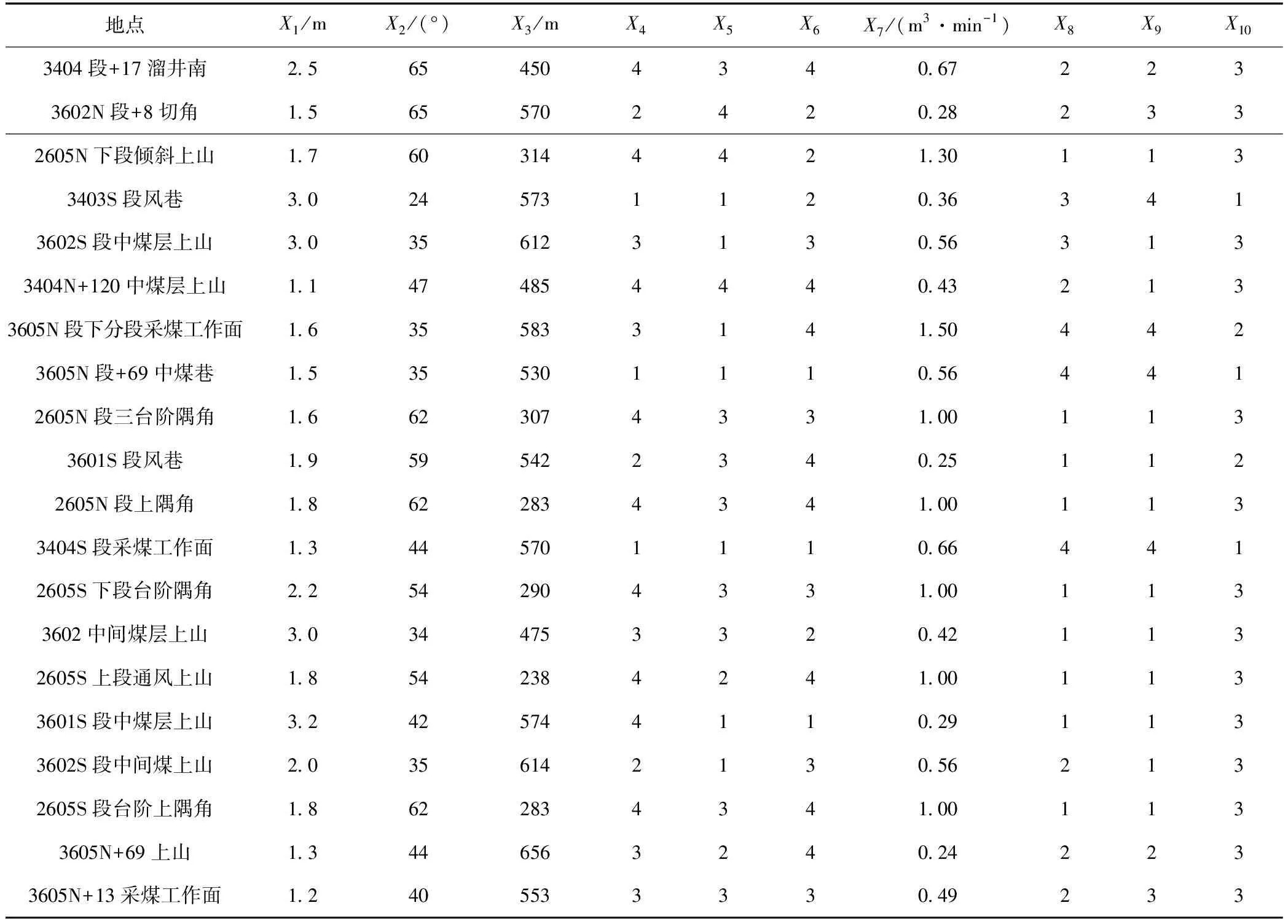
表1 冲击地压危险性评价样本数据

3.3 冲击地压组合权重

根据CRITIC法确定各标准矩阵的协方差，结果如表2所示。并由此得出各评价指标的权重，结果如表3 所示。

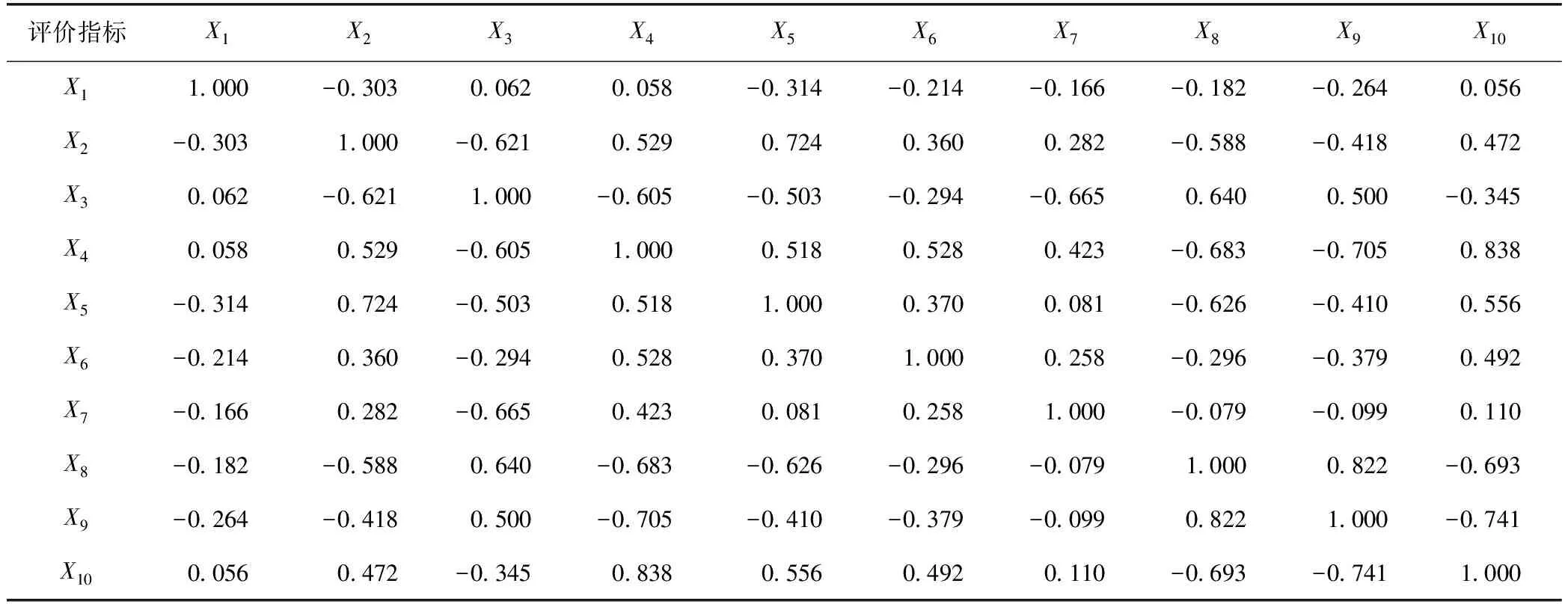
表2 CRITIC法确定各标准矩阵的协方差

表3 各评价指标的权重

根据熵权的原理，确定砚石台煤矿各评价指标的权重。先确定各个指标的熵值，再由式(3)计算得出各评价指标的熵权，结果见表3。根据得出的各指标熵权和CRITIC权重，利用组合赋权的特点，计算熵权和CRITIC法的偏好程度系数α和β，由式(7)和(8)计算得出，α=0.460，β=0.539 9。利用偏好程度系数结合熵权和CRITIC权重，确定冲击地压各指标的理想组合权重，结果见表3。

3.4 冲击地压最优解与最劣解

X8和X9是效益性正指标，最优解是标准化决策数据的最大值，最劣解是标准化决策数据的最小值；其余指标为成本型负指标，最优解是标准化决策数据的最小值，最劣解是标准化决策数据的最大值。由此可确定各评价指标的最优解与最劣解，如表4所示。

表4 各评价指标的最优解与最劣解

3.5 冲击地压相对贴近度

不同等级冲击地压的相对贴近值，如表5 所示。

表5 不同类型冲击地压的相对贴近值

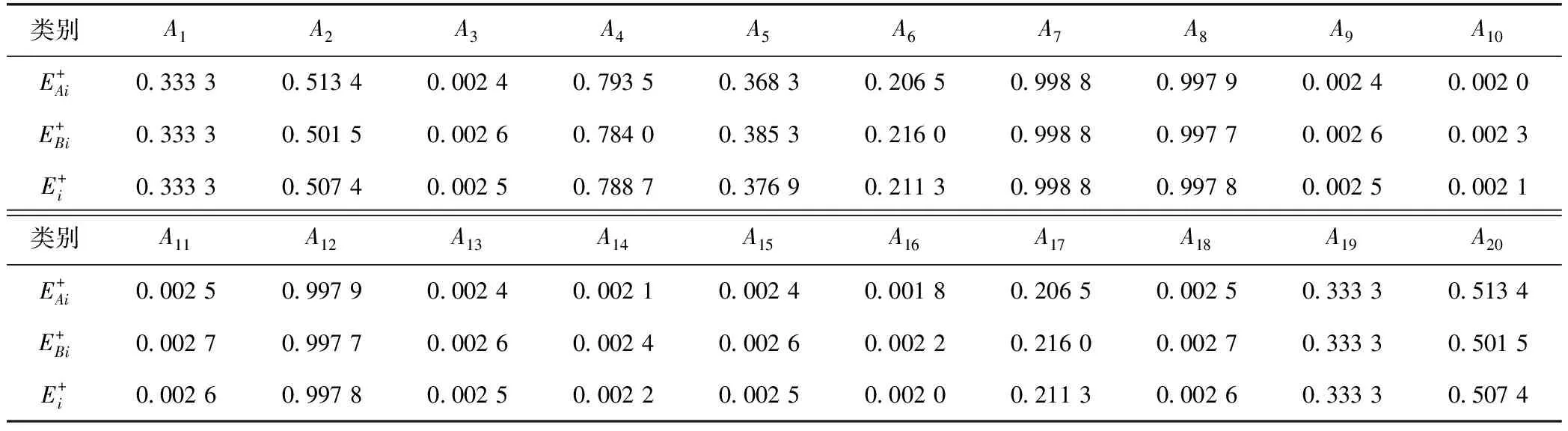
表6 3种模型的相对贴近度

由表6可知，A4、A7、A8、A12属于微冲击地压，煤体发生变形，没有明显的煤岩倾出现象，或煤岩倾出量少；A2和A20属于弱冲击地压，煤岩倾出21 t，采煤工作面响煤炮声不断，由于支护情况好，仅有少量煤岩倾出；A1、A5和A19属于中等冲击地压，喷出煤岩40～100 t，喷出距离10～20 m，堆积坡度12°～17°，并伴随较强的瓦斯突出，可能会造成人员伤亡；其余皆属于强冲击地压，喷出煤岩380～430 t，喷出距离 20 m，堆积坡度10°～25°，极易造成人员伤亡。

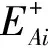
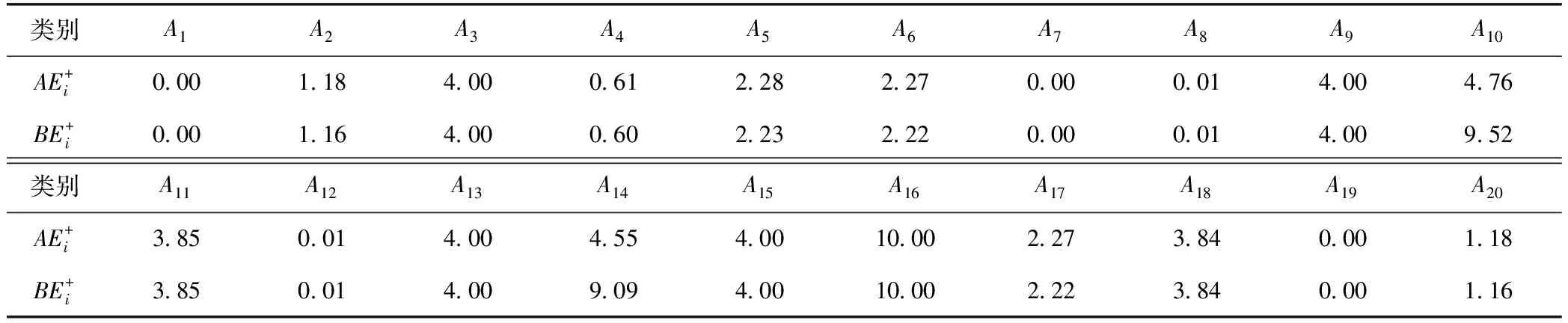
表7 组合赋权逼近理想解的相对贴近度提高精度

由表6、表7可知，组合赋权—逼近理想解的冲击地压模型比熵权—逼近理想解模型的相对贴近度精度平均提高了2.64%；组合赋权TOPSIS的冲击地压模型比CRITIC—逼近理想解模型精度平均提高了3.10%。由此可得，组合赋权—逼近理想解模型评价冲击地压危险性相对误差较小，具有良好的评价准确性，适用于冲击地压危险性评价研究。

4 结论

1)从矿山地质因素和开采因素两个方面确定10个主要影响冲击地压危险性的因素，再根据组合赋权的特点确定指标的综合权重，使得评价冲击地压危险性更加准确。

2)利用逼近理想解对矿山冲击地压危险性进行预测，计算各个评价方案与两个理想解的距离，确定矿井各地点的冲击地压危险性等级。

3)采用组合赋权—逼近理想解模型对重庆砚石台煤矿进行冲击地压危险性评价，并与熵权—逼近理想解和CRITIC—逼近理想解进行对比，精度分别提高了2.64%和3.10%，表明该模型是合理可行的。