基于新距离测度的IGOWLA算子区间组合预测模型

章琛

摘要：在对区间数的预测过程中，由于不确定因素，采用单一的预测方法可能会产生较大的误差的不足;与此同时每种单项预测方法在各个时点处的精度也不尽相同，定权系数区间组合预测模型存在着权重固定不变这一不足之处。本文引入诱导广义有序加权对数平均（IGOWLA）算子，以区间数距离作为最优准则，构建一种基于新距离测度的诱导广义有序加权对数平均算子区间组合预测模型。实例验证表明，本文所构建的区间组合预测方法可提高预测精度，即本文所提出的方法是一种有效的优性的组合预测方法。

Abstract： In the process of interval number prediction， due to the uncertain factors， a single prediction method may produce a large error. At the same time， the accuracy of each single prediction method at each time point is not the same. There is a shortage of fixed weight in the interval combination forecasting model with fixed weight coefficient. In this paper， the IGOWLA operator is introduced， and the interval distance is used as the optimal criterion to construct an interval combination forecasting model based on the new interval number distance measure. The example shows that the interval combination forecasting method can improve the forecasting accuracy， that is to say， the method proposed in this paper is an effective combination forecasting method.

关键词：区间组合预测;区间数距离测度;诱导广义有序加权对数平均算子

0  引言

“凡事预则立，不预则废”，但由于不确定因素，导致单项预测方法在预测过程中很有可能会产生较大的误差。组合预测是对各种单项预测方法进行综合集结的一种方法，能够获得更高的预测精度和更好的预测效果。在客观世界中，环境的不确定性，使得给出预测信息不能准确确定，这时可以用区间数进行描述。因此在基于组合预测模型的基础上，对于模糊环境下经济变量进行区间数组合预测的研究具有极其重要的意义。

为了避免单项方法预测时可能产生的不足，将各种不同单项方法中所能提供的有效信息尽可能的利用起来，学者 Bates J.M.和Granger C.W.J.（1969）首次对组合预测方法进行系统研究，随后学者Yager（1988，2004）提出了有序加权平均算子和广义诱导有序加权平均算子的有关内容。近几十年来的国内，也有很多学者关注组合预测方法。唐小我（1991）提出确定组合预测加权系数的计算方法;陈华友教授（1998）研究有关变权重且为非负情况下的组合预测模型并提出了详细的计算过程，提出了多种相关指标用来作为最优准则;杨桂元教授（1998）提出了基于折扣系数法的组合预测模型同时研究了非负加权系数的最优组合预测方法。当然，区间数方面的研究也应运而生，周礼刚等（2010）和林义征等（2016）通过引入向量夹角余弦的精度指标并将其作为最优准则，建立区间型组合预测模型;周礼刚等（2010）和周远翔（2016）将灰色关联度作为最优准则，建立区间型组合预测模型并和单项预测方法效果对比;胡凌云等（2018）则将区间数距离作为最优准则，建立区间型组合预测模型。

根据以上有关文献对于组合预测模型的研究，本文在此基础上采用了一种新的更为合理的距离计算方法来测度实际区间与预测区间间距离，通过引入IGOWLA算子，建立实际区间与预测区间间距离最小的变权组合预测模型，并用实例来分析验证本文方法的有效性、合理性。

1  基于新距离测度的IGOWLA算子区间组合预测模型

①得到的每个单项预测区间数序列为：

②m种不同单项预测方法在组合预测中的对应的权系数应满足各项在0-1之间且所有项之和为1。

③将m种不同的单项预测方法组合而成的组合预测区间数最终结果记为：

1.1 构建由IGOWLA算子集结而成的组合预测区间数

1.3 构建基于新距离测度的IGOWLA算子区间组合预测模型

1.4 构建区间组合预测模型的检验与评价指标体系

选取平均区间位置误差平方和（MSEP）、平均区间长度误差平方和（MSEL）、平均区间误差平方和（MSEI）以及平均区间相对误差和（MRIE）作为区间型组合预测效果的评价指标体系。其中，当这些指标对应的数值越大，则预测效果越无效;当这些指标对应的值越小，则预测效果越有效。

2  实例分析

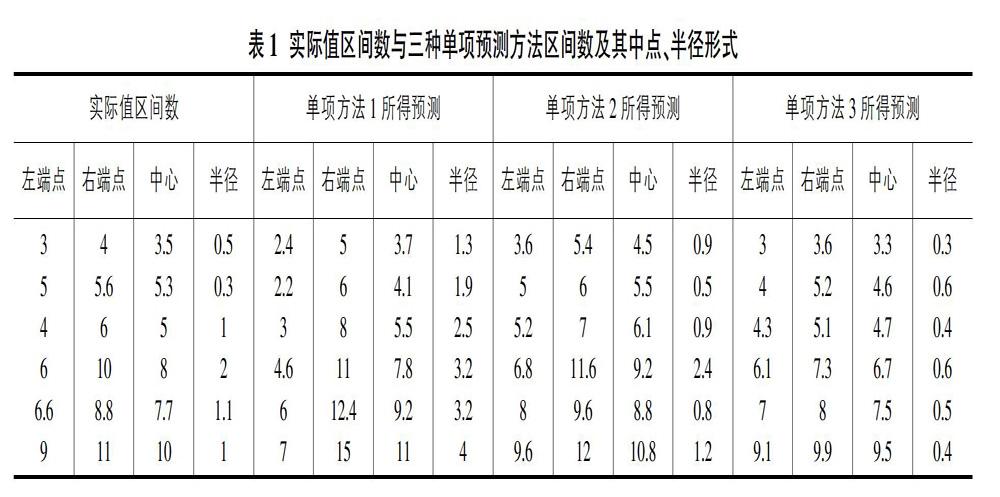
本文将选取文献[7]中的数据用于验证模型（I）的有效性，其具体预测区间数数据如表1所示。

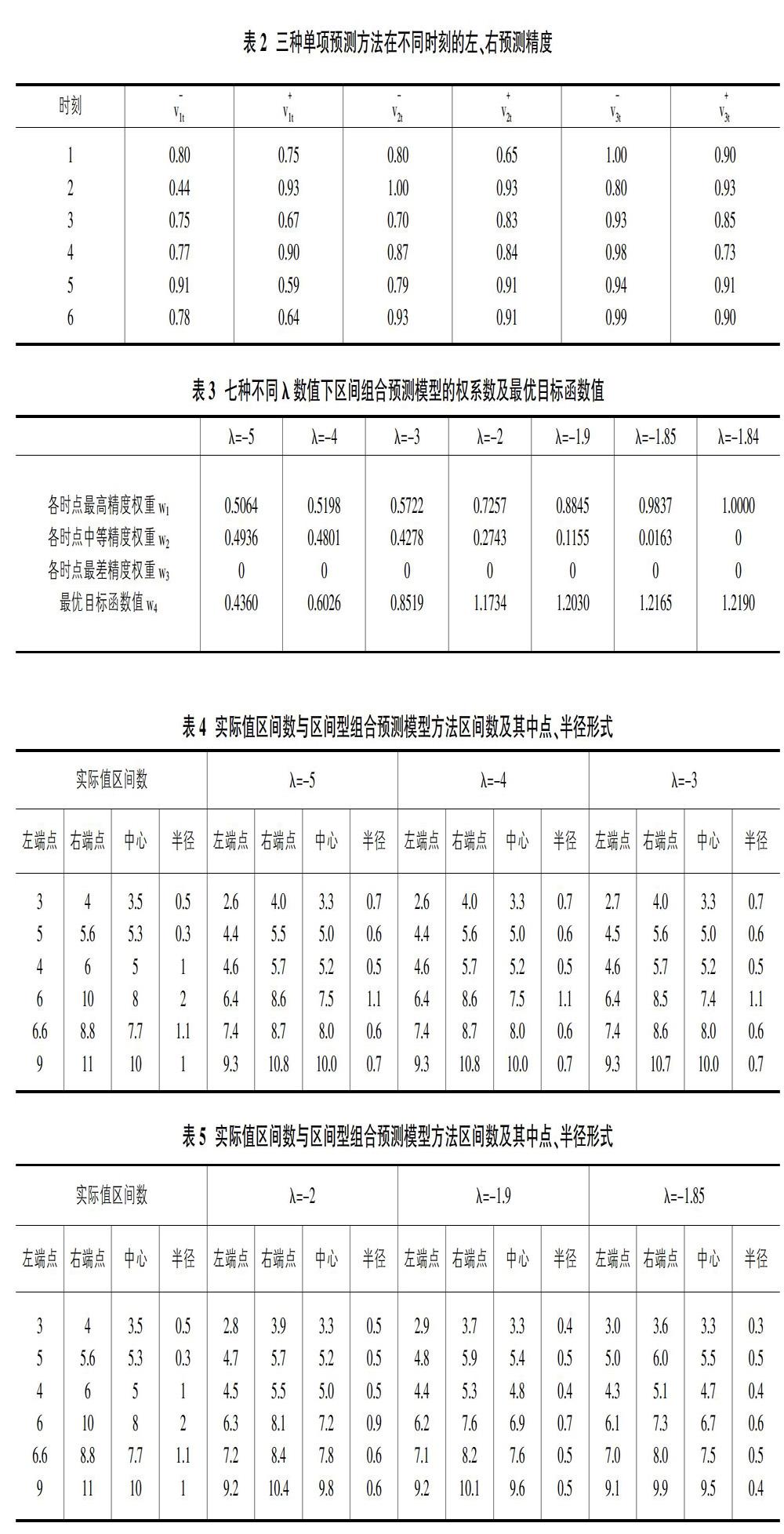
根据表1中各项数据，计算出每種单项预测方法对应在不同时刻的预测精度，其中第i（i=1，2，3）种方法在t（t=1，2，，3…6）时刻的左、右精度上标分别为负和正，所得结果如表2所示。

将表2和表1中的数据带入模型（I）中，因参数值是任意非数，故为方便计算，分别在整数和负数范围内取不同且互为相反数的数值，结果发现当参数值大于0时，不存在可行解;当参数值小于0时，利用LINGO软件求解当分别取不同值时，得到的最优权系数及最优目标函数值的结果如表3所示。

根据不同情况下的不同权重，可以计算出每种情况下的组合预测区间数结果，结果如表4、表5所示。

利用区间组合预测模型的检验与评价指标体系，对本文所建立的基于新距离测度的IGOWLA算子区间组合预测模型（I）的预测结果进行评价，结果如表6所示。

3  灵敏度分析

观察本文选取的六个不同的参数值所对应下的模型（I）的各项误差指标，发现这些指标值是都小于只使用单项预测方法时的误差指标值得。也就是说这些不同？姿的参数值所对应下的组合预测模型的误差指标均为最优，不同参数值所对应下的模型（I）的有效性影响均是很显著的，故对以上不用参数值下的模型（I）对应的权重值、目标函数值以及误差指标值进行进一步分析研究。

根据表3所示结果可以做出各时点最高精度权重、各时点中等精度权重的趋势变化图，如图1所示。

可以明显看出最高精度权重始终大于中等精度权重以及最差精度权重（恒为0）。其中，最高精度权重随着参数值从-5到-1.84变化时，整体呈现上升趋势，直到达到1.0的水平，且每种情况下都在0.5之上;而随着参数值从-5到-1.84变化时，整体呈现下降趋势，直到达到0的水平，且每种情况下都在0.5之下。

根据表3中的目标函数值，描绘当参数值从-5到-1.84变化时其变化情况，结果如图2所示。可以看出，当参数值为-1.84时目标函数值都取最大值，对比三种不同的原始的单项预测方法，进而可以说明在这几种参数值情况下的组合预测方法都是优性的。

本文通过将所得基于新距离测度的IGOWLA算子区间组合预测模型（I）中参数值取不同数值之时与三种单项方向、基于IOWA的方法和基于IOWC-GOWA算子的方法进行比较，根据表6中的相关数据，可以很清晰地看出：当参数值从小到大时，四个评价指标的数值先是缓慢降低，即模型（I）的效果先缓慢地逐渐变得显著，均在参数值为-3时达到最小值，分别为：0.0855、0.1879、0.2734和0.1795;接着在参数值为-3时开始转向，转而迅速上升，即其预测效果紧接着快速回落到低水平，但都比三种单项方向、基于IOWA的方法和基于IOWC-GOWA算子的方法效果更好。

4  结束语

本文引入IGOWLA算子，以区间数距离作为最优准则，构建基于新距离测度的诱导广义有序加权对数平均算子区间组合预测模型。实例验证表明，本文构建的区间组合预测方法可提高预测精度，即本文所提出的方法是一种有效的优性的组合预测方法。但在模型的分析过程中，本文的不足之处在于没有讨论所有参数变化情况下的模型的预测效果，因此今后将研究其他参数取值对本文提出模型的预测结果的影响来完善此模型。

参考文献：

[1]陶志富，刘金培，朱家明，陈华友.区间值时间序列预测效果测度研究[J].模糊系统与数学，2018，32（04）：135-144.

[2]胡凌云，袁宏俊，周洁.基于区间数距离的IGOWLA算子的区间型组合预测模型[J].延边大学学报（自然科学版），2018，44（02）：109-115.

[3]周洁.优性区间型组合预测方法及应用研究[D].安徽财经大学，2018.

[4]陈华友，朱家明，丁珍妮.组合预测模型与方法研究综述[J].大学数学，2017，33（04）：1-10.

[5]周远翔，宋马林，袁宏俊.基于灰色关联度的广义IOWA算子组合预测模型[J].统计与决策，2016（09）：86-88.

[6]林义征，袁宏俊，宋马林.基于IOWHA算子与向量夹角余弦的联系数型区间组合预测[J].统计与决策，2016（05）：84-86.

[7]李洪岩，陈华友.基于Theil不等系数的IOWHA算子组合预测模型及其应用[J].数学的实践与认识，2011，41（11）：105-112.

[8]周礼刚，陈华友，韩冰，汪晶瑶，艾全达.基于对数灰关联度的IOWGA算子最优组合预测模型[J].运筹与管理，2010，19（06）：33-38.

[9]周礼刚，赵娟，陈华友，丁子千.基于向量夹角余弦的IOWGA算子组合预测模型[J].合肥工业大学学报（自然科学版），2010，33（09）：1425-1429.

[10]刘华文.基于距离测度的模糊数排序[J].山东大学学报（理学版），2004（02）：30-36.

[11]马永开，唐小我.线性组合预测模型优化问题研究[J].系统工程理论与实践，1998（09）：111-115，124.

[12]馬永开，唐小我，杨桂元.非负权重最优组合预测方法的基本理论研究[J].运筹与管理，1997（02）：1-8.

[13]Bates J M， Granger C W J. Combination of forecasts [J]. Operations Research Quarterly， 1969， 20（4）：451-468.