基于K-means聚类挖掘智能机器人领域技术创新人才

赵宁?赵翀?翟凤勇　刘伟?郭伟

摘 要 以智能機器人领域为例，借助机器学习的方法挖掘技术创新人才，消除专家分类的主观性。通过专利信息构建技术创新人才评价指标体系，结合主成分分析、K-means聚类，进行技术创新人才有效分类;利用DWPI手工代码挖掘智能机器人领域对应的创新人员及相应的技术团队成员，对于技术创新人才分类有进一步优化空间。K-means聚类改进了传统的识别方法，突破人工统计的局限，可以处理数量级更大的数据，对数据挖掘可以进行及时、准确、直观的分析。

关键词 专利信息 聚类分析 技术创新人才 K-means

分类号 G252.62

DOI 10.16810/j.cnki.1672-514X.2020.03.009

Abstract Taking the intelligent robot field as an example， by means of machine learning， the subjectivity of expert classification can be eliminated. The evaluation index system of technological innovation talents is constructed by patent information， and the effective classification of technological innovation talents is carried out by combining principal component analysis and K-means clustering. The corresponding innovation personnel and corresponding technical team members in the field of intelligent robot are mined by DWPI manual code， which has further optimization space for the classification of technological innovation talents. K-means clustering improves the traditional recognition method， breaks through the limitations of artificial statistics. It can deal with larger data of order of magnitude， and can analyze data mining timely， accurately and intuitively.

Keywords Patent information. Cluster analysis. Technological innovative talents. K-means.

专利作为一种标准化、公开透明、客观化的文献，由于其所载信息贯穿科研流程和活动的不同阶段，对技术发明有详细描述，不仅可以从本质上揭示技术创新能力[1]，而且常作为技术创新的重要指标，被嵌入各种技术创新能力量化的评价体系中，以便简化评价流程而得到可靠的评价结果[2]。基于专利文献反映技术创新活动相应的特征，本文拟以智能机器人技术专利文献为例，运用K-means聚类，通过构建专利信息构建技术创新人才评价指标体系，进行技术创新人才有效分类分析，以便于科研管理者或者政策制定者掌握技术人才的优势，进行机构中人员的科学配置，提升机构的科研竞争力。除此以外，还可通过聚类发明人，寻找不同科研层次水平的划分标准，进行技术创新人才聚类，有助于人才所属类型的判断，类似于技术创新人才分析中战略上的规划，不仅可以为国家发掘智能机器人领域的技术创新人才，还可以进行技术战略布局，推动整个智能机器人行业的发展，更能细化申请资助和激励政策，有助于针对性政策的制定[3]。

1 专利信息分析技术创新人才结构及界定

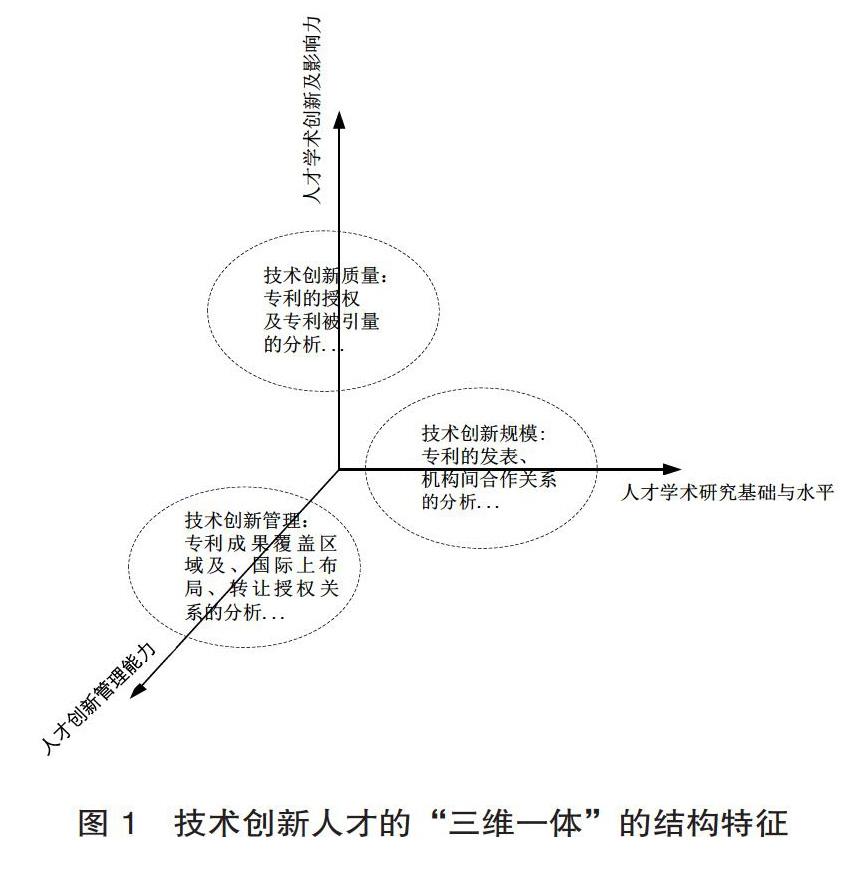
基于专利信息的分析角度，宏观上，可以挖掘技术创新团队，审视发明人在团队中的重要性;微观上，可以判断专利的技术水平，判别发明人的技术创新能力[4]。如结合以往的研究，使用专利数据可衡量地区技术创新现状[5]，从专利数量、发明人角度对高校技术创新进行评价[6];结合合作研究、有效专利年限对高校技术创新能力进行评价[7]。根据专利信息统计所分析的对象不同、目的不同，学者们定义了很多专利信息内容统计指标，从不同角度揭示专利信息内容对应技术创新能力的关系。基于专利信息分析技术创新能力的研究，大多是对技术企业竞争力的分析，而从人才特征来分析挖掘创新能力的不多。基于此，本文拟根据技术创新人才特征，基于专利信息指标与技术创新能力的对应关系，以专利信息为主要数据对于技术创新人才从三个维度界定，提出技术创新人才的“三维一体”结构特征，如图1所示：

2 基于专利分析的技术创新人才评价指标体系

技术创新人才评价指标体系指标的选取，需要从多个层面、多个角度综合地对技术创新能力进行评价。首先基于不同领域技术创新人才能力的考虑，选择相应的分析内容，利用所选评价方法对于专利技术水平评价指标权重设置。其次根据所反映的技术创新人才三维水平结构去设计评价体系，再根据专利信息组合分析的思想将评价指标分为专利数量指标、专利质量指标、专利价值指标，这主要基于发明专利的分析，通过专利指标揭示技术创新信息和水平，如表1所示。

3 基于DI的技术创新人才的专利指标体系

本文选取科睿唯安（Clarivate，原汤森路透公司）的德温特创新平台Derwent Innovation（DI） 数据库作为样本进行分析。该数据库整合了全球专利情报，收录来自全球超过50家专利授予机构（涵盖90多个国家和地区）的专利信息、超过1亿篇专利。对收录的专利文献，由专家进行深度加工改写生成德温特世界专利索引（DWPI），保证检索全面、具有专业权威性。专利发明人的著录方式在不同数据库中有所不同，基本都涉及中国人名和外国人名消歧问题。整体来说，DI数据库的姓名信息完备程度比较高，部分发明人为姓拼音+名首字母缩写，也需要通过数据清理判别是否为同一发明人，比如Jones Joseph L.和Jones JL为同一发明人，因此选取DI专利数据的检索结果，结合科睿唯安的另一款产品德温特数据分析平台Derwent Data Analyzer（DDA）和手工进行数据清洗来分析发明人[12]。

对于技术创新人才的挖掘评价需要有科学性、可测量性、可行性，符合目标管理的原则[8]。结合上述技术创新人才指标体系的研究，基于DI检索及所输出的指标，组合及计算，统计分析发明人的相关可以获得的指标，筛选后的指标构成技术创新人才能力评价体系。这种体系应该是一个多层次的体系，能准确反映技术人才能力的各个方面，如图2所示，包括以下众多元素：第一发明人专利数、专利申请量、专利授权量、专利授权率、专利有效量、专利有效率、国际同族专利数、总共合作其他作者人员数、专利平均合作发明人数、总共合作专利数、IPC大类数、IPC小类数、DWPI分类代码数、被引篇数、被引次数、被引百分比、引证率、H指数、G指数、平均专利权数。符合指标体系优化、相关性、注重专利质量作用、指标有量、有率的科学性原则。

4 基于K-means的聚类分析

用传统的分析方法已经不能处理大量不相关的数据，比如专利信息的不同指标。机器学习是建模隐藏的数据结构，然后做识别、预测分类等。对样本进行挖掘分析，采用根据具体训练数据开展机器学习，进一步获得分类模型，科学划分类别。当前的算法有很多，借助数据挖掘应用算法，进行发明人聚类，其中K-means是用均值算法把数据分类的机器学习算法，从而找到数据变量之间的关系，可以应用于大数据，从而精炼数据。聚类和分类最大的不同在于，分类的目标是事先已知的，而聚类事先不知道目标变量是什么，类别没有像分类那样被预先定义出来，所以，聚类有时也叫无监督学习。通过发明人的专利信息指标统计，指标间有些隐含的相关性，综合多指标对应的数据，属于这种无监督学习，聚类分析试图将相似的发明人归入同一簇，将不相似的发明人归为不同簇，通过此挖掘类似的技术创新人才及技术创新人才团队。

K-means是一种聚类算法，据百度百科介绍这种算法是依赖于点的邻域来决定哪些点应该分在一个组中。当一堆点都靠的比较近，那这堆点应该是分到同一组，将数据分成k个彼此排斥的类，返回分配给每个观察的类的指标，K-means聚类对待数据的每个观测点为一个空间的对象，同类的尽可能靠近，不同类的尽可能远些。可以选择不同的距离测度，取决于要聚类的数据的情况。每个类别被定义为其元素对象和中心点，使用K-means，可以找到每一组的中心点，每个类别的中心点是该类中包含的元素距离之和最小的那个点。当然，聚类算法并不局限于2维的点，也可以对高维的空间（三维，四维等）的点进行聚类，任意高维的空间都可以[9]。K-means算法流程如图3所示。

（1） 从数据集X中，随机选择k个中心点，作为初始聚类的中心;

（2） 针对所有对象的每一个中心距离进行相应的计算计算数据集中每个样本到聚类中心这k个点距离;

（3） 找到每个数据样本到聚类中心的最小距离，并将数据样本归为与相同的类中，即;

（4） 重新计算中心点，调整聚类中心，即将聚类的中心移动到聚类的几何中心（即平均值）处，也就是K-means中的mean含义;

（5） 迭代中心点，重复（2）（3）迭代更新，直到准侧函数开始收敛，所得簇中心不再发生变化或者达到最大运行次数，其中平方误差准则函数计算公式为：

其中J表示所有类中样本对象的平均误差总和，表示第i类中的聚类中心点，表示第i类中的样本对象。

（6）假设我们已经通过K-means，将待分类数据进行了聚类，将待分类数据分为了k个簇。对于簇中的每个向量。分别计算它们的轮廓系数，轮廓系数（Silhouette Coefficient）结合了聚类的凝聚度（Cohesion）和分离（Separation），用于评估聚类的效果。该值处于-1～1之间，值越大，表示聚类效果越好。具体计算方法如下。

对于每个i来，计算i与同簇其它点的距离，记做a（i），选取i外的一个簇b，b（i）=min（i到各非本身所在簇的所有点的平均距离）

那么 i 向量輪廓系数就为：

将所有点的轮廓系数求平均，就是该聚类结果总的轮廓系数。在实际应用中K-means一般作为数据预处理，k不会设置很大，通过枚举，k从2到固定值，在每个k值上重复运行次数K-means，并计算当前轮廓系数，最后选择轮廓系统最大的值作为最终簇数。

5 智能机器人领域技术创新人才检索与挖掘

5.1 智能机器人专利信息检索

在概念界定上，大多数专家认为，智能机器人不完全依赖人类的操作，具有对语音、行为、姿势等感知、识别、交互能力，如移动机器人、服务机器人和仿人机器人等的自控机器人具有自主性、自适应、自学习、自感应，可以强化学习、深度学习，进行路径跟踪、路径规划、位置识别、智能导航……另外，智能机器人在结构上具有手眼协调、双臂协调的特色，主要的关键技术有多传感器新信息融合、超声波传感器……[10-12]，根据这些特点将关键词及同义词，进行测试组合形成检索式，采用Dewent Innovation（DI）数据库进行检索，结合关键词在数据库测试的结果，最终利用专家检索，通过位置运算符的关系进行以主题字段检索，其检索式如图4所示。

检索截止时间为2018年8月19日，20 620个记录经过选取DWPI同族专利归并方式去重得到12 335个专利族，通过字段KI=（a or a1 or a2 or b or b1 or b2 or c） 筛选发明专利得到9241个专利族。

5.2 挖掘技术创新人才的过程

根据莱斯定律，选取评价分析的发明人的数量由各专利发明作者总数（未进行算法分析和人工校对）的平方根来大致决定，即每个专利发明人总数的平方根决定入选技术创新人才所需的数量的阈值，这里不到10 000个专利，选取第一发明人为主要分析对象，除去重复的，肯定是小于平方根100，所以对申请量排名前100个发明人进行指标分析即可挖掘出该领域的技术创新人才。选取2001—2018年DI专利数据的检索结果，对发明人数据进行清洗和专利信息各项统计，得到原始专利指标样本——申请量排名前100的发明人专利指标数据。专利信息数据处理方法如图5所示。

对于智能机器人领域技术创新人才的挖掘，根据统计的专利信息指标数据做进一步研究，围绕发明人的18维指标进行分析，利用主成分分析找到评价发明人的重要指标，并通过K-means自动聚类技术创新人才。K-means 算法主要采用欧式距离来度量各个簇间的相似性，然而对于数据间的相关性并没有被很好的展现出来，因此同时结合PCA将可能相关的变量处理为线性不相关的，以解决类别相关性影响。

6 基于专利信息指标发明人聚类处理与分析

6.1 专利信息数据标准化处理

为了消除专利信息指标之间的量纲影响，便于综合分析，对初始数据每列减去该列均值，再除以样本方法进行Z-Score标准化。

其中是原始数据的均值，σ是原始数据的样本方差

将不同量级的数据转化为统一量度的Z-Score分值，消除量纲影响，如图6箱型图所示。

箱型图的以一种相对稳定的方式描述数据的离散分布情况，通过图6可以发现，专利发明人在每个评价维度的分布并不对称，且出现右尾偏离的特征。其中合作专利数、被引次数、引证率、国际同族专利数等评价指标，多数分布范围较小，但同时异常值也较多，相应的评价权重应该较大。

6.2 主成分分析重要性指标

发明人技术创新能力受多因素影响，基于专利信息提取的评价指标比较多，每个专利指标在不同程度上反映了技术创新的信息，而主成分分析PCA（Principal Component Analysis） 是用较少的新特征的线性组合代替旧特征，并且新特征之间互不相关，尽可能减少消除评估指标之间的相关影响，利用较少的综合指标来反映各指标间的变化，并减少信息损失[13]。定义原始矩阵，由专利评价指标数组成，样本为待评价的发明人。根据18个专利信息指标的相关系数矩R，计算特征值和特征向量，计算主成分贡献率和累加贡献率，由主成分载荷计算得分，通过主成分的进行加权求和计算得分，从而对样本即发明人进行评价。具体计算得到的分值如表2所示。

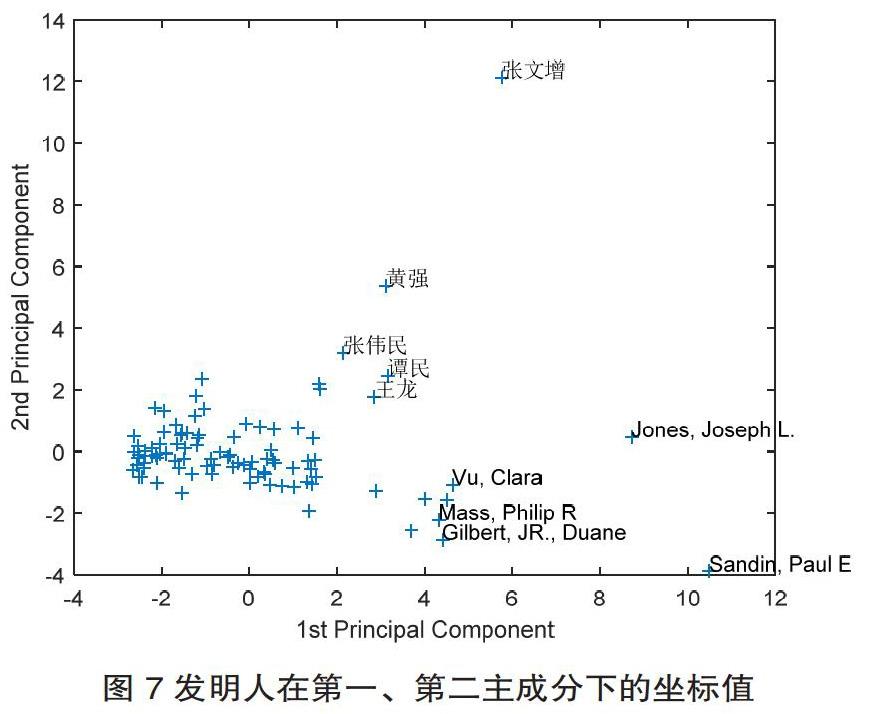
其中，最大相关系数竟高达0.949，表明这些评价指标中有些高度相关，适合主成分分析。经过主成分变换，在发明人第一、第二个主成分下的分布，绘制图形如图7所示。

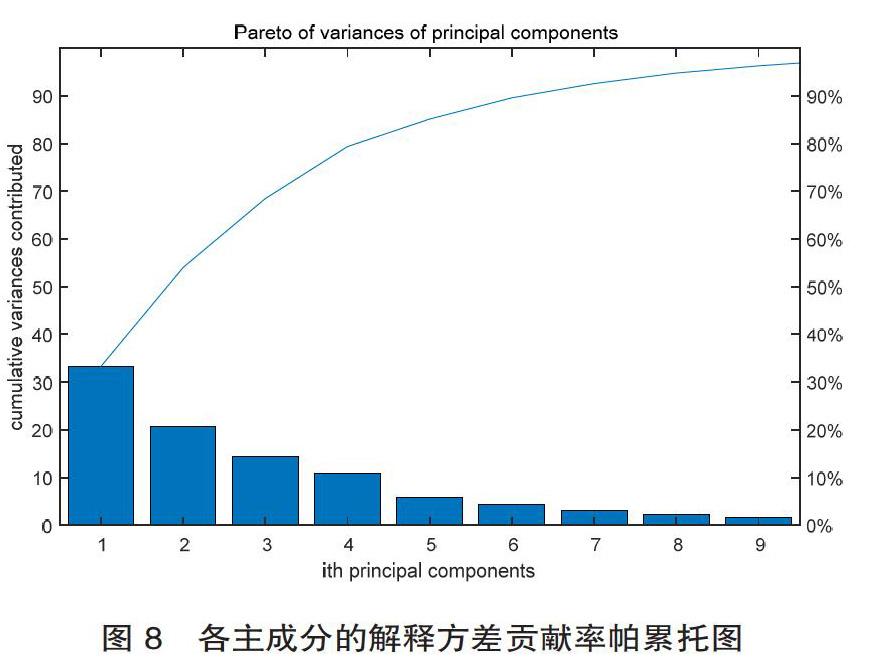
各主成分对应的方差解释贡献率的帕累托图，如图8所示。

从图8可以看出，前5个主成分已经足够解释数据的变换（累计方差贡献率为82.47%），因此选用前5个主成分，可以对原来的数据进行降维。前5个主成分对应的系数矩阵为表3。

根据线性变换的思想，通过累加贡献率选出重要成分，化简变量，从而揭示新的变量间的关系。由该表可以看出，前5个主成分对应各指标的最大系数，分别是H指数、申请量、IPC小类、平均发明人数、专利有效率。H指数代表了技术创新质量，反映的是发明人的影响力;专利申请量代表了技术创新规模，反映的是发明人的技术创新投入、规模和活跃度;IPC小类代表技术创新的覆盖范围，反映技术创新规模;专利平均发明人数，反映技术创新人才协同的能力;专利有效率代表技术创新管理水平，反映发明人的核心竞争力;平均专利权代表专利的技术特征、技术含量、覆盖范围，也是反映技术创新质量的重要指标。这5个主成分的最大荷载变量在一定程度上也说明了这些因素对评价专利发明人的重要指标。

6.3 K-means具体计算过程及结果讨论

根据100组发明人专利信息指标数据，根据前面计算的主成分分析，选取前5个主成分，对100组观测值的前5个主成分矩阵Z，进行K-means聚类算法。由于K-means聚类算法涉及一个非线性规划求解，为避免限于局部极小值点，随机生成初始解，重复1000次，选取误差指标最小的为K均值聚类。

若分成三类，四类，五类，则对应的轮廓值silhouettevalue分别为图9-图12。

根据K-means理论，轮廓值整体大于或等于0且与1的距离接近，聚类效果较好。因此，根据前面各图的轮廓值整体状况，确定聚类数为4，为一个恰当的选择。在第一、第二个主成分图形中，100个发明人绘制的分类情况如图12所示。

三类和四类的往往对应着分值较高的发明人，他们的综合评价指標结果类似，比如Vu Clara、Mass Philip R、Ozick、Gilbert JR. Duane类;黄强、张为民、余张国类综合指标接近，科研层次水平接近，可能为一个技术创新团队中，通过K-means进行技术创新人才聚类，判断技术创新人才所属类型的。

6.4 智能机器人领域技术创新人才分析结果

结合DDA的发明人-DWPI手工代码共现进行智能机器人领域技术创新人才挖掘分析，美国iRobot公司的创新团队主要为Sandin Paul E和Jones Joseph L组成，其成员包括Vu Clara、Mass Philip R、Ozick  Daniel N、Mack Newton E、Nugent David M、Lynch James，Cohen David A和Gilbert JR. Duane也是该公司可以挖掘的创新人才，通过分类代码聚类得出其主要研究方向集中于除尘机器人领域上;国内智能机器人领域主要创新人才有清华大学张文增，其研究领域主要在机械手的研究上，其团队包括陈强;在计算机与程序控制机机器人主要技术领域上，挖掘到美国iRobot公司的Cohen David A，中国科学院自动化研究所谭民、北京理工大学的黄强、国家电网山东鲁能技术有限公司的韩磊、浙江大学熊蓉技术创新人才，其他人才挖掘信息总结见表4所示。通过K-means聚类结果可以反映技术创新人才的类别，结合分析，聚类多是同一技术创新团队的人才。

7 结语

通过机器学习方式将对统计的专利信息指标数据进行数值标准化变化处理，消除量与率上的影响，用K-means结合PCA将可能相关的变量处理为线性不相关的，解决了类别相关性影响，聚类结果可以反映技术创新人才的类别，结合技术代码分析，从而聚类挖掘到智能机器人领域技术创新人才。K-means聚类是探索性数据挖掘中的一种常用方法，是对大量无序的数据集，按数据的内在相似性将数据集进行聚类，更好地理解研究对象的目的。将K-means聚类引入技术创新人才挖掘，较之以往的方法，在传统识别方法上有一定程度的改进，忽略内部关系的情况下通过非线性映射实现高精度输出，机器学习、非线性、动态，突破人工统计的局限，可移植其他系统操作，可以处理大于100数量级的更多的大数据，进行及时、准确、直观地分析。

参考文献：

鲍志彦.高校技术创新能力评价实证研究：基于专利信息的测度分析[J].农业图书情报学刊，2016，28（8）：5-10.

曹明，陈荣，孙济庆等.基于专利分析的技术竞争力比较研究[J].科学学研究，2016，34（3）：380-385，470.

王韬，王晓毓.基于数据挖掘的高校人才科研能力培养策略探究[J].当代教研论丛，2016（5）：138.

JUNGA S， IMM K Y. The patent activities of Korea and Taiwan： a comparative case study of patent statistics[J].World Patent Information，2002，24（4）：310.

LACH S. Patents and productivity growth at the industry level： A first look[J].Economics Letters，1995，49（1）：106.

李文辉，贺浪萍，林卓玲.从国内专利角度分析华南师范大学的技术创新能力[J].华南师范大学学报： 自然科学版，2011（2）：141.

应璇，孙济庆.基于专利数据分析的高校技术创新能力研究[J].现代情报，2011，31（9）：168.

方曙.基于专利信息分析的技术创新能力研究[D].重庆：西南交通大学，2008.

百度百科.K-means[EB/OL].[2018-11-20].https：//baike.baidu.com/item/K-means/4934806.

AUSTIN，陈勇.智能机器：区分事实与虚幻[J].电子产品世界，2016，23（10）：7-7.

WEIGAND M. Robots almost conquering walking， reading， dancing[EB/OL].[2018-05-09].http：//www.koreaittimes.com/story/4668/robots-almost-conqueringwalking-reading-dancing.

工控網.智能机器人的定义及分类[EB/OL].[2018-06-20]. http：//www.gongkong.com/article/201609/70782.html.

叶春明，耿文龙，陆静.基于主成分分析的我国区域专利评价研究[J].科技管理研究，2010，30（19）：128-132.

赵 宁 哈尔滨工业大学图书馆副研究馆员。 黑龙江哈尔滨，150001。

赵 翀 哈尔滨工业大学图书馆馆员。 黑龙江哈尔滨，150001。

翟凤勇 哈尔滨工业大学管理学院副教授。 黑龙江哈尔滨，150001。

刘 伟 哈尔滨联通公司助理工程师。 黑龙江哈尔滨，150001。

郭 伟 哈尔滨工业大学机器人研究所教授。 黑龙江哈尔滨，150001。

（收稿日期：2019-01-14 编校：刘 明，左静远）