2017年中国内地电影复杂网络建模与分析
刘亚云 艾均 苏湛

摘 要:复杂网络理论可用于分析各领域的复杂系统。针对中国内地电影的复杂关系,设计网络建模算法,依据2017年票房榜排名前200的电影信息,以数据集中的实体为节点、实体之间的关系为边,构建复杂网络模型,基于该模型对2017年度中国内地电影复杂网络进行分析。结果表明,高产演员对票房无明显影响;介数中心性和特征向量中心性均小于特定值時,电影票房失败的概率较高;介数中心性和特征向量中心性分布在特定区域之内时,电影获得高票房的概率高达73%。建模实验与基于模型的分析证明了2017年中国内地电影复杂网络建模的有效性,揭示了电影票房和电影复杂网络中节点中心性之间的相关性。
关键词:复杂网络;电影票房;度值中心性;介数中心性;特征向量中心性
DOI:10. 11907/rjdk. 191629 开放科学(资源服务)标识码(OSID):
中图分类号:TP303文献标识码:A 文章编号:1672-7800(2020)002-0027-08
英标:Complex Network Modeling and Analysis of Chinese Mainland Films in 2017
英作:LIU Ya-yun, AI Jun, SU Zhan
英单:(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology, Shanghai 200093,China)
Abstract: Complex network theory can be used to analyze complex systems in various fields. Aiming at the complex relationship between Chinese mainland movies, the network modeling algorithm was designed. Based on the top 200 movies in the 2017 box office list, the complex network model was constructed by taking the entities in the data set as nodes and the relationship between entities as edges. Based on this model, the 2017 complex network of Chinese mainland films was analyzed. The analysis found that productive actors have no significant influence on the box office; when the betweenness centrality and the eigenvector centrality are less than a certain value, the probability of a failure box office is higher; when the betweenness centrality and the eigenvector centrality are distributed within a specific area, the probability of a movie getting a high box office is as high as 73%. Experiments and analysis proved the effectiveness of the complex network modeling of Chinese movie in 2017, revealing the correlation between the centrality of the box office and the complex network of movies.
Key Words: complex networks; box office; degree centrality; betweenness centrality; eigenvector centrality
0 引言
现实生活中,许多复杂系统都可以建模成各种复杂网络进行分析。通常而言,复杂网络由许多个节点和连接两节点的连边组成,节点代表现实生活中的个体,而连边则用来表示个体之间的关系。有边相连的两个节点在网络中被看作是相邻的。例如,神经系统可以看作是大量神经细胞通过神经纤维相互连接形成的网络[1];计算机网络可以看作是自主工作的计算机通过通信介质如光缆、双绞线、同轴电缆等相互连接形成的网[2]。 类似的还有电力网络、社会关系网络、交通网络等[3-5]。
数学家和物理学家在考虑网络时,往往只关心节点之间有没有边相连,至于节点位置、边的长短与曲直、是否相交等特性都不在考虑范围内。网络不依赖于节点的具体位置和边的具体形态就能表现出来的性质为网络拓扑性质,相应结构为网络拓扑结构。能描述真实世界的拓扑结构系统研究,大致经历了3个阶段:第一阶段,人们认为真实系统各因素之间的关系可以用一些规则结构表示,例如二维平面上的欧几里德格网、最近邻环网;第二阶段,提出了一种新的网络构造方法,在这种方法下,两个节点之间连边与否不再是确定的事情,而是根据一个概率决定,这样生成的网络为随机网络,随机网络在很长一段时期里被认为是描述真实系统最适宜的网络[6-8];直到最近几年,由于计算机数据处理和运算能力的飞速发展,人们发现大量真实网络既不是规则网络,也不是随机网络,而是与前两者皆不同的具有统计特征的网络,这样的网络被称为复杂网络(Complex Network)[9-10]。1998年,Watts & Strogatz[1]提出小世界网络概念;1999 年, Barabá & Albert[11] 发现无标度网络特性,突破了单纯规则网络和随机网络模型的束缚,揭示了复杂网络结构所包含的各类动力学特性与结构特征之间的联系,奠定了在实际网络中应用研究的基础[12]。
当前,复杂网络用于研究各种类型的网络和网络特征,成为一大研究热点。它与现实中各类复杂性系统研究有密切关系,比如,由一些个体和个体之间互相连接而组成的社会关系网络系统、由很多神经细胞通过神经纤维互相连接组成的神经网络系统[13],以及电力网络系统、交通网络系统、生态系统网络系统和新陈代谢网络系统[13-14]等。陈培文等[15]将复杂网络与公共交通系统相结合,系统性分析了北京地铁早高峰客流现状,针对地铁网络运营提出了建议;张正帅等[16]从复杂网络的角度描述地震活动时空复杂性特征,为分析研究地震发生规律提供了一种新的途径;傅杰等[17]又从复杂网络理论角度出发,提出了一种基于网络凝聚度的电力网络关键线路评价方法。复杂网络是对现实生活中事物间关系的抽象表示,对复杂网络的研究可以帮助人们发掘事物间的深层联系,并针对特定问题提出新的解决方案。
电影是集艺术、经济和科学于一体的市场产物,近年来随着民众文化消费需求的提升以及影院和银幕数量的高速增长,我国电影行业呈现持续繁荣景象[18]。中国电影产业经历了突飞猛进的发展,并保持稳定增长的良好态势,但也出现了一些不容忽视的问题,比如:高产演员参演的影片是否一定会大卖,在社交网络中占据重要地位的制作机构参与制作的电影是否一定会取得高票房。目前,各界人士已经从传播学、经济学等角度分析电影票房影响因素,并从不同角度得出与电影票房相关的一系列理论。文献[19]通过对中国大陆地区2012-2016年期间上映电影数据进行相关性分析和回归分析,对中国大陆地区电影票房影响因素进行实证研究;文献[20]通过建立票房与明星效应之间的回归模型,对明星效应与中国电影票房进行了实证研究;文献[21]结合反馈神经网络与中国内地电影市场的实际情况,提出一种基于多层反馈神经网络的票房预测模型。
复杂网络是当前一大研究热点,但是将其应用于电影方面却鲜有涉及。本文基于复杂网络知识,针对中国内地电影的复杂关系,通过复杂网络与电影相结合,将复杂网络的研究理论系统化,设计网络建模算法。依据2017年票房榜排名前200的电影信息,以数据集中的实体为节点、实体之间的关系为边,构建复杂网络模型,并基于该模型对2017年度中国内地电影复杂网络进行系统研究分析,主要探究以下几个问题:高产演员参演的电影是否一定会大卖?高票房电影在复杂网络中有什么特征?高影响力的制作机构是否一定会带来高票房?通过建模实验与基于模型的分析,揭示电影票房和电影复杂网络中节点中心性之间的相关性,拓宽电影票房研究的新视角。
1 2017年中国内地电影复杂网络建模
1.1 复杂网络建模算法设计与实现
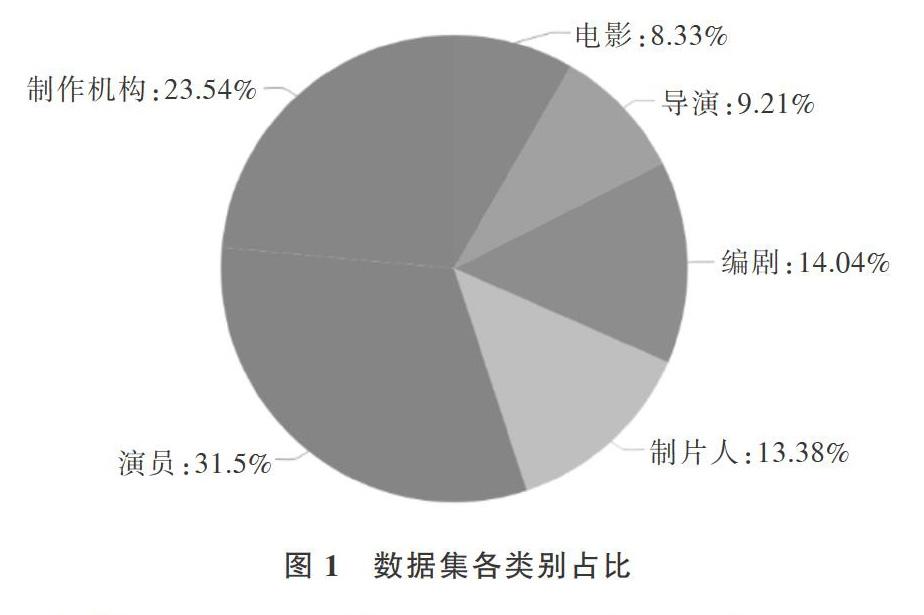
本文数据来源于国内主要电影媒体网站,如艺恩电影智库、时光网等。研究样本为2017年中国内地电影票房排行榜前220的电影,涉及电影名称、票房、上映时间、导演、编剧、制片人 、演员及制作机构。首先对数据进行预处理,删除不符合数据要求及信息不完整的20部电影,剩余200部。有导演221个,编剧337个,制片人321个,演员756个,制作机构565个,各类别统计数据占比如图1所示。
将数据关系抽象处理成复杂网络图,进行可视化分析,具体数据转化算法如图2所示。该算法主要提取两列数据:电影名称、参与电影制作的演职人员及制作机构。根据提取的数据,绘制复杂网络图。复杂网络图由节点和边构成。节点数据包括节点值和权重,边数据包括出度、入度及权重。在本文研究中,用无权无向图,不对节点进行属性区分。原来的数据集中,只能通过表格信息了解电影基本信息,例如票房、演职人员与相关制作机构等,无法探究电影票房、演职人员与制作机构等之间的关系。但是,将电影相关的数据关系抽象为复杂网络图,更便于分析票房与电影、制作机构以及演职人员之间的深层关系。
1.2 建模规则
本文对2017年中国内地电影信息进行搜集整理,包括电影名称、票房、上映时间、导演、编剧、制作人及制作机构。根据如下规则,建立复杂网络模型。
规则一:演员是参演电影的直接主体,与电影票房有着直接联系。按照演员与电影之间的联系,如果演员参演电影,便认为有关系,分别以电影和演员为节点、电影与演员之间的关系为边,建立电影—演员复杂网络。
规则二:以导演、编剧、制片人、演员和制作机构为节点,只要人物与人物、人物与制作机构、制作机构与制作机构参与同一部电影制作,便认为有关系,并建立连边,建立导演—编剧—制片人—演员—制作机构复杂网络。
规则三:电影票房规律不仅与参演演员有关,还与导演、编剧、制片人、制作机构有着密切联系。这些元素以电影为中介产生联系,分别以电影、导演、编剧、制片人、演员、制作机构为节点,电影与人物、电影与制作机构之间的关系为边,建立以電影为中心节点的电影—导演—编剧—制片人—演员—制作机构复杂网络。
通过以上3种规则分别建立了3种复杂网络,进一步探究哪种形式更适合对2017年中国内地电影票房规律进行分析。电影与演员构成的复杂网络如图3所示(其中,深蓝色节点为电影节点,粉红色节点为人物节点),不同大小表示不同度值;导演、编剧、制片人、演员以及制作机构构成的无电影复杂网络如图4所示(其中,粉红色节点为人物节点,浅蓝色节点为制作机构节点,不同大小表示不同度值);电影、导演、编剧、制片人、演员以及制作机构构成的有电影复杂网络如图5所示(其中,深蓝色节点为电影节点,粉红色节点为人物节点,浅蓝色节点为制作机构节点,不同大小表示不同度值)。算法生成之后的3种复杂网络的具体结构属性如表1所示,其中,规则一是以电影、演员为节点,彼此之间联系为边建立的复杂网络;规则二是以导演、编剧、制片人、演员,制作机构为节点,彼此之间联系为边建立的复杂网络;规则三是以电影、导演、编剧、制片人、演员,制作机构为节点,彼此之间联系为边建立的复杂网络。通过算法生成网络时,如果同一演职人员具有多重身份,按一个节点进行处理。由表1可以看出,按照不同规则建立的复杂网络结构属性差异较大。按照规则一建立的复杂网络,节点数仅为957个,社团个数却有90个,社团规模较小,整个复杂网络的节点分布比较分散。各节点间的平均路径也比较长,相连两个节点平均需要12.86步。按照规则二建立的复杂网络,节点数为2 023个,节点之间的连边有13 998条,在此规则下建立的复杂网络无电影节点,只要人物与制作机构参与同一部电影制作,便认为有关系,这样通过电影有间接联系的人物与制作机构节点间便有了直接联系,强化了节点间的连接,造成复杂网络中节点度过大、不同类型节点之间的连边存在大量冗余,使得节点间的区分度降低。按照规则三加入电影节点,建立的复杂网络也是规则二中5类节点与电影之间的不同二部图关系投影所得,其中,节点数为2 223,节点间连边为2 429条,模块度为0.895,社团结构特性相较于规则二更为明显。
1.3 2017年中国内地电影复杂网络模型构建
分析发现,不同规则建立的复杂网络结构属性差异较大。规则一所建复杂网络模型节点少、社团规模较小、节点分布较分散,且只将电影票房与演员联系在一起,忽略了其它因素影响;规则二所建复杂网络模型,连边之间存在大量冗余,整个网络平均度值较大;规则三的社团结构特性相较于规则二更为明显,并且加入电影节点构建复杂网络,在分析电影票房规律时更为直观。因此,本文最后选择规则三建立包含电影节点的电影—导演—编剧—制片人—演员—制作机构复杂网络。在该网络中,将导演、编剧、制作人、演员和制作机构统一抽象为一类节点,没有进一步对其属性进行区分。如果演员出演电影,演职人员和制作机构参与电影制作,就被认为与电影有关。以电影、演职人员以及制作机构为节点,各节点间的关系连接为边建立无向复杂网络,即2017年中国内地电影复杂网络。
2 2017年中国内地电影复杂网络分析
2.1 节点中心性分析指标
本文研究的复杂网络均为无权无向网络,拟采用社会网络分析法评价节点重要性。社会网络分析方法起始于20世纪40年代末,常用于评价节点重要性。该方法主要基于这样一种假设:“重要性等于显著性”,即节点重要性等价于该节点与其它节点的连接而使其具有显著性[22]。复杂网络采用了图论与社会网络分析[23]中的许多统计指标,用于度量网络拓扑结构的复杂网络特征,包括节点的度值中心性(Degree Centrality)[24]、介数中心性(Betweenness Centrality)[25]、特征向量中心性(Eigenvector Centrality)[26]等。为研究2017年中国内地电影票房的复杂网络特性,本文对上述指标进行了计算分析。
2.1.1 度值中心性
度值中心性(Degree Centrality)是指节点的度值越大则节点越重要,通常用[Ki]表示节点的度值,该判据是评估节点重要度最简单的方法。度值中心性是网络节点重要度的静态刻画,由于网络尺寸N不同,通常采用归一化度值中心性评估节点重要度。
度中心性是典型的局部信息判据,不能从网络全局信息层次分析节点重要程度。
2.1.2 介数中心性
介数中心性(Betweenness Centrality)基于网络全局信息,考察所有节点对之间最短路径的数目,节点对之间的最短路径通常存在多条,若节点位于最短路径上的次数越多,则该节点越重要。如果njk是连接节点j和k之间最短路径数目,njk(i)是连接节点j和k之间包含着节点i的最短路径数目,则节点i的介数中心性定义为:
介数中心性相当于一个节点担任最短路径桥梁的次数和所有路径数量的比值。因此,当一个节点出现在其它两个节点间最短路径上的次数越多,该节点的介数中心值越大。
2.1.3 特征向量中心性
特征向量中心性(Eigenvector Centrality)。一个节点特征向量中心性值由其邻居节点的值决定,即一个节点的中心化指标应该等于其相邻节点的中心化指标之线性叠加。节点i的特征向量中心性定义为:
特征向量中心性反映一个节点的重要性不仅与其邻居节点的度值有关,也与其邻居节点的重要性有关。
2.2 节点中心性分析
2.2.1 节点度值中心性分析
在该无向复杂网络中,网络节点的度值是指与之相连接的所有边的总和,电影节点的度值就是指电影与演职人员、制作机构所有连接边的总和。在一个复杂网络中,度值中心性认为一个节点的相邻节点数目越多,影响力就越大,这是网络中刻画节点重要性的最简单指标。在此网络中,电影的度值大小反映了参与电影制作人力资源的多少,即电影节点的度值越大,表示有越多的人和越多的制作机构参与电影制作。
通过分析统计,电影票房复杂网络中节点的平均度为2.185,说明在此复杂网络中平均每个节点影响2.185个其它节点。图6(a)是度值分布散点图,可以发现复杂网络中度值的分布遵守幂律分布。从度值占比饼状图6(b)中可以看出,此网络中度值为1的节点占据整个网络的79.16%,在剩下節点中占比较重的也是度值为2的节点,即这些与其它联系很少的节点占据了网络中相当大的比重。较高度值节点占少数,而这些度值较高的节点具有较强的关联性,主要分布在网络结构中心。度值的分布散点图与度值占比饼状图,印证了电影票房复杂网络的无标度性,即在网络中的大部分节点只和很少节点连接,而有极少节点与非常多的节点连接。
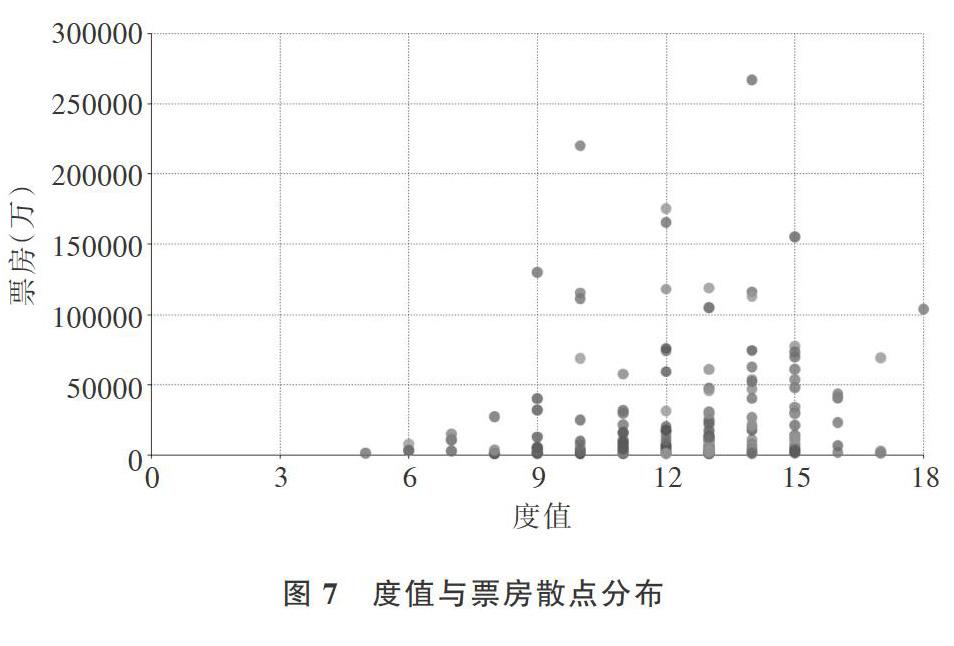
图7是度值与票房分布散点图,可以看出度值在9~18之间出现票房超过10亿的电影。但是,在该范围内,高度值、低票房的电影占到了大多数,说明高投资不一定能换得高票房。影响票房因素很多,因此,在电影投资过程中不能盲目投入,要量化分析,理性投资。
对本文复杂网络分析发现,任达华、成龙、岳云鹏节点度值最高,即2017年出演电影数量最多。但从图8高度值演员参演电影排名折线图(电影排名越小票房越高)发现,2017年参演电影较多的演员中,除成龙外,其他几位演员所参演的电影只有极少数有着高票房,说明高产演员不一定能带来高票房。由此,根据度值大小计算方式可知,电影度值大小取决于与电影相关的人物和制作机构的数量,并不能真实表现出电影票房网络的中心性。因此,度中心性虽然计算方便简单,但不能很直观地反映中国内地票房复杂网络的中心性。
2.2.2 介数中心性分析
电影是演职人员和电影制作机构合作的桥梁,复杂网络中电影节点介数中心性越高,表明该电影越有影响力。与此同时,在复杂网络拓扑图中删除该电影节点对其它节点影响更大。同理,演职人员节点、制作机构节点的介数中心性越大,说明他们的影响力越大。
根据介数中心性对节点进行排序,表3是依据介数中心性统计的主要人员及其参演电影排名;图9是电影介数中心值与票房的散点分布图;图10是介数中心性排名前50和后50的电影票房折线图。
参考文献:
[1] WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world networks[J]. Nature,1998,393(6684):440-442.
[2] FALOUTSOS M,FALOUTSOS P,FALOUTSOS C. On power-law relationships of the Internet topology[J]. Poceedings of ACM SIGCOMM,1999,29(4):251-262.
[3] LILJEROS F, EDLING C R, AMARAL L A N, et al. The web of human sexual contacts[J]. Nature,2001, 411(6840): 907.
[4] EBEL H, MIELSCH L I, BORNHOLDT S. Scale-free topology of e-mail networks[J]. Physical review E, 2002, 66(3): 035103.
[5] SEN P,DASGUPTA S,CHATTERJEE A,et al. Small-world properties of the Indian railway network[J]. Physical Review E,2003,67(3): 036106.
[6] ERDOS P, RéNYI A. On the evolution of random graphs[J]. Transactions of the American Mathematical Society,1960, 5(1): 17-60.
[7] ERD?S P, RéNYI A. On the strength of connectedness of a random graph[J]. Acta Mathematica Hungarica, 1961, 12(1-2): 261-267.
[8] BOLLOBáS B, SIMON I. Repeated random insertion into a priority queue[J]. Journal of Algorithms,1985,6(4): 466-477.
[9] TRAVERS J, MILGRAM S. The small world problem[J]. Phychology Today, 1967, 1(1): 61-67.
[10] 周涛,柏文洁,汪秉宏,等. 复杂网络研究概述[J]. 物理, 2005, 34(1):31-36.
[11] BARABASI A L, ALBERT R. Emergence of Scaling in Random Networks[J]. Science, 1999, 286(5439):509-512.
[12] 蔡泽祥,王星华,任晓娜. 复杂网络理论及其在电力系统中的应用研究综述[J]. 电網技术,2012, 36(11):114-121.
[13] WANG X F,CHEN G. Complex networks: small-world, scale-free, and beyond[J]. IEEE Circuits and Systems Magazine, 2003, 3(1):6-20.
[14] JEONG H,TOMBOR B,ALBERT R,et al. The large-scale organization of metabolic networks[J]. Nature,2000,407(6804):651-654.
[15] 陈培文,陈峰,胡映月,等. 基于复杂网络的城市轨道交通网络中心性研究[J]. 复杂系统与复杂性科学, 2017(2):97-102.
[16] 张正帅,陈时军,周晨,等. 利用复杂网络技术分析地震活动性特征[J]. 复杂系统与复杂性科学, 2018(2):10-17.
[17] 傅杰,邹艳丽,谢蓉. 基于复杂网络理论的电力网络关键线路识别[J]. 复杂系统与复杂性科学, 2017(3):95-100.
[18] 韩忠明,原碧鸿,陈炎,等. 一个有效的基于GBRT的早期电影票房预测模型[J]. 计算机应用研究, 2018(2):410-416.
[19] 何双男. 中国大陆地区电影票房影响因素实证研究[J]. 电影文学, 2017(22):4-8.
[20] 郭新茹,黄舒沁. 明星效应与中国电影票房的实证研究[J]. 现代传播:中国传媒大学学报, 2017(12):120-125.
[21] 郑坚,周尚波. 基于神经网络的电影票房预测建模[J]. 计算机应用, 2014, 34(3):742-748.
[22] 赫南,李德毅,淦文燕,等. 复杂网络中重要性节点发掘综述[J]. 计算机科学, 2007,34(12):1-5.
[23] 罗家德. 社会网分析讲义[M]. 北京:社会科学文献出版社, 2010.
[24] FREEMAN L C,ROEDER D,MULHOLLAND R R. Centrality in social networks: II. experimental results [J]. Social Networks,1979,2(2):119-141.
[25] LIU Y Y, SLOTINE J J, BARABáSI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346):167.
[26] EVERETT M, BORGATTI S P. Ego network betweenness[J]. Social Networks,2005,27(1):31-38.
[27] 汪宏,鲍中奎,张海峰. 基于标签传播识别网络中的关键节点[J]. 复杂系统与复杂性科学, 2017(2):19-25.
(责任编辑:孙 娟)

