基于波束域LC-GSC的降秩波束形成算法
陈伟 秦云


摘 要:針对传统GSC算法在处理大型阵列天线时,所需运算量大、工程上难以应用等问题,提出一种基于波束域LC-GSC的降秩波束形成算法。与传统GSC算法相比,它能够在期望信号和特定干扰方向上形成约束响应,利用构造的转换矩阵将信号变换到波束域,并能够降低计算量,加快自适应收敛速度。根据信号特征值大于噪声特征值,可以得到波束域协方差矩阵逆的高次幂基本等价于信号子空间,信号子空间的求取也方便构造阻塞矩阵。降秩矩阵可以利用GSC下支路的快拍数构造,进一步降低运算量。最终根据算法得到自适应权矢量,为了使系统有更好的信噪比稳健性,可以将权矢量向信号子空间投影。通过对GSC算法进行分析并改进,给出算法在FPGA上的实现方案。实验仿真表明,该算法能够在期望信号方向准确形成主瓣,干扰方向准确形成零陷且副瓣电平降低5~10dB。基于波束域LC-GSC的降秩波束形成算法有很好的波束形成性能,算法稳健性较好。
关键词:LC-GSC;波束域;自适应波束形成;信号子空间;降秩矩阵;阻塞矩阵
DOI:10. 11907/rjdk. 191552 开放科学(资源服务)标识码(OSID):
中图分类号:TP312文献标识码:A 文章编号:1672-7800(2020)002-0012-06
英标:A Reduced Rank Beamforming Algorithm Based on Beam Domain LC-GSC
英作:CHEN Wei,QIN Yun
英单:(School of Electrical and Information Engineering, Jiangsu University,Zhenjiang 212000,China)
Abstract: When the traditional GSC algorithm is used to process large array antennas, it requires a large amount of computation and is difficult to apply in engineering. In this paper, a beam-domain LC-GSC-based reduced rank beamforming algorithm is proposed. Compared with the traditional GSC algorithm, it can form a constrained response in the desired signal and the specific interference direction, transform the connected signal into the converted matrix, and reduce the amount of calculation. The speed of the adaptive convergence can be accelerated. Then, according to the signal eigenvalue greater than the noise eigenvalue, the inverse power of the beam domain covariance matrix can be obtained, which is substantially equivalent to the signal subspace. The calculation of the signal subspace also facilitates the construction of the blocking matrix. The rank reduction matrix can be constructed by using the snapshot number of the branch under the GSC, which further reduces the amount of calculation. Finally, the adaptive weight vector is obtained according to the algorithm. In order to make the system have better signal-to-noise ratio robustness, the weight vector can be projected to the signal subspace. Through the analysis and improvement of the GSC algorithm, the implementation scheme of the algorithm on the FPGA is given. Experimental simulations show that the proposed algorithm can accurately form the main lobe in the desired signal direction, the interference direction accurately forms a null trap and the sidelobe level also has a 5~10 dB reduction. The beam-slope LC-GSC-based reduced rank beamforming algorithm has good beamforming performance and good algorithm robustness.
Key Words: LC-GSC;beam-domain;adaptive beamforming;signal subspace;reduced rank matrix;blocking matrix
0 引言
阵列信号处理[1]在信号处理领域占有很大比重,在导航、雷达、医学声呐、地质勘测、无线电通讯和声呐中都有较好应用。波束形成[2]作为阵列信号处理的重要研究方向,其实质是空域滤波,通过对阵列输出信号给定不同的权值,能够实现信号空域滤波的目的,其加权值决定了空间滤波的特性。根据不同的加权值,波束形成又分为常规波束形成[3]和自适应波束形成[4]。前者权值固定,方向图难以变化控制,抗干扰能力差。自适应波束形成权值能够随着信号环境自适应变化,以使方向图主瓣对准期望信号,干扰方向形成零陷从而抑制干扰,阵列输出的信干噪比(SINR)达到最大。
自适应阵列处理分为直接形式自适应阵列处理和GSC框架自适应阵列处理两大类,后者是目前阵列天线自适应波束形成技术的热点研究方向。对于阵元数较多的大型天线阵列,GSC降秩自适应波束形成算法能够减小算法所需计算量,提高收敛速度。目前,自适应波束形成在阵元域研究较多,而在波束域研究相对较少。文献[5]首次提出了用部分自适应自由度对波束形成进行降维处理;文献[6]提出了波束域MVDR算法;文献[7]提出了波束域LCMV算法,算法运算量得到有效降低;文献[8]讨论了算法在阵元域与波束域的不同:一个是在全部阵元使用不同的加权矢量,另一个是在不同子阵使用相同的加权矢量。波束域自适应波束形成算法降低了系统的计算复杂度而没有自由度损失,使得自适应处理容易实现且具有较好的鲁棒性。目前,波束域算法有波束域对角加载算法[9]、前向和后向空间平滑算法[10-11]以及波束域特征空间法[12]等。傳统的降秩变换GSC波束形成需要对协方差矩阵进行特征分解得到降秩矩阵,如文献[13]中信号子空间提出的主分量法(PC),文献[14]根据SINR最大提出的交叉谱法(CSM),并且特征分解需要较高的计算量,不利于工程实现。文献[15]简化了降秩矩阵的结构,在输出均方误差最小原则下利用迭代方法求降秩矩阵及最优权系数,但是该方法受预先设置的降秩矩阵集的影响。
针对上述问题,本文提出一种波束域LC-GSC降秩自适应波束形成算法,与文献[16]的不同之处在于它引入了线性约束,不仅保证了期望信号无失真,还可以在特定方向上对干扰进行约束并产生零陷。特征空间不是通过特征分解求得,而是通过波束域协方差矩阵逆的高阶次幂近似等价于信号子空间投影矩阵。相对于特征分解,该方法能够有效减小计算量,同时求得的投影矩阵也方便了下支路阻塞矩阵和降秩矩阵构造。借鉴Hung—Turner快速投影(HTP)算法[17-20]中快速估计干扰子空间的思想,结合GSC框架优点,利用GSC下分支的中间快拍数据构造降秩矩阵。在此基础上,提出了快速干扰估计干扰空间的方法,通过使用所有可用的快拍数(多于干扰个数)构造降秩矩阵,并且最后将求得的自适应权矢量投影到信号子空间,该方法有效减轻了期望信号相消现象,提高了算法的鲁棒性,从而得到了文中提出的改进算法。本文提出的一种波束域LC-GSC降秩自适应波束形成算法具有很好的鲁棒性、收敛性、实时性,输出信号的SINR也较高,且计算复杂度得到了有效降低,算法在工程上更利于实现。仿真结果表明,该算法有良好的波束形成性能,验证了算法的有效性。
1 阵列模型
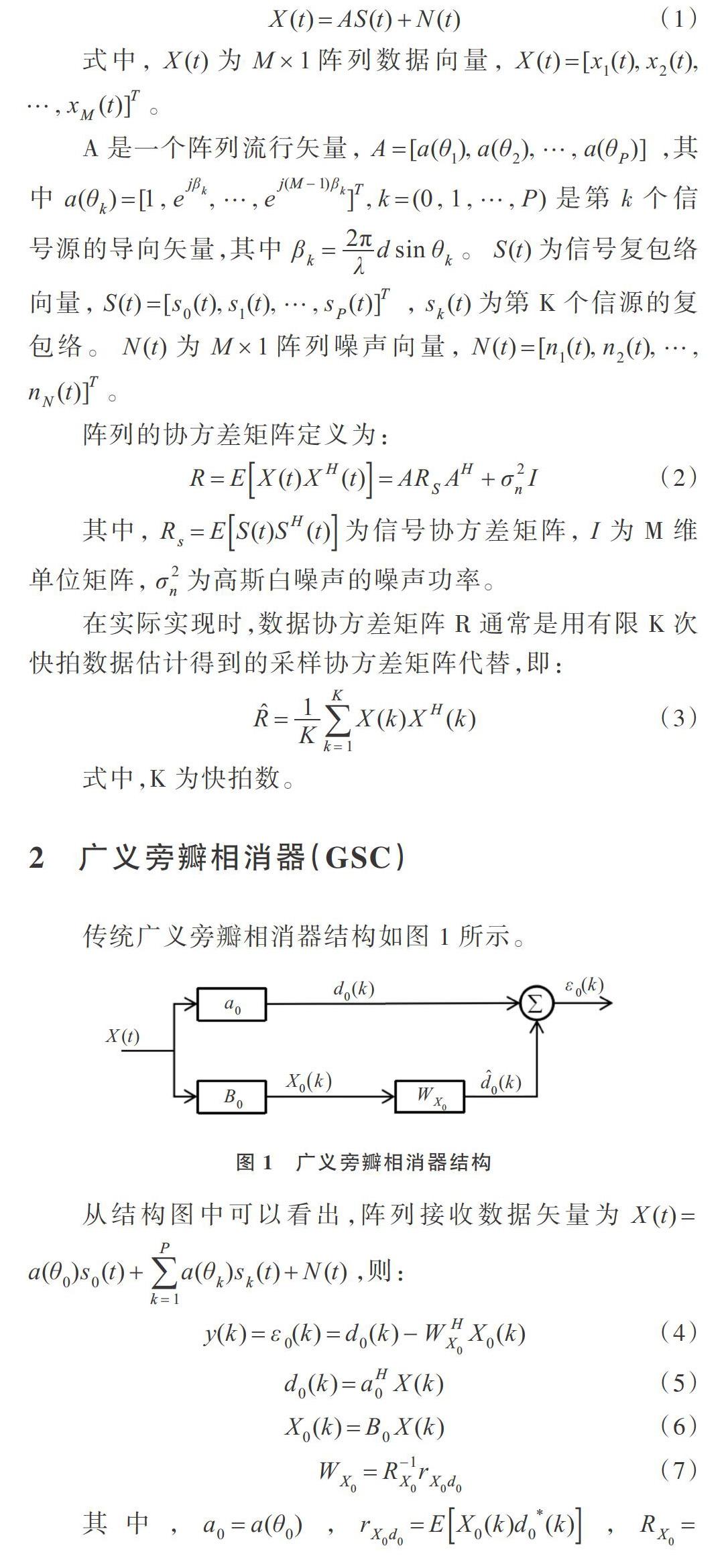
假设有一个带有M个全方向性阵元的理想均匀线性阵列接收P+1( 式中,[X(t)]为[M×1]阵列数据向量, A是一个阵列流行矢量,[A=[a(θ1),a(θ2),?,a(θP)]] ,其中[a(θk)=[1,ejβk,?,ej(M-1)βk]T,k=(0,1,?,P)]是第k个信号源的导向矢量,其中[βk=2πλdsinθk]。[S(t)]为信号复包络向量,[S(t)=[s0(t),s1(t),?,sP(t)]T] ,[sk(t)]为第K个信源的复包络。[N(t)]为[M×1]阵列噪声向量,[N(t)=[n1(t),n2(t),?,][nN(t)]T]。 阵列的协方差矩阵定义为: 其中,[Rs=ES(t)SH(t)]为信号协方差矩阵,[I]为M维单位矩阵,[σ2n]为高斯白噪声的噪声功率。 在实际实现时,数据协方差矩阵R通常是用有限K次快拍数据估计得到的采样协方差矩阵代替,即: 式中,K为快拍数。 2 广义旁瓣相消器(GSC) 传统广义旁瓣相消器结构如图1所示。 从结构图中可以看出,阵列接收数据矢量为[X(t)=][a(θ0)s0(t)+k=1Pa(θk)sk(t)+N(t)],则: 其中,[a0=a(θ0)],[rX0d0=EX0(k)d0*(k)],[RX0=][EX0(k)X0H(k)=B0RXB0H],[WX0]为匹配滤波器。[(M-1)×][M]行满秩阻塞矩阵[B0]需满足: 广义旁瓣相消器的主要思想:使用已知的期望信号方向信息将阵列接收信号变换为上下两个支路。其中,上支路(主支路)经期望信号的空间匹配滤波后得到参考信号[d0(k)],[d0(k)]含有期望和干扰信号,且变换后期望信号满足无失真约束响应。而下支路则通过[(M-1)×M]行满秩阻塞矩阵[B0]阻塞期望信号,则下支路中[(M-1)×1]数据矢量[X0(k)]只含干扰。显然上支路和下支路中的干扰是相关的,对变换后的信号采用维纳滤波,则可以自适应消除上下支路中的干扰,最终上支路中的期望信号无失真地输出。因此,广义旁瓣相消器中的上下支路输出误差就是阵列输出。 GSC的等效权矢量可写为: 3 基于波束域LC-GSC的降秩算法 针对传统GSC算法运算复杂度高、系统稳健性差、收敛较慢等特点,本文提出基于波束域LC-GSC框架的降秩波束形成算法,该算法结构如图2所示。 线性约束最小方差(LCMV)波束形成器是最小方差无失真响应(MVDR)波束形成器的进一步推广,而广义旁瓣相消器(GSC)相当于MVDR算法,对GSC作进一步推广,可得到LCMV的广义旁瓣相消结构—线性约束广义旁瓣相消器(LC-GSC)。用构造的波束转换矩阵T将其转换到波束域,就可以得到本文提出的算法。 自适应波束形成算法最重要的是得到自适应权值,为了求波束域权矢量,要求得到波束域的信号协方差矩阵和波束域的阵列流形矢量。先用转换矩阵T将阵元域信号变换到波束域,即: 式中,T是[M×L] 维矩阵,L是形成波束数目,可以在感兴趣的空间形成L(L 线性约束最小方差(LCMV)波束形成器可以表示为: 其中,C是约束矩阵,f是相应的约束响应矢量。一般地: 由此可以得到LCMV权矢量的直接形式: 线性约束广义旁瓣相消器的主支路静态权矢量为[Wq=C(CHC)-1f],则波束域主支路的流形矢量变为[α(θ)=][THWq]。通过转换矩阵T将输入信号和阵列流形矢量变换到波束域之后,传统用期望信号导向矢量[a(θ)]构造匹配滤波器的方法不再适用,这里可以用波束域流形矢量[α(θ)]构造。 下支路阻塞矩阵[B0]也不再适用传统方法构造,需要构造新的波束域阻塞矩阵。 由于阻塞矩阵[B0]要满足约束条件[B0a(θ0)=0],可以取[a(θ0)]的正交补空间的一个基,其维数为[(M-1)×M]。具体构造方法如下: 显然,阻塞矩阵[B⊥h0_p=0]。 主分量法(PC-GSC)、交叉谱法(CS-GSC)、降秩共轭梯度法(RR-CG)以及降秩多级维纳滤波器(RR-MWF)等都是GSC框架中构造降秩矩阵的常用方法。 本文采用一种简便方法快速构造降秩矩阵,GSC框架中下支路[X(t)]转换到[XT(t)],再由阻塞矩阵变到[XB(k)],由于[B⊥C=0],因此[XB(k)]中仅有干扰信号和噪声。 其中,[k=1,2,?,P]为干扰信号,[N(t)]为背景噪声。 设P个快拍数据组成的矩阵为[XB=XBt1,XBt2,?,XBtP] 。由上式可知,当[XB(k)]只含干扰信号时,[XB(k)]的列向量与[A=a(θ1),a(θ2),?,a(θP)]的列向量形成相同空间,即: 当干扰噪声所占比重较大时,[XB(k)]的列向量与A的列向量形成的空间大致相同。通常,干扰数量未知,q是估计的干扰数量。本文可以利用所有可得到的K个波束域快拍数据估计降秩矩阵。取[Tj1=XB=[XBt1,XBt2,?,][XBtq]],[Tj2=XB=XBt2,XBt3,?,XBtq+1],[Tj(K-q+1)=][XB=XBtK-q+1,][XBtK-q+2,?,XBtK],然后取平均: 上式主要是加法运算,运算量比传统方法小很多,且算法稳健性较好。 传统方法构造降秩矩阵需要[οM-13]的运算量,而本文快速算法只需要[K-q+1q]次复数加法和一次复数乘法。相较于传统算法,其运算量得到有效降低,便于工程应用实现。 通常,为了提高算法稳定性,可以用特征空间法将求得波束域的自适应权值向信号子空间投影,校正求得的权值,这样得到的波束域自适应权值具有一定的稳健性。求信号子空间需要对信号自相关矩阵进行特征分解,它会产生复杂计算。本文运用一种波束域简化的特征空间算法,利用波束域协方差矩阵矩阵逆的高阶次幂去表达信号子空间,因而无需对自相关矩阵特征进行分解,算法运算量进一步降低。在对这种方法的推导过程中,对波束域协方差矩阵特征分解如下: 其中,[λ1>λ2>?>λP+1>λP+2=?=λM],特征值按从大到小排列,P+1个较大特征值对应的特征向量形成相应的信号和干扰子空间。 剩下M-P-1个特征值,其对应的特征向量形成噪声子空间。 对上式变形得到: 其中,[ΛS=diagλ1σn2,λ2σn2,?,λP+1σn2] ,因为[λiσn2>1,i=][1,2,?,P+1],当参数[c→∞]时,式子的第一项就为零,则上式求逆就可以变为: 在理想状况下,信号子空间[ES]与噪声子空间[EN]正交,噪声子空间的补可以表示信号子空间的投影矩阵。 综上,基于波束域LC-GSC降秩自适应波束形成算法的权值为: 式中,T是波束域变换矩阵,[ESESH]是[L×L]维波束域信号子空间投影矩阵,[B⊥]是[(L-1)×L]维波束域阻塞矩阵,[aBθ0]是目标信号波束域阵列流形矢量,[Tj]是[(L-1)×q]維降秩矩阵。[WB]是自适应权值,其值为: 由上式可以看出,只需对[q×q]维的矩阵[TjHB⊥RTB⊥HTj]执行求逆运算,而不必对[L×L]维的协方差矩阵[RT]或者[M×M]维的协方差矩阵[R]求逆,因而降低了运算量。整个算法流程中并没有涉及特征分解,且提高了阻塞矩阵和降秩矩阵的性能,算法具有很好的鲁棒性、收敛性、实时性,每一步矩阵构造都能够降低算法运算复杂度,极大促进了算法在实际工程中的应用实现。 波束域LC-GSC的降秩自适应波束形成算法流程可以表示如下:①通过转换矩阵T将阵元域信号和阵列流形矢量变换到波束域;②计算变换后的波束域协方差矩阵和信号子空间;③利用波束域信号子空间构造阻塞矩阵;④利用波束域广义旁瓣相消器下支路的中间快拍数据构造降秩矩阵;⑤将波束域自适应权值投影于信号子空间。 4 基于波束域LC-GSC的降秩自适应波束形成算法的FPGA实现 由上述可知,通过波束域LC-GSC降秩自适应波束形成算法,系统运算量得到了有效降低,且具有很好的鲁棒性、收敛性、实时性。针对数字波束形成系统数据量大,对系统处理速度、实时性要求高,但运算结构相对简单等特点,适合用FPGA硬件进行多路并行处理,同时兼顾速度和灵活性。同时,算法中也存在一些控制较为复杂而计算量较小的部分,采用Nios软核实现此部分算法较好。 4.1 整体结构 如图 3所示,整个算法系统主要由Nios软核和乘法累加器模块构成。Nios软核可以处理不适合硬件运行的复杂部分,乘法累加器模块可以完成波束形成中大量的矩阵相乘。控制总线则用来负责数据流通。 4.2 乘法累加器模块 该模块用来实现FPAG中最重为要的并行矩阵乘法,例如矩阵[An×m]和m维向量x的乘法计算,[yi=j(Aij×xj)]。 如图 4所示,可以将乘法运算分为n次,每一次用m个乘法器并行运算,然后用加法器完成累加运算。 采用这种结构能够快速完成矩阵乘法运算,每个时钟出来一个数据,n个时钟周期产生一个结果向量。 4.3 Nios模块 该模块主要处理算法中不适合硬件运行的复杂部分,用以实现波束域LC-GSC降秩自适应波束形成算法,具体算法在Eclipse 环境中用C语言完成编写。算法整体流程如图 5所示,各部分算法完成矩阵累乘加运算。 5 仿真分析 为了验证算法性能,本文利用MATLAB将FPGA得到的权值矢量,在阵列方向图进行验证。仿真时,假定一个均匀线性阵列,阵元总数为20,阵元间距与波长的比值为0.5。有3个来自远场窄带互不相关的入射信号,一个期望信号和两个干扰信号,期望信号方向0°,两个干扰方向10°和30°,采样快拍数为1 024,信噪比(SNR)为0dB,干噪比(INR)为10dB。 对于均匀线性线阵,波束域转换矩阵T为: 式中,[μα=1,ejπα,ej2πα,?,ej(N-1)παT],系数k决定了波束覆盖空间的起始位置。构成矩阵T的各个列向量分别代表不同的方向,在感兴趣空间形成p个波束,这里取k=-7,p=15。 仿真1:仿真算法为本文提出的算法,与常规波束形成(CBF)算法进行比较。仿真结果如图 6所示,估计干扰个数q=2。 可以看出,波束域LC-GSC降秩算法与常规波束形成相比主瓣宽度大体差不多,但是波束域算法能在干扰方向上准确产生零陷,有效抑制干扰,提高信干噪比,而常规算法产生零陷方向有一定偏差,不能够准确抑制干扰。 仿真2:同仿真1条件相同,唯一不同的是降秩矩阵的维度不同,仿真2的估计干扰个数q=3。仿真結果如图7所示。 可以看到,同仿真1结果大抵相同,它在10°和30°方向能够形成更深的零陷。 仿真3:同仿真1条件相同,唯一不同的是降秩矩阵维度不同,仿真3的估计干扰个数q=1。仿真结果如图8所示。 可以看到,它同前面两个仿真形成的波束也大抵相同。由此可见,该实验条件下干扰估计个数与实际干扰个数相差在一定范围内对最终的波束形成并不算敏感,因此本文提出的算法具有良好的稳健性,自适应波束形成能力良好。 仿真4:同前面仿真条件相同,估计干扰个数q=2,仿真算法为本文提出的波束域LC-GSC算法,与传统阵元域GSC算法进行比较。仿真结果如图9所示。 可以看出,本文提出的波束域LC-GSC算法与传统GSC算法相比,波束域算法能够在干扰方向形成更深的零陷,干扰抑制效果较好,有效提高了信干噪比(SINR),且能够形成更低的旁瓣,性能更好。 仿真5:同前面仿真条件相同,估计干扰个数q=2,仿真算法为本文提出的波束域子空间投影LC-GSC算法,与波束域非子空间投影LC-GSC算法进行比较。仿真结果如图10所示。 可以看出,波束域子空间算法能够准确在0°形成主瓣,在10°和30°形成零陷。而传统的LC-GSC算法却在0°形成信号相消现象,且干扰形成的零陷也有一定偏移,系统信干噪比较低。 仿真6:同前面仿真条件相同,估计干扰个数q=2,对本文提出算法的功率谱进行仿真,与传统CBF算法进行比较。仿真结果如图11所示。 可以看出,本文算法较传统CBF算法分辨率大幅提高。CBF算法出现两个较宽波峰,无法准确分辨来波方向,而本文算法出现3个波峰,能够准确分辨出目标的来波方向。 6 结语 本文提出了波束域LC-GSC的降秩自适应波束形成算法,与传统算法相比,文中算法在每一步矩阵构造中都能够减少一定计算量,这样算法最后总的运算量就得到了极大降低,有利于工程应用。同时为了提高算法稳健性,将最后求得的波束域自适应权值向信号子空间投影,对权值进行校正,可以得到稳健的波束域权值。给出了算法在FPGA中的实现过程,并利用MATLAB对算法的实现结果进行了仿真验证。仿真结果表明,该算法能够有效避免期望信号相消现象,且变换到波束域后算法能够形成更深的零陷以及更低的旁瓣,提高了算法的SINR及其对信号的分辨率,该算法具有良好的波束形成能力。 参考文献: [1] 王永良. 自适应阵列处理[M]. 北京:清华大学出版社,2009. [2] JAMES W. A comparison of robust adaptive beamforming algorithms[J]. IEEE transactions on Signal Processing,2007,55(11):5323- 5336. [3] 龚耀寰. 自适应滤波一时域自适应滤波和智能天线[M]. 北京:电子工业出版社,2003. [4] GERSHMAN A B. Robust adaptive beamforming in sensor arrays[J]. International Journal of Electronic Commerce,1999,53:305-314. [5] BIENVENU G,KOPP L. Decreasing high resolution method sensitivity by conventional beamformer processing[C]. Proc. of IEEE ICASSP,1984: 714-717. [6] 曾浩,劉玲,杨士中. 基于对角负载的波束空间波束合成器[J]. 系统工程与电子技术,2007,29(7):1041-1044. [7] HU H,DENG X H.An improved LCMV method at subarray level[C]. Proc of IET International Conference on Wireless,Mobile and Multimedia Networks,2006: 1-4. [8] ZOLTOWSKI M. High resolution sensor array signal processing in the beam-space domain: novel techniques based on the poor resolution of fourier beamforming[C]. Fourth Annual ASSP Workshop on Spectrum Estimation and Modeling,1988,350-355. [9] 曾浩,周国,郑芳. 雷达阵列中前后向平滑协方差矩阵估计应用[J]. 计算机工程与应用,2009,45(18): 227-230. [10] 游鸿,黄建国,徐贵民. 基于MVDR的阵列信号波束域预处理算法[J]. 系统工程与电子技术,2008,30(1): 64-67. [11] 曾浩,刘玲,杨士中. 基于对角负载的波束空间波束合成器[J]. 系统工程与电子技术,2007,29(7):1041-1044. [12] 郭金瑞,朱德智,代月花,等. 波束域特征空间自适应波束形成算法[J]. 系统仿真学报,2011,23(1):142-145. [13] CARHOUN D O,GAMES R A,WILLIAMS R T. A principal components sidelobe cancellation algorithm[C]. TwentyFourth Asilomar Conference on Signal,Systems and Computers. Pacific Grove,1990: 763-768. [14] GOLDSTEIN J S,REED I S. Subspace selection for partially adaptive sensor array processing[J]. IEEE Transactions on Aerospace and Electronic Systems,1997,33(2):539-544. [15] ZANATTA FILHO D,DE LAMARE R C,FA R. Reduced-rank interference suppression for GPS systems based on adaptive basis-function approximation[C]. 42nd Asilomar Conference on Signals,Systems and Computers. Pacific Grove,2008: 1635 -1639. [16] 戴华骅,王亚森,赵英潇,等. 一种基于GSC框架波束域快速稳健自适应波束形成算法[J]. 科学技术与工程,2014,14(29):39-43. [17] ZATMAN M. Properties of Hung-Turner projections and their relationship to the eigencanceller[C]. Conference Record of the Thirtieth Asilomar Conference on Signals,Systems and Computers. Pacific Grove,1996: 1176-1180. [18] HUNG E K,TURNER R M. A fast beamforming algorithm for large arrays[J]. IEEE Transactions on Aerospace and Electronic Systems,1983,19(4):589-607. [19] NICKEL ULRICH R O. Fast subspace methods for radar applications[C]. Proceedings of SPIE,1997:438-448. [20] 丁前军. 降秩自适应波束形成技术研究[D]. 西安:空军工程大学,2006. (责任编辑:孙 娟)

