大跨度悬索桥地震行波效应分析

黄 康

(招商局重庆交通科研设计院有限公司， 重庆 400067)

欧洲规范[1]规定：当桥长大于200 m且存在地质不连续或明显的不同地貌，或桥梁总长大于600 m时，无论地质情况如何，均应考虑地震动的空间变化对结构的影响。我国JTG/T B02-01—2008《公路桥梁抗震设计细则》[2]第5.1.3条规定：若桥址存在地质不连续，或地形特征可能造成各桥墩的地震动参数显著不同，以及桥梁一联总长超过600 m时，宜考虑地震动的空间效应，包括波传波效应、失相干效应和不同塔墩基础的场地差异。大量地震记录表明，在同一次地震中，地表各处的反应不同，因此，大跨复杂结构应当考虑地震动多点激励的影响。多点激励与一致激励的分析结果比较也似乎难以找到规律性[3]。由于多点激励下地震动输入的复杂性，采用行波效应模拟多点激励是一种比较简单合适的方法[4]。范立础等[5]对南京长江二桥南汊桥做了非一致地震激励下响应特征研究分析后，认为水平视波速从500 m/s开始取值，考虑了行波效应的结构响应与一致激励产生的结果有40%的差异。焦常科等[6]在分析泰州长江公路大桥行波效应研究时，视波速区间选取为300 m/s～7 000 m/s，其研究显示低视波速对结构相应的影响存在一定的振荡性，但随着视波速的增大相关响应趋于稳定。 赵青等[7]结合工程实例针对斜桥的行波效应得出随着剪切波速的增大，索力的变化无明显的规律。近年来多点激励输入问题的实际工程研究较少[8]，本文以某长江大跨悬索桥为例，采用行波效应模拟多点激励，结果表明在大跨度悬索桥设计中，考虑行波效应后对其地震动下结构内力有一定影响，该计算方法和结果可供有关设计人员参考。

1 工程概况

某长江大桥主桥为3跨连续钢桁梁公轨两用悬索桥，跨径为(75+720+75)m；北引桥跨径为(4×43)m，南引桥跨径为(3×43+4×43)m。桥型总体布置如图1所示。桥塔处设置双向活动支座和只受压横向抗风支座，边跨处设置单向活动支座，跨中处设置一对中央扣。

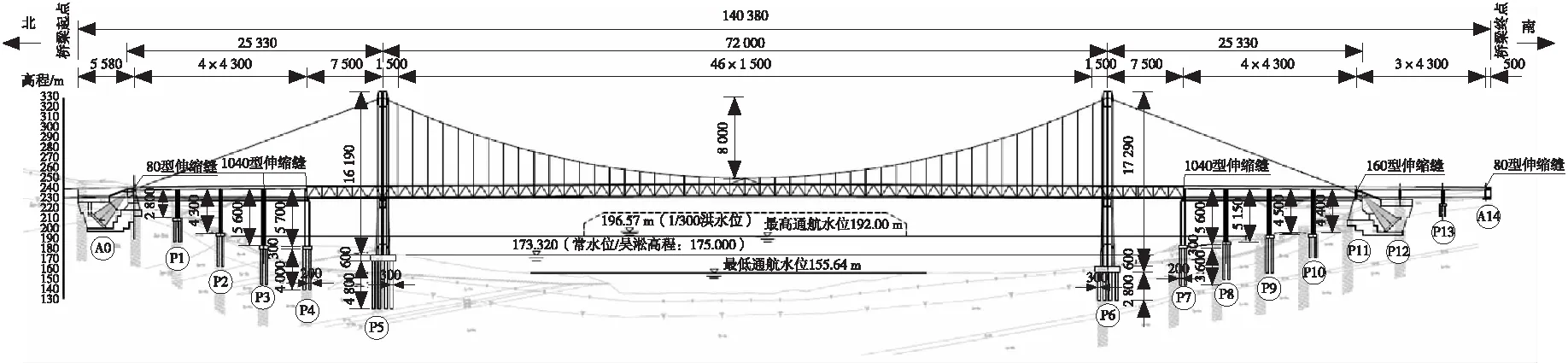
单位：cm

主桥上层桥面宽39 m，下层桥面宽17 m，主桁高12.7 m，标准节间长度为15.0 m，2片主桁中心间距离为17.0 m。桥塔采用C50钢筋混凝土结构，南侧高172.90 m，北侧高161.90 m。主墩承台桩基采用C30混凝土。主缆横向间距为38.0 m，吊索纵向间距为15.0 m。吊索由平行钢丝束制成，标准抗拉强度1 770 MPa。

引桥上部结构为C50等高预应力混凝土连续箱梁，为双箱双室。梁高2.5 m，桥面顶板宽37.0 m。桥墩采用C40混凝土，承台桩基均采用C30混凝土。

2 地震动时程

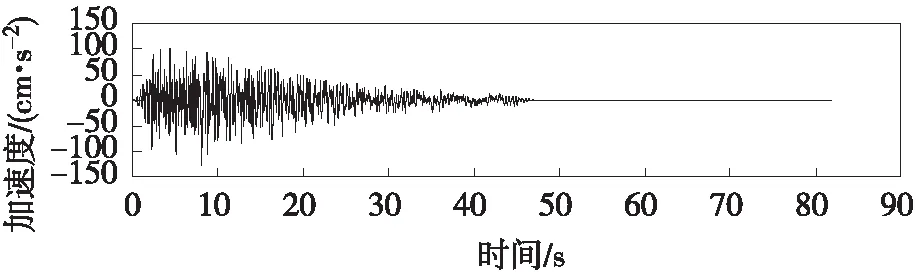
根据JTG D65-05—2015《公路悬索桥设计规范》[9]，抗震分析时，E1、E2地震作用宜分别采用100年超越概率10%和4%地震动组输入。本文E1、E2地震动每组各取3条人工波，分析结果取每组最大值[10]。本桥地震动输入时程如图2、图3所示。其中,E1地震动峰值加速度为0.088g，反应谱特征周期为0.50 s；E2地震动峰值加速度为0.127g，反应谱特征周期为0.55 s。桥位处场地类别为Ⅱ类场地，地震基本烈度为 Ⅵ 度。

3 动力特性分析

采用有限元分析软件对该长江大桥进行非线性时程分析[11-13]，结构阻尼比取0.02，考虑了与主桥相邻1联的引桥结构。主缆、吊杆和中央扣均采用索单元模拟，塔、主梁及桥墩等构件均采用梁单元模拟。主梁与拉索间的连接采用刚性连接，支座采用弹性连接模拟。主桥和引桥群桩基础采用m法计算等代土弹簧模拟桩土效应[14]，动力分析模型如图4所示。

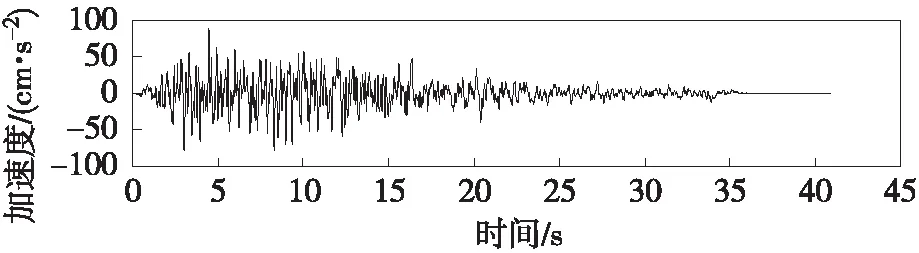
(a) 输入时程1

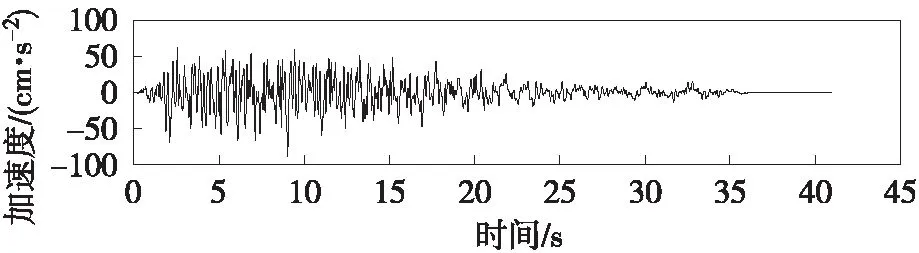
(b) 输入时程2

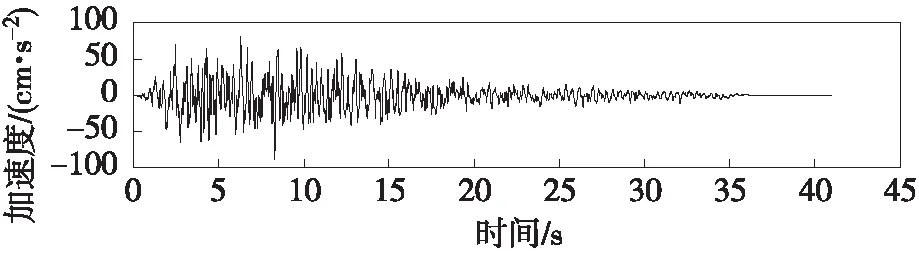
(c) 输入时程3

该长江大桥在成桥状态下前10阶的动力特性计算结果见表1。由表1可知，桥梁的基频为0.148 Hz，基本周期为6.756 s，第1阶振型为主梁对称横弯。

(b) 输入时程2

(c) 输入时程3

图4 某长江大桥动力有限元模型

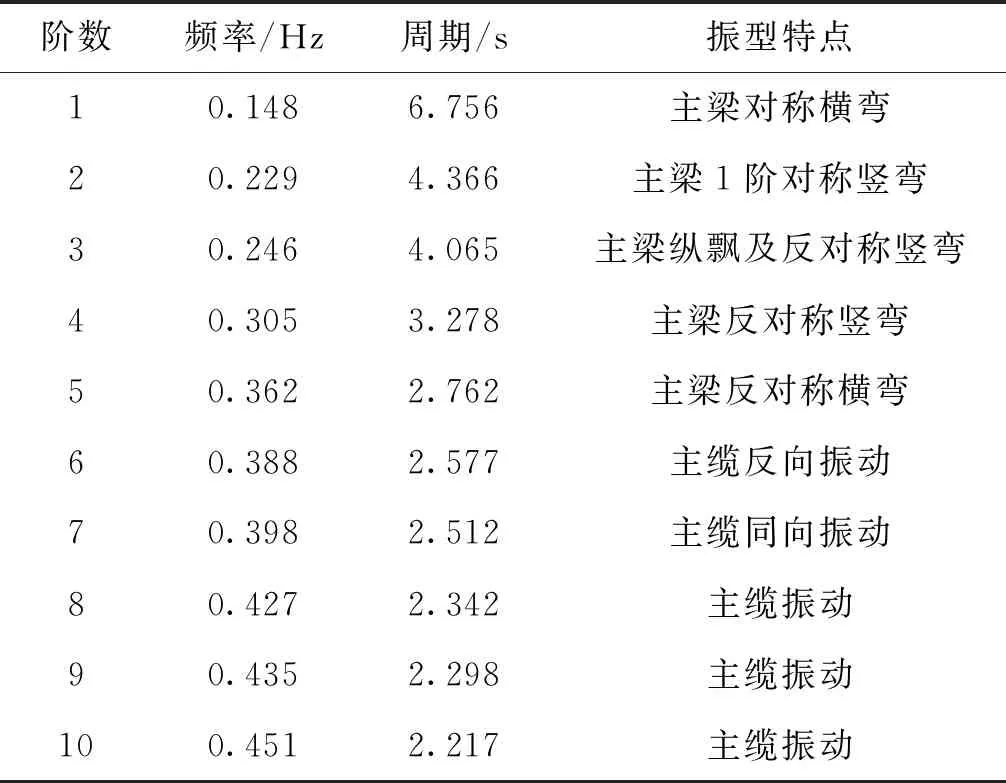
表1 动力特性分析

4 行波效应分析

常用多点激励时程分析有限元模型有2种：一种是位移输入模型；另一种是将地面运动的加速度作为动荷载建立动力平衡方程[15]。本文计算采用位移输入法，即输入位移波时程。根据该桥址处的《工程场地安全评价报告》提供的E2加速度时程波,采用地震波软件将加速度时程进行二次积分转换成位移时程且进行零位修正作为模型的地震动输入，如图5所示。

图5 E2位移波时程地震动

本文以成桥状态下，E2地震作用以纵向+竖向考虑，竖向地震动按水平的0.65倍输入，与恒载组合，选取不同视波速250 m/s～2 000 m/s 分别对全桥模型进行分析。假设地震首先到达北岸桥台处，然后沿纵桥向朝南岸传播，地震动按照到达时间差来输入，不同墩柱地层动行波效应结果见表2。

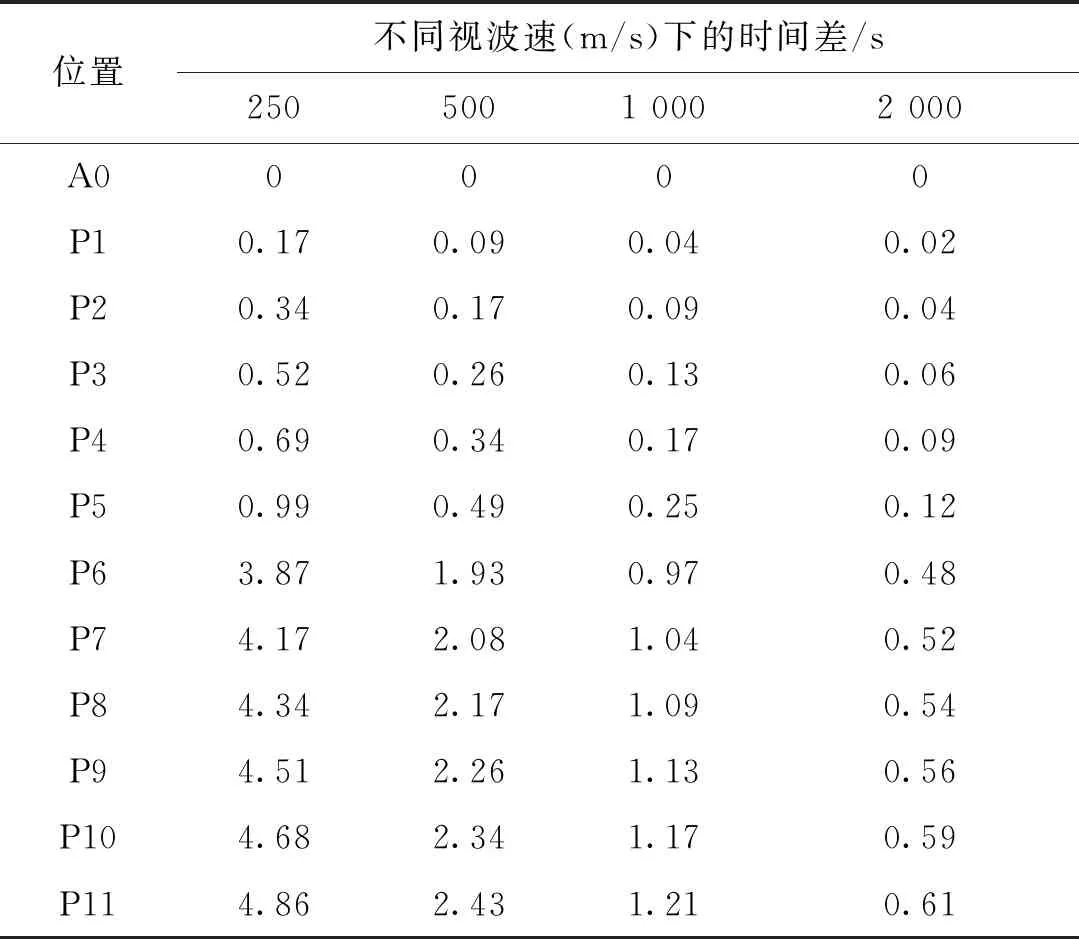
表2 行波效应分析时不同视波速下的时间差

在E2纵向+竖向地震动行波效应作用下，以一致激励内力结果为基准，南北塔柱底部截面计算对比结果见表3。相比考虑行波效应，南北岸塔柱底部截面在一致激励下其剪力和弯矩较大，弯矩最大相差51%，剪力最大相差61%，而塔底轴力变化不大。在行波效应下，南岸塔柱底部截面在视波速V=500 m/s时弯矩、剪力最大；北岸塔柱底部截面在视波速V=250 m/s时弯矩、剪力最大。

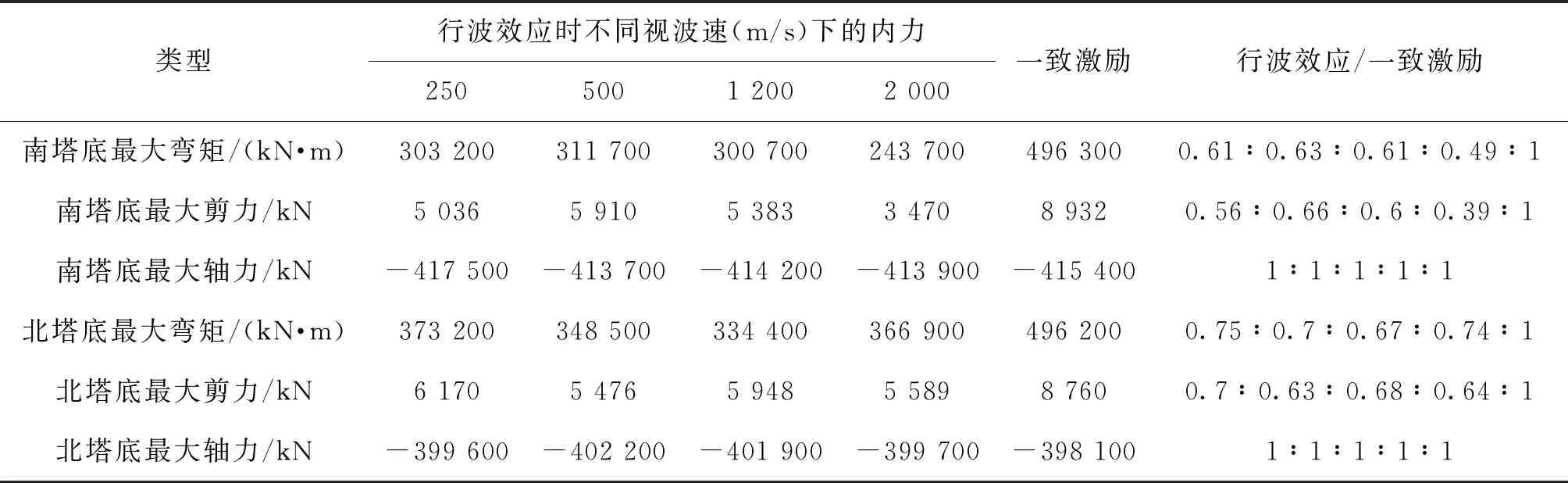
表3 塔底内力在行波效应和一致激励作用下的分析结果对比

由表3可知，行波效应下的塔柱内力较一致激励影响表现为：在E2纵向地震作用及不同波速下，南岸塔底轴力无明显变化，行波效应下塔柱截面的剪力和弯矩小于一致激励作用下的值。

主桥梁端纵向位移在行波效应不同视波速下与一直激励作用下的对比结果见表4。由表4可知，考虑了行波效应后，主桥梁端纵向位移在视波速V=500 m/s时最小，在视波速V=250 m/s时最大。而与一直激励作用下的结果相比，在不同视波速的行波效应下，主桥梁端纵桥向位移减少了20%～70%。

表4 主桥梁端纵向位移在行波效应和一致激励作用下的分析结果对比

索力取各组时程分析中的最大值，主缆与吊杆索力在行波效应不同视波速下与一直激励作用下的对比结果见表5。由表5可知，考虑行波效应与一致激励作用下的索力值变化不大，主缆最大值差异约为2%，而吊杆最大值的差异约为3%。

表5 索力在行波效应和一致激励作用下的分析结果对比

5 结论

本文对某大跨悬索桥进行了行波效应分析，在E2+竖向地震行波效应作用下，对比了不同波速下主桥塔底内力、索力和梁端纵向位移，得出以下结论：

1) 在视波速250 m/s～2 000 m/s范围内，考虑了行波效应的塔底内力、索力均随视波速变化但不显著，且无明显规律。

2) 在不同视波速的行波效应作用下，主桥梁端纵桥向位移结果最大差异约50%，表明主桥梁端纵向位移相对于视波速变化较为敏感。

3) 相比一致激励作用，考虑不同视波速下行波效应作用的塔柱底部内力剪力和弯矩较小，弯矩最大相差51%，剪力最大相差61%，而轴力基本不变；主缆索力减小最大约2%，吊杆索力减小最大约3%；主桥梁端纵桥向位移减少最大约70%。