基于压电驱动器的Stewart微动平台迟滞补偿和解耦控制研究*

何亚林,赵新龙

（浙江理工大学 机械与自动控制学院，浙江 杭州 310018）

0 引 言

Stewart微动平台由动平台、定平台和连杆通过铰链链接而成，可以实现6自由度运动。其作为一种并联机器结构，具有结构刚度大、位置精度高、载重比高等优点，被广泛应用于电子元件生产中的夹持系统、精密机床中的刀具控制和钻铣等领域。

在驱动方面，Stewart平台常采用电液驱动方式。电液驱动方式精度较低，压电驱动器则具有高分辨率、高带宽、执行速度快等特点，能实现亚纳米范围内的运动。然而，压电驱动器固有的迟滞特性会影响平台的控制精度，引起振荡甚至会造成系统不稳定。另一方面，Stewart微动平台具有强耦合性，采用常规的方法难以实现基于压电执行器的Stewart微动平台的精确控制。

在建模方面，用于Stewart平台的动力学方法主要有Newton-Eular法、Lagrange法和Kane法等。其中，Newton-Eular法因比较直观，应用最为广泛。DO等[1]基于Newton-Eular法建立了忽略关节摩擦和支腿轴向转动惯量时的逆动力学模型；DASGUPTA等[2]在充分考虑惯性和支腿摩擦的基础上，提出了改进的Newton-Eular闭环动力学模型；LEE等[3]考虑了支腿的柔性作用,采用Lagrange方法对Stewart平台进行了动力学建模；焦健等[4]采用基于Kane方程的方法，结合虚功原理推导了Stewart平台的动力学方程。对压电驱动的Stewart平台，必须结合迟滞补偿才能更准确地实现压电驱动Stewart平台的建模。

在控制器设计方面，由于Stewart平台的强耦合特性和复杂非线性会影响Stewart平台的工作，造成系统的不稳定，控制器设计问题一直是该平台的研究重点。目前，主要有基于主动干扰抑制（ADRC）的干扰解耦控制和基于干扰观测器（DOB）的控制[5]。但是该类方法需要建立逆动力学模型，控制器参数复杂。YANG[6]通过建立多通道数学模型对耦合特性进行了定性分析，并设计了耦联系统控制器；MA等[7]在利用Kane方法建立了系统多体动力学模型，设计了多体伺服控制器，找出并解决了自由度之间耦合的对应关系；LIN[8]基于等价输入干扰（EID）方法，同时抑制了多个干扰，并且不需要先验扰动信息。

对压电驱动Stewart平台，迟滞特性和耦合特性的相互结合影响控制精度进一步增加了控制器设计的难度，常规的建模和控制方法不再适用。

本文首先引入雅可比矩阵的逆和系统动力学逆模型，在输入端对系统进行解耦；然后用Bouc-Wen模型描述压电驱动器的迟滞特性[9]，利用逆模型方法实现对迟滞特性的补偿；最后在迟滞补偿和输入端解耦的基础上设计控制器。

1 系统建模

Stewart微动平台结构图如图1所示。

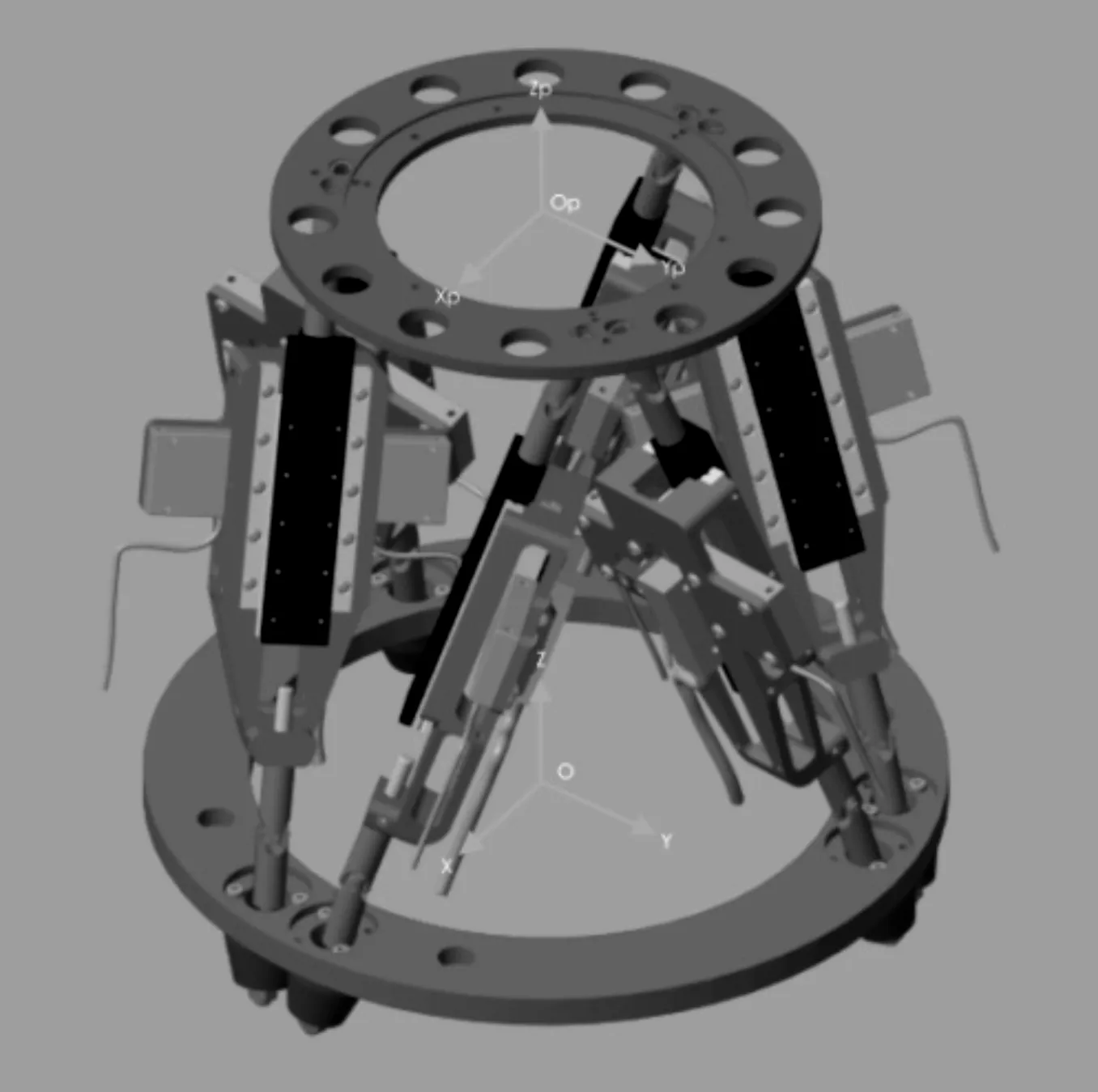
图1 Stewart微动平台结构图

图1中，压电驱动器利用万向节和平台、底座链接，通过伸缩运动驱动动平台运动，从而在三维空间中实现6自由度的运动[10]。

笔者首先建立动坐标系Op-XpYpZp和静坐标系O-XYZ。两坐标系原点分别为动、静平台的质心，坐标平面OpXpYp与动平台重合，坐标平面OXY与静平台重合，Zp轴和Z轴垂直OXY平面竖直向上。

在对平台进行控制时，需要从任务空间转换至关节空间。任务空间采用位姿q=[xpypzpαβγ]T进行描述，关节空间采用l=[l2l2l3l4l5l6]T进行描述。支腿i上端坐标为[PixPiyPiz]T，下端坐标为[OixOiyOiz]T。计算长度时，需要统一坐标系，即通过转换矩阵将动坐标系Op-XpYpZp中的坐标转换到静坐标系O-XYZ中。变换矩阵为：

（1）

式中：Sα=sinα，Cα=cosα，其他类似；xp，yp，zp—动坐标系原点在静坐标系中的坐标；α，β，γ—动平台沿Xp轴、Yp轴、Zp轴的旋转角度。

将动坐标系中的坐标转换至静坐标系后为：

（2）

根据支腿两端坐标，可得支腿长度为：

（3）

采用拉格朗日方程法建立6自由度动力学模型为：

（4）

（5）

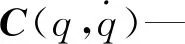
q=[q1q2q3q4q5q6]T=[xpypzpαβγ]T

（6）

F=[F1F2F3F4F5F6]T

（7）

（8）

M=diag[mmm]I=diag[IxIyIz]

（9）

式中：m—上平台质量；Ix，Iy，Iz—上平台绕3个坐标轴x、y、z的转动惯量。

式（4～5）中各个算式的具体表达式为：

（10）

（11）

（12）

（13）

（14）

然后对压电驱动器采用Bouc-Wen迟滞模型[11-12]进行描述，其数学关系为：

（15）

式中：A—控制幅度；B、T—控制迟滞环的形状[13]的参数；k—增益；U—压电驱动器的输入电压；η—中间变量。

联立式（4，5，15），基于压电驱动器的Stewart微动平台的完整数学模型为：

（16）

2 控制器设计

基于输入端解耦和迟滞补偿的Stewart控制系统原理图如图2所示。

图2 系统原理图

首先笔者通过位姿反解，完成从任务空间到关节空间的转换。根据支腿两端在动、静坐标系中的坐标计算可得到预期支腿长度lr。

再引入系统的逆模型进行解耦[14]，通过雅可比矩阵的逆和系统动力学逆模型完成解耦过程。fr表示期望输出驱动力，即：

（17）

对Bouc-Wen迟滞模型逆运算，得:

（18）

最后，将反馈回的实际驱动器驱动力f和实际支腿长度l与预期值进行比较，通过积分分离PID控制算法形成闭环控制，以保证系统的稳定性。

3 仿真及结果分析

为了验证控制器的有效性，笔者对定点运动（即阶跃响应）和连续运动进行仿真分析，采用积分分离PID控制器形成闭环控制。其参数取Kp=4×104，Ki=90，Kd=1×103。迟滞补偿器参数取A=1.2，B=0.05，T=0.01，k=1.5。

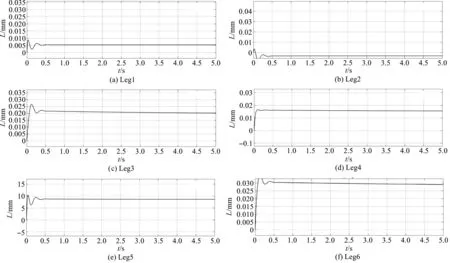
图3 定点运动响应曲线

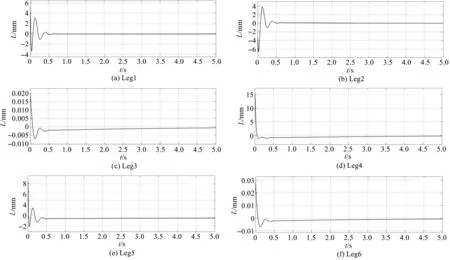
图4 定点运动误差曲线

（2）期望轨迹为正弦函数拟合的周期性连续运动，即位姿为：

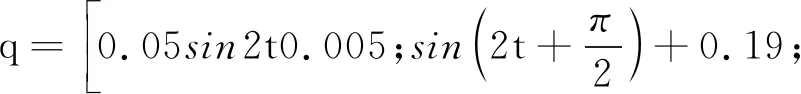
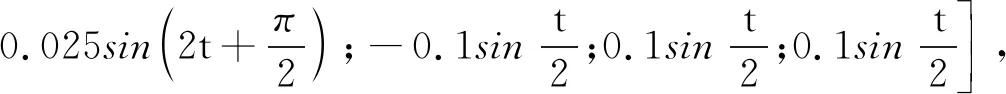
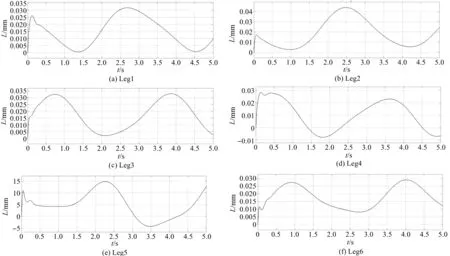
图5 连续周期运动响应曲线

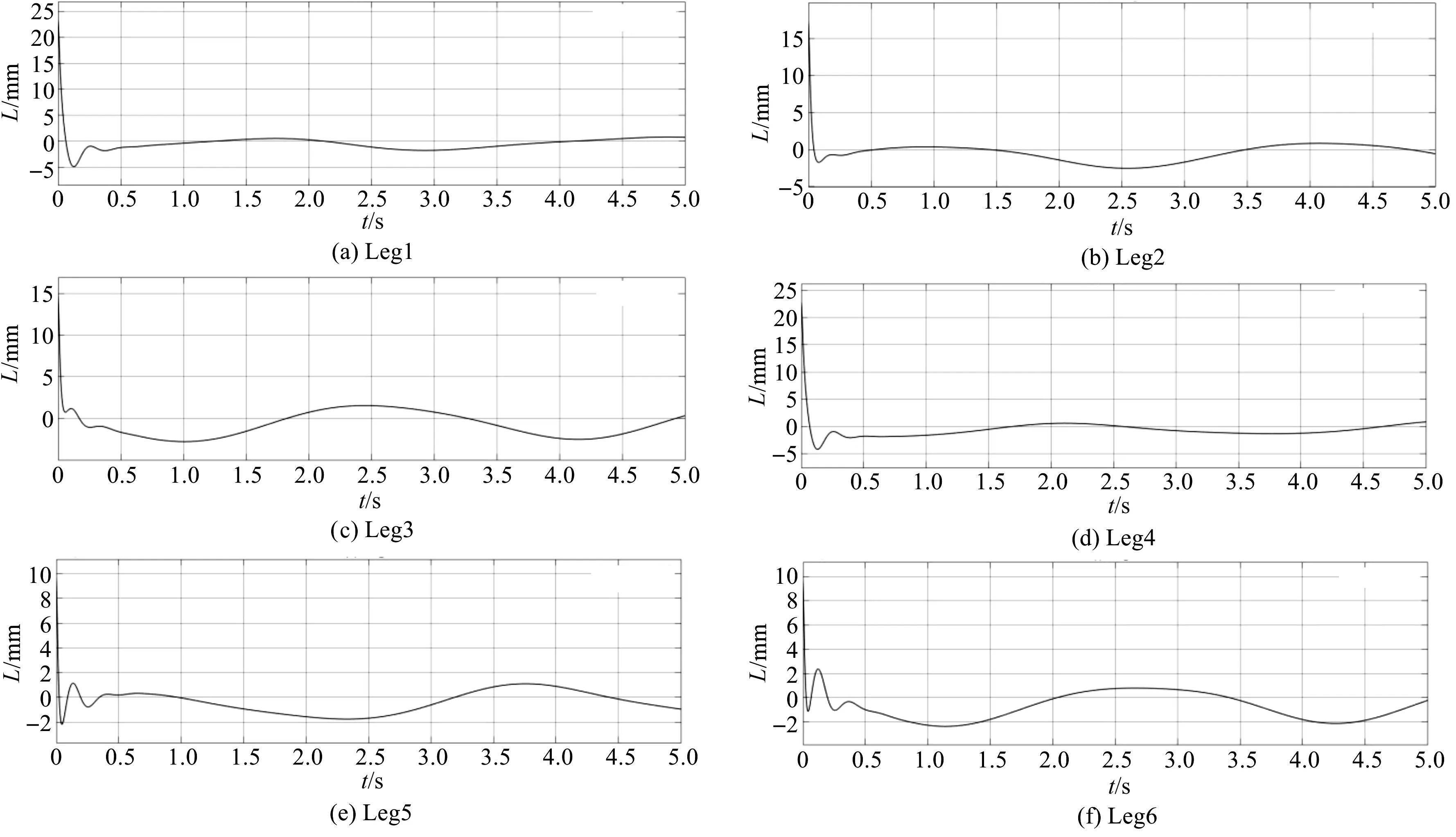
图6 连续周期运动误差曲线

由此可见，在经过解耦控制和迟滞补偿后，系统的响应曲线良好。

由图（3，4）可知：在0.5 s左右，定点运动到达指定位姿，并且误差接近于0；响应速度较快且最终误差几乎为0。

由图（5，6）可知：当平台启动后，在进行连续周期运动时，6个支腿长度变化曲线也呈周期性变化，动态定位误差皆为5%以内，且不会引起系统振荡，可见达到了稳定的控制效果。

4 结束语

针对压电驱动器的Stewart微动平台同时存在强耦合性和迟滞特性的特点，笔者采用拉格朗日方程法建立了压电驱动Stewart平台动力学模型，先通过旋转变换矩阵进行位姿反解，得出了Stewart平台各支腿长度，再设计了基于平台的输入端解耦和迟滞逆模型补偿的控制器，对Stewart微动平台实际输出进行了定点运动状态和连续运动状态的跟随。

最终的实验结果表明，该控制器能对Stewart平台实现稳定良好的控制效果。