一种闭锁机构的闭锁力影响因素的研究*

余 芳，李 屹*，李家春，吴 兵，张建明

（1.贵州大学 机械工程学院，贵州 贵阳 550025；2.贵州哈雷空天环境工程有限公司，贵州 安顺 561000）

0 引 言

闭锁机构是火箭发射系统中防止弹体前后移动及对火箭弹进行定位的关键装置，其闭锁性能的好坏直接影响到火箭发射的效率、射击精度以及运输过程的安全。若机构闭锁力太大，弹体点火发射瞬间初始扰动会增大，发射的精度及效率会受到影响；闭锁力太小，同样会导致定位精度差，也不能进行有效定位，且当机构闭锁力小于弹体发射所需的最小闭锁力时，在运输过程中会由于弹体自重、惯性等多重因素导致弹体非正常脱落，将造成意外事故。所以合理及精确的闭锁力设计是闭锁机构设计的关键问题之一。

当前对闭锁力的设计值定义还存在分歧，陈四春等[1]用有限元方法对某型闭锁机构进行了分析研究，提出了闭锁力的设计值应为定向钮稳定运动且运动速度达到火箭弹设计初速1%时发动机的推力值；姜勇等[2]用理论推导结合有限元方法对某型闭锁体进行了分析研究，提出了卡簧式闭锁器产生的闭锁力很不稳定，实际值跳动很大，因此不能以闭锁挡弹器的最大约束力作为有效闭锁力，应该把约束力跳动之前的稳定值作为有效闭锁力；武秋生等[3]通过有限元方法对发射条件下定向钮与闭锁机构之间相互作用历程进行了分析，认为应将定向钮所受最大约束力作为闭锁机构的闭锁力。

火箭弹质量和闭锁机构的工作原理是闭锁力设计的主要依据[4]，不同工作原理的闭锁机构，对闭锁力的影响因素也不同。为了获得设计所需的闭锁力，在闭锁机构设计时，常规设计大多是先根据理论分析计算，试制出机构实物后，再采用静态法对闭锁力进行测试。若理论分析计算的准确性较差，则这一过程需要多次反复。

针对这一问题，本文将应用有限元分析方法，结合Abaqus/Explicit显示非线性动态法对某型闭锁机构的挂钩脱钩过程及主要影响因素进行数值模拟，研究分析主要影响闭锁机构闭锁力大小的3种因素。

1 闭锁机构结构及受力分析

1.1 闭锁体结构

常用的弹体闭锁机构有4种：摩擦式、弹簧式、杠杆式以及剪切销式闭锁机构[5]。本文研究的机构属于弹簧式闭锁机构，其简化模型如图1所示。

图1 闭锁机构简化模型1—主弹簧钢垫片；2—副弹簧钢片；3—副弹簧钢垫片；4—挂钩；5—螺钉；6—螺钉；7—螺钉

该闭锁机构主要由主/副弹簧钢片、副弹簧钢垫片、挂钩和螺钉等组成。其中，主/副弹簧钢片为柔性体，挂钩、螺钉及副弹簧钢垫片在研究时可视为刚体；挂钩与主弹簧钢片接触用螺钉固定连接，副弹簧钢垫片与主弹簧钢片接触用螺钉固定连接，主/副弹簧钢片尾部接触，并一起用螺钉固定在炮管上。

1.2 闭锁机构工作原理

闭锁机构主要闭锁方法有两种:利用弹簧能量闭锁和利用闭锁体自身弹性进行闭锁[6]。本文研究的机构属于第2种，其简化模型如图2所示。

图2 闭锁机构工作原理简化模型1—火箭弹尾部沟槽；2—闭锁体挂钩；3—火箭弹；4—固定点；5—第194号节点

该闭锁体挂钩底部卡入火箭弹尾部沟槽内，通过主/副弹簧自身的弹性进行闭锁，防止火箭弹前后移动。火箭弹点火发射时，火箭弹受到推力与闭锁体发生高速碰撞。当推力加载到足够大时，火箭弹向右移动，强制迫使主/副弹簧钢片围绕其固定点A沿Y轴正向顺时针变形转动，直到火箭弹完全挣脱闭锁机构。

1.3 火箭弹脱钩受力分析

火箭弹燃烧室点火发射时，弹体冲击挂钩机构向前脱钩受力示意图如图3所示。

图3 机构向前脱钩受力示意图

设挂钩底部受到火箭弹向右的外载荷冲击力为F1，在外载荷的作用下挂钩与弹体接触面正压力为FN，弹体脱钩过程中闭锁机构的变形量及速度与火箭弹推力F1相关。闭锁机构所承受的最大推力（闭锁力）与机构零件材料、钢片厚度和宽度等因素有关。

根据弹体发射时受力情况，则有：

FN-F1sinα=0

（1）

式中：α—水平载荷F1与挂钩接触面之间夹角（α在弹体挣脱挂钩过程中呈规律变化）。

fF1sinα-F1cosα=0

（2）

式中：f—弹体与挂钩接触面的摩擦系数。

2 建模及边界设置

2.1 计算方法

闭锁机构闭锁力分析除考虑机构零件材料及众多因素外，还涉及到刚性体与刚性体接触面的接触和碰撞、刚性体和柔性体的面接触、柔性体和柔性体的面接触及螺栓的紧固连接等问题。针对碰撞过程中复杂的接触问题以及柔体的变形特性，考虑到收敛问题，为提高求解的效率，本文采用Abaqus/Explicit显示非线性动态分析方法。

程序求解动力学平衡方程为:

Mu=P-I

（3）

式中：M—节点质量矩阵；u—节点加速度。

u=（M）-1（P（t）-I（t））

（4）

式中：P—所施加外力；I—单元内力；t—增量步开始时刻。

σ（t+Δt）=f（σ（t）,dε）

（5）

式中：б—单元应力；ε—应变率；dε—应变增量[7]。

2.2 网格划分

本研究采用SolidWorks软件对整个机构进行一比一数字化建模，用hyper mesh对模型进行网格划分等前处理。针对机构各零部件的特殊接触，笔者对柔性变形体部分主弹簧钢片/副弹簧钢片及弹簧钢垫片进行六面体网格划分，对刚性体挂钩部件进行四面体和六面体网格划分，模拟弹与挂钩接触部分进行六面体网格划分，划分节点数为229 157，单元数为211 200。

2.3 边界条件定义及材料参数

笔者对主/副弹簧钢片尾部进行固定约束，挂钩和主/副弹簧钢片一起随着主/副弹簧钢片发生挤压变形而围绕主弹簧钢片尾部固定点在XOY平面顺时针转动，模拟弹沿X轴正向移动，对其余运动方向进行约束，螺栓与各零部件的连接采用绑定约束。

机构中各零件接触定义如表1所示。

表1 机构各部件接触定义

材料参数按各零部件实际情况进行设定。变形部分柔性体为弹簧钢，主/副弹簧钢片及弹簧钢垫片采用一套材料参数，设置密度ρ=7 850 kg/m3，弹性模量E=2.07×1011Pa，泊松比u=0.3；挂钩部分设置密度ρ=2 600 kg/m3，弹性模量E=7×1010Pa，泊松比u=0.33；火箭弹与挂钩接触面设置密度ρ=8 500 kg/m3，弹性模量E=1.05×1011Pa，泊松比u=0.34。[8]

3 仿真结果与分析

3.1 火箭弹脱钩过程模拟

弹体从火箭弹燃烧室点火受到冲击撞击挂钩，到弹体挣脱闭锁体的脱钩过程如图4所示。

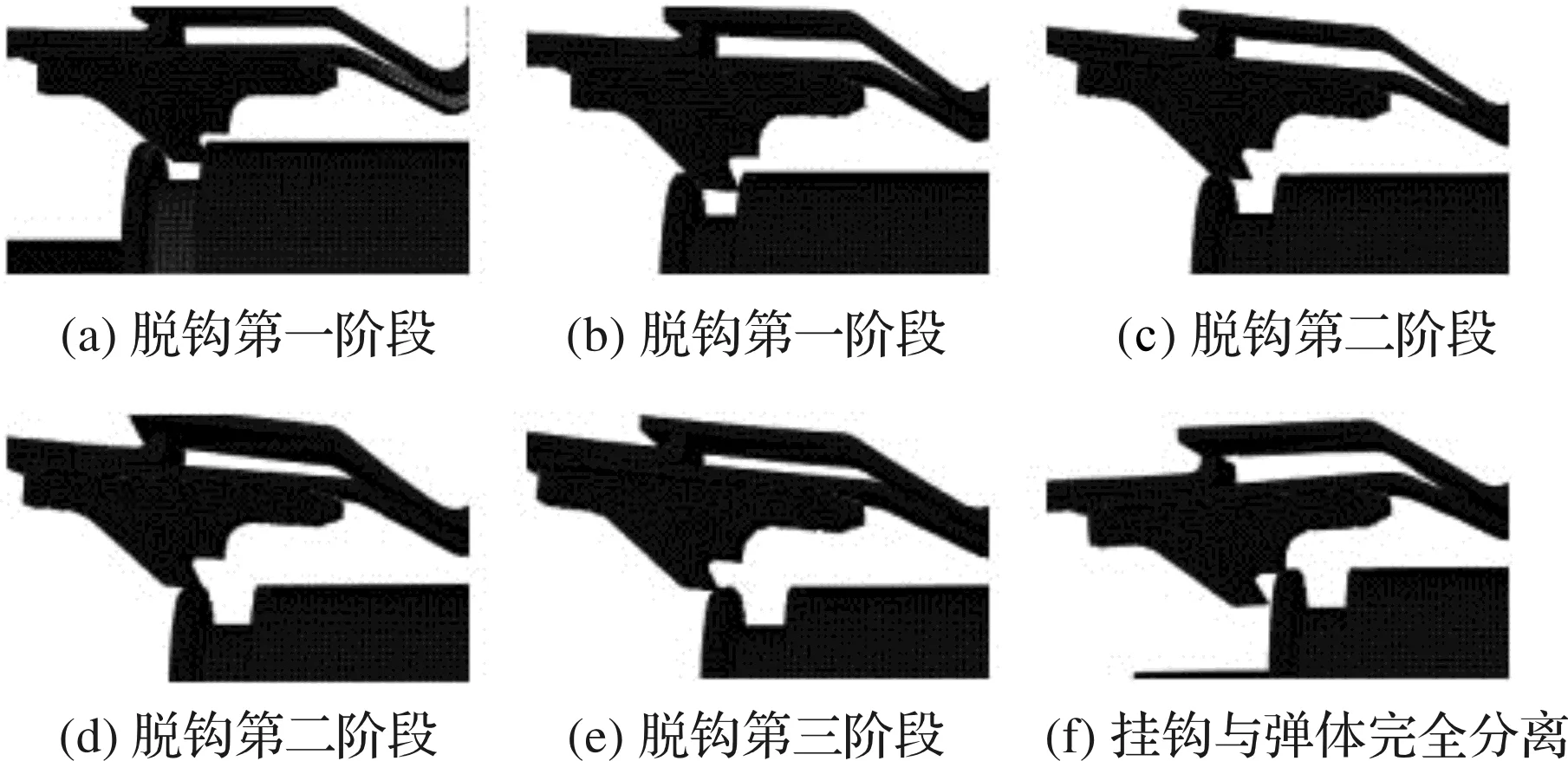
图4 火箭弹脱钩过程

整个脱钩过程可分为3个阶段：

（1）第一阶段。火箭点火冲击弹体，弹尾部沟槽左侧环面与挂钩底部左侧倾斜面接触，该阶段弹体受到的推力小，与挂钩侧面的摩擦力大，闭锁机构变形大，该阶段时长约占整个脱钩过程时间的67%左右；

（2）第二阶段。火箭弹尾部表面与挂钩底部正面接触，该阶段火箭弹推力相较第一阶段明显增大，火箭弹速度变化快，对闭锁机构的冲击明显；但由于挂钩上与弹体接触的表面与弹体运行方向一致，闭锁机构变形较小，此阶段时长为全过程33%左右。

（3）第三阶段。火箭弹表面与闭锁机构完全分离，弹体速度达到设计要求，欲挣脱闭锁机构即将分离的瞬间，此时机构闭锁力达到最大值。

3.2 弹体脱钩过程影响因素分析

根据前期研究和相关文献资料[9-14]，本文选取影响较大的几种因素进行数值模拟，研究其对弹体速度、脱钩时间、闭锁力、闭锁体变形位移量等参数的影响。

分析中，取火箭弹刚好与闭锁体挂钩完全分离时刻，火箭弹推力为该闭锁机构闭锁力。由于闭锁体变形不规则，为分析方便，笔者统一采用挂钩底部第194号节点在Y轴方向位移来分析闭锁体变形程度。

3.2.1 摩擦系数对脱钩过程的影响

本研究采用质量为40 kg的火箭弹，0～30 ms内火箭弹发动机推力随时间变化的拟合函数为F（t）=126 590t（F—火箭弹发动机推力，t=0—点火时刻）。本文通过改变闭锁机构挂钩与火箭弹接触面材料和表面情况来改变摩擦系数，模拟分析火箭弹与挂钩接触部分摩擦系数对弹体脱钩过程及闭锁力的影响。

弹体与挂钩接触面摩擦系数f变化时,火箭弹从点火开始至脱钩过程中不同摩擦系数火箭弹速度变化曲线如图5所示。

图5 不同摩擦系数火箭弹速度变化

从图5可以看出：随着摩擦系数增加，相同载荷下弹体与挂钩之间的摩擦力增大，弹体速度随时间（或推力F1）变化的速度变慢，从而导致弹体脱钩时间增加，脱钩闭锁力增大；当摩擦系数由0.1增加到0.3时，弹体脱钩时间从12.9 ms增加到14.69 ms，机构闭锁力从1 639 N增大到1 860 N。

但在不同的时段，摩擦系数的变化对弹体运行情况的及闭锁体变形情况的影响程度不同。不同摩擦系数194节点Y方向位移如图6所示。

图6 不同摩擦系数194节点Y方向位移

从图6可以看出：在自点火开始的较短时间（大约0～3 ms）内，火箭弹速度增加非常缓慢，摩擦系数的变化对速度的影响不明显。这是因为点火初期，弹体所受推力小，摩擦系数的变化引起的摩擦力（大小为fF1sinα）对弹体速度的影响小。

摩擦系数对应脱钩时间及闭锁力如表2所示。

表2 摩擦系数对应脱钩时间及闭锁力

从表2可以看出：（1）在第一阶段，弹体作用在闭锁体上的冲击力随时间增加，闭锁体变形量增大很快（由挂钩上讨论点在Y轴上的位移量体现）；（2）在第二阶段，闭锁体挂钩位移曲线变缓，这是由于接触面变换，闭锁机构变形虽然继续，但变形增加变慢；（3）在第三阶段，弹体施加在闭锁体上的推力消失，在惯性作用下闭锁体变形继续增大，直至最大值，然后快速回复（图6中摩擦系数为0.1和0.15的两条位移曲线末端已经开始下垂，进入回复阶段）。

与弹体速度的变化趋势及原理类似，随着摩擦系数的增加，闭锁体变形速度变慢，达到最大位移时间增加；在点火开始时，闭锁体受到的冲击力小，摩擦系数不同引起的摩擦力对闭锁体变形情况的影响不明显，几条挂钩讨论点的位移曲线几近重合；随着弹体施加到闭锁体的推力越来越大，摩擦系数变化引起的摩擦力变化对闭锁体变形的影响变得明显。

从图中可以看出，大致在7 ms以后，摩擦系数越小，在相同时刻，挂钩讨论点的位移越大[15-16]。在脱钩过程的第二阶段，由于摩擦力对闭锁体变形的影响变小，一方面，闭锁体变形变缓；另一方面，前阶段因为摩擦系数大而位移较小的曲线比摩擦系数低的位移曲线陡，即闭锁体变形比接触面摩擦系数低的闭锁机构要快。

3.2.2 加载载荷对脱钩过程的影响

根据赵良玉等[17]对火箭弹发动机推力优化的5种最优方案，笔者选取前4种作为火箭弹点火施加的推力载荷，其火箭弹推力拟合函数分别为F（t）=799 652t；F（t）=126 590t；F（t）=105 049t。

F（t）=87 800t,t=0为点火时刻，分别施加到质量为40 kg火箭弹上，设定火箭弹与挂钩接触部分摩擦系数均为0.15，分析火箭弹发动机推力不同对弹体脱钩过程的影响。不同载荷火箭弹速度变化和不同载荷194节Y方向位移如图（7,8）所示。

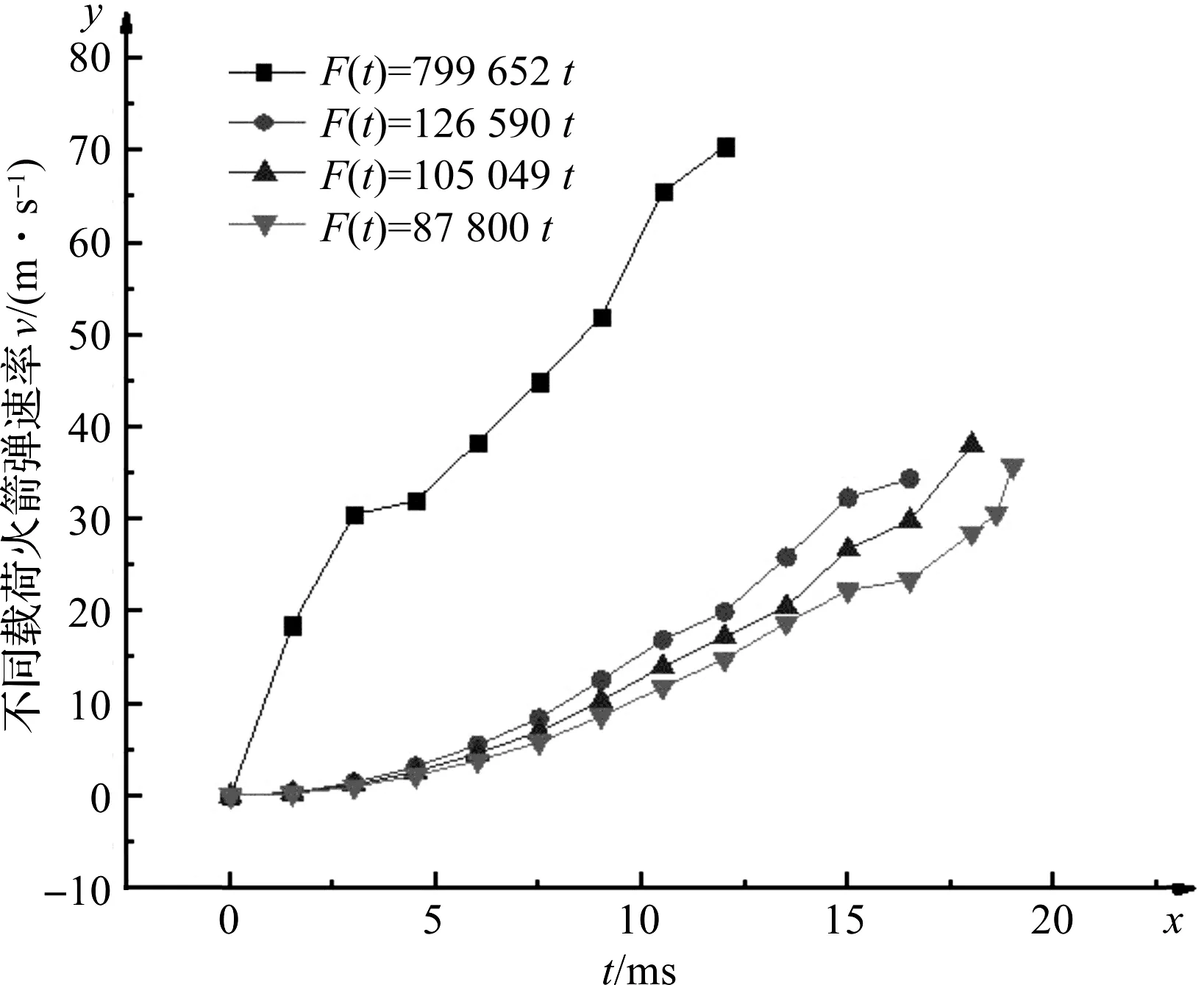
图7 不同载荷火箭弹速度变化

图8 不同载荷194节点Y方向位移

从图（7,8）可以看出：载荷越大，弹体的速度上升越快；在0～5 ms内，载荷最大的曲线上升变化很快，另外3条曲线变化缓慢且无明显区别，此时间内，加载最大载荷的弹体已经与挂钩完全分离；5 ms以后，载荷较小3条曲线增加变化趋势相似，但载荷最大的变化快，载荷最小的变化较缓。

最大载荷的位移曲线最陡，载荷F（t）=126 590t的曲线在接近5 ms时开始明显变陡，载荷F（t）=105 049t曲线在7 ms左右变形速度加快，而载荷F（t）=87 800t曲线缓慢变化到接近14 ms左右时速度才明显加快。

载荷越大，弹体碰撞闭锁体时相互作用越明显，挂钩随着载荷增加变形速度越快，脱钩时间减短，闭锁力有增加趋势。

不同载荷脱钩时间和闭锁力如表3所示。

表3 不同载荷脱钩时间和闭锁力

3.2.3 不同质量弹体对脱钩过程的影响

笔者用不同质量火箭弹对闭锁机构进行脱钩模拟。火箭弹与挂钩接触部分摩擦系数设为0.15，推力载荷0～30 ms内随时间变化函数为F（t）=126 590t（t=0—点火时刻）,不同质量火箭弹速度变化如图9所示。

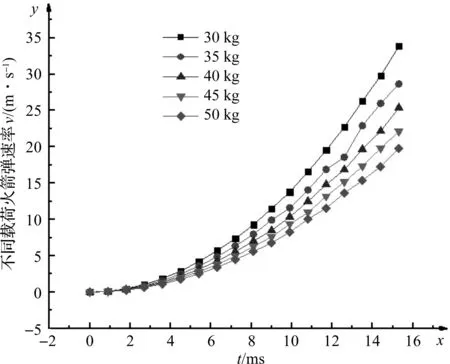
图9 不同质量火箭弹速度变化

从图9可以看出：1 ms～5 ms火箭弹速度增加缓慢，5 ms以后不同质量弹体的速度变化开始加快；随着火箭弹推力增加，不同质量火箭弹速度变化开始拉大，质量越大，速度增加越缓慢，弹体质量增加，其速度变化越慢。

节点位移变化趋势其变化情况与图9速度变化相关，不同质量194节点Y方向位移如图10所示。

图10 不同质量194节点Y方向位移

从图10可以看出：在0～5 ms，该时间段火箭弹推力小，不同质量弹体位移速度都非常缓慢；5 ms～9 ms，随着弹体推力增加，位移曲线变化开始加剧；9 ms以后变化又开始放缓，这是由于弹体与挂钩接触处于第二阶段，挂钩位移量减小；弹体质量为30 kg最快达到最大位移并出现拐点，质量越大达到最大变形量时间越长。

不同质量火箭弹对应脱钩时间和闭锁力如表4所示。

表4 不同质量脱钩时间和闭锁力

从表4中可以看出：随着质量增加，脱钩时间和闭锁力有增加趋势，但变化范围不大，尤其是当质量达到40 kg以后，脱钩时间和闭锁力增加量越来越小。

4 实验测试验证

本文采用某企业自行研发的闭锁力测试装置，对某闭锁机构的闭锁力进行测试分析，以验证数值模拟分析的正确性。

4.1 实验设备及工作原理

设备执行部分主要由伺服电机、丝杠、拉压力传感器等组成。由西门子plc1200控制器驱动两台伺服电机同时联动，通过丝杠快速拉动模拟火箭弹直到弹体完全挣脱闭锁机构，通过拉力传感器传输给控制器的数据可以得出闭锁机构最大闭锁力。

4.2 测试数据与仿真结果对比

由于弹体表面材料已经定型，摩擦系数的改变只能通过改变闭锁机构的挂钩材料及表面，实验周期较长。火箭弹推力的加载是根据技术指标来设计，改变加载火箭弹的推力实验成本高，故本文只对改变弹体质量对闭锁力的影响进行实验。

本文用某型30 kg、35 kg及40 kg的模拟火箭弹进行现场测试实验，通过控制器驱动伺服电机模拟火箭弹发动机的推力拟合函数为F（t）=126 590t，采用摩擦检测仪测出挂钩与弹体接触面的最大静摩擦系数为0.15，得出拉力传感器在模拟弹脱离挂钩过程中最大拉力数据。

不同质量实验测试闭锁力数据如表5所示。

表5 不同质量实验测试闭锁力数据

从表5中可以看出：相同样本每次测出的闭锁力结果并不完全相同，而是在一个较小的范围内波动；实际测试结果平均值和数值模拟结果吻合度好，最大误差为1.5%，属于产品设计允许范围。

5 结束语

本文应用有限元分析方法，对某型闭锁机构的挂钩脱钩过程及主要影响因素进行数值模拟，模拟结果表明，火箭弹与挂钩接触部分摩擦系数、弹体加载载荷函数及弹体质量对弹体脱钩过程，及闭锁机构的闭锁力均有不同程度的影响。主要结论如下：

（1）在火箭弹整个脱钩过程中，摩擦力对脱钩过程第一阶段影响较明显，摩擦系数越大，火箭弹速度增加越缓慢，脱钩时间越长，闭锁力有缓慢增加趋势；

（2）加载载荷对脱钩过程的影响贯穿整个脱钩过程，载荷越大，闭锁体变形响应速度越快，脱钩时间越短，推力越大，弹体与挂钩碰撞相互作用明显，闭锁力呈缓慢增大趋势；

（3）火箭弹质量对脱钩过程的影响主要体现在脱钩时间和火箭弹脱钩速度，质量越大，火箭弹速度增加越慢，脱钩时间越长，闭锁力越大。

实验测试结果与模拟分析的结果吻合度好，误差属于可以接受的范围，这说明数值模拟的结果可信。