从向量到实函数的傅里叶变换探析

王治

从向量到实函数的傅里叶变换探析

王治

（武警警官学院 基础部，四川 成都 610213）

从介绍向量空间中内积引申出向量的傅里叶展开，然后从向量空间过渡到实函数空间，从可积函数内积得到实函数的傅里叶展开．探讨向量空间中向量和实函数空间中函数的傅里叶展开，并讨论二者之间的联系，对理解基向量、基函数和傅里叶变换有一定的价值．

基向量；向量空间；函数空间；傅里叶展开

傅里叶是举世闻名的法国数学家和物理学家．傅里叶的科学成就，主要在于他对热传导问题的研究，以及他为推进这一方面研究所引入的数学方法．相关研究理论对19世纪数学的发展产生了巨大的影响[1]．傅立叶的工作意义远不止此，他迫使人们对函数概念作修正、推广，特别是引起了对不连续函数的探讨．傅里叶级数实际上是函数按照基函数展开的，而向量空间也可以定义基，甚至正交基和标准正交基．从而向量空间中的向量可以和实函数空间中的函数一样，按照基展开，这就是向量的傅里叶展开．也就是向量空间中的任何一个向量都能由基向量组来线性表示[2]．同样在数学中，基函数是函数空间一组特殊基的元素，函数空间中的连续函数都可以表示成一系列基函数的线性组合．函数空间中基函数的确定并不是唯一的．

傅里叶的三角级数理论是从研究偏微分方程起步的．傅里叶级数理论一经形成就对整个数学产生了深刻的推动作用[3]．数学上除了我们熟知的三角级数展开之外，研究学者还发现了更多的基函数，像贝塞尔基函数、多项式基函数、高斯基函数和勒让德基函数等．目前基于傅里叶变换的研究存在于生活和科学的各个领域，如光纤传感信号的识别、宽带信号的传播、家纺图案生成技术和保密通信安全性分析等，这些研究都可以帮助我们更好地理解傅里叶级数的内涵[4]．

本文探讨向量空间中向量和实函数空间中函数的傅里叶展开，并讨论二者之间的联系，对理解基向量、基函数和傅里叶变换有一定的价值．

1　向量的傅里叶展开

向量空间的任何一个基都可以通过Gram-Schmidt正交化过程转化为正交基，再单位化就可以得到一个标准正交基．

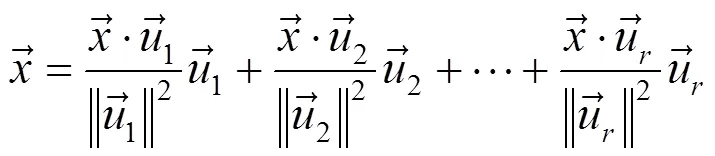
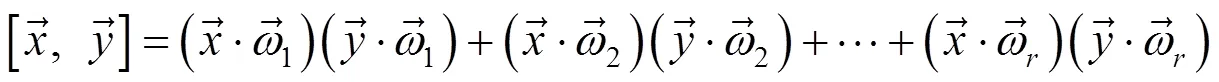
2 实函数的傅里叶展开

数学上，只有满足一定条件的函数（即函数要无穷次可导）才可展开成幂级数，这个条件要求较高，而傅里叶展开的条件相对容易达到，很大一类函数都能满足．函数展开为傅里叶级数的主要目的，不只为了用一个三角多项式来近似表示其和函数，更多的目的在于它的实际应用．连续函数常用正弦函数或余弦函数的线性组合来逼近[6]，如一个连续函数可以表示一个声波、某类电信号或力学振动系统的运动等．

当然实函数和复函数是有区别的，这里只针对实函数进行讨论．可以帮助学生从更高的角度去理解傅里叶级数的内涵，并且对于理解其它形式的函数展开也是有帮助的[10]．

3 结语

通过本文的理论探讨，比较向量空间的基向量和实函数空间的基函数，基向量和基函数的正交化、标准化过程，从而得到向量空间中向量的傅里叶展开和实函数空间中函数的傅里叶展开，对今后研究相关问题有理论上的借鉴价值．在学习的过程中，系统地梳理这些问题，有利于更好地掌握傅里叶级数内容和与其相关的一些专业课程．

[1] 武娜．傅里叶级数的起源和发展[D]．石家庄：河北师范大学，2008：47

[2] 同济大学数学系．线性代数[M]．6版．北京：高等教育出版社，2014：104-107

[3] 贾随军，胡俊美．傅里叶级数理论成因分析[J]．咸阳师范学院学报，2017（6）：21-28

[4] 李文新．函数展开成Fourier级数的几何解释[J]．南昌师范学院学报，2005，26（3）：5-6

[5] 同济大学数学系．高等数学[M]．北京：高等教育出版社，2014：307-310

[6] 魏全顺．关于函数的Fourier级数系统展开方法[J]．湖南第一师范学报，2007，7（1）：158-160

[7] 陈纪修，於崇华．数学分析[M]．北京：高等教育出版社，2004：409

[8] 夏道行，吴卓人，等．实变函数论与泛函分析[M]．北京：高等教育出版社，2010：216

[9] 刘深泉，张万芹，陈玉珍，等．线性代数及其应用[M]．北京：机械工业出版社，2019：384-386

[10] 汤一．探究基向量、基函数与傅里叶级数之间的联系[J]．课程教育研究，2018（37）：136

Analysis of Fourier transform from vector to real function

WANG Zhi

（Department of Foundation，Officers College of CAPF，Chengdu 610213，China）

From the introduction of inner product in vector space，the Fourier expansion of vector is extended，then from vector space to real function space，the Fourier expansion of real function is obtained from the inner product of integrable function．The Fourier expansion of vector in vector space and the Fourier expansion of function in real function space is discussed，and the relationship between them is discussed，which is of certain value to understand the basis vector，basis function and Fourier transform．

basis vector；vector space；functional space；Fourier expansion

O174.2︰G642.0

A

10.3969/j.issn.1007-9831.2020.03.018

1007-9831（2020）03-0092-03

2019-11-13

王治（1987-），男，山西太原人，讲师，硕士，从事工程数学教学研究．E-mail：wang111zhi@126.com