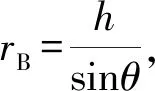从两个形似的速度关联问题说起

王 芳

(江苏省木渎高级中学,江苏 苏州 215100)

速度关联问题是运动的合成和分解中的重难点，对于用轻绳、轻杆相连的系统,学生会抓住两物体的实际速度为合速度,并将其按沿绳(杆)和垂直于绳(杆)这两个方向分解,取其沿绳(杆)方向的分速度相等,往往就能轻松解决问题。但是，对于下面两个看上去很形似的问题,学生常用的解题套路却失效了。

1 两道形似题引发的思考

图1

针对速度关联问题的两道形似题的解答如图1、2所示，图1中学生的解答是错的,图2中学生的解答却是对的。两题都是与杆相关的速度关联问题,看上去很相似。学生采用同样的处理方法,将平台或物块的速度沿杆和垂直于杆的方向进行分解,然后取其垂直于杆的分量和杆上接触点的线速度相等。对错结果不同，问题到底出在哪里?学生百思不得其解。

图2

2 对速度关联问题的分析

对于两个刚体(形状、大小都不发生变化的理想模型)或质点,当它们直接接触或通过轻绳(杆)相连时,由于刚体和连接物轻绳(杆)均不发生形变,且轻绳(杆)的质量为零,它们不会改变系统的机械能。对整个系统而言,内部相互作用的弹力,其作用效果只是将机械能从一个物体传递给相互作用的另一个物体。由此可见,内部相互作用的弹力的瞬时功率应该总是一正一负,总和为零。又因相互作用力总是等大、反向,所以刚体或质点在弹力的方向上分速度必须相等。

根据弹力类型的不同,我们可以把速度关联问题归纳为三种模型:轻绳连接模型、轻杆连接模型和直接接触模型。对于由弹簧连接的系统,由于弹簧会储存弹性势能,不在我们讨论的范围内。

2.1 轻绳连接模型

从对速度关联问题的分析可知:由轻绳连接的物体在弹力方向上的分速度一定相等。由于轻绳上的弹力总是沿着绳的方向,就能得到两物体沿绳方向的分速度必相等,这与我们的常规处理方法是一致的。

例1:如图3所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体A和B,它们通过一根绕过定滑轮O的不可伸长的轻绳相连接,物体A以vA=20m/s匀速向右运动,在绳子与轨道成α=30°角时,则物体B的速度vB大小为多少？

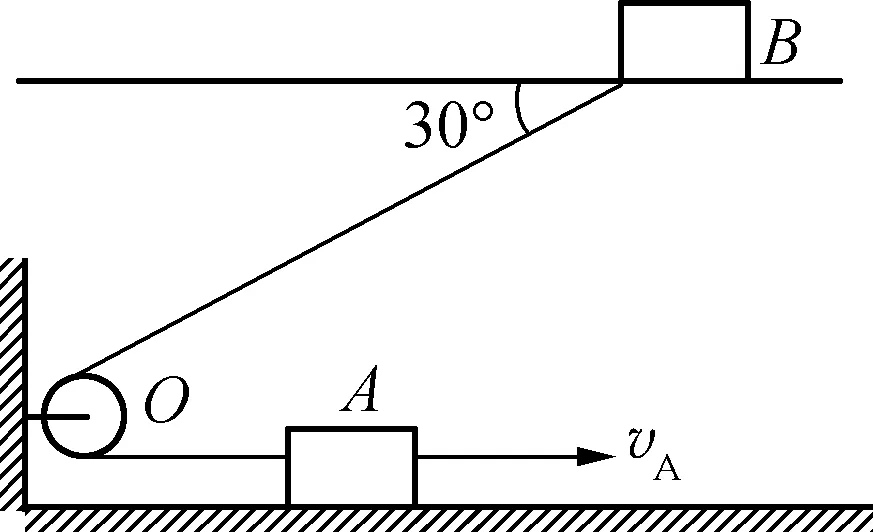
图3

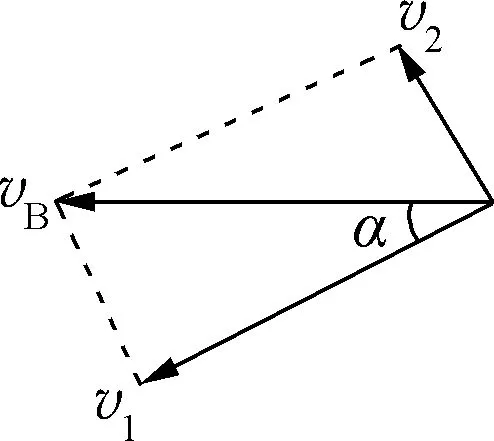
图4

解析:以物体B为研究对象,由题意可知物体B实际速度为vB,方向水平向左。将vB沿绳和垂直于绳这两个方向进行分解,得沿弹力(绳)方向上的分量v1=vBcos30°(如图4)。

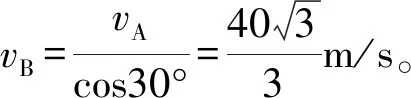
2.2 轻杆连接模型

对于轻杆连接模型,根据物体在弹力方向上的分速度相等出发,结合自由轻杆上的弹力总是沿着杆的方向,就能得到两物体沿杆方向的分速度一定相等。

例2:如图5所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点)。将其放在一个光滑球形容器中从位置1开始下滑,当轻杆到达位置2时球A与球形容器球心等高,其速度大小为vA,已知此时轻杆与水平方向成θ=30°角,B球的速度大小为vB,则( )。

B．vB=2vA

C．vB=vA

图5

图6

解析:受到球形容器制约,小球A、B绕O点做圆周运动。如图6所示，在位置2处,小球A、B的速度均沿圆的切线方向。

将小球A、B的实际速度vA、vB分别沿杆和垂直于杆的方向进行分解,则小球A沿杆方向的分速度v1=vAsinθ,小球B沿杆方向的分速度v3=vBsinθ。根据轻杆连接模型中两物体在弹力(杆)方向上的分速度相等,得v1=v3,即vA=vB,故C选项正确。

2.3 直接接触模型

在速度关联的问题中,直接接触模型是学生最难理解和掌握的。主要原因是学生无法从效果上直观判断相互关联的两个速度到底在什么方向上的分速度相等。从机械能传递的角度考察，刚体沿接触面的弹力方向上的分速度相等，抓住这个本质特征,只要正确判断出接触面上弹力的方向,问题就能得到轻松解决。

例3：如图7所示,AB绕A点以一定的角速度ω由竖直位置开始顺时针匀速旋转,并带动套在水平杆上的光滑小环运动。则小环在水平杆上运动时速度大小的变化情况是( )。

A． 保持不变

B． 一直增大

C． 一直减小

D． 先增大后减小

图7

图8

解析:杆AB与小环接触,弹力方向垂直于杆。抓住物体在弹力方向上的分速度相等的本质特征,即杆AB与小环在垂直于杆方向上速度相等。

如图8所示，选择小环作为研究对象，受水平杆约束,小环实际速度v沿水平方向。将其速度按沿杆和垂直于杆这两个方向分解,得垂直于杆方向的分量v2=vcosθ。

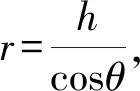
3 两个形似题的错误原因及解析

学生在处理图1、2中习题时,容易受轻杆连接模型的影响。学生的解答错误原因在于：认为物体在垂直于杆方向上的分速度相等；图2中学生的答案虽然是正确的,但也是误打误撞蒙对的。在处理这两个形似问题时,学生不考虑研究对象的选择,简单地将速度按沿杆和垂直于杆这两个方向分解来求解,没有真正找到此类问题的本质特征。其实这两个问题都属于速度关联问题中的直接接触模型，解决此类问题应牢牢抓住物体在接触面的弹力方向上分速度相等。

(1) 图1中习题解析

升降平台和直棒的末端接触,属于点面接触,弹力方向垂直于升降平面,也就是沿竖直方向。由题意可知平台实际速度为v,方向竖直向上。直杆末端的点在绕固定轴O做圆周运动,其实际速度v′的方向垂直于杆向上。

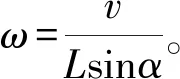
图9

图10

(2) 图2中习题解析

轻杆与物块接触,弹力方向垂直于杆。根据题意可知：物块实际速度v的方向水平向右。因为杆与物块接触的点B在绕O转动,所以B的速度垂直于杆向下。抓住杆上B点与物块在弹力方向上的分速度相等,所以与上题不同的是：本题应选择物体作为研究对象,将其速度按沿杆和垂直于杆这两个方向分解。