扩展卡尔曼滤波的安卓手机定位算法研究

袁阳,周汝雁,张云

(1. 上海海洋大学 信息学院,上海 201306;2. 农业部渔业信息重点实验室,上海 201306)

0 引 言

随着手机的广泛使用以及人们对手机的依赖程度的提高,手机定位应用的场景也越来越多,这种需求促使市场上出现了多种手机定位软件．现代生活节奏的加快,日常生活中实时获取高精度地理位置信息也成为人们不断关注的热点,例如:危险品运输车定位追踪[1],无人机配送[2]等．目前智能手机室内外定位的研究才刚起步,科研成果较少,主要原因是智能手机全球定位系统(GPS)定位模块在性能上与 GPS 接收机相差甚远[3]．任超等[4]研究了基于 GPSOne 技术的智能手机定位精度及可靠性;Zandbergen等[5]比较了辅助GPS、WiFi 和蜂窝定位技术,还研究了高灵敏度GPS手机的定位精度[6];但以上研究皆是使用辅助设备来提高手机定位精度,本文研究了利用Android手机自带的GPS芯片,通过设计扩展卡尔曼滤波定位算法来提高定位精度．

目前求解用户位置最常用的算法是加权最小二乘法．加权最小二乘法的思想就是赋予每个卫星的伪距测量值不同的权重,权重越大的伪距测量值在解方程的过程中起到的作用越大[7]． 加权最小二乘算法定位解算的步骤为: 数据准备与初值设定、线性化方程组、求解矩阵方程以及迭代性判断．加权最小二乘法不需要动态知识,仅使用伪距测量来估计位置,但该方法存在缺点:估计的质量完全取决于测量的质量,并且其要求最少的测量次数(要估计用户位置和接收机时钟偏差,通常需要4个卫星)．卡尔曼滤波技术是20世纪60年代产生的一种递推线性最小方差估计技术,估计误差最小的更多状态的估计值[8],具有以下特点[9]: 1)处理对象是随机信号; 2)被处理对象无有用和干扰之分,被处理信号通过滤波进行估算; 3)系统的白噪声激励和量测噪声并非要滤除,而是估计所需要的统计特征．GPS动态定位自适应卡尔曼滤波算法,通过仿真实验可知该方法快速有效地提高了GPS定位精度[10],滤波过程稳定[11-12]．并且扩展卡尔曼滤波在伪距差分定位[13]、多径误差削弱[14]、松组合导航[15]等应用中具有较好的效果．本文就是在扩展卡尔曼滤波算法的基础上,具体设计并实现了静态卡尔曼滤波和动态卡尔曼滤波算法,两种算法最主要的差别就是它们在状态向量和状态转移矩阵上的差别,动态卡尔曼滤波在状态向量中增加了速度参数,在低速动态实验中能够结合时间来获得更好的定位结果．

随着Android 7.0系统的发布,手机芯片提供了有关定位的应用程序接口(API),应用开发者可以根据相关API获取定位所需数据,通过使用更好的定位算法来实现更高的定位精度．本文就是通过API中提供的location类获取定位所需参数,同时使用安卓开发软件设计了静态卡尔曼滤波、动态卡尔曼滤波定位算法．鉴于手机的应用场景,本文完成了静态与低速动态实验,并与加权最小二乘法进行了对比分析,结果表明两种扩展卡尔曼滤波算法具有更好的定位效果．

1 算法描述

1.1 伪距测量

对于卫星与接收机之间伪距的测量,有如下非线性方程:

ΡRC=r+δtR-δtS+dion+dtrop+ε，

(1)

式中:ΡRC为卫星与接收机之间的伪距;r为卫星与接收机之间的几何距离;δtR为接收机钟差;δtS为卫星钟差;dion为电离层延迟;dtrop为对流层延迟;ε为接收机噪声．

如果知道接收机的近似位置,就可以将公式(1)线性化,其近似位置可以通过系统API中得到．所以在近似位置坐标处用一阶泰勒级数展开,得到如下线性方程:

ΡRC-r0+δtS-d0,ion-d0,trop，R

(2)

式中: (XS,YS,ZS)为卫星的位置坐标；(X0,Y0,Z0)为接收机的近似位置坐标．下标0表示通过使用近似接收机位置信息来估计的参数．通过该线性化伪距方程,可以得到观测矩阵．

1.2 卡尔曼滤波

1.2.1 扩展卡尔曼滤波计算过程

卡尔曼滤波算法核心思想在于:预测+测量反馈．算法将通过系统状态方程计算得到的预测值作为先验信息,之后在观测部分更新此信息．卡尔曼滤波计算过程如下:

1) 该算法在第k个历元的状态向量xk及其协方差矩阵Pk的时间预测方程为

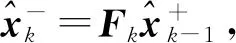
(3)

(4)

式中:Fk为状态转换矩阵;Qk为过程噪声矩阵．

2) 计算更新向量γk及其协方差矩阵Sk:

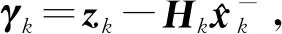
(5)

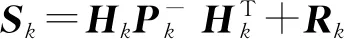
(6)

式(5)和式(6)中:zk为观测向量;Hk为观测矩阵;Rk为测量噪声协方差矩阵．

由公式(5)可以计算卡尔曼增益Kk:

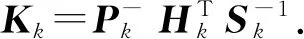
(7)

3) 由式(3)、(4)、(5)、(7)可以得到最后的测量更新方程:

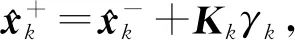
(8)

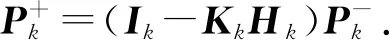
(9)

1.2.2 静态卡尔曼滤波实现

对于静态用户,本文设计的在历元k处的状态向量xk为

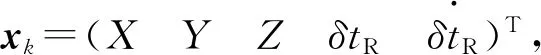
(10)

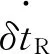
静态用户不会改变其移动位置,这意味着随着时间的推移(X,Y,Z)坐标保持不变．因此只需要考虑如何对接收器时钟的动态行为进行建模,其近似为:

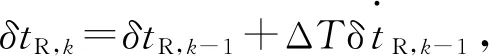
(11)

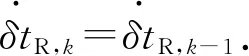
(12)

式中,ΔT是测量时间间隔．

所以就有状态转换矩阵Fk为

(13)

在静态情况下,可以假设用户没有移动并且接收器时钟具有一些频率和相位误差．因此,过程噪声矩阵Q就可以写成如下形式:

(14)

式中接收器时钟参数Sg,Sf分别表示为

Sg≈2π2h-2,

(15)

(16)

式中,h-2和h0分别为随机频率噪声和白噪声的功率谱密度(PSD)．

1.2.3 动态卡尔曼滤波实现

对于动态用户,必须考虑用户速度的问题．所以需要重新定义新的状态向量如下:

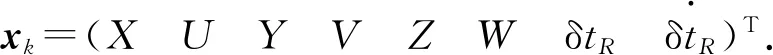
(17)

式中:U,V,W分别表示X、Y、Z方向上的速度,初始值为0．

动态卡尔曼滤波的状态向量发生改变,因此也需要重新定义一个新的状态转换矩阵Fk和一个新的过程噪声矩阵Qk,其定义如下:

(18)

式中，SX、SY和SZ分别为位置随机过程的光谱幅度,根据经验,本文中取值分别为0.5,0.5,0.1．

2 实验及设备说明

2.1 设备说明

本文实验使用的手机设备是小米6X,手机参数如表1所示.

表1 小米6X手机参数

该手机中Android版本是Android 8.1,可以通过API中提供的location类获取定位所需参数．运行内存和处理器能够保证有较好的数据收集和数据处理能力,并且支持GPS导航和北斗卫星导航系统(BDS),为实验提供了设备基础．本文算法的实现是使用GPS卫星数据．

2.2 实验说明

本文实验分为2种:静态实验和低速动态实验．

静态实验是指将手机置于某地静止不动获取数据．静态实验要求四周没有反射环境,能够很好地接收卫星信号．通过分析静态实验定位结果图像以及各个定位结果到平均值点的距离差的大小,判断每种方法在静态实验中的定位效果．

低速动态实验又分为电动车实验和步行实验．电动车实验是将手机置于电动车上行驶,步行实验是手持手机行走,两个实验都尽量保持匀速,且要求良好的实验环境．通过分析实验路线定位结果图像的变化幅度与实际路线的相似情况以及各个定位结果到实际路线的距离差,判断哪种方法更加适合动态定位．

静态实验与低速动态实验数据收集时间与平均速度如表2所示,从表中可知两个低速动态实验速度不高,是属于低速动态实验．

表2 静态实验与低速动态实验数据收集时间与平均速度

3 实验结果分析

3.1 静态实验

本文中静态实验地点是上海海洋大学信息学院旁边校友之家的楼顶,该实验环境良好,四周空旷无反射环境．实验时间为2019年5月6日中午12点20分,持续获取数据时间为半个小时．静态实验定位结果如图1所示(文中所有图片均使用Google Earth软件画出).

(蓝色:加权最小二乘法结果;红色:静态卡尔曼滤波结果;白色:动态卡尔曼滤波结果)图1 3种算法的定位结果图

由图1的定位结果可知,对于静态用户,静态卡尔曼滤波算法定位结果最集中,变化幅度最小,说明每一时刻的定位结果几乎没有发生太大变化,其定位结果最好．动态卡尔曼滤波算法定位结果相对集中,变化幅度相对较小,仅有几个数据结果较差,定位结果在旁边水面．加权最小二乘法算法定位结果变化幅度最大结果最差,有较多的数据结果定位在旁边的水面上以及草地上;其定位结果在各个方向上都有结果较差的数据．

根据计算出来的定位结果坐标,取3种方法的经纬度坐标的平均值(作为有效点),并根据坐标转换公式算出3种方法每个定位结果坐标点到有效点的距离差(单位:m),最后算出距离差的平均值,均方根值和均方根误差．其结果如表3所示:

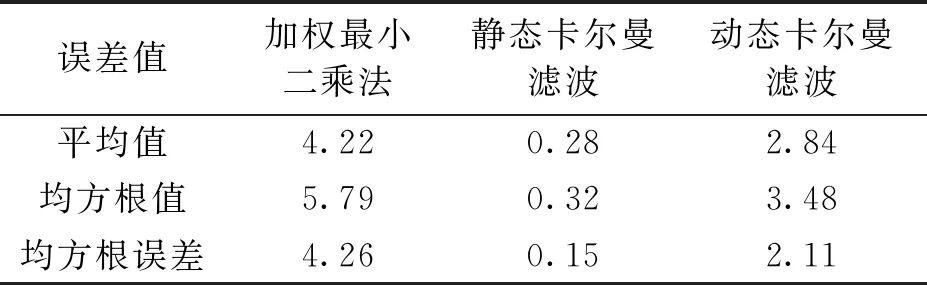
表3 3种方法距离差的平均值,均方根值和均方根误差 m

平均值越小表明通过某种算法得到的定位结果坐标越集中．均方根误差值越小,说明定位结果越好．从表3中可以看出,静态卡尔曼滤波算法得到的距离差的平均值、均方根值和均方根误差分别为0.28、0.32、0.15,其值均为其中最小,也直接说明静态卡尔曼滤波的定位结果最好．动态卡尔曼滤波算法的定位结果其次,加权最小二乘法的定位结果最差．

综上可知,静态卡尔曼滤波算法更加适合静态用户定位．

3.2 低速动态实验

3.2.1 电动车实验

电动车实验地点为：上海海洋大学体育馆旁大路,道路中间无遮蔽物,道路两旁有树木,距离道路中间有一段距离,不会有反射等情况．行走路线为直线,距离约为320 m,收集数据时间为1分30秒,电动车平均速度约为:13 km/h．3种方法的定位结果路线与实际路线如图2所示.

(蓝色:加权最小二乘法结果;红色:静态卡尔曼滤波结果;白色:动态卡尔曼滤波结果;黑色:实际路线)图2 3种方法的定位结果路线与实际路线图

图2中红色、白色、蓝色和黑色分别代表了静态卡尔曼滤波、动态卡尔曼滤波、加权最小二乘法的定位结果和实际路线．从图中可以看出,动态卡尔曼滤波和加权最小二乘法的定位结果与实际路线接近,其中动态卡尔曼滤波定位结果更加平滑,更接近实际路线,定位结果更好．静态卡尔曼滤波因为其定位结果变化幅度小,其路线明显偏离了实际路线,定位结果最差．

同步行实验数据处理相同,由于静态卡尔曼滤波方法明显偏离了实际路线,在这里不做计算．计算加权最小二乘法和动态卡尔曼滤波2种算法每个定位结果到实际行走路线的误差．它们的平均值,均方根值和均方根误差如表4所示.

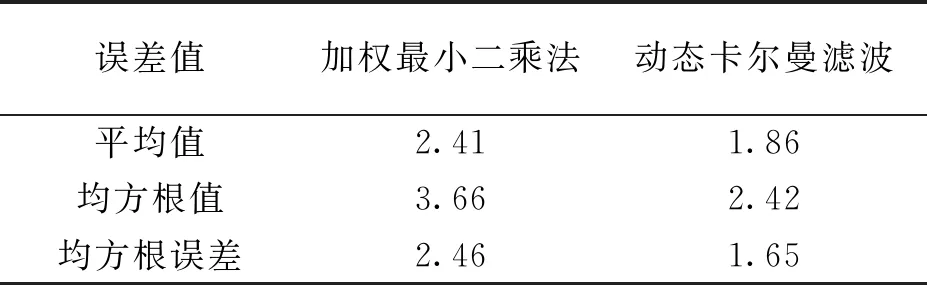
表4 2种算法误差的平均值,均方根值和均方根误差 m

从表4中可以看出,动态扩展卡尔曼滤波算法误差的平均值,均方根值和均方根误差均比加权最小二乘法的值小,表明使用该算法能够得到更好的定位结果．从该数据可知,对于电动车实验,动态扩展卡尔曼滤波定位结果最好,比加权最小二乘法更加适合低速动态实验．

3.2.2 步行实验

步行实验地点是上海海洋大学操场,该地点是一个空旷环境,周围没有反射物体．手持手机收集数据,行走路线为外圈椭圆形,速度约为5.4 km/h,收集数据时间为5分40秒． 其定位结果如图3所示.

(蓝色:加权最小二乘法结果；红色：静态卡尔曼滤波结果;白色:动态卡尔曼滤波结果)图3 步行实验结果

图3中,红色、白色和蓝色分别代表了静态卡尔曼滤波、动态卡尔曼滤波和加权最小二乘法的定位结果．行走路线为操场最外圈、接近红白相间处的椭圆形,由于实际路线没有具体坐标数据,所以并未在图中画出,也无法计算两种方法距离行走路线误差的平均值,均方根值和均方根误差．从图中可知,加权最小二乘法和动态卡尔曼滤波最接近实际行走路线,适合动态用户定位．但其中动态卡尔曼滤波路线波动幅度较小,可以看出其误差更小．而静态卡尔曼滤波结果同电动车实验相同,定位结果变化幅度小,与实际路线明显偏差较大,说明静态卡尔曼滤波不适合动态用户．从静态卡尔曼滤波的推导公式中也可以看出,在它的状态向量、转换矩阵中没有速度的概念,不能令其定位结果随时间变化而快速改变．

从电动车实验和步行实验结果可知:动态卡尔曼滤波算法更加适合低速动态实验．

4 结束语

针对现阶段直接利用手机的GPS芯片原始数据的定位研究比较少的背景,本文主要对基于手机GPS原始数据定位可行性以及定位算法进行了研究．利用Android 7.0系统提供的API获取定位所需GPS原始数据参数,并将这些参数应用到设计的静态卡尔曼滤波和动态卡尔曼滤波算法中．为测试算法的性能,进行了静态实验和满足日常手机定位需要的低速动态实验,并与传统的加权最小二乘法作对比分析．在分别进行的静态实验以及电动车实验和步行实验的实验结果可以看出:在静态实验中,静态卡尔曼滤波误差的平均值和均方根误差值都是最小,其定位结果最好．在低速动态实验中,动态卡尔曼滤波误差的平均值和均方根误差值都是最小,定位结果最好,更加接近实际路线．

实验结果证明了利用手机GPS原始数据实现定位的可行性,同时也证明了本文设计的卡尔曼滤波算法可以提高相应场景的定位精度,论文的研究结果为将来实现静态与动态的高精度手机定位算法(如RTK算法)提供了必要的理论依据．