基于EMD-LSTM耦合预测模型的BDS多路径误差削弱方法研究

徐小汶,陶 远

(安徽理工大学 测绘学院,安徽 淮南 232001)

0 引 言

在北斗卫星导航系统(BDS)高精度变形监测中,通常采用相对定位的方式观测. 其中,虽然采用双差法可以完全消除卫星钟差与接收机钟差,也可凭借短基线测量中测站间距离较短的原因忽略电离层延迟与对流层延迟的影响,但多路径误差却不能通过差分法消除,在BDS观测数据中依然存在[1]. 因此,多路径误差成为高精度BDS应用的主要误差源.

除合理的选址可降低多路径误差的影响外,削弱多路径误差的方法主要集中在接收机硬件和数据后处理两方面. 从硬件方面削弱多路径误差,主要通过改进接收机天线的方式来抑制多路径误差,但其存在成本较高且消弱多路径误差效果较差的问题. 鉴于此,众多学者采用数据后处理的方式削弱多路径误差,展开了一系列的研究. 其中应用最为广泛的理论有如下几种:基于信噪比方法或载噪比对全球定位系统(GPS)观测值进行多路径误差削弱[2-3];基于多种滤波技术消除多路径误差,如基于交叉认证技术的Vondrak滤波[4]、经验模态分解(EMD)方法[5-6]、小波分析[7]等. 虽然上述理论的研究取得了良好的效果,但上述后处理方法均是基于恒星日滤波技术进行应用. 而BDS具有星座异构的特点,其MEO卫星的回归周期与地球静止轨道(GEO)卫星、倾斜地球同步轨道(IGSO)卫星相差较大,因此在坐标值域中恒星日滤波方法将难以适用.

鉴于坐标值域序列优秀的后处理效率,同时针对BDS坐标值域中多路径误差难以适用恒星日滤波方法[7-8]以及神经网络预测结果存在滞后性的问题,本文在深度学习方法的基础上,提出采用EMD-LSTM的多路径误差预测模型进行多路径误差剔除. 本文的研究内容如下:首先基于EMD算法对多路径误差进行多尺度分解,然后利用长短期记忆神经网络(LSTM)对模态分量进行建模预测,最终将预测值重构多路径误差,以此构建多路径误差的预测模型,实现多路径误差的准确改正.

1 多路径误差原理

在BDS测量中,卫星信号被测站周围的障碍物影响,产生了反射或衍射现象. 这些干扰信号影响直射信号,从而使观测值产生偏差或失真,这些干扰信号比直接信号有着更长的传播路径,导致产生传播延迟,这种由多路径的信号传播所引起的干涉时延效应被称作多路径效应,这种效应导致的误差为多路径误差. 多路径误差是BDS测量中一个重要的误差源,多路径误差将严重损害BDS测量的精度,甚至将产生信号的失锁[9].

由于多路径误差信号属于载波信号,所以多路径误差具备与载波信号相同的性质,因此反射信号造成的多路径误差可简单表示为

Sr=αAcos(φ+θ), 0≤α≤1，

(1)

式中:A与φ为反射信号的振幅与相位;α为反射因子；θ为多路径误差延迟相位. 多路径误差造成的相位误差可表示为[10]

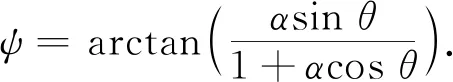
(2)

对于L1载波,多路径误差可使定位结果出现最大约4.8 cm的误差.

对于短基线相对定位,多路径误差与测站环境、观测卫星与接收机有关,当周围环境变化较小或保持静止时,每个运行周期为一个恒星日的卫星到接收机天线的几何关系是相同的. BDS星座异构,坐标值域序列无固定周日重复性,难以对坐标值域进行恒星日滤波.

2 EMD-LSTM耦合模型

2.1 EMD原理

在处理BDS多路径效应问题时,通常选择对观测数据进行降噪,以便最大程度上消弱多路径误差的影响. 本文选择由Huang等[11]提出的经验模态分解方法,也称EMD算法. EMD算法的思想是:将BDS观测数据看成是由一些互异的非正弦函数的信号分量构成. 依据这一特性,可以将复杂且波动较大的BDS观测数据分解成若干个信号分量,并由高频到低频依次排列,这些信号分量称为固有模态函数(IMF)[11-12].

针对BDS原始观测序列x(t)的多尺度分解可以表示为

(3)

式中:imfi(t)为第i个多尺度分量;rn(t)为残差余项.

EMD算法的实施步骤描述如下:

1)判断BDS原始观测数据x(t)中局部的极值点;

2)通过三次样条插值函数获得步骤1)中的局部极值点,并以此为基准构建观测数据x(t)的上、下包络线xu(t)和xd(t));

3)计算步骤2)中得到的xu(t)和xd(t)的平均值,其计算公式为

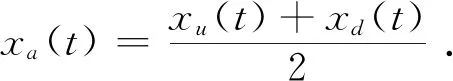
(4)

4)判断q(t)是否满足均值条件

q(t)=x(t)-xa(t).

(5)

若q(t)为零,此时可认为满足要求并继续进行运算;否则重复步骤1)～4),直至q(t)满足均值条件;

5)提取BDS观测数据中的残余项ri(t),并判断ri(t)是否满足余项条件:

ri(t)=x(t)-imfi(t).

(6)

若极值点数ri(t)< 2,满足余项条件,分解完成;若ri(t)> 2,则继续按照上述步骤进行分解.

关于降噪问题的尺度选择问题,常用的方法有以下几种:①累积偏差法;②交叉认证法;③去除第一个IMF分量法;④依据通过分解后的IMF分量的能量密度与平均周期的乘积为常数值的特性,所设计的尺度选择方法. 依据上述方法的便捷性与理论的严密性,本文选择④中张敬霞[13]提出的一种自适应选择IMF分量的算法,具体描述如下:

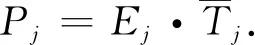
(7)

(8)

(9)

式中:Aj和Qj分别为第j个IMF分量的振幅和极值点的总和;n为每个IMF分量的长度.

2)计算RPj系数:

(10)

若RPj≥1,即认为所计算出的前j-1个IMF分量Pj为常数,将第j个IMF分量视为重构信号的尺度.

2.2 LSTM原理

长短期记忆网络(LSTM)是Hochreiter和Schmidhuber在1997年所提出的一种特殊的深度学习方法,能够很好地解决梯度爆炸和梯度消失问题,让循环神经网络具备更强更好的记忆性能. LSTM是使用独特的“门”结构构建的,一般包括三个基本组件,分别是“忘记”,“输入”和“输出”门,三个组件协同工作以完成LSTM单元的功能并控制信息流[14].

在“忘记”门中,采用S型函数σ(*)记录前一个状态单元的储存信息,表达公式如下[15]:

ft=σ(Wf[ht-1,xt]+bf),

(11)

式中:σ(*)为S形函数;Wf和bf为训练后要确定的参数;ht-1为时间段t-1的隐藏状态,xt为时间段t的输入向量,ft为S型函数的输出量.

函数的输入量是前一个LSTM单元和输入向量的隐藏状态. 因此,函数的输出量是介于0到1之间的值,并与前LSTM单元在单元状态下的每个数字相对应. 这些值表示在先前单元状态Ct-1中每个数字的遗忘度. 值“1”表示“完全保留”,相反,值“0”则表示“完全忘记或排除”[16].

it=σ(Wi[ht-1,xt]+bi),

(12)

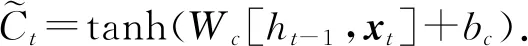
(13)

式中:σ(*)为S形函数;Wi,bi,Wc和bc为参数,将通过训练过程确定,h为时刻t-1的隐藏状态；xt是输入向量.

最后,使用“输出”门来决定和控制输出. 此“门”由S型函数和tanh函数组成,表达公式详见式(14)和(15). 其中,sigmoid函数的输出量为Ot,它确定隐藏函数的输出状态,同时将单元状态通过tanh函数并乘以向量Ot,用于确定LSTM单位的输出.

Ot=σ(Wo[ht-1,xt]+bo),

(14)

ht=Ot*tanh(Ct).

(15)

式中:Wo和bo为训练期间确定的参数;Ct为t时刻的细胞状态.

2.3 EMD-LSTM的BDS多路径误差建模

在实验中发现BDS多路径误差呈现高度非线性特征,且具有非平稳时间序列的特性.若将多路径误差分解为多模态分量,其各分量的非线性程度不但能够降低,时间序列还会变得更加平稳,利于采用LSTM模型进行预测. 本文将EMD算法和LSTM方法相结合,构建一种基于EMD-LSTM耦合预测模型,对BDS坐标序列中的多路径误差进行预测,当获取到对应历元的数据时,对应改正其多路径误差.

基于EMD-LSTM耦合预测模型的流程图如图1所示,其削弱BDS多路径效应的具体实施步骤如下:

1)对训练数据多路径误差x(t)进行多尺度分解,分解成若干IMF分量;

2)根据式(10)计算RP系数,自适应舍弃高频的噪声IMF;

3)分别对有用信息的IMF分量进行LSTM预测;

4)预测分量重构多路径误差x′(t),改正实测序列.

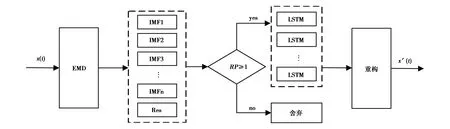
图1 EMD-LSTM耦合模型流程图

3 实验与结果

3.1 数据来源

本实验数据采集于安徽理工大学测绘学院五楼楼顶,由两台相同的接收机于2018-05-13-2018-05-15(共3天数据,年积日分别为DOY133、DOY134和DOY135)同时段接收BDS数据,采样频率为1 Hz,卫星截止高度角15°,接收机参数为天宝BD980板卡,AT300天线,支持BDS双频,且接收机采用扼流圈天线. 接收机间距离约为12 m,由于接收机距离较近,高程方向基本相当,可忽略对流层延迟、电离层延迟影响,并且天线相位中心偏差较小且稳定,因此测量型天线相位偏差对本文分析内容影响可忽略不计,但多路径误差在站星间差分无法削弱,综上所述,原始观测序列中仅存在多路径误差和噪声.

原始观测数据使用goGPS软件( https://sourceforge.net/projects/gogps/),使用最小二乘方法的单历元解算基线,基于站心坐标系下得到基线的E、N、U方向分量.

3.2 实验方案

为了更好展现耦合模型的预测性能,设置如下方案进行对比:

方案一:EMD-LSTM耦合模型;

方案二:EMD方法降噪后直接以LSTM网络预测实验.

为了比较建模方法的预测结果,采用平均百分比误差(MAPE)和均方根误差(RMSE),两个指标来衡量模型的预测结果,数值越小,模型精度高,则说明预测效果好.

MAPE计算公式为:

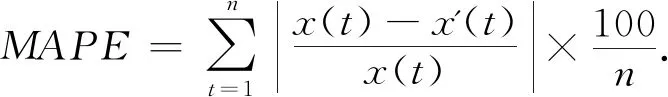
(16)

MAPE值反映的是同组数据的不同网络训练出的模型优劣情况,与训练样本大小无关,MAPE值仅可评价同组数据在不同模型下的效果,不同训练数据下的指标大小无法进行评价.

RMSE计算公式为

(17)

3.3 BDS实验结果分析

对当天进行预测时,首先取前一天原始观测数据为训练数据,该天数据为测试数据,若对DOY134进行预测时,需取DOY133为训练数据,其中原始观测数据如图2所示. LSTM网络迭代次数为100次,输入变量数为100历元,输出变量数为1历元,时间步长设置为256,隐含层为12. 为了减小建模误差,在进行训练前将数据进行归一化处理,预测后进行反归一化即得真实预测值.

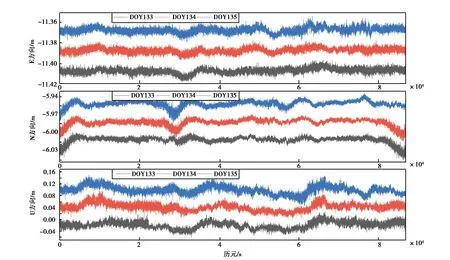
图2 三天的原始坐标序列

为方便观测坐标序列趋势,在DOY134和DOY135各方向添加一定数值. 接收机虽装有扼流圈天线,由图2所示,多路径误差依然明显,同时证明了硬件端削弱多路径误差程度有限. 限于篇幅,仅以E方向为例. 首先将训练数据进行EMD多尺度分解,图3为DOY133的E方向坐标序列经EMD分解的模态分量图.

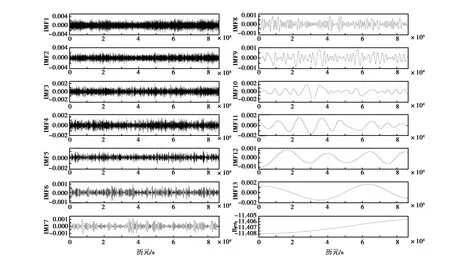
图3 DOY133的E方向坐标序列EMD分解结果

分解得13个模态分量与1个残余分量,计算分解提取尺度的RP系数在IMF4开始RP大于等于1,IMF1到IMF3均为高频的随机噪声并剔除. 对IMF4至IMF13和Res分别进入LSTM网络训练和预测,并对预测得到的分量重构多路径误差. 图4为两组方案的预测结果.

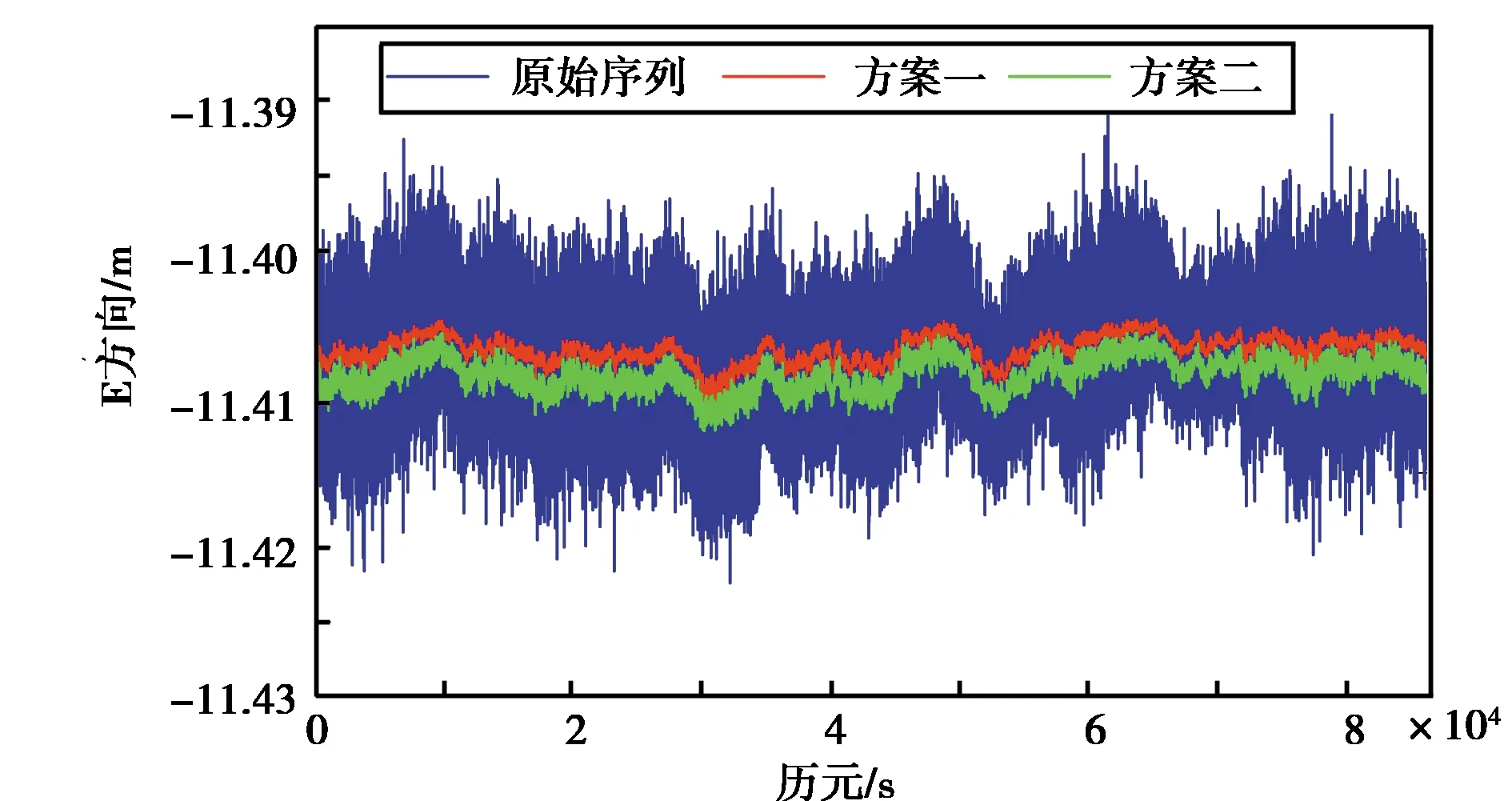
图4 两种方案的预测结果

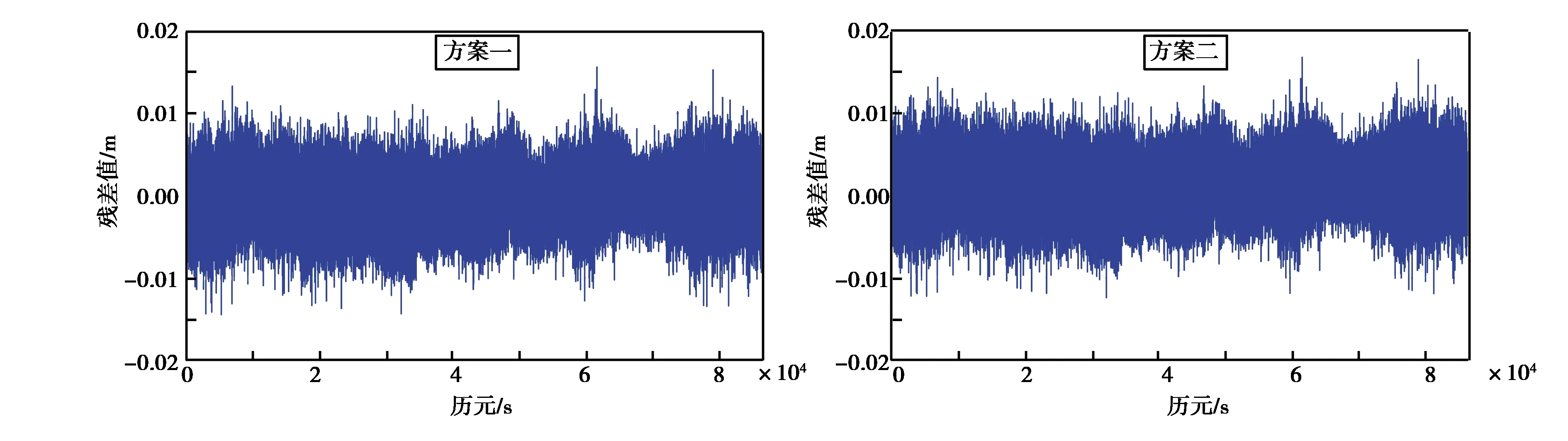
图5 两种方案消除多路径误差的坐标序列

如图4～5所示,两种方案的预测结果虽在趋势上具有一致性,但二者明显存在偏移.其中,两种方案得到的残差序列,均呈现正态分布,方案二的残差序列明显存在滞后性,即并不在0处波动,这也满足深度学习方法在预测中存在的滞后性特点,但基于EMD-LSTM耦合预测模型较好的解决了这一问题. EMD-LSTM方法能够将非线性、非平稳性序列良好的学习序列的深层规律. 由表1所示,EMD-LSTM耦合模型的RMSE和MAPE值均比方案二略优,但方案二的均值较大,即后者在改正多路径误差时,有用信息被误处理.

由表2所示,EMD-LSTM耦合方法能够有效的削弱多路径误差,其中对U方向精度改善程度达到了40.30%、41.00%,对E、N方向改善程度分别为24.91%、22.93%和36.84%、39.07%.

表1 两种方案消除多路径误差的坐标序列指标对比

表2 EMD-LSTM耦合模型消除多路径误差前后的RMSE对比

4 结 论

在BDS坐标值域中,因星座异构特性,恒星日滤波方法难以适用. 本文引入EMD-LSTM耦合预测模型,对多路径误差进行预测建模并改正,得出以下结论:1)本文设置的两组方案,且均得到较好的结果,但EMD-LSTM耦合方法改善了深度学习方法预测中存在的滞后性问题,提高了多路径误差改善程度;2)EMD-LSTM耦合预测模型能有效地削弱多路径误差影响,坐标值域中的多路径误差改正不再局限于恒星日滤波方法,对E、N、U方向精度改善明显. 从本文的研究可以看出,基于深度学习方法的多路径误差剔除,在测量数据处理中有着广阔的应用前景,后期需要解决深度学习在实时多路径误差剔除中的应用问题.