eLoran系统新型信号波形设计及其性能评估

李婉清, 刘中伟, 李实锋, 叶清琳

(1.中山大学 电子与通信工程学院，广东 广州 510006;2.国防科技大学 信息通信学院,陕西 西安 710106;3.中国科学院国家授时中心,陕西 西安 710600;4.中国交通信息科技集团有限公司,北京 100011)

0 引 言

定位导航授时(PNT)系统为世界各地的军事、商业和民用用户提供全空域目标定位、导航与授时服务,是国家经济和安全依赖的基础设施[1]．陆基远程导航系统与全球卫星导航系统(GNSS)在工作体制、工作频率以及信号强度等方面具有互补性,是GNSS的有效备份[2]．罗兰(Loran)系统、长河二号等是典型的提供区域覆盖的陆基远程无线电导航系统．

由于GNSS具有单一性与脆弱性,包括荷兰、美国、英国以及韩国等都认识到GNSS备份系统建立的重要性,并开展了增强型罗兰(eLoran)系统的研究[3-4]．

我国自主的陆基远程无线电导航系统研究与建设始于20世纪60年代,与国际陆基无线电导航系统概念的研究同步进行．2008年,中国科学院国家授时中心完成了BPL长波授时系统现代化技术升级改造,使其具备eLoran信号发射的基本条件[5]．与此同时,长河二号导航系统完成现代化技术升级,实现导航、授时一体化,且经过改造的长河二号系统也具备了eLoran信号发射的基本条件．在完善我国北斗卫星导航系统(BDS)的同时还需要大力发展其备份系统(如BPL长波授时系统、长河二号导航系统),形成完备、多源的国家综合PNT体系,保障国家安全与国民PNT服务实现提升[6]．

随着我国eLoran授时台增补完善,我国eLoran导航系统已基本实现信号全国土覆盖．随着传播距离缩短,信号干扰(如天波延迟)将相应减小,信号在时域方面产生较大冗余．加速波形后沿下降将有益于减小信号间的交叉干扰,缩短波形持续时间可用于增加信号、加载更多数据．

标准Loran C信号的前65 μs有严格定义,而后一部分未有定义[7]．利用波形后沿部分的改进,完善eLoran系统信号体制,可提高接收性能,比如美国UrsaNav机构研究发现eLoran系统短脉冲波形并不会削弱导航性能．本文在标准Loran C信号的基础上,参考短脉冲试验波形进一步研究新型脉冲信号波形,并对其频谱特性[8]进行评估．相关的实验结果可为eLoran系统新型的调制方式提供理论参考．

1 eLoran原有信号体制

eLoran导航系统发射信号的工作频段是90～110 kHz．eLoran单脉冲信号为标准Loran波形(Chayka波形),载波中心频率为100 kHz,是一种相位调制脉冲．标准Loran C信号的数学模型严格定义为

s=

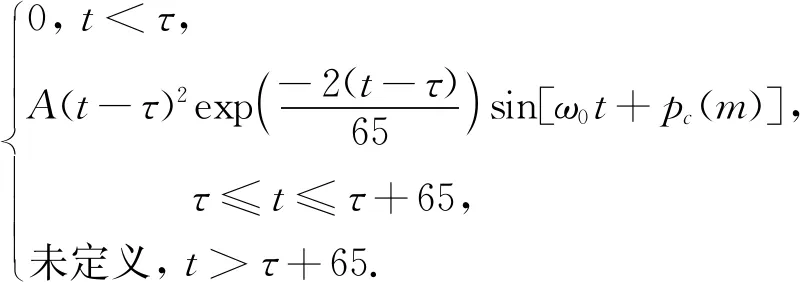
(1)

式中:A为与峰值电流有关的常数;t为时间,单位μs;τ为包周差,单位μs;ω0为载波频率,取值为0.2 πrad/μs;pc(m)为相位编码,取值0或π．

在理想情况下,取τ=0,pc(m)=0,A=1,标准Loran波形如图1所示．

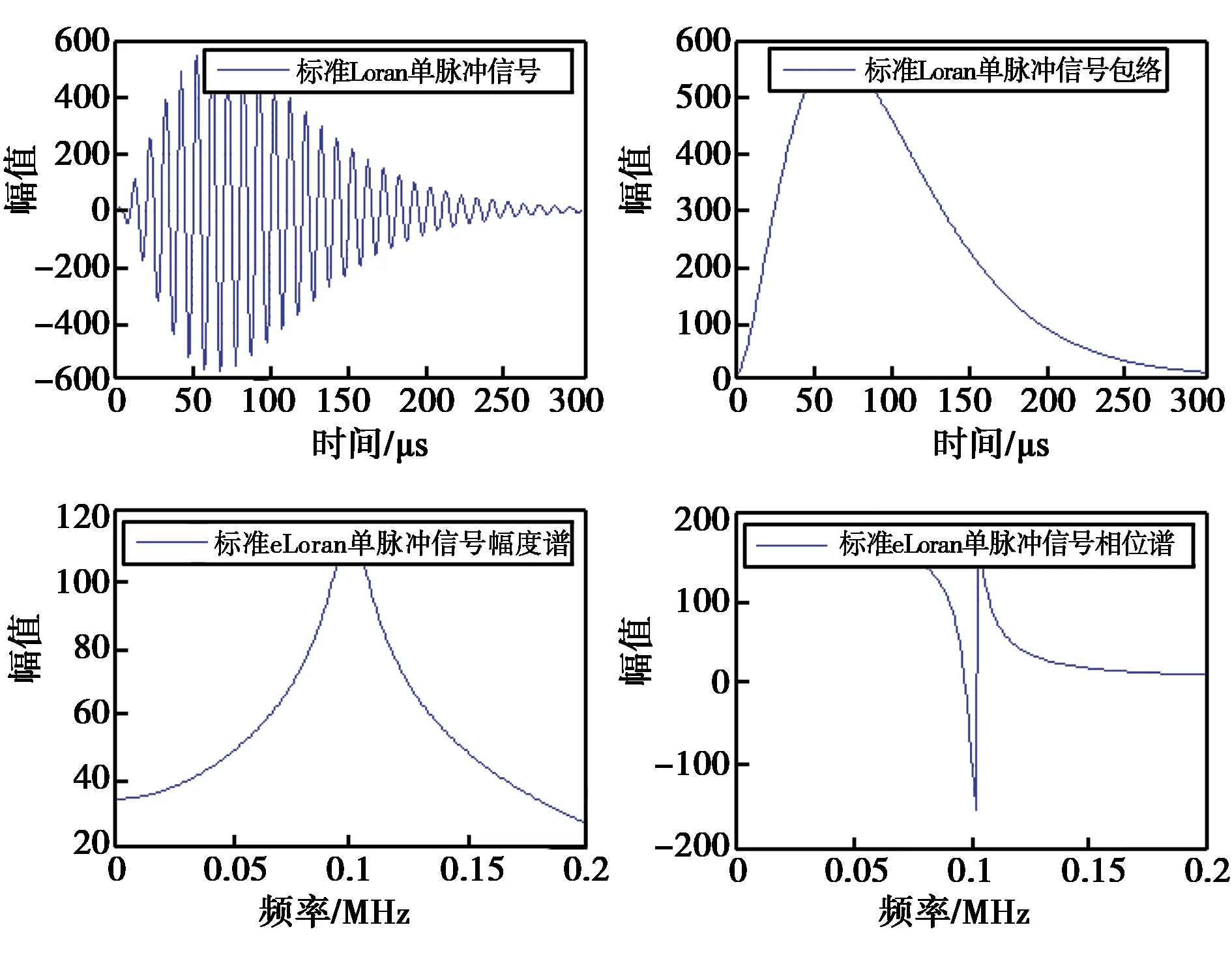
图1 标准Loran脉冲信号波形图

标准Loran C信号前沿快速上升而后沿下降缓慢,这使得信号能量能够集中在工作频段内．信号频谱特性如图2～3所示,信号的3 dB带宽约为0.7 kHz,信号频谱衰减20 dB的带宽约为90～110 kHz．标准Loran C信号时域波形持续时间约260 μs,信号能量也集中在该时段中．尽管标准Loran C信号对波形的前沿阶段有严格要求,对于后沿脉冲幅度却未有严格定义．实现脉冲后沿加速下降,可以减小脉冲信号间交叉干扰与天波干扰,可增加脉冲数量、调制更多信息．所以,改变后沿脉冲持续时间与幅度变化可作为新型波形设计的两大基本思路．

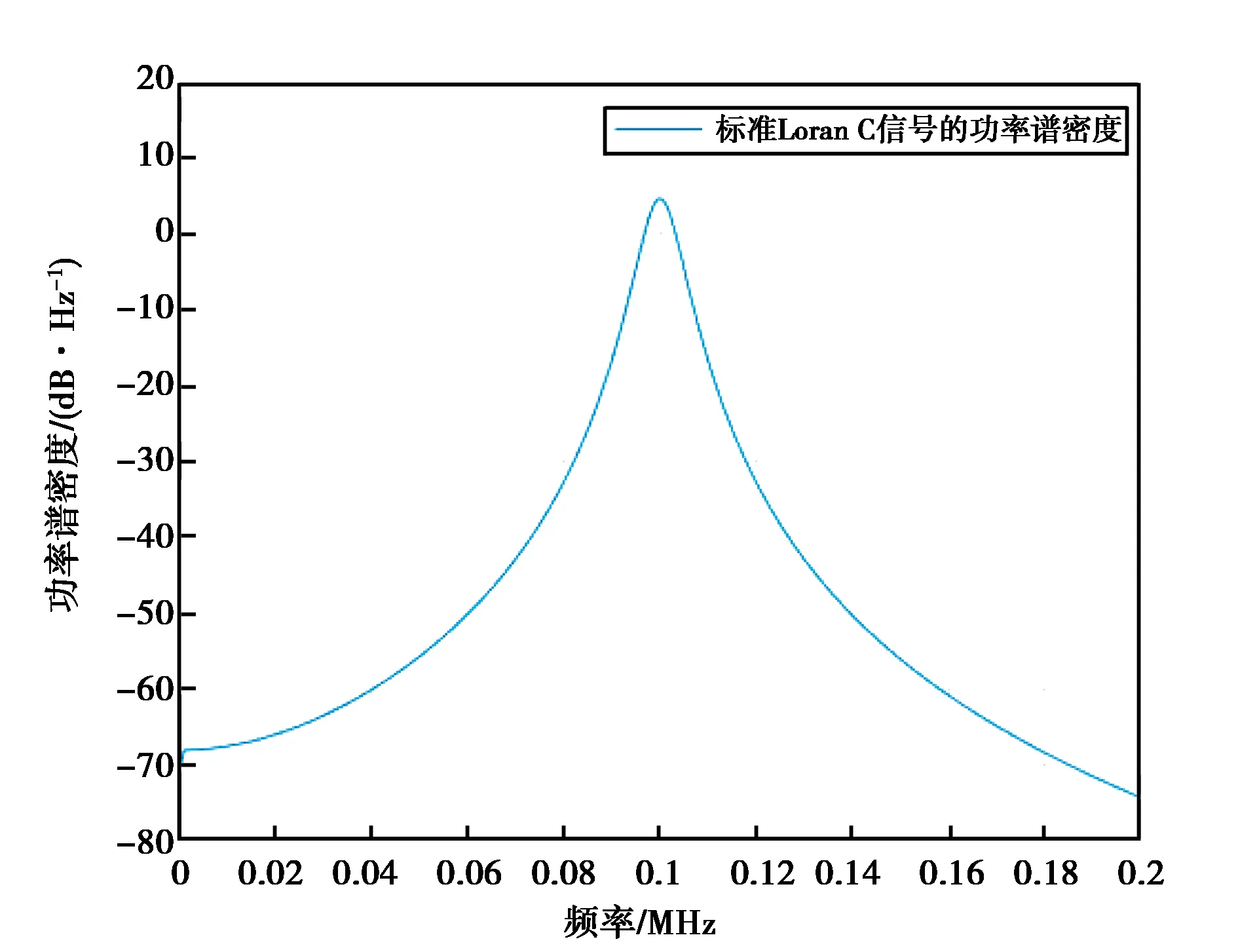
图2 标准Loran C脉冲信号功率谱密度图

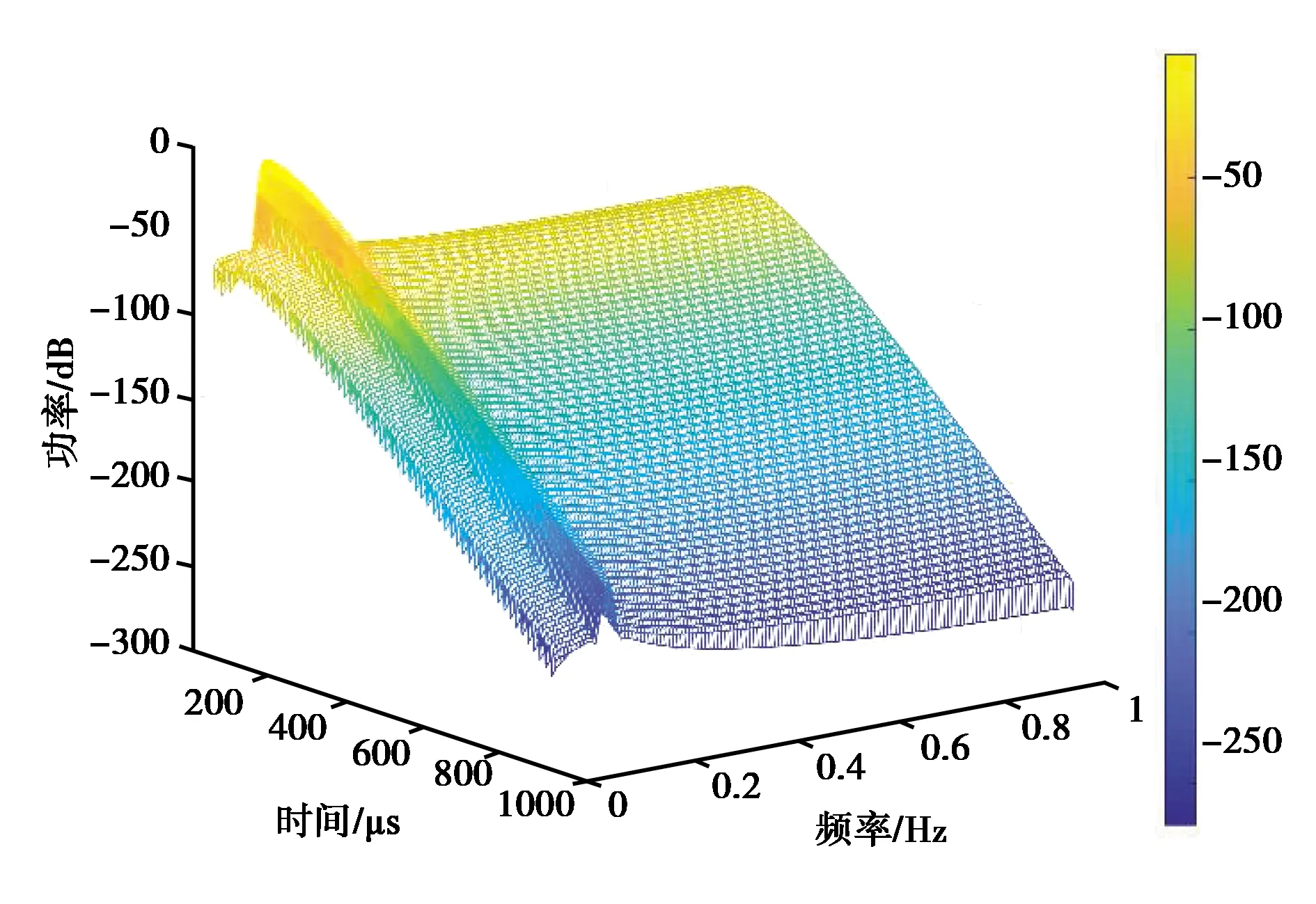
图3 标准Loran C脉冲信号时频分析三维图

2 eLoran信号新型波形设计

目前eLoran信号波形中仅前65 μs波形有严格定义,而就目前常用的调制方式来说,数据传输的有效性较低．为进一步实现数据传输量的增加与传输功耗的降低,本文对65 μs后波形进行优化处理,主要设计思路是:

1) 保持前沿不变,幅度不变;

2) 加速后沿下降;

3) 缩短脉冲波形持续时间．

本文采用采样频率2 000 kHz进行性能仿真分析,仿真信号时域长度均为800 μs．

2.1 衰减函数法

新型脉冲的前65 μs波形与标准Loran信号波形相同,对65 μs后波形进行重新定义,利用衰减函数加速原波形后沿下降,定义为

s=

(2)

式中:damp-function(t)为衰减函数．考虑三种常用的衰减函数,即指数衰减函数、高斯衰减函数、线性衰减函数．

2.1.1 指数衰减

首先,考虑指数衰减,可将指数衰减函数定义为:

(3)

式中:num-damp为控制后沿下降速度的常数．取A=1,τ=0,pc(m)=0,下同．图4为num-damp=130所形成的新型脉冲波形与标准Loran脉冲波形的对比示意图．

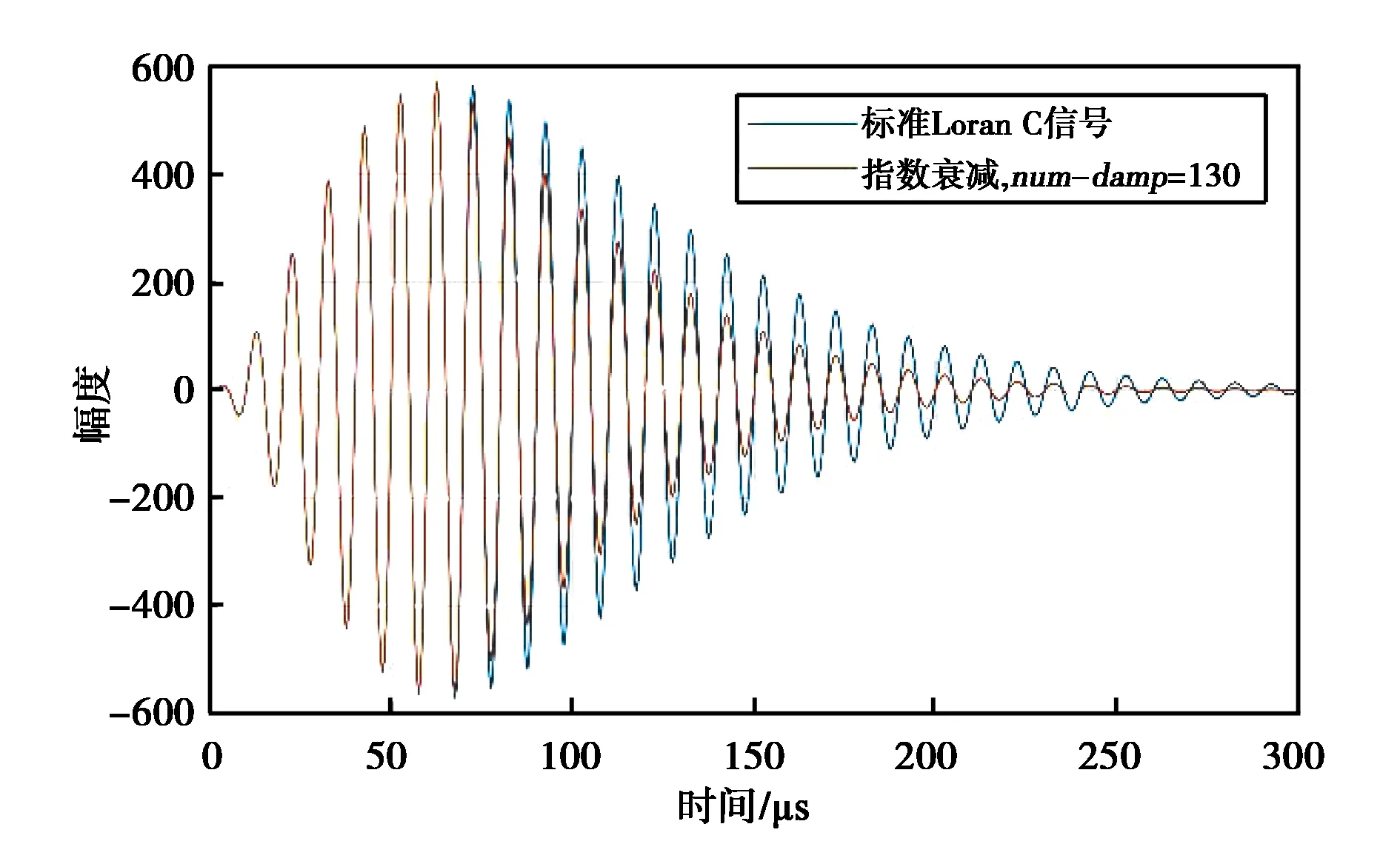
图4 标准脉冲波形与指数衰减加速后沿下降新型Loran C波形示意图

2.1.2 高斯衰减

其次考虑高斯衰减,可将高斯衰减函数定义为

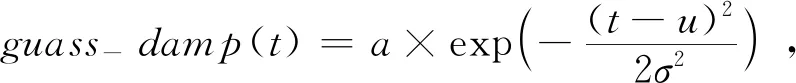
(4)

式中:a为高斯函数曲线的峰值,这里取a=1,以达到平滑衰减的效果;u为位置参数,这里取65;σ(图5中记为sigma)为尺度参数,为高斯函数的均方根(RMS)宽值．图5为取σ=60的新型脉冲波形与标准Loran C脉冲波形的对比示意图．

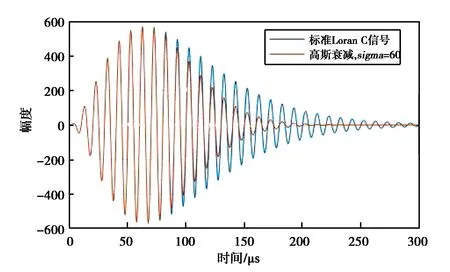
图5 标准脉冲波形与高斯衰减加速后沿下降新型Loran C波形示意图

2.1.3 线性衰减

由于线性衰减函数系数衰减到零后为负数将造成波形反向,所以在线性函数横轴过零点处将进行截断,重新定义线性衰减函数的新型波形如下:

s=

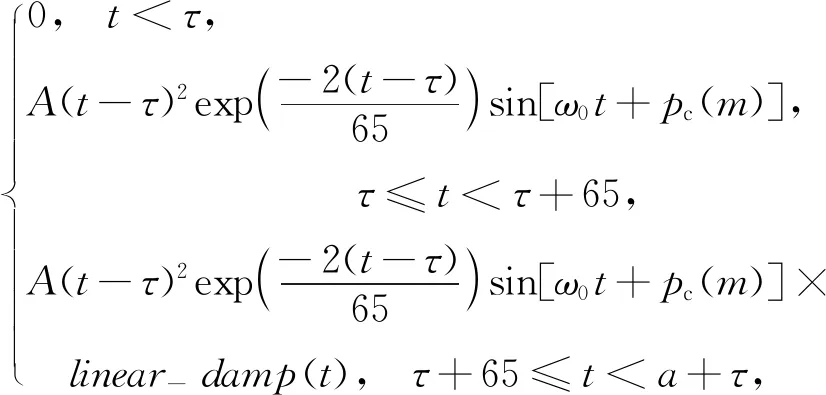
(5)

(6)

式中:a、b分别为线性函数的横、纵轴截距．为实现后沿波形平滑下降,b受a约束．图6～8示出a=200时,线性衰减函数的后沿波形加速下降效果与标准Loran C信号波形对比．

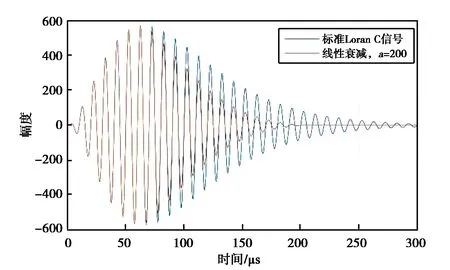
图6 标准脉冲波形与线性衰减加速后沿下降新型Loran C波形示意图

以上三种衰减函数效果如下:

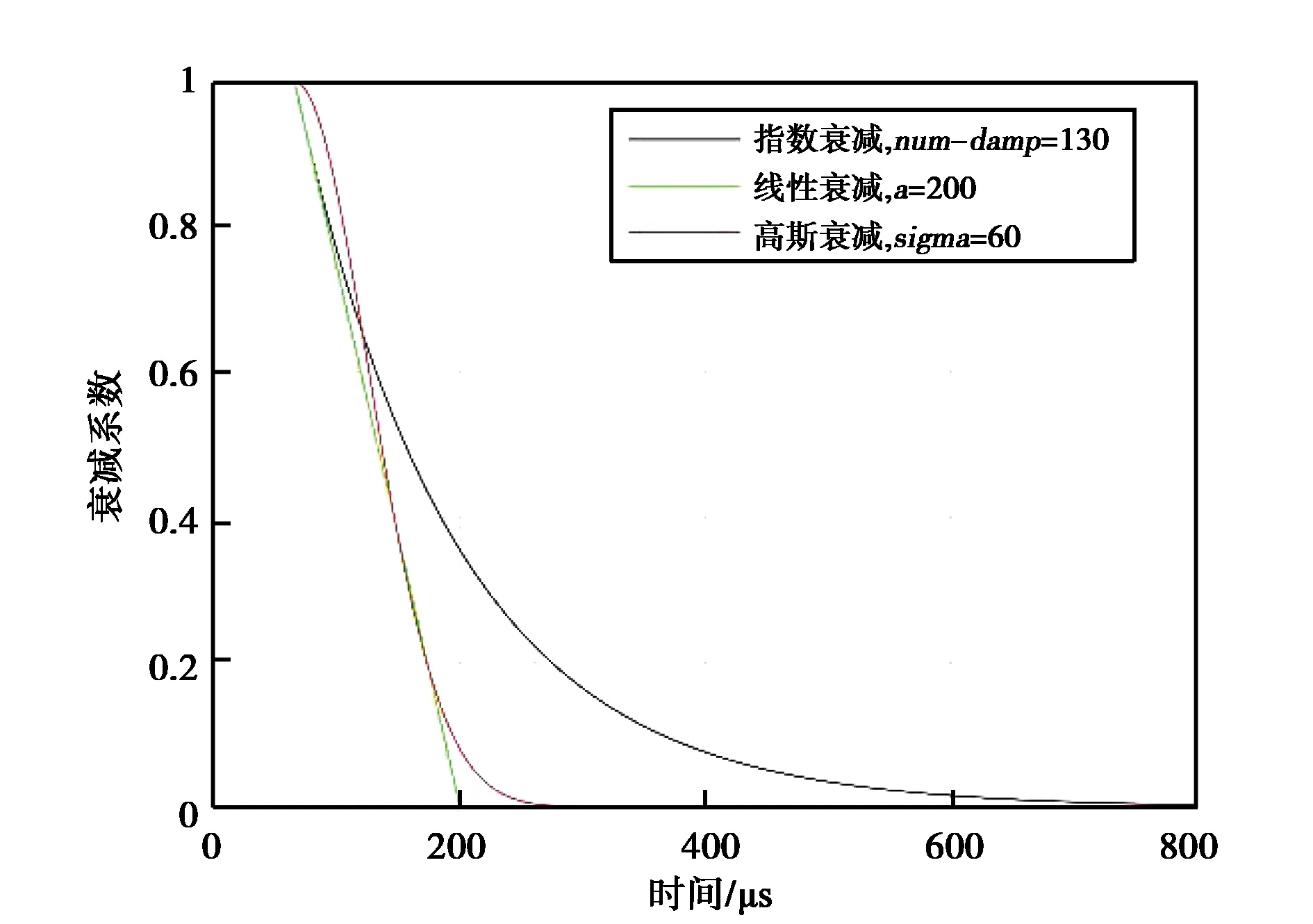
图7 三种衰减函数衰减效果示意图

图8 三种衰减波形与标准Loran C信号波形比较示意图

在选择图8所标记的仿真参数下,高斯衰减与线性衰减速度要比指数衰减更快,高斯衰减与指数衰减的区别在于高斯衰减前一部分的衰减速度较慢,而后一部分衰减迅速,这样能够保证功率谱实现较平滑的衰变．指数衰减后沿形成较长拖尾,易对后一脉冲信号造成干扰．

2.2 对称波形法

对称波形基本设计思想是利用标准Loran波形的前65 μs作为后沿波形并形成对称,该新型波形设计方法能够将波形持续时间缩短到100 μs左右．

2.2.1 中心对称

在标准Loran信号的前65 μs波形基础上,加上与前65 μs相同的波形,定义为

s=

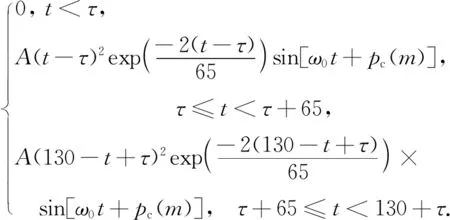
(7)

式中:A为与峰值电流有关的常数;t为时间,单位μs;τ为包周差,单位μs;ω0为载波频率,取值0.2 π rad/μs;pc(m)为相位编码,取值0或π．

取A=1,τ=0,pc(m)=0．图9为形成的新型脉冲波形与标准Loran C脉冲波形的对比示意图．

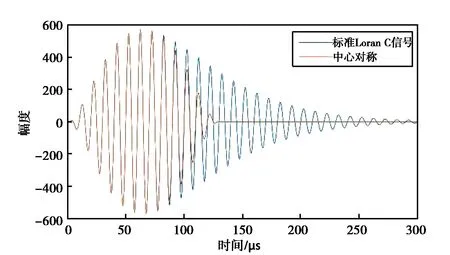
图9 中心对称波形与标准Loran C信号波形比较示意图

2.2.2 过渡对称

前65 μs与标准Loran波形相同,中间为了相位衔接,加不同长度(5 μs的奇数倍)的正弦波,之后再加65 μs与前65 μs对称的波形．定义为

s=

(8)

式中:A为与峰值电流有关的常数;t为时间,单位μs;τ为包周差,单位μs;ω0为载波频率,取值0.2 π rad/μs;pc(m)为相位编码,取值0或π;tp为中间加的正弦波,取值5 μs的奇数倍．

取A=1,τ=0,pc(m)=0．图10为tp=35 μs所形成的新型脉冲波形与标准Loran C脉冲波形的对比示意图．

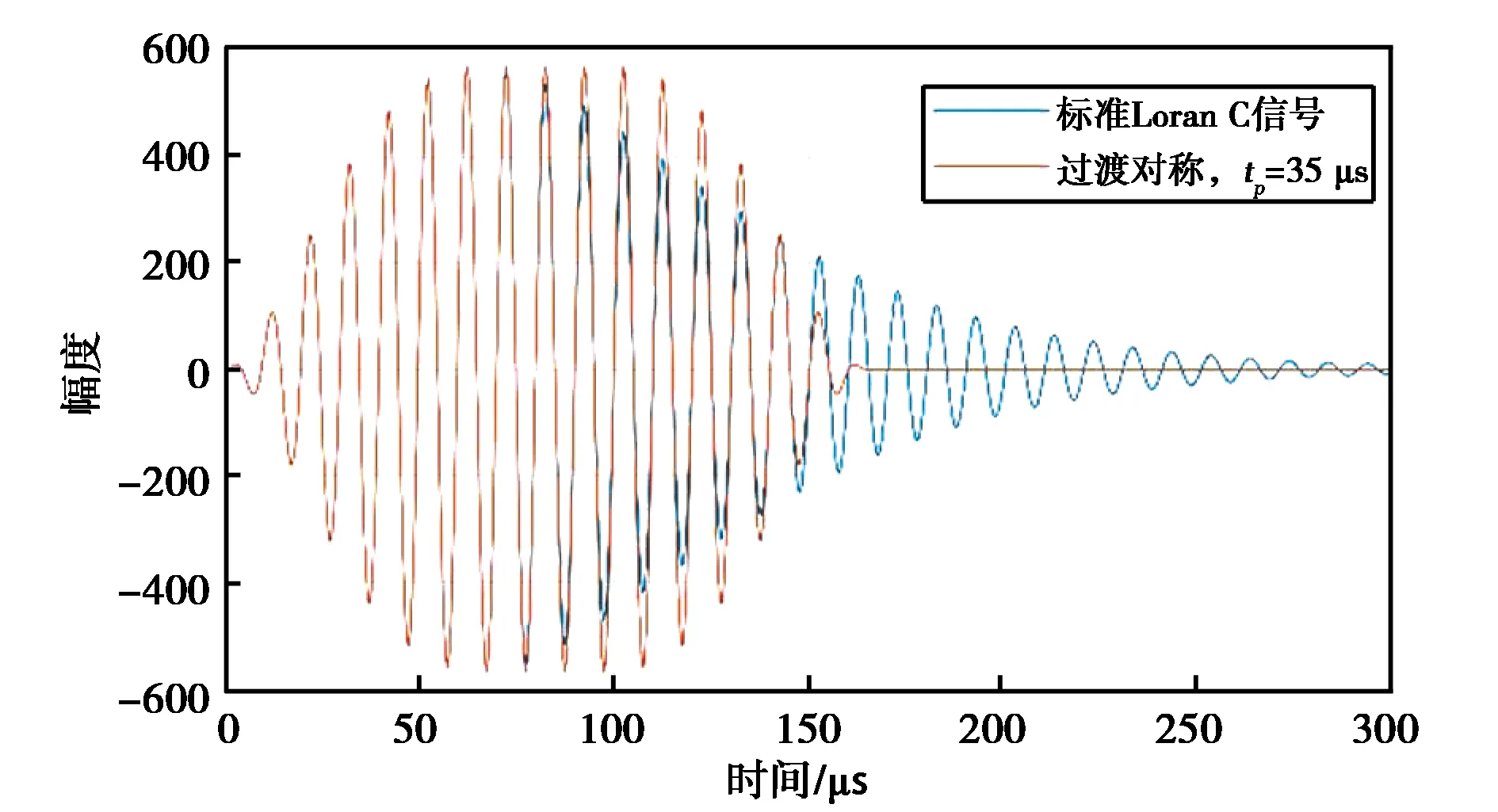
图10 过渡对称波形与标准Loran C信号波形比较示意图

中心对称的脉冲波形单个持续时间约为130 μs;对称脉冲波形单个持续时间约为(130+2tp) μs,tp取值5 μs的奇数倍;加速后沿下降脉冲波形单个持续时间约为190 μs(num-damp=80)．可知,中心对称的脉冲波形单个持续时间最短．但是为了保证信号波形的频谱特性,后沿脉冲不能下降得过快．

3 eLoran信号新型波形性能评估

3.1 信号功率谱密度性能比较

理论与实践表明时间与频率之间存在约束,缩短波形持续时间,其频谱必将产生畸变与频谱泄露．新型波形设计中参数的优化基本思路就在于在时间与频率之间找到折中．

三种衰减函数的功率谱图如图11所示．

图11 衰减函数与标准Loran C信号波形功率谱密度比较示意图

可以看到,缩短时间后新信号频谱主瓣都相应被压低．指数衰减与线性衰减方法都使得原信号频谱在约75 kHz与125 kHz处出现较宽旁瓣,影响主瓣高度．但高斯衰减函数对应的频谱泄露现象不如其他衰减方式明显,较好权衡了时间与频率两个维度之间的约束．

过渡对称波形(tp=35)频谱相比中心对称波形的频谱,如图12所示，主瓣高度并未受到较大程度的压缩,但主瓣更窄,影响信号能量集中率．下文通过该指标对以上频谱性能做进一步分析．

图12 对称波形与标准Loran C信号波形功率谱密度比较示意图

3.2 信号能量集中率

eLoran信号工作频率集中在频段90～110 kHz,超过99%信号能量集中在该工作频段[9]．本文利用帕塞瓦尔(Parseval)定理计算信号的能量,即频谱幅度的平方和(积分):

(9)

为形成对称分析(如图2中频谱所示),本文选取信号在频段0～200 kHz的频谱幅值平方和作为信号能量集中率的分母,对新型设计波形仿真信号的频谱幅值进行比较．本文为方便起见,将90～110 kHz频谱幅值的平方和与0～200 kHz频谱幅值平方和分别定义为Ew与EA,并且把两者比值作为能量集中率的参考指标,具体定义为

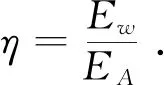
(10)

表1中详细示出新型设计波形信号功率的η,EA两个指标的计算结果．

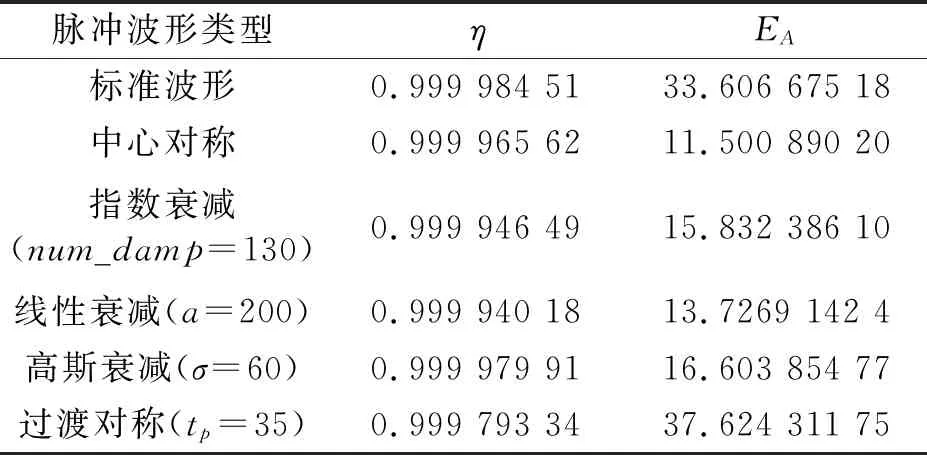
表1 新型脉冲波形信号能量指标

通过观察功率谱密度图形和计算η可知,中心对称的脉冲波形、衰减函数脉冲波形信号功率要明显小于标准Loran信号功率,4种波形(tp取值35 μs,num-damp取值130,a取值200,σ取值60)集中在90～110 kHz能量均超过99.9%．

4 eLoran信号新型波形参数优化

4.1 衰减函数波形参数优化

指数衰减函数加速后沿下降的新型脉冲波形设计方案中,减小num-damp可以加速后沿下降,缩短脉冲波形单个沿续时间,取不同的num-damp进行仿真,得到结果如表2所示.

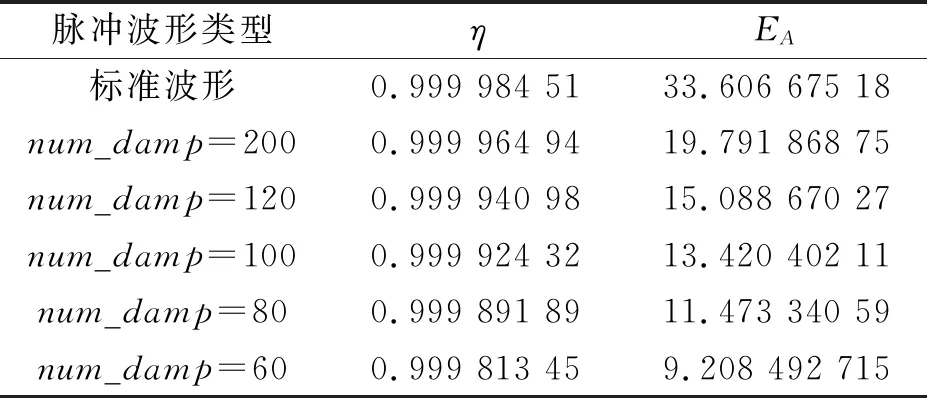
表2 指数衰减波形参数优化

脉冲波形信号辐射num-damp减小时,加速后沿下降效果增强,功率下降效果增强,但是,信号功率谱密度分散,考虑到需要降低工作频带外的信号功率,避免对其他无线电信号产生干扰,建议取值num-damp>120．

改变信号截止时间,线性衰减函数参数优化统计如表3所示.

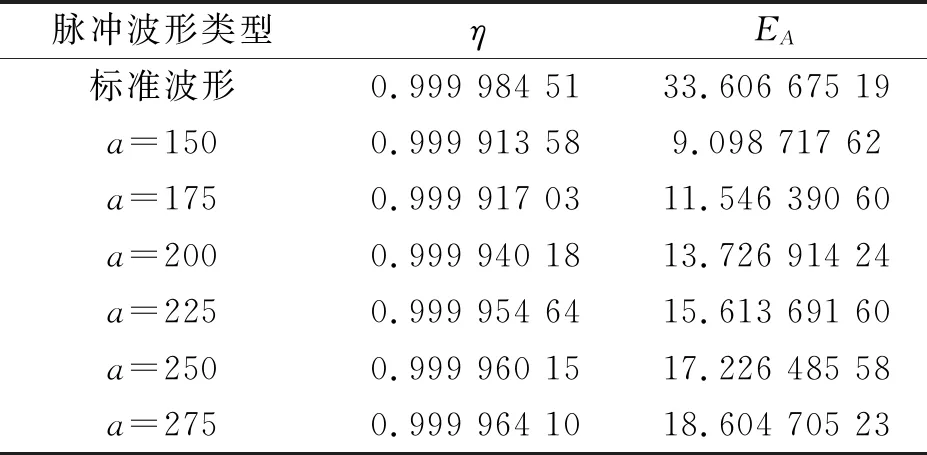
表3 线性衰减波形参数优化

以步长为25增加线性衰减函数的衰减参数发现,在a=225之后频谱约束指标优化效果并不明显,故认为线性衰减函数的优化参数可以在200～225取值,同时满足时域与频域之间的约束．

高斯衰减函数参数优化,以改变尺度参数σ为主,优化结果统计如表4所示.

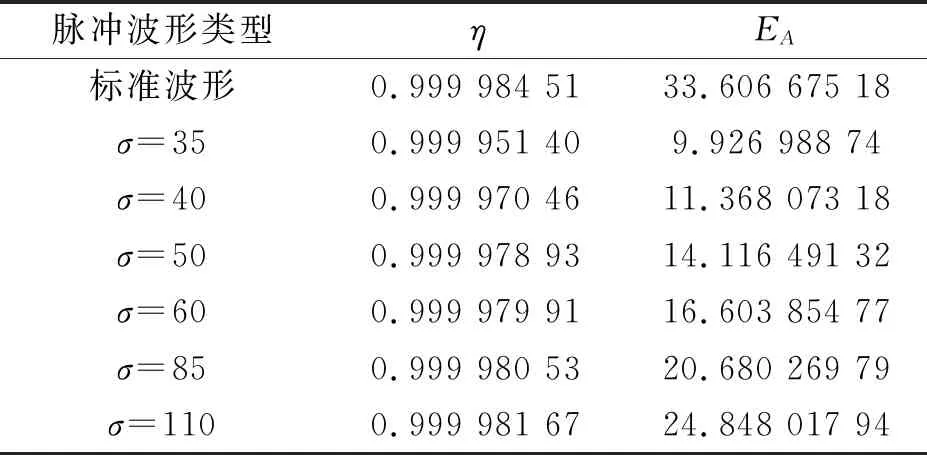
表4 高斯衰减波形参数优化

表4中高斯函数的尺度参数增加,两个频谱约束指标并不成线性关系增加,当σ=85之后,效果并不明显．可以取高斯函数的尺度参数为60左右实现后沿快速下降,同时满足减小输出功率要求．

对比三种衰减函数发现,线性衰减函数能够使得后沿波形下降最快,高斯衰减函数能够很好满足频谱指标的约束．而指数衰减函数在后半部分的后沿下降过程中变化缓慢,造成后沿波形出现较长的拖尾,但频谱约束指标方面表现得比线性衰减函数要好．在后沿波形下降与工作频段信号功率比值两个方面的共同约束下,高斯衰减函数比其他两个衰减函数的实现效果要好．而如果着重考虑波形后沿下降时间,可以牺牲较小部分工作频段信号功率选择线性衰减函数实现大幅的后沿持续时间缩短．

4.2 对称波形参数优化

对称脉冲波形设计方案中,减小tp可以缩短脉冲波形单个沿续时间,减小信号功率,取不同的参数tp进行仿真,得到结果如表5所示.

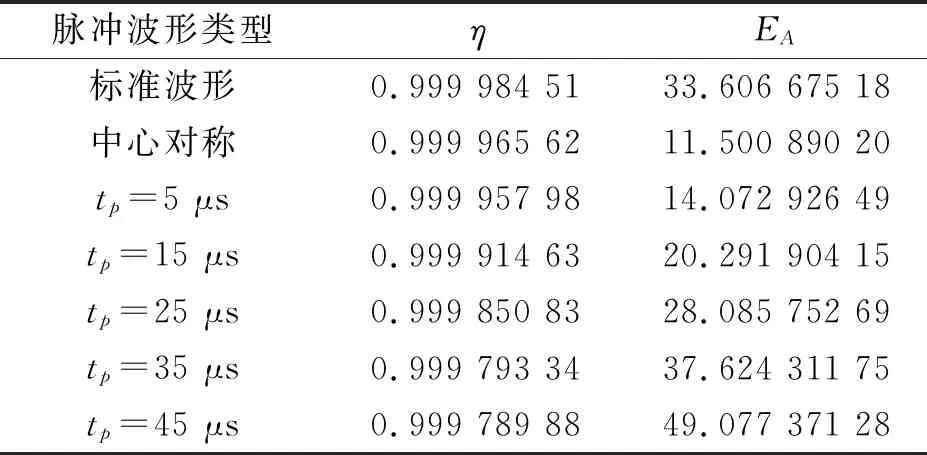
表5 对称波形参数优化

tp减小时,脉冲波形单个持续时间缩短,脉冲波形信号功率下降效果增强,信号功率谱密度集中．考虑到需要降低对系统工作频带外的干扰,建议取值tp<35 μs,并且tp越小越能保证新信号的频谱性能．

5 结 论

本文针对eLoran信号进行新型波形设计并利用频谱性能指标对波形设计参数进行优化,给出了衰减函数法、对称波形法新型信号波形的优化结果．新型信号波形大大缩短原有波形的持续时间,加速后沿脉冲波形功率下降．仿真结果证明,新型信号波形有效减小发射机功耗、提高时间域的利用率、减轻交叉干扰与天波干扰且易于实现,为新型调制方式设计提供理论基础．新型信号波形前沿与标准信号一致,且生成方式简单,不需要对定时与频率控制设备进行较大改变．但新型信号波形的可行性仍需要进一步的硬件平台实验证明．