偏置状态对组合密封性能影响的研究

赵 乐1， 索双富1， 张 琦， 张妙恬

(1.清华大学 机械工程学院， 北京 100084；2.中国矿业大学(北京) 机电与信息工程学院， 北京 100083)

引言

近年来，组合密封以其优良性能在工程技术领域得到广泛应用[1-4]。与单一密封件不同，组合密封通常由不同结构和性能的密封件组合而成，因此影响其密封性能因素较多，成为密封研究的热点[5-7]。

王成刚等[8]利用有限元分析软件建立了格莱圈有限元分析模型，并对其在不同压缩率、压力时密封面接触压力分布规律进行分析，确定格莱圈易失效位置。韩传军等[9]采用有限元方法建立齿形滑环密封模型，分析初始压缩率、介质压力和滑环齿厚对齿形滑环密封圈密封性能的影响。易攀等[10]研究了深海高压环境下不同材料硬度对组合密封结构性能的影响， 总结了O形密封圈在不同材料硬度条件下的几何变形情况以及主接触面最大接触应力与von Mises应力的分布规律。杨忠炯等[11]针对硬岩掘进机(TBM)破岩掘进作业过程中的强振动状态对格莱圈密封性能的影响进行了仿真研究，结果表明基础振动频率和幅值都会使密封间隙发生变化，从而对密封性能产生影响。

由于零件加工及装配时难以保证与设计参数完全一致，零件磨损后也导致接触状态发现变化，因此组合密封圈在使用中常常会处于偏置状态。目前关于偏置状态对组合密封性能影响的研究较少。商宏钟[12]针对红外光电探测器由高压气体旋转密封导致的泄漏问题，对组合密封结构进行改进设计，指出当转轴与回转中心不同轴时会加速密封的失效，但对偏置状态未做分析研究。

本研究利用有限元分析软件ABAQUS对于组合密封在偏置状态下的密封性能进行了仿真研究，基于仿真结果对旋转组合密封使用与维护提出建议，为密封结构改进提供一定的参考。

1 问题的提出

旋转组合密封通常由橡胶弹性体O形圈和改性聚四氟乙烯(PTFE)方圈组成，如图1所示。其密封机理是利用O形圈的预紧力使方圈贴紧密封面，当系统压力升高时，方圈将承受更大作用力从而达到高压下的密封效果[13]。

图1 旋转组合密封结构示意图

与唇形密封、O形圈等旋转密封相比，组合密封接触面大，承压能力高。但高压下运转不仅方圈易发生磨损，由于组合密封圈与回转轴接触位置固定，且方圈材料硬度相对较高，回转轴表面往往也容易出现磨损，进而影响密封面接触状态，如图2所示。

图2 回转轴表面磨损状态

仿真主要对回转轴表面与方圈的接触状态进行研究。为简化分析模型，假定密封圈及安装沟槽无偏斜，由装配误差、磨损等产生的偏斜均使回转轴接触表面处于偏置状态。

2 有限元建模与仿真

2.1 有限元建模

模型几何特征参照特瑞堡外轴用格莱圈，具体型号为TG320100，工作压力范围0～20 MPa。方圈内径100 mm，接触面宽度3.93 mm，O形圈直径3.53 mm，沟槽宽度4.2 mm，密封初始间隙0.81 mm。采用轴对称模型对组合密封圈进行几何建模，如图3所示。以回转轴参考点为中心，垂直状态时偏置角A为0，角度变化以逆时针方向为正向。按上述偏置特征进行建模，将回转轴接触面设置为不同偏置状态进行仿真。

图3 旋转组合密封轴对称几何模型

方圈弹性模量200 MPa，受压时其变形量远小于O形圈，采用线性模型进行分析。O形圈选用丁腈橡胶，建模时采用超弹性Mooney-Rivlin本构模型描述，参照文献[9]设定参数C1为1.87，C2为0.47。在单元类型选择上，方圈采用CAX4R单元，O形圈采用CAX4RH单元，以模拟橡胶材料大变形、非线性特征。回转轴与沟槽选用45号钢，材料弹性模量远大于密封圈材料，采用刚体结构建模，并将沟槽参考点固定作为初始边界条件。

旋转组合密封模型各接触面均采用罚函数法定义的面-面接触类型。根据密封结构共定义4对相互作用面，其中回转轴与方圈接触对摩擦系数设定为0.1，方圈与O形圈接触对摩擦系数设定为0.6，方圈与沟槽接触对摩擦系数设定为0.1，O形圈与沟槽的接触对摩擦系数设定为0.6。通过ABAQUS流体渗透功能自动确定密封面接触和分离的临界点，使计算结果更加客观准确。本例中对旋转组合密封圈共设置3个压力渗透面，分别为轴-方圈(压力渗透面I)，方圈-O形圈(压力渗透面II)，沟槽-O形圈(压力渗透面III)，如图4所示。

图4 流体压力渗透面

2.2 分析计算步骤

分析计算主要分为2个过程进行。首先模拟组合密封圈的初始过盈安装。按照密封手册要求，在高压下工作，密封间隙不应大于0.2 mm，设定过盈安装间隙0.17 mm。仿真中主要通过前2个载荷步实现：在第1个载荷步中，回转轴向右移动0.04 mm，使密封结构中各接触关系平稳建立起来；在第2个载荷步中，回转轴继续向右移动0.6 mm，完成组合密封圈的初始过盈装配；最后在第3个载荷步中施加流体压力载荷，完成流体加载过程。

3 仿真结果与分析

3.1 不同偏置状态下的应力分布

应力集中是导致材料疲劳失效的重要原因。通过仿真分析组合密封圈高应力区域，可预测易失效部位，为密封设计及应用提供参考。

设定流体压力为20 MPa，密封间隙为0.17 mm，分别模拟密封接触面在正向1°, 2°, 3°，以及负向-1°, -2°, -3°等不同偏置角度下进行仿真计算。组合密封圈在不同偏置状态下的von Mises应力分布如图5所示。

从仿真结果看，偏置状态下组合密封圈高应力分布区域基本一致，最大von Mises应力均出现在方圈底部近空气侧。在正向偏置状态下，随着偏置角度的增加，最大von Mises应力均有不同程度的增大，且近空气侧应力集中更加明显。同时方圈与回转轴在流体侧的接触面出现分离趋势。在负向偏置状态下，随着偏置角度的增加，最大von Mises应力也相应增大，但增大量小于正向偏置状态，且空气侧应力集中状况有所减少。

图5 不同偏置状态下组合密封圈von Mises应力云图对比

图6所示为O形圈在不同偏置状态下的von Mises应力分布。从仿真结果看，O形圈应力集中区域均出现在各接触面上。在正向偏置状态下，随着偏置角度的增加，最大von Mises应力值有所增加。在负向偏置状态下，最大von Mises应力值随偏置角度增加而有所减小。

图7所示为流体加载后，组合密封圈在不同偏置状态下的最大von Mises应力值对比图。综合上述仿真结果，在偏置状态下，密封圈最大应力值都出现一定程度的增加，容易引起密封圈的疲劳损坏。正向偏置使密封圈应力增加幅度更大，而负向偏置应力增幅相对较小。相比方圈，O形圈应力分布受偏置状态影响较小。

3.2 密封面接触压力分析

流体加载后将作用于密封接触面，密封圈接触面压力大小是实现密封的关键因素。组合密封有多对密封接触面，其中方圈与回转轴为动密封接触面，材料性能差异大，因此选择此接触面进行分析研究。

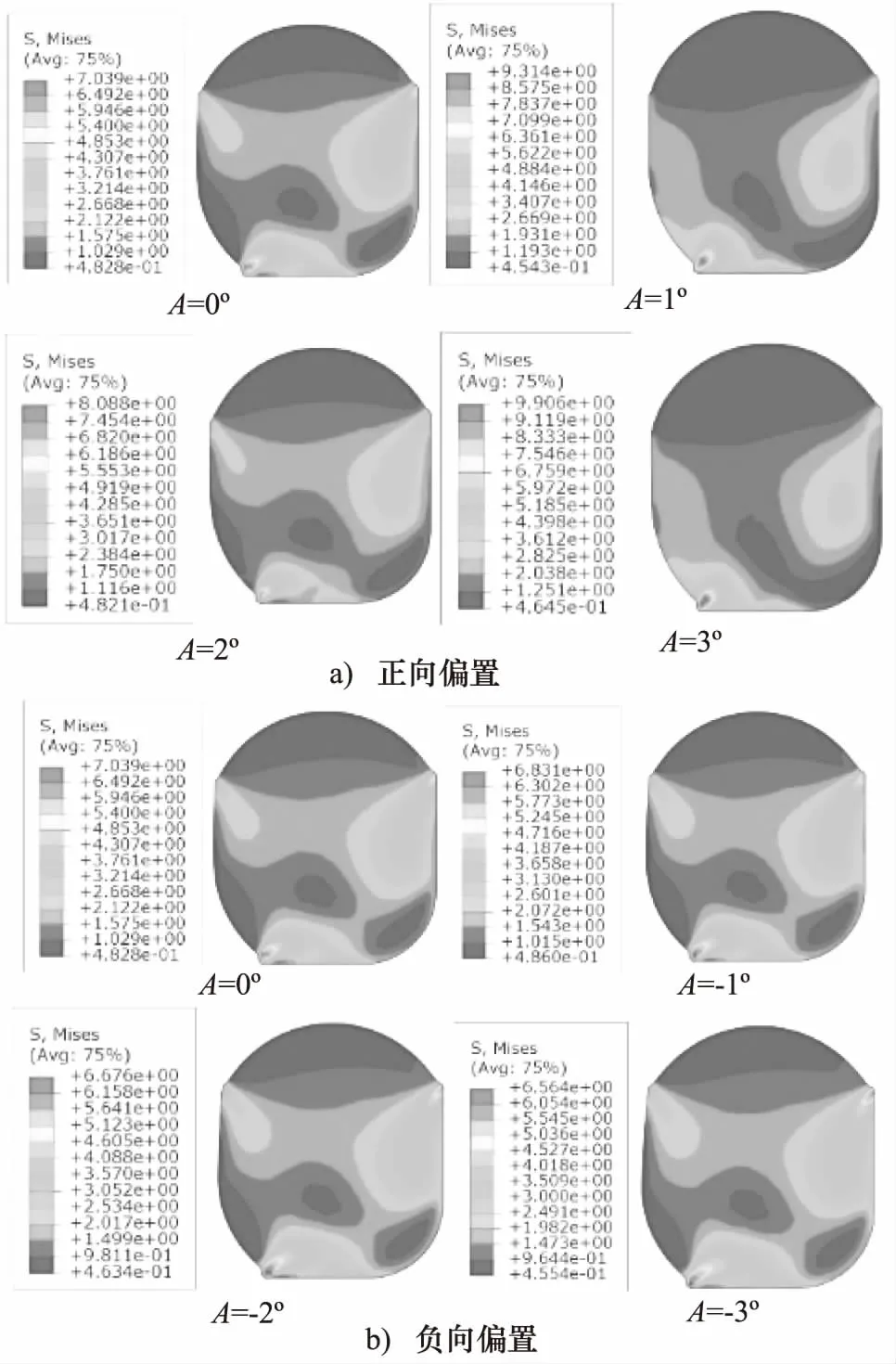
图6 不同偏置状态下O形圈von Mises应力云图对比

图7 偏置状态下组合密封圈最大von Mises应力值对比

1) 过盈安装

密封圈完成过盈安装后，通过创建路径方式，提取方圈与回转轴接触面压力值。图8为完成过盈安装后不同倾角下密封面接触压力曲线。图中横坐标为方圈与回转轴密封接触宽度l，坐标原点对应密封圈在流体侧与回转轴接触起点，纵坐标为方圈与回转轴密封接触压力p。

图8 过盈安装时方圈与回转轴接触压力曲线

由仿真结果可以看出，在过盈状态下，未偏置时，接触压力曲线沿接触宽度方向呈双峰值形态，峰值分别出现在密封面靠近流体侧和空气侧，且空气侧峰值大于流体侧峰值。峰值附近有较大的压力梯度变化，峰值间压力分布相对平缓。此压力分布可在动密封接触面上形成流体动压润滑区域，对于改善高压下密封接触面的润滑状况十分有利[14]。

在正向偏置状态下，随着偏置角度增大，两侧压力峰值呈现相反的变化趋势，流体侧峰值随偏置角度增大而减小，空气侧峰值随偏置角度增大而增大，峰值间压力也出现一定梯度变化。当正向偏置角度达到3°时，接触长度出现一定的减小，空气侧接触压力出现了大幅增长。在负向偏置状态下，方圈与回转轴密封面接触宽度基本恒定，接触压力曲线形态相似，变化趋势具有一致性。当偏置角度增大时，接触压力曲线形态基本保持不变，两侧压力峰值也呈现相反的变化趋势，但其变化趋势与正向偏置不同。流体侧峰值随偏置角度增大而增大，空气侧峰值随偏置角度增大而减小。

2) 流体加载

流体压力加载完成后，通过创建路径方式，提取方圈与回转轴接触面压力值。图9为流体压力加载后，不同倾角下密封面接触压力曲线。

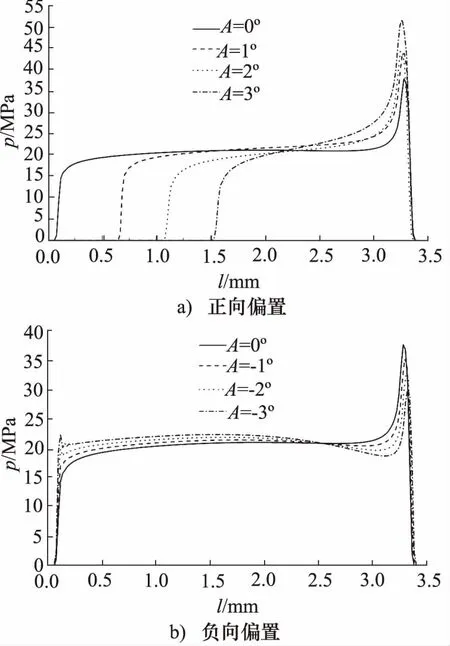
图9 流体加载后方圈与回转轴接触压力曲线

由仿真结果可以看出，在流体压力作用下，密封面各节点接触压力大幅增加，不同偏置状态下接触压力呈现较大差异。未偏置状态下，接触压力曲线沿接触宽度方向呈现单峰值形态， 峰值出现在密封面靠近空气侧，峰值附近有较大的压力梯度变化，流体侧接触面到峰值间压力相对平缓。正向偏置状态下，当偏置角度增大时，接触压力曲线形态基本不变，峰值随偏置角度增大而增大，接触长度随偏置角度增大而减小。负向偏置状态下，当偏置角度增大时，接触压力曲线形态基本保持不变，空气侧峰值随偏置角度增大而减小，流体侧接触压力出现随偏置角度增大而增大的趋势。

综合仿真结果可知，在偏置状态下，密封面接触压力都有一定的增加，从一定程度上增强了接触面上的密封能力。但由于方圈与回转轴接触面为动密封面，过高的接触压力会产生较大的摩擦损耗，特别是正向偏置状态下，容易引起密封圈过早损坏和回转轴的磨损。

4 结论

(1) 密封接触面的偏置状态对组合密封性能影响较大，特别是在高压下使用时，不同偏置状态下密封性能所受影响有较大差异;

(2) 组合密封圈应力分布受偏置状态影响较为明显。偏置状态下，方圈最大von Mises应力均出现不同程度的增大，负向偏置应力增幅相对较小。相比方圈，O形圈应力分布受偏置状态影响较小。在密封结构设计中可采用适当的负向偏置，有利于改善组合密封圈应力集中作用；

(3) 不同偏置状态对密封面接触压力有着不同影响。正向偏置状态下，接触压力峰值以及接触宽度受偏置角度影响较大，使用中应尽量避免出现正向偏置。而负向偏置状态下，接触压力曲线形态相似，变化趋势相对一致。