岩石黏性系数的超声波法测试与敏感性分析

孟世明，管华栋，王观石

(江西理工大学建筑与测绘工程学院，江西 赣州 341000)

1 岩石黏性系数测试的意义与现状

岩石的黏性系数反映了在一定载荷下，岩石变形与时间相关的特性，是表征岩石黏弹性质的重要参数之一[1-2]。进行自然界的地震分析和工程中的爆炸应力波传播规律研究时，都需要借助岩石的黏弹性本构模型，而岩石的黏性系数的取值是否合理，直接影响计算分析的正确性。因此，岩石黏性系数的准确获取和深入分析有助于岩石黏弹性模型研究，进而更好地开展岩石动力学特性研究，为地下深部岩土工程的设计和施工提供参考。

目前，岩石黏性系数测试主要有悬臂梁弯曲共振法[3-4]和动态机械分析法[5]。邓科涛等[6]基于黏弹性材料在变形过程中有能量损耗的性质，采用加载周期三角波的方法建立了室内Maxwell模型的黏性系数测试方法；李魁彬等[7]基于材料参数与梁应变响应周期及振幅衰减的关系，提出了室内Kelvin模型的黏性系数测试方法。这些室内测试方法，由于条件所限，不利于推广，更无法实现现场原位测试。岩石具有黏弹性，应力波在岩石中传播会出现振幅衰减的现象[8-9]；王观石等[10]基于应力波衰减规律，通过计算振幅的衰减系数，获得了岩体的黏性系数，实现了岩体黏性系数的应力波原位测试。但应力波测试方法无法固定应力波的频率，因而很难进行黏性系数随频率变化的研究。此外，现有研究成果中很少涉及到黏性系数对岩石密度、波速、弹性模量的相关性研究。

超声波激发的频率可控，便于重复试验，测试简单方便，既适用于室内测试，又适用于原位测试。为此，本文基于超声波在Kelvin-Voigt黏弹体的衰减规律，提出了由超声波幅值衰减规律来获取黏性系数的超声测试方法，开展了岩石黏性系数对密度、波速、弹性模量的相关性分析，并进行了岩石黏性系数随发射波频率的变化规律研究，研究成果可以为岩体力学参数测试和岩体动力学特性研究提供参考。

2 基于Kelvin-Voigt黏弹性体的岩石超声波衰减模型

岩石实际是一种黏弹性介质，通常可以用Kelvin-Voigt模型描述其本构关系。因此把岩石抽象为各向同性的Kelvin-Voigt黏弹性体，假设岩石中超声波沿X轴方向传播，其一维波动方程见式(1)。

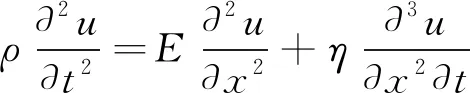
(1)

式中：u为岩石X轴方向的位移，m；t为时间，s；ρ为岩石密度，kg/m3；E为岩石弹性模量，GPa；η为岩石黏性系数，MPa·s。

若考虑超声波随空间衰减，则可假设任意t时刻的波形曲线，计算见式(2)。

u(x,t)=A0e-αxsin(ωt-kx)

(2)

式中：A0为初始振幅，m；α为衰减系数，m-1；ω为超声波发射频率，kHz；k为岩石中超声波的响应波数，m-1。

把式(2)代入式(1)可得式(3)。

(2ωηαk+Ek2-Eα2-ρω2)sin(ωt-kx)=

(ωηα2+2Eαk-ωηk2)cos(ωt-kx)

(3)

要使式(3)成立，只需满足正弦函数和余弦函数的系数为0，具体计算见式(4)。

(4)

解式(4)的二元二次方程组，并注意衰减系数α和波数k大于0，具体计算见式(5)。

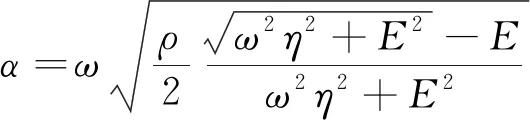
(5)

进行岩石超声波测试后，可以提取超声波发射波的最大电压辐值和接收波的最大电压幅值，不同发射波频率下的衰减系数计算见式(6)。

(6)

式中：A1为超声波在岩样发射端的最大电压幅值，V；A2为超声波在岩样透射端的最大电压幅值，V；l为岩样试件的长度，m。

联立式(5)和式(6)，可得Kelvin-Voigt黏弹性体的黏性系数，计算见式(7)。

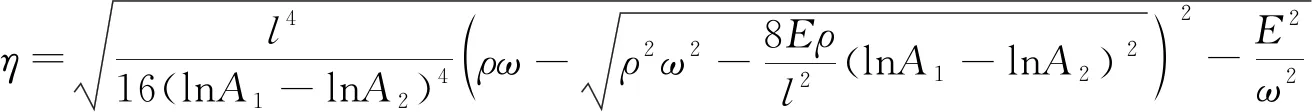
(7)

因此，通过岩石超声波试验，得到不同发射波频率下的发射波和接收波最大幅值，再把岩石的长度、密度以及弹性模量代入式(7)即可求得基于Kelvin-Voigt黏弹性体的岩石黏性系数。

3 岩石超声波试验

岩石超声波测试采用的测试系统包括：固纬AFG-3000任意波形信号发生器、固纬GDS-2000A数字存储示波器、HA-405高压放大器、汕头超声生产的50K-P40F声波换能器，以及高灵敏度声波信号接收器和稳压电源。通过波形信号发生器改变超声波发射频率，分别进行20 kHz、25 kHz、30 kHz、35 kHz、40 kHz、45 kHz、50 kHz的岩样超声波波形测试，保存并导出波形数据。

试验选用的3个岩样均取自福建省某矿山，岩样物理力学参数见表1，其中岩样的弹性模量是在超声波测试完成后由单轴压缩试验测得。3个岩样的密度、横波波速和弹性模量都是递增的，纵横波波速比是递减的，而纵波波速的变化没有规律。

4 岩石黏性系数测试结果及敏感性分析

3个岩样在20 kHz和50 kHz频率下的超声波发射波和接收波波形如图1所示。3个岩样的发射波波形几乎相同，接收波受岩样密度、弹性模量和黏性系数等参数影响，波形差异明显。发射波频率为20 kHz时，3个岩样接收波的最大幅值分别为0.43 V、0.38 V和0.35 V；发射波频率为50 kHz时，3个岩样接收波的最大幅值分别为0.24 V、0.16 V和0.2 V。同一个岩样的接收波随发射波频率增加而大幅度衰减，符合应力波在岩石中频率越高衰减越快的传播规律。

表1 岩样参数

图1 3个岩样在不同频率下的超声波波形

Fig.1 Ultrasound waveform of three rock specimens at different frequencies

根据超声波测试记录的波形数据，提取发射波的最大电压辐值和透射波的最大电压幅值，再利用式(7)计算不同发射波频率下的黏性系数，计算结果见表2。

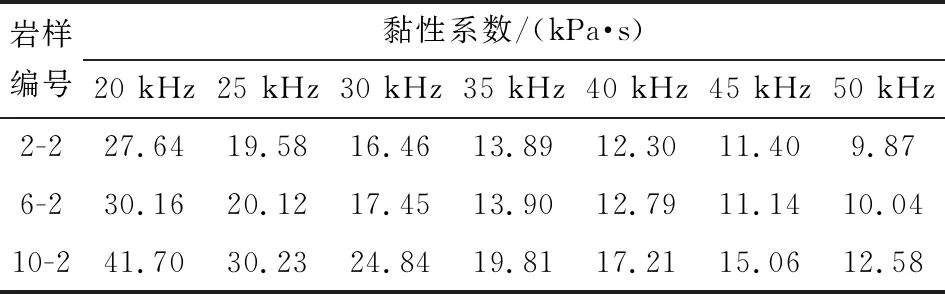
表2 不同发射波频率下的黏性系数

1) 岩样黏性系数与密度、波速及弹性模量的相关性分析。表2中，同一个发射波频率下(除45 kHz外)，岩样2-2的黏性系数最小，岩样6-2次之，岩样10-2最大，这与岩样密度、横波波速、弹性模量的大小排序相同，而与岩样纵横波波速比的大小排序相反；3个岩样的纵波波速变化没有规律，因此不进行黏性系数与纵波波速之间的变化分析。分别计算3个岩样从发射波频率为20 kHz到50 kHz的黏性系数减小率，岩样2-2为64.2%，岩样6-2为66.7%，岩样10-2为69.8%，岩样黏性系数的减小率与岩样密度、横波波速、弹性模量的大小排序相同，与岩样纵横波波速比的大小排序相反，即呈现与黏性系数相似的规律。

为了更好地分析岩样黏性系数与密度、波速及弹性模量的相关性，引入相关系数，计算见式(8)。相关系数为正，表示两个参数为正相关，反之则为负相关；相关系数的绝对值越大，说明两个参数相关性越强，对其变化也越敏感。

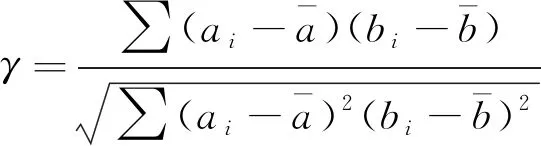
(8)

利用式(8)分别计算不同发射波频率下岩样的黏性系数与其密度、波速、弹性模量的相关系数，结果见表3。

由表3可知，不同发射波频率下岩样的黏性系数与弹性模量的相关系数最大，为0.985～1，属于正相关；不同发射波频率下岩样的黏性系数与纵横波速比的相关系数次之，为-0.818～-0.927，属于负相关；不同发射波频率下岩样的黏性系数与密度和横波波速的相关系数较为接近，都为正相关；不同发射波频率下岩样的黏性系数与纵波波速的相关系数最小，为-0.215～0.012，除发射波频率20 kHz外都表现为负相关；因此，综合分析表明：同一发射波频率下，岩样的黏性系数对弹性模量的变化最为敏感，而对纵波波速的变化最不敏感，可以用弹性模量的变化来估算黏性系数的变化。

此外，分别计算岩样从发射波频率为20 kHz到50 kHz的黏性系数减小率与各参数的相关性系数，发现：黏性系数随频率的减小率与纵横波速比的相关系数最大， 相关系数为-0.996，属于负相关；其次是弹性模量， 其相关系数为0.940， 属于正相关； 最小为纵波波速， 其相关系数为0.300，也属于正相关。

表3 不同发射波频率下岩样的黏性系数与各参数的相关性分析

2) 岩样黏性系数拟合参数与密度、波速及弹性模量的相关性分析。不同发射波频率之间相互比较，发射波频率为20 kHz时岩样的黏性系数最大，发射波频率为50 kHz时岩样黏性系数最小，即岩样的黏性系数与发射波频率呈负相关。分别绘制不同岩样黏性系数随超声波发射频率变化的散点图，并用负指数拟合，如图2～4所示。

由图2～4可知，可以把3个岩样的拟合公式可以统一为式(9)。

η=C1e-C2ω

(9)

式中：C1为拟合参数，kPa·s；C2为拟合参数，μs。

利用式(8)分别计算3个岩样的拟合参数与其密度、纵横波波速、弹性模量的相关系数，结果见表4。

由表4可知，岩样黏性系数的拟合参数C1与弹性模量相关系数最大，为0.995，属于正相关；C1与纵横波速比的相关系数次之，为-0.942，属于负相关；C1与纵波波速的相关系数最小，为0.053；拟合参数C1对弹性模量的变化最为敏感，而对纵波波速的变化最不敏感，可以用弹性模量的变化来估算C1。岩样黏性系数的拟合参数C2与纵横波波速比的相关系数最大，为-0.996，属于负相关；C2与横波波速和密度的相关系数较为接近， 都大于C2与弹性模量的相关系数， 都属于正相关；C2与纵波波速的相关性最小，为0.463；拟合参数C2对纵横波波速比的变化最为敏感，而对纵波波速的变化最不敏感，可以用纵横波波速比的变化来估算C2。

图2 岩样2-2不同发射波频率下的黏性系数

Fig.2 Viscous coefficient of rock specimen 2-2 at different incident wave frequencies

图3 岩样6-2不同发射波频率下的黏性系数

Fig.3 Viscous coefficient of rock specimen 6-2 at different incident wave frequencies

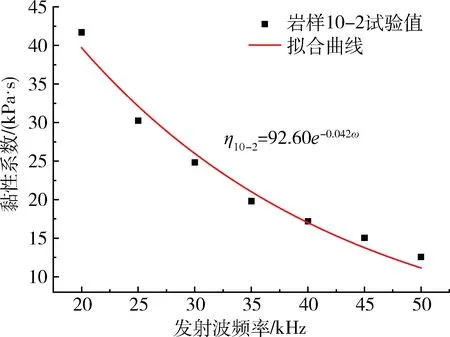
图4 岩样10-2不同发射波频率下的黏性系数

Fig.4 Viscous coefficient of rock specimen 10-2 at different incident wave frequencies

表4 岩样黏性系数的拟合参数的相关性分析

5 结 论

1) 本文推导了Kelvin-Voigt黏弹性体的黏性系数计算公式见，从而可通过密度、弹性模量、频率以及超声波发射波、接收波幅值确定岩石的黏性系数。

2) 通过岩石超声波试验，获得了7种发射波频率下的岩石黏性系数，岩石黏性系数是非定常的，会随发射波频率的变化而变化。

3) 岩石黏性系数与其密度、纵横波波速、弹性模量呈正相关，与其波速比呈负相关，岩石黏性系数对弹性模量的变化最为敏感，而对纵波波速的变化最不敏感，可以用弹性模量的变化来估算黏性系数。

4) 岩石黏性系数与发射波频率近似呈负指数函数关系，拟合关系式可以统一用式(9)表示，拟合参数C1对弹性模量的变化最为敏感，而对纵波波速的变化最不敏感，拟合参数C2对纵横波波速比的变化最为敏感，而对纵波波速的变化最不敏感。

致谢衷心感谢国家自然科学基金项目(编号：41462009)和江西理工大学人才培养项目(编号：3401223395)对本文试验的资助，特别感谢同行专家孙利辉副教授对本文公式的运算过程和运算结果所做的审查纠正工作。