负荷对载重子午线轮胎生热影响的仿真分析

2020-05-22 00:56王安迎

弹性体 2020年2期

王安迎，王伟

(青岛科技大学橡塑材料与工程教育部重点实验室，山东青岛 266042)

据统计，在载重货车道路交通事故中，有80%以上是由于超限超载运输引起[1]，汽车超载会对轮胎的使用安全造成很大影响。轮胎是车辆重要的组成部分之一，对车辆的行驶安全有着直接影响。车辆行驶过程中轮胎受到交变载荷作用，由于橡胶材料的滞后性，引起轮胎温度升高[2]，进而导致其物理机械性能下降，如果长时间处于高温状态下还会加速轮胎老化，影响到车辆行驶的安全性[3]。因此，研究轮胎在稳态滚动过程中的温度场分布，不仅对轮胎设计[4]和生产具有非常重要的意义，而且对轮胎安全使用具有重要的指导意义。

目前，研究轮胎生热温度场的方法主要有实验实测法和数值模拟法[5]。实验实测法只能局限于测量轮胎的表面温度或者轮胎内部某测温点的温度[6-7]，实验周期长、费用高，实验结果易受实验条件和环境的影响。数值模拟法可根据轮胎的工作状态、材料特性来对轮胎进行热力学模拟，从而预测轮胎内部温度场的分布状况。

轮胎温度场的热力耦合过程非常复杂，本文主要运用单向解耦[8][9]276思想进行分析研究，运用ABAQUS软件，对12R22.5载重子午线轮胎稳态滚动温度场进行有限元分析，并将实验结果与模拟结果进行对比验证。

1 轮胎稳态滚动仿真模型的建立

在ABAQUS软件中要实现轮胎的稳态滚动，首先要建立几何模型，然后分别为不同橡胶部件选择合适的本构模型，最后对轮胎模型进行静态载荷和稳态滚动分析。

1.1 材料模型的选取

轮胎是由橡胶、帘线和钢丝圈等材料复合而成，因此用ABAQUS软件对轮胎进行建模时，不同材料需要选取不同的材料模型。

橡胶属于超弹性材料，考虑到计算精度、计算效率和模型收敛性。本文采用Yeoh模型[10]108，选用12R22.5载重子午线轮胎，但是不同的帘线层功能不一样，因此不同的帘线层有不同的帘线角、间距、截面面积、单根帘线匝数。本文选用加强筋(Rebar)单元，将其定义在单元面上，再将单元面嵌入到橡胶单元上。

1.2 三维模型的建立

首先建立轴对称模型，赋予其材料属性、接触属性。为了提高计算效率，在轴对称模型中实现轮辋装配和对轮胎施加充气压力的过程，然后将其应力、应变结果传递到三维模型。图1中轮胎三维模型的建立是通过修改INP文件实现的。

图1 轮胎三维有限元模型生成过程

在INP文件中通过*SYMMETRIC MODEL GENERATION指令将轮胎轴对称模型旋转成四沟槽轮胎三维模型。

1.3 有限元模型及验证

三维几何模型建立以后，对轮胎施加33.5 kN的标准载荷和830 kPa的标准充气压力，将模拟结果与实验结果[10]108进行对比，结果如表1所示。

表1 轮胎静载荷下模拟值与测试值比较1)

1) 实测接地面积中实测值为41 156 mm2、模拟值为41 698.5 mm2、相对误差为1.196%。

从表1可以看出，在标准工况下，12R22.5轮胎的充气外直径、充气断面宽、标准载荷断面宽和接地面积模拟值与实验值吻合很好。

在施加标准载荷过程中，轮胎受到的垂直负荷与轮胎下沉量的关系见图2。

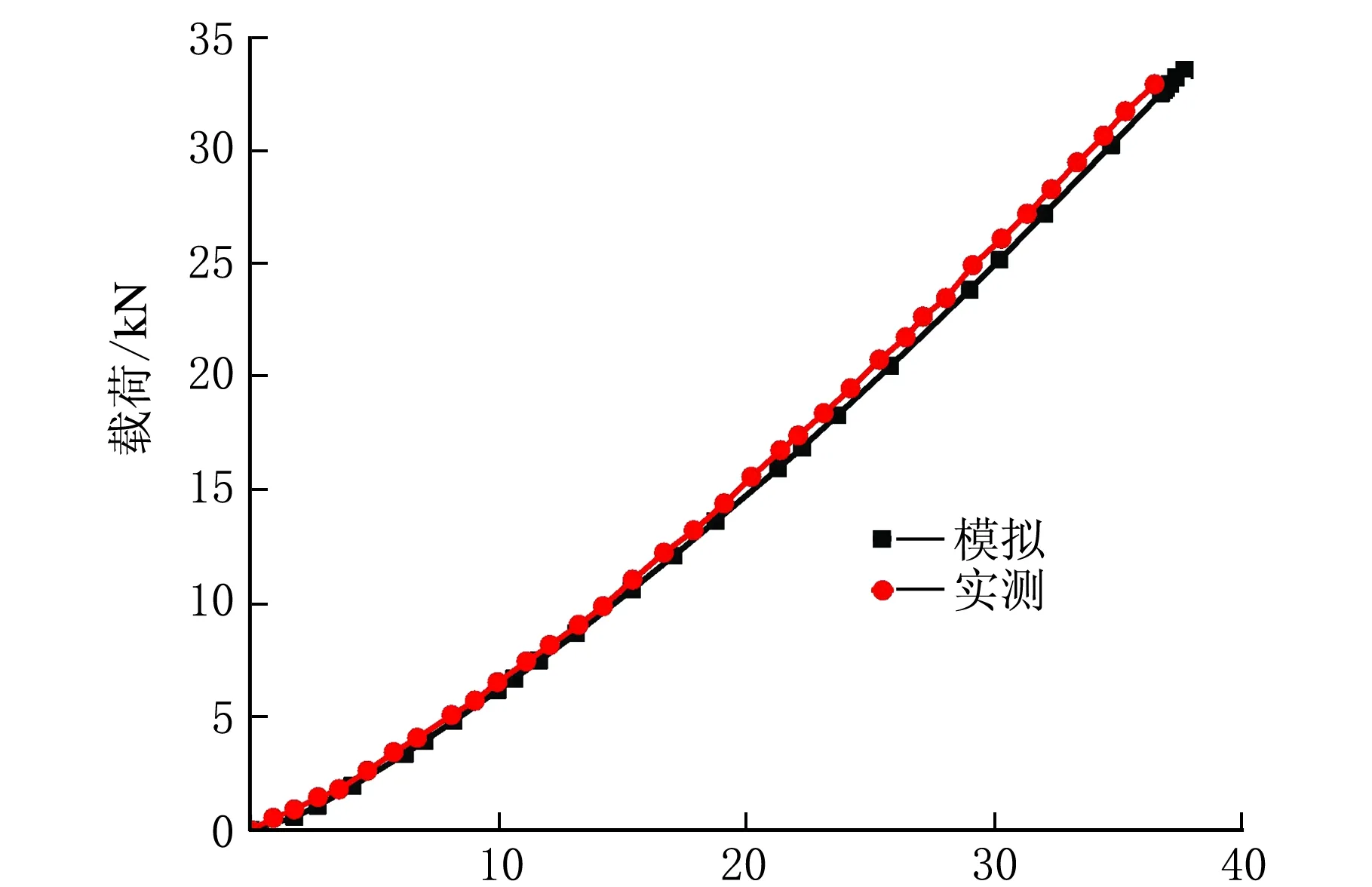
下沉量/mm图2 轮胎模拟与实测静刚度曲线比较

从图2可以看出，轮胎静刚度曲线和实测值吻合较好，刚度接近，结果与相关文献一致[9]277[11-12]，验证了有限元模型的准确性。

2 橡胶材料机械能损耗的计算

2.1 动态力学损耗模型的建立

当轮胎滚动时，受到交变外场的作用，产生周期性的应力、应变。橡胶属于黏弹性材料，在交变外场的作用下，应变响应滞后于应力，产生相位角(δ)，其应力-应变响应的相位关系如图3所示，φ为橡胶周期运动过程的相位。

φ图3 橡胶应力-应变响应的相位关系

假设交变的应力、应变符合正弦变化规律，则可以表示为式(1)和式(2)。

σ=σ0sin(ωt)

(1)

ε=ε0sin(ωt+δ)

(2)

式中：t为时间，s；δ为相位角，rad；ε为应变；ε0为应变幅值；σ为应力，MPa；σ0为应力幅值；ω为交变频率，Hz。

当轮胎滚动时，在交变载荷作用下橡胶材料受到压缩和回弹作用，应变响应滞后于应力，因此在一个周期内形成滞后圈，其面积等于材料在一个周期内单位体积所损耗的能量，见图4。

图4 一个周期内应力-应变曲线

根据图3、图4和式(1)、式(2)的关系可知，一个周期内单位体积的黏弹性损耗W可以表示为式(3)和式(4)。

(3)

对其积分得到：

W=πσ0ε0sinδ

(4)

式中：sinδ在δ取值较小时与损耗正切tanδ近似相等，因此可用tanδ来表示。

2.2 机械能损耗计算

橡胶材料滞后损失是由材料的应力应变引起的，对于不可压缩黏弹性材料，根据变形理论，可以用等效应力和等效应变来表示材料的形变。等效应力和等效应变分别用式(5)和式(6)表示。

(5)

(6)

式中：σx、σy、σz分别为x、y、z三个方向的应力分量；σxy、σyz、σxz分别为xy、yz、xz三个平面的剪切应力分量；εx、εy、εz分别为x、y、z三个方向的应变分量；εxy、εyz、εxz分别为xy、yz、xz三个平面的剪切应变分量。

由于轮胎稳态滚动时周期内轮胎产生的应力和应变属于非简谐波，因此需要经过傅立叶转变将周期内应力、应变产生的机械波分解为数个不同简谐波的叠加，然后可得到应力和应变的幅值，傅立叶展开公式如式(7)和式(8)所示。

(7)

(8)

根据式(4)～式(6)得到单位体积上的黏弹性损耗，如式(9)所示。

(9)

式中：N为傅立叶级数。

从ABAQUS软件分析结果中提取轮胎模型节点上的应力、应变数据，然后根据上述分析过程编写能量损耗程序，在MATLAB软件中进行傅立叶展开，通过式(9)计算得到橡胶材料单位体积上的能量损耗。

2.3 热源和边界条件的确立

在轮胎三维建模时，周向分为180份，当轮胎达到稳态滚动时，每个截面在周期内有着相同的应力、应变状态，因此可以认为：(1)轮胎周向上相同部位的生热量相同；(2)轮胎周向上的热边界条件相同；(3)轮胎上橡胶材料为各向同性。

2.3.1 热传导机理和内热源计算

通过以上假设，可以将三维热传导模型转化为轴对称模型的稳态温度场问题。根据傅立叶定律和热力学第一定律，轮胎轴对称模型的热平衡方程如式(10)所示。

(10)

式中：kx、ky为胶料沿x和y方向的导热系数，W/(m·K)；Q为热生成率，W/m2。经网格离散后节点上的热生成率如式(11)所示。

Q=W/T

(11)

式中：T为周期，s；W为黏弹性损耗，J/m3；Q为热生成率，W/m3。

节点上的热生成率由MATLAB程序计算得到，然后通过*CFLUX关键词定义节点上的热源。

2.3.2 热边界条件的确定

在传热学[13]中有边界温度函数、边界热流密度、固体与流体接触三类边界条件，对流换热是主要影响因素。

Clark J D等[14]运用试错法研究了轮胎各部位的对流换热系数，并得出了式(12)～式(14)关系式，即胎侧对流换热系数hS为hB到hT的线性变化。

hT=2.2v0.84

(12)

hB=0.4hT

(13)

hc=hB

(14)

式中：hT、hB和hc分别为胎面、内表面和轮辋的对流换热系数；v为行驶速度，km/h。

3 结果与讨论

3.1 标准工况下轮胎温度场

利用原轴对称力学模型建立轴对称热分析模型，然后增加轮胎内外侧的对流换热系数和环境温度。标准工况条件下，通过计算得到车速为100 km/h时的温度场分布，如图5所示。

图5 标准工况下轮胎温度场分布

图5中的轮胎高温区主要位于胎肩、胎面和三角胶部位，其中胎肩的生热最高，为124.0 ℃，胎侧的温度较低。由于实验条件的限制，本研究没有对此规格的轮胎进行稳态滚动生热实验，本文与相关文献[15]进行对比，文献中对11R22.5载重子午线轮胎稳态滚动温度场进行了系统研究，与本研究轮胎规格相近。文献中在标准工况下，速度为100 km/h时，轮胎生热的高温区域位于胎肩、胎面和三角胶，最高温度为126 ℃，与本研究的生热部位相同，最高温度也基本相近。胎肩部位温度高，主要是因为胎肩部位受到的应力应变较大，生热高；同时由于胎肩部位的材料厚度大、散热困难，使得胎肩温度高。三角胶部位温度高，主要是因为轮胎周期滚动时，该部位的曲挠变形较大，导致能量损失较大，生热高，同时三角胶部位的材料较厚、散热困难。

3.2 负荷对轮胎温度场的影响

现实生活中，汽车超载是诸多交通事故发生的主要原因。为了探究负荷对轮胎生热温度场的影响，考察了不同负荷下轮胎稳态滚动生热温度场的分布规律。在行驶速度为100 km/h 时，分别模拟了负荷为60%、80%、100%、120%、140%、160%、180%和200%标准载荷状态下轮胎生热温度分布，如图6所示。

(a) 60%标准载荷

(d) 120%标准载荷

(e) 140%标准载荷

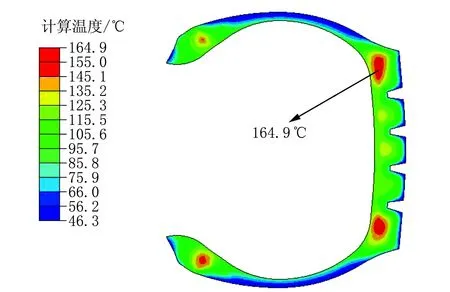
(f) 160%标准载荷

(g) 180%标准载荷

(h) 200%标准载荷图6 不同负荷下轮胎的温度场分布

从图6可以看出，随着负荷的不断升高，轮胎生热不断增加，轮胎的整体温度逐渐上升。在60%和80%标准载荷时，轮胎高温区域出现在胎面、胎肩和三角胶区域，温度最高点位于胎面花纹块位置；从图6(e)～(h)可以看出，当达到标准载荷时，轮胎高温区域仍然出现在胎面、胎肩和三角胶，但是温度最高点已经从胎面部位向胎肩部位转移，随着负荷不断增大，胎肩部位的温度越来越高，且温度最高点位置不断向外部胎侧转移。

图7和图8是60%和120%标准载荷下的接地中心断面形变与接地印痕压力分布。

通过图6～图8对比可知，当负荷较小时，胎面花纹块是主要形变部位和受力部位，所以花纹块部位温度高。当负荷超过标准载荷时，接地面积增大，轮胎断面加宽，主要受力部位和变形部位从胎面转移到胎肩部位，加之该部位橡胶很厚，不易散热，所以温度最高点开始转移到胎肩部位，且随着负荷的不断增大，超载现象加剧了轮胎出现肩空、肩裂和爆胎的可能性，极易造成重大交通安全事故。