淬硬钢模具铣削动力学和稳定性研究综述

姜彦翠 崔健 刘献礼 仇焱

摘 要：淬硬钢模具由于硬度高、型面复杂多变，铣削加工过程易产生颤振，颤振会影响工件表面质量制约铣削效率，因此对淬硬钢模具铣削加工过程进行动力学分析和稳定性预测已经变得越来越重要了。淬硬钢模具铣削稳定性主要和加工系统动态特性与动态铣削过程两方面有关，因此，对淬硬钢模具加工系统动力学特性、动态铣削过程动力学建模和铣削稳定性分析3个方面的研究进行归纳和总结。在淬硬钢模具加工系统动力学特性研究方面，主要对锤击模态试验、导纳耦合子结构分析法以及解析法的基本原理、实际应用和局限性进行阐述;在动态铣削过程动力学建模方面，主要对淬硬钢模具复杂曲面动态切削厚度建模和刀具-工件表面接触区域提取方法进行综述;在铣削稳定性分析方面，主要对几种典型颤振稳定域预测方法的实际应用进行了总结。同时指出淬硬钢模具复杂曲面铣削动力学建模与稳定性研究方面存在的不足。

关键词：淬硬钢模具、铣削动力学、铣削稳定性、复杂曲面

DOI：10.15938/j.jhust.2020.01.005

中图分类号： TG506;TH113

文献标志码： A

文章编号： 1007-2683（2020）01-0029-07

Abstract：Because of the characteristics of hardened steel mold with high hardness and surface characteristics of the complex， the hardened steel mold in the milling process is easy to produce flutter. The flutter will affect the workpiece surface quality and restrict milling efficiency， therefore， the dynamic analysis and stability prediction of hardened steel mould in the milling process have become more and more important.The hardened steel mould milling stability is mainly related to dynamic characteristics of the processing system and dynamic milling process， therefore， the article summarized the research on three aspects of hardened steel mold ，the dynamic characteristics of the machining system， the dynamic milling process dynamics modeling and the milling stability analysis. In the aspect of dynamic characteristics of hardened steel mold machining system， hammer mode test， admittance coupling substructure analysis method and the basic principles， practical applications and limitations of analytical method are mainly described. In the aspect of the dynamic milling process dynamics modeling， the dynamic cutting thickness modeling of complex surface of hardened steel mold and the extraction method of tool-workpiece surface contact area are mainly reviewed. In the aspect of milling stability analysis， the practical application of several typical chatter stable domain prediction methods is summarized. At the same time， the article points out the existing problems of milling dynamics modeling and stability study of the complex surface of hardened steel mold.

Keywords：hardened steel mold; milling dynamics; milling stability; sculptured surface

0 引 言

淬硬鋼模具在汽车、家电、轻工等产品的生产过程中都有广泛的应用。淬硬钢模具具有工件材料硬度高、型面复杂多变，且表面加工质量和加工精度要求高等特点。目前主要采用铣削的加工方式，相对于其它切削加工形式，铣削加工具有切削力小、切削温度低、加工变形小、加工能力强、材料去除率高等诸多优点，适用于平面、斜面、型腔及曲面的加工，因而被广泛应用于金属材料零件的制造中。但淬硬钢模具铣削加工过程中存在明显的问题，即铣削颤振，颤振如果不加以控制，会在所加工的表面产生振纹，使表面粗糙度增加，影响加工零件的精度，严重时甚至可能会损坏刀具和机床，因此对淬硬钢模具铣削加工过程中颤振的抑制，保证铣削过程的稳定性是十分必要的[1-2]。

淬硬钢模具铣削稳定性主要和加工系统动态特性与动态铣削过程两方面有关，如式1所示，式中的加工系统的模态质量、模态阻尼和模态刚度反映的是加工系统的动力学特性，而动态铣削力反映的是动态铣削过程。

本文主要针对淬硬钢模具铣削动力学和稳定性研究进行综述，主要对淬硬钢模具加工系统的动态特性、淬硬钢模具复杂曲面动态加工过程建模以及铣削稳定性分析三方面的国内外研究现状和各自应用范围进行归纳和总结。

1 加工系统动态特性研究现状

淬硬钢模具铣削加工系统动态特性是影响铣削稳定性的主要因素之一，在研究铣削稳定性之前首先要获得加工系统动力学特性。

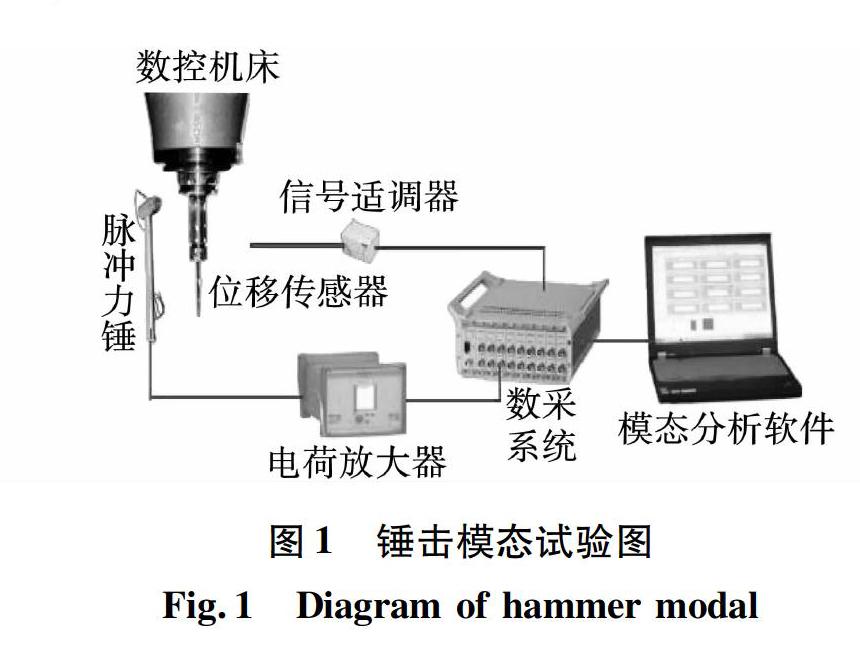
如图1所示，锤击模态试验是目前为止获得加工系统动力学特性最直接的方法。该方法利用力锤敲击进行激励，然后利用电荷放大器转换成电信号，发送到数据采集系统;利用传感器收集刀具振动响应信号，再经过模态分析软件进行模态分析，获取加工系统模态参数。该方法可以真实反映加工系统的动态特性，但是由于该方法费时费力，重复性差等缺点，所以该方法一般作为理论分析方法的参照和验证。

由于锤击模态试验法有以上的缺点，针对这些缺点也出现了一些其他研究方法，例如导纳耦合子结构分析法，该方法是由Schimitz等[3]提出，将理论分析和模态试验相结合，属于半理论方法，主要是将加工系统拆分成几个部分，结合面部分用弹簧阻尼单元模拟，然后通过模态试验进行结合面的参数辨识，进而进行加工系统动力学特性的预测。在此之后，又有Filiz等[4]改进了子结构划分和结合面模拟单元，建立了考虑结合面接触特性的加工系统动力学模型。Albertelli等[5]将刀具-刀柄-主轴系统分为两个子结构，考虑弯曲振动中的转动响应的影响，利用有限差分方法确定了主轴-刀柄子结构的平动和转动频响函数。Mancisidor等[6]将刀具-刀柄-主轴系统分为两个子结构，考虑刀具和刀柄的剪切变形效应，利用固定边界的Timoshenko梁预测了刀具刀尖导纳，并指出在导纳耦合过程中，可以通过这种方法减小模态截断导致误差。Ozsahin和Altintas[7]将刀具-刀柄-主轴系统分为三个子结构，考虑了刀具刀刃部分的截面惯性矩，研究了刀具的不对称性对刀具刀尖导纳的影响。以上研究虽然保证了在换刀情况下不需要重复试验，但是一旦改变结合面接触特性参数就需要重新进行辨识。针对这个通用性差的问题，赵万华[8]等提出一种理论分析法，該方法主要是针对主轴系统，考虑了刀具-夹套、夹套-刀柄以及刀柄-主轴结合部接触特性，建立结合面接触特性的通用理论模型，并且引入到主轴系统动力学模型中。在此基础上，文[9]考虑主轴系统铣削状态下产生的轴向铣削力和离心力对主轴结合面接触特性的影响，建立主轴系统动力学模型。

针对主轴静止状态和加工状态的差异，还有一些学者进行研究，主要是通过理论分析法对主轴加工状态进行建模，主要考虑铣削加工过程中主轴旋转情况下的轴承刚度软化效应、结合面刚度软化效应、离心力及陀螺效应对加工系统的影响。如Rantatalo等[10]采用有限元法建立主轴模型，考虑了陀螺力矩和主轴转速对主轴系统动力学的影响;曹宏瑞等[11-12]考虑了离心力和陀螺效应的对主轴系统动力学的影响，采用Timoshenko梁单元和转盘单元建立主轴转子、转盘、主轴箱等部件有限元模型，并对Jones轴承模型进行扩展建立高速滚动轴承非线性模型。Cao 等[13]研究了主轴与机床之间的耦合建模问题，利用试验法建立了机床的等效模型并确定出主轴与机床之间的连接刚度，建立了一个包括刀柄与刀具、主轴以及机床等结构在内的动力学集成模型，并以此为基础对高速主轴的加工性能进行预测仿真。之后，文[14]在Cao所建立模型的基础上进行了修正，考虑了结合面之间的动态特性，提出一种基于频率响应函数的有限元模型修正技术。

可以看出学者们越来越重视铣削加工状态下的加工系统动态特性的研究，目前这方面研究主要集中在考虑主轴系统在高速旋转加工状态下的轴承刚度软化、结合面刚度软化、离心力和陀螺效应等因素对加工系统动态特性的影响。而对于淬硬钢模具铣削加工很大程度上应用了高速铣削加工技术，因此上述的各项影响因素在研究时均应考虑。同时由于淬硬钢模具工件材料硬度高、型面复杂多变等特点，铣削过程中产生很大的铣削载荷和振动，因此在研究淬硬钢模具铣削加工系统动力学特性时还应考虑铣削加工过程中的物理因素对铣削加工系统动力学特性的影响，而这方面的研究还不是很多，有待于进一步探索研究。

2 动态铣削过程研究现状

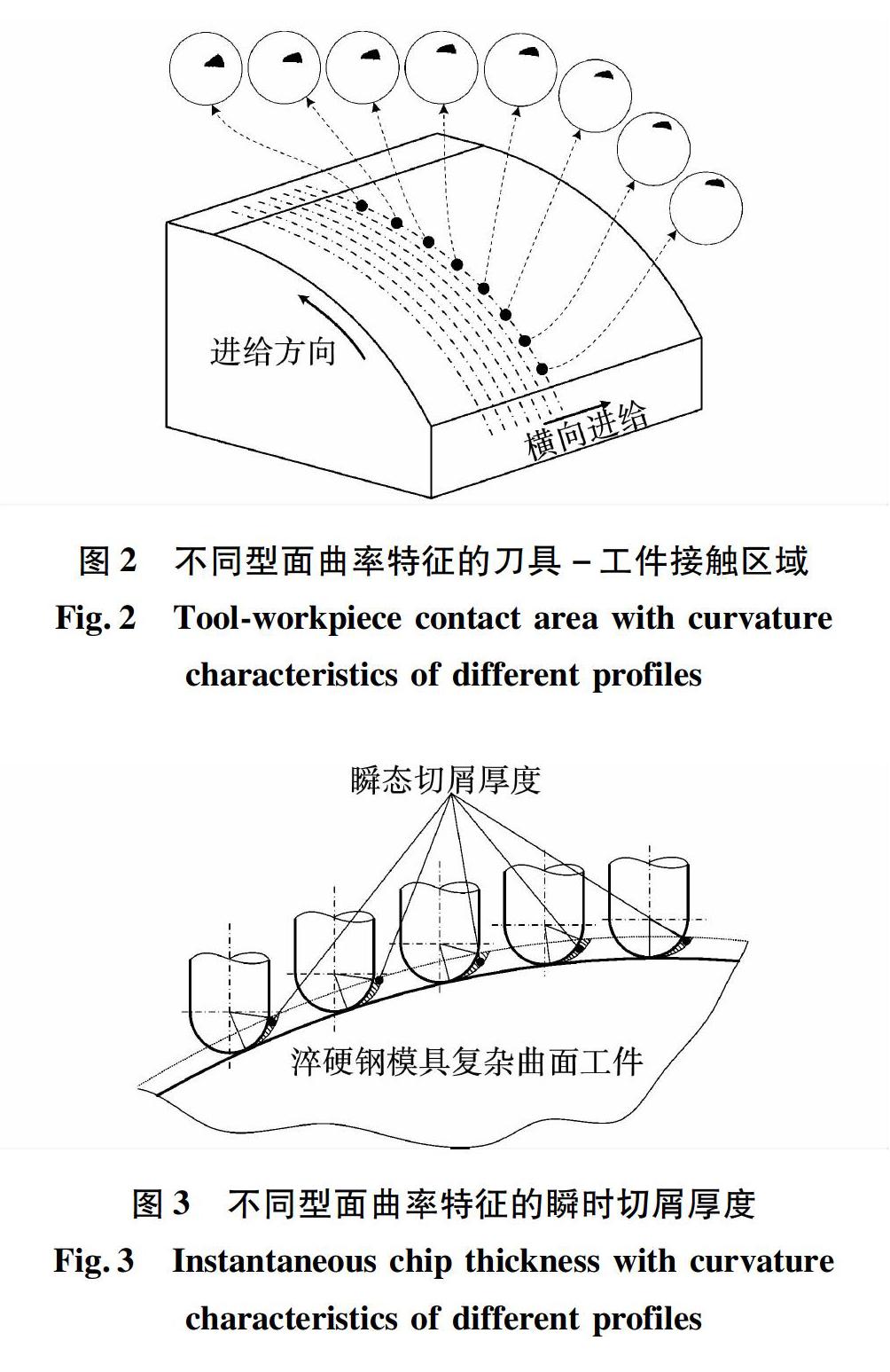
动态铣削过程主要是通过建立动态铣削力模型进行表示，淬硬钢模具具有复杂曲线曲面特征，与传统的平面铣削加工过程动力学建模是不同的，型面的曲率特征影响动态切削厚度和刀具-工件接触区域，如图2、3所示。因此，淬硬钢模具复杂曲面在建立动态铣削力模型时，刀具-工件表面接触区域提取和动态切削厚度的建模是至关重要的。

刀具-工件接触区域的提取建模的研究多在复杂曲面铣削力建模过程中，目前主要的分析方法有解析法、离散法和实体法等。解析法是通过工件表面和刀具几何尺寸直接解析计算获得刀具-工件接触区域的方法，目前有很多学者应用解析法求解刀具-工件表面接触区域，如Bailey等[15]通过确定刀刃 和工件局部表面的交线，解析计算了刀具-工件接触域;其中刀刃用NURBS曲线定义，工件局部表面用当前刀位点附近的前一个刀具轨迹生成的面定义。Ozturk和Lazoglu[16]使用刀位点数据计算得到了简单自由曲面加工时的瞬时刀具-工件接触域。Fan等[17]提出利用二次曲面对刀具进行定向并对加工宽度进行评估来获得接触区，并且利用方向角来提高加工效率。Aras[18]提出了用解析法获得刀具扫掠体的空间包络，在该种方法中，刀具的空间运动被分解为一系列的特征圆，为了获得这些特征圆，引进了球的2参数族的概念，来定义特征圆之间的关系。Lazoglu等[19]提出一种刀具路径获得方法，该方法是基于布尔运算的一种边界表示法，该方法可以获得每一个刀具位置点的复杂接触区。离散法多用于几何结构复杂的工件的刀具-工件接触域提取。这类方法中，最常用的是Z-Map方法，Z-Map方法指将工件毛坯离散为带有高度的网格点，用这些网格点描述三维曲面，仿真过程中离散网格点高度随着时间发生变化，某一瞬时变化的网格点即构成了该时刻的刀具和工件的接触区。主要研究的有G.M.Kim 等[20]提出基于Z-Map仿真模型来获得刀具-工件表面区域。魏兆成等[21]提出了一种改进的Z-Map仿真模型，该方法可以确定刀具-工件表面接触区域和瞬时切削边界。张臣等[22]基于Z-Map 仿真模型分别考虑刀具偏心和变形以及考虑剪切力和犁耕力双重效应的铣削力模型。Roth等[23]使用Z-map方法进行了五轴铣削的进给规划及静力学建模。实体法存储几何模型的点、线、面，使之成为一个等级结构。Chiou等[24]提出了一种扫掠包络法来预测五轴铣削加工过程中的刀具位置，获得了扫掠轮廓的封闭形式。Larue等[25]利用ACIS实体建模法来获得周铣加工过程中的刀具-工件接触区来预测切削力。Lazoglu等[26]对刀具、工件利用布尔运算，获取复杂自由曲面的刀具-工件接触区域。在三种常见方法的基础上，可以综合其中的两种来搭配，文[27]，采用实体法、解析法相结合的方法来获得刀具-工件接触区域，该方法，对刀具和工件进行了精确建模。在任意切削位置上进行刀具与工件之间的“布尔减法”运算，获得了可能的刀具-工件接触区域。还有Ferry等[28]采用实体法、离散法相结合的方法获取刀具-工件接触区域，该方法利用ACIS实体建模，用平行切片法获得刀具-工件接触区域。以上两种方法可以获得更好的精度和更高的效率。

目前关于铣削动力学模型建立的大量研究主要针对平面铣削过程，对于曲线曲面的铣削过程动力学已有一部分学者进行了研究。如Kardes等[29]建立了圆弧曲线铣削颤振稳定性的频域模型和数值模型，该模型考虑到了时变浸入角和方向系数，利用频域法进行求解。李忠群等[30]建立考虑再生作用的圆角曲线铣削动力学模型，通过几何分析将直线铣削颤振稳定域解析模型应用于圆角铣削的条件。郝红艳等[31]基于直线插补给出了刀具位置角、进给方向角及加工时间的确定方法。考虑偏心跳动对未变形切削厚度的影响，建立了变曲率曲线铣削动力学模型。文[32]考虑淬硬钢模具拐角处铣削加工切削厚度的变化，建立拐角处的瞬时铣削力模型。以上研究主要针对曲线的铣削加工过程，建模过程中重点研究了曲线铣削加工刀具的切入角和切出角，并作为铣削动力学模型的边界条件。文[33]针对淬硬钢模具自由曲面铣削加工，提出了一种对切削刃离散微元取加权平均值的瞬时未变形切屑厚度预报方法，建立了考虑自由曲面曲率和前倾角对未变形切屑厚度和时滞参数影响的变时滞动力学模型。文[34]考虑淬硬钢模具复杂曲面工件铣削加工的不同位置的刀具-工件表面接触区域不同，建立复杂曲面的铣削动力学模型。

综上所述，淬硬钢模具复杂曲面铣削过程多为变时滞、变参数铣削加工，考虑模具型面特征、铣削条件和刀具参数等因素，准确建立动态铣削力模型、铣削过程模型是研究的关键，目前该方面的理论需要进一步深入研究。

3 铣削过程稳定性分析研究现状

目前求解铣削加工稳定域的方法可以大体分为颤振模型求解法和实验法两类。实验法是通过变切削深度的方法，通过分析切削振动信号识别极限切削深度，从而得到稳定性极限图。如Twardowski[35]针对淬硬钢铣削加工，选用不同的切削参数，通过测量颤振加速度信号以及测量铣削力进行稳定性判定。刘安民等[36]提出了一种使用测量加工过程中的噪声来诊断高速铣削颤振的方法，通过建立的数学模型和测量的加工噪声来求解工艺系统固有频率、阻尼比和过程参数，进而计算出稳定域极限。石莉等[37]则通过对测量的铣削力进行小波分析来重构动态铣削力，利用动态铣削力的变化来对铣削颤振进行预测。该方法虽然简单、方便，但是不具备一般性。颤振模型求解法又可分为频域法和时域法。频域法通常运用傅立叶变换将切削加工的时滞微分方程组转换到频域表示，随后基于控制理论求解铣削稳定边界。Altintas等[38]率先提出了零阶求解法，之后利用该方法进行球头铣刀的铣削稳定性分析。Merdol等[39]在考虑定向因子高次谐波的前提下提出了多频率法，该方法由于需要迭代搜索颤振频率，需求解多个特征值。Bachrathy等[40]把多频率法进行了扩展，扩展后的多频率法可以适用于不同刀具几何结构的切削加工稳定性预测。时域法是在时间域内对铣削过程稳定性进行分析、仿真的方法，分为半离散法和全离散法。Insperger等[41]提出的半離散法，将动力学方程中的时滞项和系数项进行离散化，划分为若干个常微分方程来逼近原来的方程，并保持误差的收敛性，当离散数越多时，计算精度越高。龙新华等[42-43]用半离散法分析了考虑刀齿跳出效应的多时滞铣削过程稳定性及变转速工况的铣削稳定性。李中伟等[44]提出了基于Magnus-Gaussian 截断的改进半离散法。宋清华等[45-46]使用半离散法分析了刀具偏心以及小径向切深下进给量对铣削稳定性的影响。Wan等[47]提出了考虑了变螺旋角、变齿间角及刀具偏心等因素导致的多延时效应的统一的半离散法。丁烨等[48]提出的全离散法突破了原有微分方程差分化的思路，这种方法从计算精度和计算效率上均使得加工稳定的预测得到了提高。文[49]针对自由曲面模具的稳定铣削，提出了一种基于时域的铣削颤振稳定性预测方法。基于数值方法计算多时滞铣削系统的振动位移，以动态切屑厚度与静态切屑厚度的比值为阈值，获得自由曲面模具铣削颤振稳定域。

可以发现频域法求解计算速度快并且精度满足大多数应用场合;时域法求解精度高，可以揭示铣削过程中蕴含的各种动力学现象、但是计算量大求解过程耗时。目前针对淬硬钢模具复杂曲面铣削稳定性预测快速、准确的求解方法的研究仍需要进一步探索研究。

4 结 论

本文主要针对淬硬钢模具铣削动力学和稳定性研究进行综述，重点归纳总结了淬硬钢模具加工系统的动态特性、淬硬钢模具复杂曲面动态加工过程建模以及铣削稳定性分析3方面的国内外研究现状，获得主要结论如下。

1）铣削加工系统动力学特性研究按照研究方法主要归纳为锤击模态试验法、导纳耦合子结构分析法以及理论分析法。且研究重点由传统的铣削加工系统静止状态下的动力学特性研究逐渐转变为考虑主轴系统在高速旋转铣削状态下的轴承刚度软化，结合面刚度软化、离心力和陀螺效应等因素影响下的铣削加工系统动力学特性。而对于淬硬钢模具铣削加工系统动力学除了应考虑以上因素，还应考虑铣削加工过程中的物理因素对铣削加工系统动力学特性的影响，而这方面的研究还不是很多，有待于进一步探索研究。

2）淬硬钢模具复杂曲面动态铣削过程模型建立的关键是动态切削厚度建模和刀具-工件表面接触区域提取，考虑模具型面特征、铣削条件和刀具参数等因素，准确建立动态铣削力模型、铣削过程模型是研究的关键，目前该方面的理论需要进一步深入研究。

3）铣削稳定性预测常见的预测方法有频域法和时域法，频域法求解计算速度快并且精度满足大多数应用场合;时域法求解精度高，可以揭示铣削过程中蕴含的各种动力学现象、但是计算量大求解过程耗时。针对淬硬钢模具复杂曲面铣削稳定性预测快速、准确的求解方法的研究仍需要进一步探索研究。

参 考 文 献：

[1] KRAJNIK P， KOPAC J. Modern Machining of Die and Mold Tools[J]. Journal of Materials Processing Technology， 2004， 20（157-158）：543.

[2] 吴石， 渠达， 刘献礼， 肖飞. 铣削过程非线性动力学的研究进展[J]. 哈尔滨理工大学学报， 2013， 18（4）：1.WU Shi， QU Da， LIU Xianli， et al. The Progress of Nonlinear Dynamics Research in Milling Process[J]. Journal of Harbin University of Science and Technology， 2013， 18（4）：1.

[3] SCHIMITZ T L， DONALDSON R R. Predicting High-Speed Machining Dynamics by Substructure Analysis[J]. Annals of the CIRP， 2000， 49（1）;303.

[4] FILIZ S， CHENG C H， Powell K B， et al. An Improved Tool-Holder Model for RCSA Tool-Point Frequency Response Prediction[J]. Precision Engineering， 2009， 33（1）;26.

[5] ALBERTELLI P， GOLETTI M， MONNO M. A New Receptance Coupling Substructure Analysis Methodology to Improve Chatter Free Cutting Conditions Prediction[J]. International Journal of Machine Tools and Manufacture， 2013， 72（3）：16.

[6] MANCISIDOR I， Urkiola A， Barcena R， et al. Receptance Coupling for Tool Point Dynamic Prediction by Fixed Boundaries Approach[J]. International Journal of Machine Tools and Manufacture， 2014， 78（1）：18.

[7] AHIN O， ALTINTAS Y. Prediction of Frequency Response Function（FRF） of Asymmetric Tools From the Analytical Coupling of Spindle and Beam Models of Holder and Tool[J]. International Journal of Machine Tools and Manufacture， 2015， 92：31.

[8] 趙万华， 杜超， 张俊， 等. 主轴转子系统动力学解析建模方法[J]. 机械工程学报， 2013， 49（6）：44.ZHAO Wanhua， DU Chao， ZHANG Jun， LIU Haitao. Analytical Modeling Method of Dynamics for the Spindle Rotor System[J]. Journal of Mechanical Engineering， 2013， 49（6）：44.

[9] 姜彦翠， 刘献礼， 吴石， 李茂月， 李荣义. 考虑结合面和轴向力的主轴系统动力学特性[J]. 机械工程学报， 2015， 51（19）：66.

JIANG Yancui， LIU Xianli， WU Shi， et al. Dynamics Characteristics of the Spindle System with the Interface and Axial Milling Force[J]. Journal of Mechanical Engineering， 2015， 51（19）：66.

[10]RANTATALO M， AIDANPAA J O， Goransson B， et al. Milling Machine Spindle Analysis Using FEM and Non-contact Spindle Excitation and Response Measurement[J]. International Journal of Machine Tools and Manufacture， 2007， 47（7/8）：1034.

[11]曹宏瑞， 李兵， 何正嘉. 高速主轴动力学建模及高速效应分析[J]. 振动工程学报， 2012， 25（2）;103.CAO Hongrui， LI Bing， HE Zhengjia. Dynamic modeling of high-speed spindles and analysis of high-speed Effects[J]. Journal of Vibration Engineering， 2012， 25（2）：103.

[12]曹宏瑞， 李亚敏， 何正嘉， 朱永生. 高速滚动轴承-转子系统时变轴承刚度及振动响应分析[J]. 机械工程学报， 2014， 50（15）：73.CAO Hongrui， LI Yamin， HE Zhengjia， et al. Time Varying Bearing Stiffness and Vibration Response Analysis of High Speed Rolling Bearing-rotor Systems[J]. Journal of Mechanical Engineering， 2014， 50（15）：73.

[13]CAO Y， ALTINTAS Y. Modeling of Spindle-Bearing and Machine Tool Systems for Virtual Simulation of Milling Operations[J]. International Journal of Machine Tools and Manufacture， 2007， 47（9）：1342.

[14]曹宏瑞， 何正嘉. 机床-主轴耦合系统动力学建模与模型修正[J]. 机械工程学报， 2012， 48（3）：88.CAO Hongrui， HE Zhengjia. Dynamic Modeling and Model Updating of Coupled Systems between Machine Tool and Its Spindle[J]. Journal of Mechanical Engineering， 2012， 48（3）：88.

[15]BAILEY. Generic Simulation Approach for Multi-Axis Machining， Part 1： Modeling Methodology[J]. Journal of Manufacturing Science and Engineering， 2002， 124（3）：624.

[16]OZTURK B， LAZOGLU I. Machining of Free-form Surfaces. Part I： Analytical Chip Load[J]. International Journal of Machine Tools and Manufacture， 2006， 46（7）：728.

[17]FAN J H， Ball A. Quadric Method for Cutter Orientation in Five-axis Sculptured Surface Machining[J]. International Journal of Machine Tools and Manufacture， 2008， 48：788.

[18]ARAS E. Cutter-workpiece Engagement Identification in Multi-axis Milling[D]. University of Chester， 2008.

[19]LAZOGLU I， BOZ Y， Erdim H. Five-axis Milling Mechanics for Complex Free form Surfaces[J]. CIRP Annals-Manufacturing Technology， 2011， 60：117.

[20]KIM G M， CHO P J， CHU C N. Cutting Force Prediction of Sculptured Surface Ball-end Milling Using Z-map[J]. International Journal of Machine Tools and Manufacture， 2000， 40（2）：277.

[21]WEI Z C， WANG M J， CAI Y J， et al. Prediction of Cutting Force in Ball-end Milling of Sculptured Surface Using Improved Z-map[J]. Intern-ational Journal of Advanced Manufacturing Technology， 2013， 68（5/8）：1167.

[22]張臣， 周儒荣， 庄海军， 等. 基于Z-map模型的球头铣刀铣削力建模与仿真[J]. 航空学报， 2006（2）：347.

ZHANG Chen， ZHOU Rurong， ZHUANG Haijun， et al. Modeling and Simulation of Ball-end Milling Forces Based on Z-map Model[J]. Acta Aeronautica et Astronautica Sinica， 2006（2）：347.

[23]ROTH D， GRAY P， ISMAIL F， et al. Mechanistic Modelling of 5-axis Milling Using an Adaptive and Local Depth Buffer[J]. Computer-Aided Design， 2007， 39（4）：302.

[24]CHIOU J C J. Accurate Tool Position for Five-axis Ruled Surface Machining by Swept Envelope Approach[J]. Computer Aided Design， 2004， 36：967.

[25]LARUE A， ALTINTAS Y. Simulation of Flank Milling Processes[J]. International Journal of Machine Tools and Manufacture， 2005， 45：549.

[26]LAZOGLU I， BOZ Y， ERDIM H. Five-axis milling Mechanics for Complex Free form Surfaces[J]. CIRP Annals-Manufacturing Technology， 2011， 60（1）：117.

[27]JU Ganggang， SONG Qinghua， LIU Zhanqiang， et al. A Solid-Analytical-Based Method for Extracting Cutter-WorkpieceEngagementinSculpturedSurfaceMilling[J]. The International Journal of Advanced Manufacturing Technology， 2015， 80（5/8）：1297.

[28]FERRY W， Yip-HoL D. Cutter-workpiece Engage-ment Calculations by Parallel Slicing for Five-axis Flank Milling of Jet Engine Impellers[J]. Journal of Manufacturing Science and Engineering-Transactions of the ASME， 2008， 130（5）：383.

[29]KARDES N， ALTINTAS Y. Mechanics and Dynamic-s of the Circular Milling Process[J]. Journal of Manufacturing ScienceandEngineering， 2007， 129（1）：21.

[30]李忠群， 刘强. 圆角铣削颤振稳定域建模与仿真研究[J]. 机械工程学报， 2010， 46（7）：181.LI Zhongqun， LIU Qiang. Modeling and Simulation of Chatter Stability for Circular Millng[J]. Journal of Mechanical Engineering， 2010， 46（7）;181.

[31]郝洪艳， 汤文成， 王保升. 变曲率曲面周铣铣削力建模与分析[J]. 制造技术与机床， 2014（7）：118.HAO Hongyan， TANG Wencheng， WANG Baosheng. Modeling and Analysis of Milling Force in Peripheral Milling of Curved Surfacewith Variable Curvature[J]. Manufacturing Technology and Machine Tool， 2014（7）：118.

[32]季思慧， 刘献礼， 李茂月， 等. 汽车模具拐角加工铣削力建模及仿真[J]. 哈尔滨理工大学学报， 2016， 21（4）：50.JI Sihui， LIU Xianli， LI Maoyue， et al. Modeling and Simulation on Milling Forces in Automobile Mould Corner[J]. Journal of Harbin University of Science and Technology， 2016， 21（4）：50.

[33]WU Shi， YANG Lin， LIU Xianli， et al. Effects of Curvat-ure Characteristics of Sculptured Surface on Chatter Stability for Die Milling[J]. International Journal of Advanced Manufacturing Technology， 2017， 89（9/12）：1.

[34]YUE Caixu， LIU Xianli， LIANG S Y. A Model for Predicting Chatter Stability Considering Contact Characteristic between Milling Cutter and Workpiece[J]. International Journal of Advanced Manufacturing Technology， 2016， 88（5/8）：1.

[35]TWARDOWSKI P. HSM Machining Stability During Hardened Steels Milling Process[C]// ASME 2008， Biennial Conference on Engineering Systems Design and Analysis， 2008：289.

[36]劉安民， 彭程， 刘吉兆， 等. 高速铣削时颤振的诊断和稳定加工区域的预报[J]. 机械工程学报， 2007， 43（1）：164.

LIU Anmin， PENG Cheng， LIU Jizhao， et al. Detection of Chatter and Prediction of Stable Cutting Zones in High-speed Milling[J]. Journal of Mechanical Engineering， 2007， 43（1）：164.

[37]石莉， 贾春德， 孙玉龙. 应用小波研究动态铣削力及预报铣削颤振[J]. 哈尔滨工业大学学报， 2006， 38（10）：1778.

SHI li， JIA Chunde， SUN Yulong， Research on Dynamic Milling

Force with Wavelet Analysis and forecasting Milling Chatter[J]. Journal of Harbin Institute of Technology， 2006， 38（10）：1778.

[38]ALTINTAS Y， BUDAK E. Analytical Prediction of Stability Lobes in Milling[J]. CIRP Annals-Manufacturing Technology， 1995， 44（1）;357.

[39]MERDOL S D， ALTINTAS Y. Multi Frequency Solution of Chatter Stability for Low Immersion Milling[J]. Journal of Manufacturing Science and Engineering， 2004， 126（3）：459.

[40]BACHRATHY D， STEPAN G. Improved Prediction of Stability Lobes with Extended Multifrequency Solution[J]. CIRP Annals-Manufacturing Technology， 2013， 62（1）：411.

[41]INSPERGER T， STéPáN G. Semi-discretization Method for Delayed Systems[J]. International Journal for Numerical Methods in Engineering， 2002， 55（5）;503.

[42]LONG X H， BALACHANDRAN B， Mann B P. Dynamics of Milling Processes with Variable Time Delays[J]. Nonlinear Dynamics， 2007， 47（1/3）：49.

[43]LONG X H，BALACHANDRAN B. Stability Analysis for Milling Process[J]. Nonlinear Dynamics，2007，49（3）：349.

[44]李中伟， 龙新华， 孟光. 基于Magnus-Gaussian截断的铣削系统稳定性的半离散分析法[J]. 振动与冲击， 2009， 28（5）：69.LI Zhongwei， LONG Xinhua， MENG Guang. Stability Analysis of Milling Process by Semi Discretization Method Based on Magnus-Gaussian Truncation[J]. Journal of Vibration and Shock， 2009， 28（5）：69.

[45]宋清华， 艾兴， 万熠， 等. 考虑刀具偏心的变径向切深铣削稳定性研究[J]. 振动、测试与诊断， 2008， 28（3）：206.SONG Qinghua， AI Xing， WAN Yi， et al. Stability of Milling System with Variable Radial Depth of Cut Considering Runout Effect[J]. Journal of Vibration， Measurement and Diagnosis， 2008， 28（3）：206.

[46]宋清华， 艾兴， 万熠， 等. 小径向切深下进给量对铣削稳定性的影响[J]. 中国机械工程， 2008， 19（10）：1148.

SONG Qinghua， AI Xing， WAN Yi， et al. Stability Prediction for High-speed Milling Including Feed Rate in Low Radial Immersion[J]. China Mechanical Engineering， 2008， 19（10）：1148.

[47]WAN Min， ZHANG Weihong， DANG Jianwei， et al. A Unified Stability Prediction Method for Milling Process with Multiple Delays[J]. International Journal of Machine Tools and Manufacture， 2010， 50（1）： 29.

[48]DING Ye， ZHU Limin， ZHANG Xiaojian， et al. A Full-discretization Method for Prediction of Milling Stability[J]. International Journal of Machine Tools and Manufacturer， 2010， 50（5）;502.

[49]LIU Xianli， LI Rongyi， WU Shi， et al. A Prediction Method of Milling Chatter Stability for Complex Surface Mold[J]. International Journal of Advanced Manufacturing Technology， 2017， 89（9/12）：2637.

（編辑：温泽宇）