绳驱动仿人机器人下肢设计与仿真分析

王从浩，朱旭旭，刘本奇，胡小春

（合肥工业大学机械工程学院，安徽 合肥 230009）

1引言

仿人行走机器人是一类能够模仿人类形态和步行特点的机器人，具有较高的环境适应能力和广阔的工作空间，以及一定的越障能力，此外仿人机器人还可以帮助人类完成一些生活上或者极限环境下的工作，如帮助行动不便者行走，在有毒有害的工作环境中代替人类工作。因此各国都开始研制仿人机器人，迄今为止比较先进的仿人机器人主要有日本的ASIMO[1]、美国波士顿公司的Atlas[2]等。这些仿人机器人已经能够模仿人类的行走和完成一些简单的动作，但是由于这些机器人大都采用的是电机加谐波减速器安装于关节处对机器人进行驱动，不可避免的会造成机器人行走步态的僵化，与人类的自然行走步态存在较大差距。鉴于此很多学者开始探索新的关节驱动方式来解决以上问题。仿照人体肌肉-肌腱驱动方式，利用气动人工肌肉驱动关节[3]，能够实现关节的柔性驱动，但是这种驱动由于空气的可压缩性导致了驱动的不准确性。利用绳索驱动，文献[4]研制出了绳索机器人Kenzoh，该机器人只有上半身。文献[5]研制了绳驱动的仿人腿机器人，但只有两个自由度。2016年，德国达姆施塔特工业大学利用绳索串联弹簧驱动方式，设计了biobiped机器人[6]。这些机器人较电机直接驱动关节的机器人在柔顺性上有了很大的改观，但也存在着额外负载加大，关节间存在耦合关系，结构较复杂等不足。

主要研究了绳索拮抗驱动机器人，证明了绳驱动的可行性以及拉力计算的正确性。

2 绳驱动仿人下肢结构的设计

2.1 人体下肢运动机理分析

人体下肢的运动都是由肌肉肌腱带动骨骼绕关节转动产生。下肢主要有三个关节：髋关节、膝关节、踝关节。下肢有九组主要肌群，简化模型，如图1所示。股直肌3、股二头肌4和腓肠肌7都是双关节肌，能够维持下肢运动的平衡和关节运动的协调，造成双关节运动间存在复杂的耦合关系，为简化模型所以这里暂不予考虑。

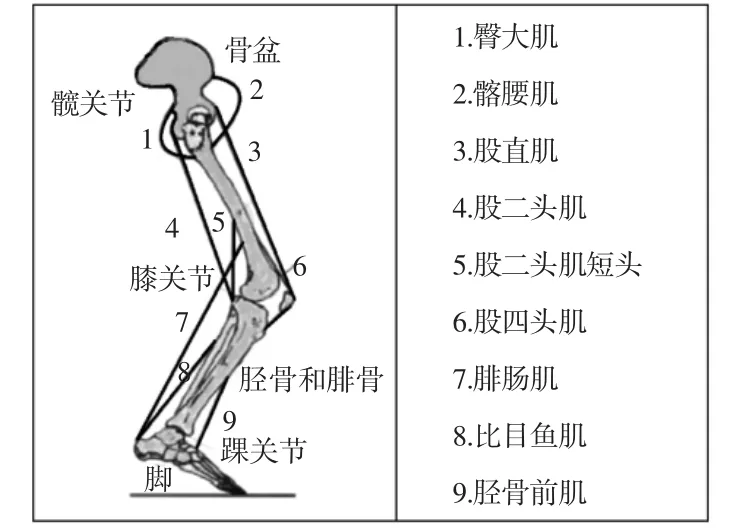
图1 下肢肌肉组成[7]Fig.1 Muscle Composition of Lower Limb

由于人体行走的运动面主要为矢状面，只研究下肢关节在矢状面内的运动情况，各关节在矢状面的运动范围，如表1所示。

表1 下肢三关节运动形式和运动范围Tab.1 The Movement form and Motion Range of Lower Extrem ity Triarthrosis

2.2 仿人下肢机器人本体设计

2.2.1 结构设计

参考人体各部分与身高的比例关系，以身高为175cm，体重60kg的人体为参考，计算得仿人下肢的大腿长度为430.5mm，小腿长度为430.5mm，踝关节距离地面的高度为68.25mm，两腿之间的宽度为340.25mm。

人在直立状态下髋关节与膝关节不在一条直线上，倾角约为10°，能够在行走的过程中增加行走的稳定性。小腿杆设计为竖直结构。将脚部设计为弓形加弹簧结构，起到减震缓冲的作用。在SolidWorks中建立机器人下肢整体模型，如图2所示。关节设计为铰链结构。机器人运动的过程中髋关节和踝关节都需要两个自由度故将这两个关节设计为虎克铰连接。人体步行的过程关节主要在矢状面内运动，需将冠状面的自由度固定。

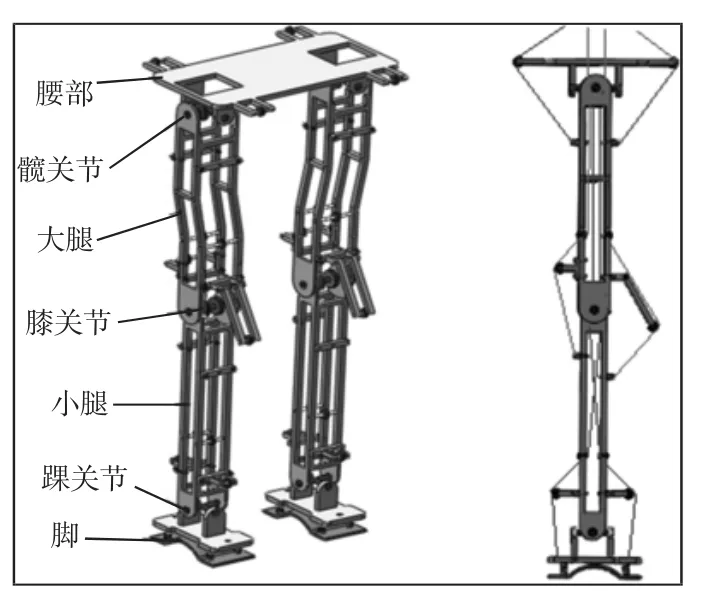
图2 仿人下肢机构三维模型Fig.2 Three-Dimensional Model of Human Lower Limb Mechanism

2.2.2 绳索和电机布置

基于绳索驱动的仿人下肢结构设计，需要考虑绳索的起止点位置和走向的布置问题，其设计原则首先是从仿生学角度，参考下肢肌肉简化模型，其次是要满足：（1）整体结构紧凑；（2）驱动力臂较大。

模型采用三对电机缠绕轮带动绳索驱动下肢三个关节。三对电机皆安装于腰部，目的是减轻额外的负载，绳索经过带有滑轮的支撑架，利用杠杆原理驱动关节。膝关节和踝关节上的绳索与髋关节存在耦合关系，导致膝关节和踝关节绳索长度变化受髋关节影响，故采用穿过关节轴的方式进行解耦，将绳索通过安装于关节轴上的滑轮将动力向下一级传动，从而解决上述耦合问题。

3 下肢关节力学及绳长分析

3.1 下肢动力学分析

将下肢简化为三连杆模型，如图3所示。建立笛卡尔坐标系，其中H、K、A表示髋关节、膝关节、踝关节，T、S、Q分别为大腿、小腿和脚的质心位置，其与关节中心的距离分别为pi。利用拉格朗日方程对该模型进行逆动力学分析。拉格朗日函数L被定义为系统动能K与势能P之差，拉格朗日方程表示的系统动力学方程式如下：

式中：M—驱动力矩；θ—广义坐标。

索绪尔认为，”语言是一个形式系统，语言表征中的施指(能指、语音形式)与所指(概念)之间是一种任意性原则结合在一起的”，[6]并没有一个在先的，有着明确边界的“现实世界”来与概念或者所指一一对应，是能指创造和构建了它的所指，而所指或概念使现实事物的边界得以明晰。德国概念史学派的历史学家科塞雷克在2006年出版的《概念史：政治社会用语的语义和语用研究》一书的导论部分指出，“(概念史)探寻由分析得出的，概念和语言之外事物的关系类型”[7]。关于“概念”的历史性问题上，科氏认为是特定时代、特定思想和事物发展之语境中生成的概念。进而关注概念在历史上的显著性，从而可以用来作为历史变迁的表征。

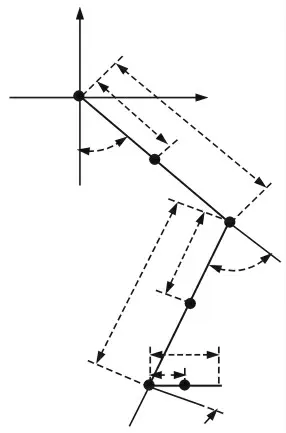
图3 下肢杆件模型Fig.3 The Lower Limb Model

选取θi（i=1，2，3）作为关节变量，mi各段杆的质量，li分别表示各段杆的长度。大小腿和脚的质心位置可以用一组坐标描述，进而求出三者的动能和势能。将上述动能和势能带入拉格朗日函数中计算得到各关节力矩与关节转角的关系如下：

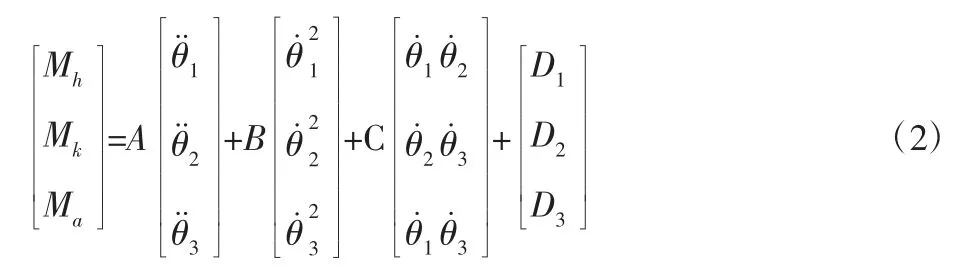
式中：Mh—髋关节；Mx—膝关节；Ma—踝关节力矩；A—惯性力矩阵；B—向心力矩阵；C—哥氏力矩阵；Di—重力矩阵。

矩阵中详细参数由于篇幅原因就不再赘述了。将一个步态周期的实验测试关节角度值[8]以及质量、转动惯量带入式（2）可求得关节力矩，下肢的质量和转动惯量，如表2所示。

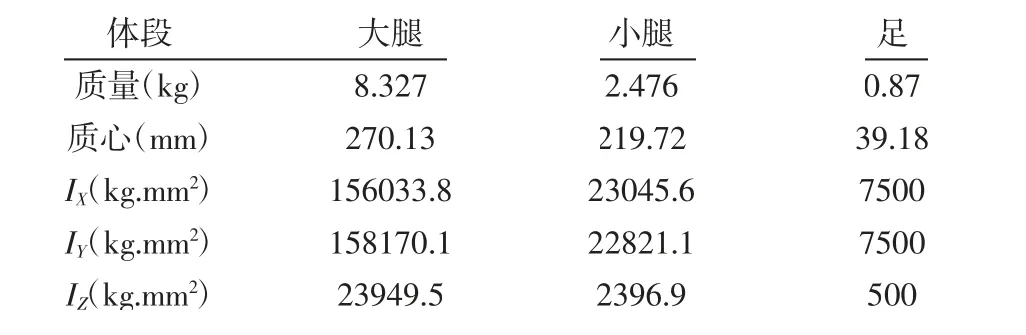
表2 下肢各部分质量和转动惯量Tab.2 The Mass and Inertia of the Lower Limbs

3.2 关节驱动绳索长度与拉力分析

该机器人的驱动方式为绳索驱动，故需要计算出关节角与两侧绳长的关系。将髋关节简化为关节模型，如图4所示。其余关节计算方法类似。

图4 关节模型Fig.4 Joint Model

以关节旋转中心为原点建立坐标系，关节转角θ以逆时针方向为正方向。xoy为基坐标系，xmmym为动坐标系，A、B点为动点，C、D、O为固定点。在初始状态下，两坐标系重合，各点在基坐标系的坐标为A（-r2，-h2）、B（r2，-h2）、C（-r1，h1）、D（r1，h1）。关节转动θ角后，动点的坐标根据坐标转换原理计算得：

式中：Lr、Ll—关节右侧和左侧的绳索长度。

电机-绳索驱动不仅需要得出绳索的长度变化规律，还需要掌握拉力的变化规律。上节已经得到机器人在运动一个步态周期各关节所需要的驱动力矩大小，由驱动关节力矩计算关节两侧驱动绳索的拉力大小，需要对关节进行动力学分析。力学分析模型，如图4所示。杆件与固定的铰链相连，两侧的驱动绳索分别通过AC、BD对杆件进行驱动，拉力大小分别为F2、F1。

式中：FC—惯性力；M—关节所需要的驱动力矩。设μi为方向与驱

动绳拉力方向相反的单位向量，将式（4）写成：

由方程可知D1×2不是方阵没有逆解，所以方程的解不唯一。此时需要通过优化的方法求出最优解。设Fmin≤F≤Fmax，绳索的拉力介于最小预紧力和最大张紧力之间。文献[9-10]提出绳拉力优化解的P-范数近似。

优化模型为：

取Fmin=10N，Fmax=500N，MATLAB仿真求出绳拉力。

4 绳驱动仿人机器人动力学仿真

4.1 绳索长度驱动和拉力驱动机器人仿真

为验证绳索长度驱动以及求得拉力的正确性，在ADAMS动力学仿真软件进行仿真分析。关节约束设置为转动副，各部分的质量和转动惯量，如表2所示。对机器人模型进行绳索驱动和拉力驱动两个仿真实验。（1）绳索驱动，利用ADAMS中的cable模块，设置绞车winch的驱动函数为绳索的变化规律，绳索的杨氏模量为1E+04MPa。（2）拉力驱动，对每个关节施加一对拮抗驱动力，驱动力的方向皆为侧上方，对每个驱动力采用Spline函数驱动，其驱动数据来自于上节求解的拉力数值。开始仿真，仿真时间分别设置为10s和1s，step步数设置为500步，仿真模型，如图5所示。仿真完成之后，利用Anglemeasure工具对下肢三关节的角度进行测量，在postcessor中观察三关节角度的变化情况。

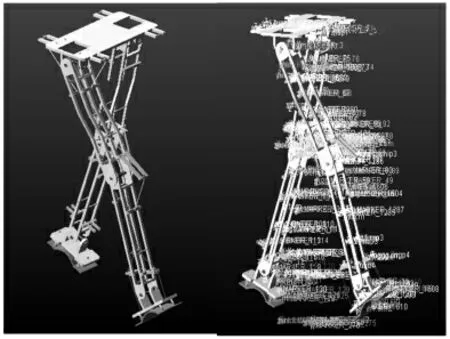
图5 仿真模型图Fig.5 Simulation Model Diagram

4.2 仿真结果分析

通过绳索驱动和拉力驱动关节的仿真实验，得出关节角的仿真值，如图5、图6所示。

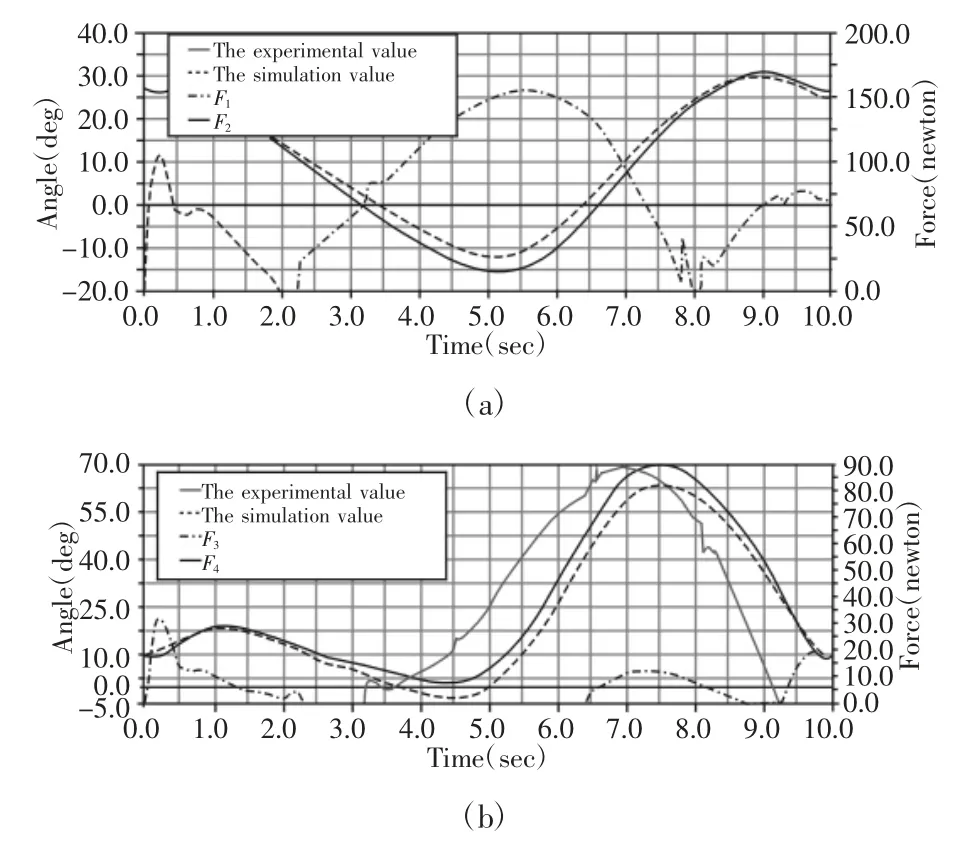
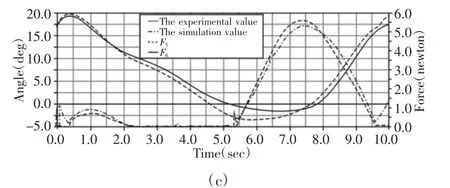
图6绳索驱动机器人仿真值与给定值对比Fig.6 The Simulation Value of the Rope Drived Robot is Compared with the Given Value

图6 中从上而下分别表示髋、膝和踝三关节的仿真结果。由图6可知绳索驱动仿真下，髋关节在后伸结束前屈开始时误差最大为2.5°，膝关节在屈腿结束伸腿开始时误差最大为8°，踝关节在跖屈最大位置时误差最大为1.7°，原因主要是绳索存在弹性变形，以及滑轮半径的影响。但总体的变化趋势是相同的，右侧纵坐标表示关节两侧绳索的拉力测量值，由此可得到绳关节运动过程中两侧绳索的拉力大小。

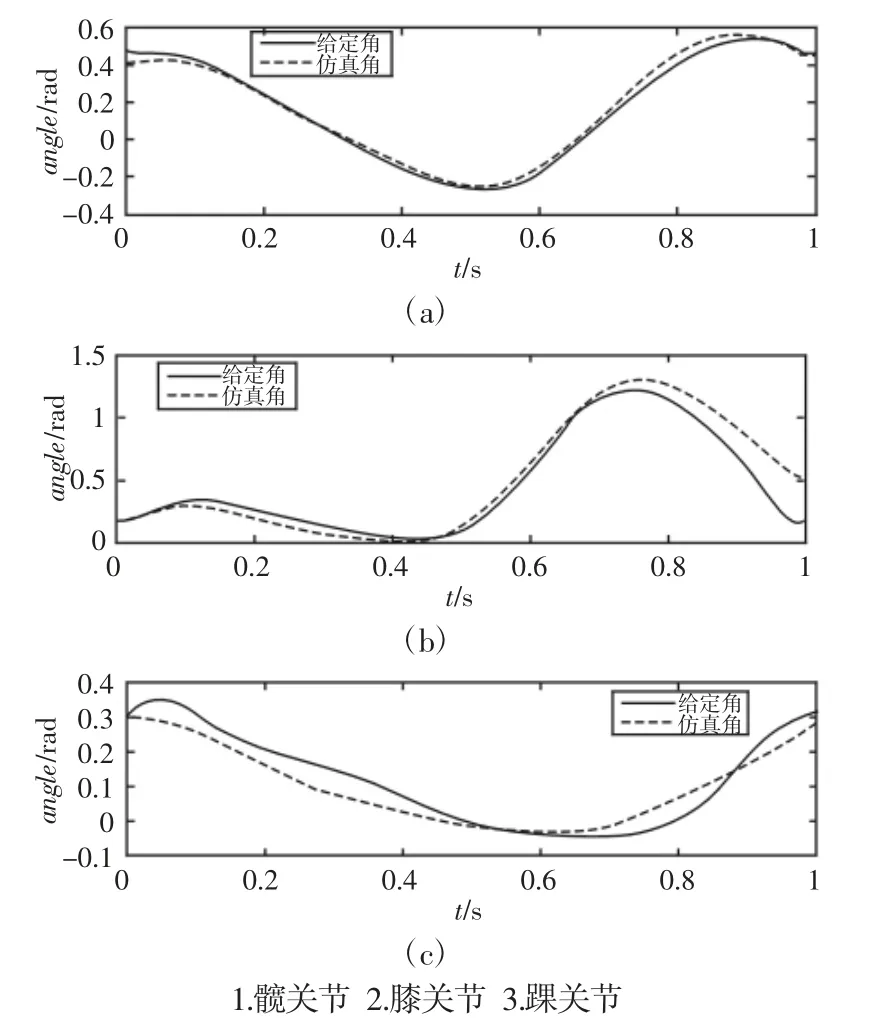
图7 拉力驱动机器人仿真角与给定角对比Fig.7 Tension Drive Robot Simulation Angle is Compared with the Given Angle

由图7可以看出，第二节计算出的拉力值能够很好的驱动相应的关节转动给定的角度，仿真值与给定值的相似度最高最大误差仅为0.033rad，如图7（a）所示。仿真值与给定值走势和极值点位置都是近似相同的，误差最大为0.31rad，，如图7（b）所示。两者存在较大的差异最大误差为0.052rad，造成这种差异的原因为关节的力矩和拉力在计算过程中存在的计算误差，如图7（c）所示。总体来说仿真结果是能够证明拉力计算结果的正确性的。

5 结论

基于绳索驱动方式对机器人下肢进行了仿生设计，利用拉格朗日方程对下肢简化模型进行了动力学分析，得到了在关节驱动力矩与关节转角的关系；利用运动学分析得到关节两侧绳长与关节角的关系，通过优化的方法得到关节两侧拉力值。仿真结果表明，绳索长度驱动产生的最大误差为膝关节8°的误差，证明了绳索长度驱动是可行的，拉力驱动的仿真值与给定值误差较大，最大为0.31rad，但总体趋势是符合的，证明了拉力计算的正确性。为下一步模型的试验打下基础。