二自由度悬索机器人运动静力学正逆解分析

任 凭，朱聪斌

（中国海洋大学工程学院，山东 青岛 266100）

1 引言

传统并联机器人机械结构复杂、工作空间受限。作为一类新型并联机构，柔索牵引并联机器人（Cable-Driven ParallelRobots）采用柔索代替刚体杆件，具有工作空间大、机械结构简单、易于模块化等优点，可应用于物料搬运、天文观测、运动模拟等领域，近年来已经成为机器人机构学研究的焦点。

柔索牵引并联机器人一般可分为悬索并联机器人（Cable-Suspended ParallelRobots）和完全约束柔索牵引并联机器人（Fully Constrained Cable-Driven ParallelRobots）两种[1]。悬索并联机器人主要依靠重力维持柔索张力，其机构自由度数一般与柔索数相同。因为柔索只能提供单向拉力，所以机器人在运动中必须维持正向拉力以保证末端执行器的稳定。这一约束条件构成了悬索并联机器人运动学、动力学与控制研究的主要难点。

悬索并联机器人的运动学理论研究主要包括空间正逆解、工作空间、轨迹规划等等[2]。在空间正逆解方面，多数研究忽略柔索质量，将其视为直线，进而采用与刚体并联机器人类似的方法进行求解[3－6]。随着大型射电望远镜FAST的成功研制[7]，考虑柔索质量的超大空间悬索并联机器人正逆解研究越来越受到重视。此类研究普遍采用悬链线方程对柔索进行建模，在运动学与静力学的耦合模型上进行求解。由于悬链线方程属超越方程，因此悬索并联机器人的正逆解无法像刚体并联机器人那样获得封闭解系，只能通过数值方法求取。近年来数值逆解方面的相关研究主要包括：文献[8]最先将悬链线方程引入了悬索并联机器人的研究，并获得了平面三自由度与空间六自由度构型的逆解。与逆解研究相比，基于悬链线模型的数值正解研究难度更大，目前相关成果较少。文献[9]采用区间分析法获得了八索六自由度冗余构型的多个有效正解，但却需要大量计算资源与时间；文献[10]求解了四索三自由度冗余构型的正解与最优逆解，但其结果无法完全满足平衡条件。目前，高效、准确的悬索并联机器人正解算法依然是一个开放性问题。

2 二自由度悬索并联机器人运动学模型

二自由度悬索并联机器人的结构，如图1所示。两台驱动缆车分别位于水平地面的A1、A2位置，两个缠绕着悬索的定滑轮分别位于同一高度上的P1和P2点，由两根等高为h的杆件支撑，杆件底端固定于地面点B1、B2。悬索长度为L1、L2。两根悬索连接于末端执行器P，末端执行器可看成是质点，质量为m。LP是两支撑杆间的水平距离，以B1B2中点为原点，建立OXZ坐标系。

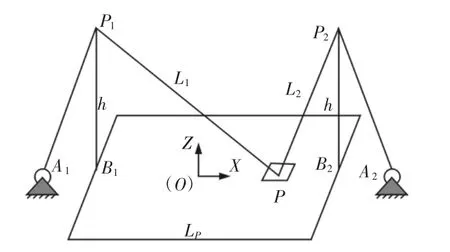
图1 二自由度悬索并联机器人的机构简图Fig.1 Schematic Diagram of a Two-D of Cable-Suspended Parallel Robot

2.1 直线模型

在忽略悬索弹性以及自身质量的情况下，可将悬索视为线性轻质连杆，此时悬索模型为直线模型。分析单条悬索的模型，如图2（a）中Lei所示。

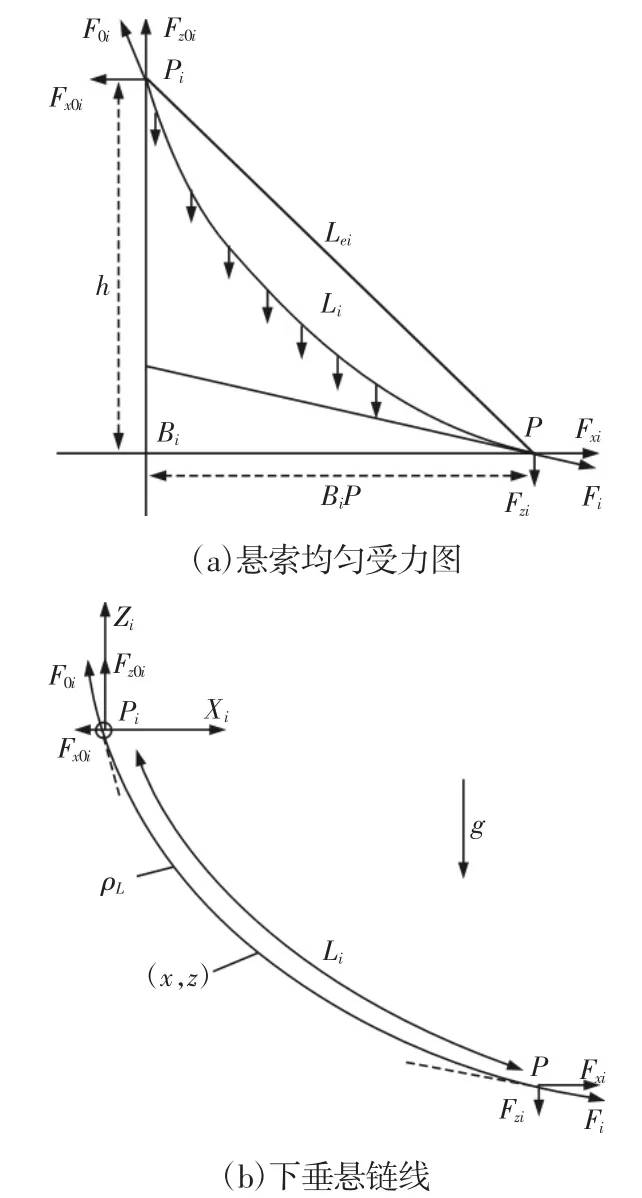
图2 悬索的悬链线模型Fig.2 Catenary Model of a Suspended Cable

在此模型中，悬索拉力Fi的方向是Pi、P两点的直线方向，并且三者符合勾股定理。

2.2 悬链线模型

若考虑悬索因自身质量产生的下垂效应，则应采用悬链线模型对悬索进行建模。单条悬索的受力情况，如图2（1）中Li所示。

假设悬索各处质量均匀分布，此时悬索不仅受末端拉力作用，而且还有自身质量产生的下垂效应，如图2所示。因此，拉力Fi的方向是悬索牵引点P处的切线方向，而不再是Pi、P两点的直线方向。

在悬链线模型中，如图2（b）所示。图中：ρL—悬索线密度；（x，z）—悬索上任一点坐标。当悬索长度不可拉伸时，悬链线方程，如式（1）、式（2）所示[7]。

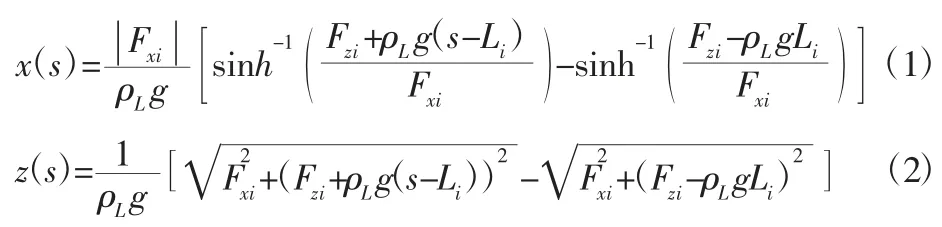
式中：s—Pi点到坐标点（x，z）的悬链线曲线长度，且0≤s≤Li。

3 二自由度悬索并联机器人运动静力学分析

3.1 静力学分析

以固定点P1和P2为原点，如图1所示。垂直向上为z1和z2坐标轴正方向，悬索向内方向为x1和x2坐标轴正方向，分别建立悬索坐标系o1x1z1、o2x2z2，如图3所示。世界坐标系OXZ的建立与图1中一致。

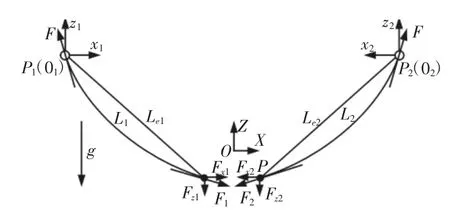
图3 悬索的悬链线模型Fig.3 Catenary Model of Two Suspended Cables

设点P在OXZ坐标系下的坐标为（Xstr，Zstr），在o1x1z1或者o2x2z2坐标系下的坐标为（Xiend，Ziend）。由图3可以得出P的位置坐标在各坐标系下的变换等式（3）。

图中：Lei—悬索在直线模型下P点到Pi点的直线距离；

Li—悬索在悬链线模型下P点到Pi点的悬链线长度；

g—重力加速度。在悬索1与悬索2坐标系下；

Fi（i=1，2）—悬索在末端执行器处所受拉力；

Fxi—拉力Fi的水平分量；

Fzi—拉力Fi的垂直分量；

Xiend、Ziend—末端执行器的位置坐标，由此可得出悬索处于静态时关于末端执行器位置的悬链线方程。

在OXZ坐标系下对末端执行器进行静力学分析，Ti（i=1，2）分别表示悬索1和悬索2对末端执行器的拉力，与Fi互为作用力与反作用力，如图4所示。图中：TxiG、TziG—悬索拉力在X轴和Z轴上的分力。静态平衡下，由图4可以推出在OXZ坐标系下的力平衡方程。再结合图3和图4，系oixizi与系OXZ之间的坐标变换，可得出Fxi、Fzi、TxiG、TziG之间的线性关系式。

图4 末端执行器静态受力分析Fig.4 Static Force Analysis of the End-Effector

3.2 运动静力学逆解分析

悬索并联机器人的运动静力学逆解是已知末端执行器在OXZ下的坐标（Xstr，Zstr）求解Fxi、Fzi、Li（i=1，2）共6个未知量的过程。首先在直线模型下求解悬索拉力、悬索长度，然后以该结果作为悬链线模型下的初值，采用数值迭代方法求解悬链线方程组。

根据前面第2节对单条悬索直线模型的分析，可以得出该平面二悬索并联机器人的机构简图，如图5所示。

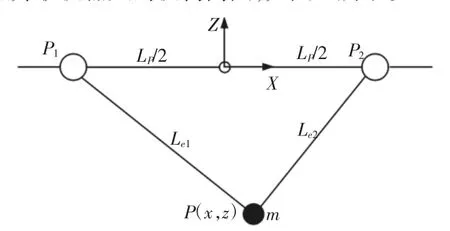
图5 平面二悬索牵引并联机器人的直线模型机构简图Fig.5 Linear Model of a Two-D of CSPR

已知P、P1、P2三点的坐标，根据图5可以得出悬索在直线模型下的长度Lei。假设Pi点的坐标为（pxi，pzi），末端执行器坐标为（x，z），则有式成立。

悬索直线模型在平衡状态下，其雅可比矩阵记作J，可表示为：

利用平衡方程，建立方程组进行悬索直线模型下拉力的求解，由图4可以推导得：

其中，T=［T1T2］T，g=［0-g］T。式（5）为以拉力大小为未知量的线性方程，求解后即可得出悬索在直线模型下的拉力向量。根据式（4）、式（5）和两悬索的静力学分析，可以得出基于悬链线模型下的运动静力学方程组（6）。其中已知量为末端执行器P在坐标系OXZ下的位置坐标Xstr与Zstr，未知量为Fx1、Fz1、L1、Fx2、Fz2、L2。这6个未知量的初值可以由悬索直线模型下的计算结果获得。

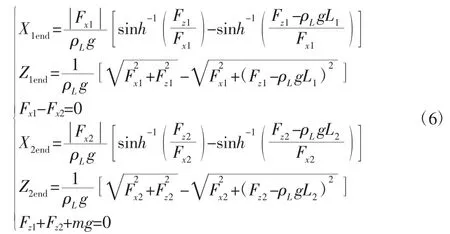
方程组（6）中，X1end、X2end、Z1end、Z2end的值，可以根据已知条件中的Xstr、Zstr与等式（3）获得。

3.3 运动静力学正解分析

运动静力学正解是运动静力学逆解的相反过程。需要以L1、L2为已知量，以Fx1，Fx2，Fz1，Fz2，Xiend，Ziend为未知量重新求解式（6）。在使用数值方法求解该非线性方程组时，同样以直线模型下获得的拉力Ti与Xiend、Ziend作为初值。

首先，将已知量L1、L2视为直线模型下的悬索长度，采用几何法求出末端执行器在OXZ下的坐标，如图6所示。

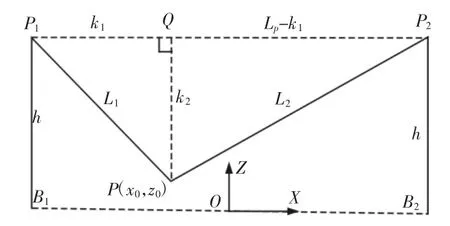
图6 直线模型下二悬索长度的几何关系图Fig.6 Geometric Relations of Two Cable Lengths Under the Linear Model

设P点坐标为（x0，z0），P1Q长度为k1，PQ长度为k2，建立一组关于k1、k2的二元二次方程。解出方程组，取正值解。再通过图6中的坐标几何关系推出P点坐标（x0，z0）。将（x0，z0）变换至悬索坐标系下，获得Xiend、Ziend（i=1，2）的初值。同时，结合式（4）、式（5）求出直线模型下的拉力，从而获得Fxi、Fzi（i=1，2）的初值。随后，由式（6）解出Xiend、Ziend，然后再通过式（3）计算出Xstr、Zstr。

4 算例仿真

4.1 模型基本参数

模型基本参数，如表1所示。

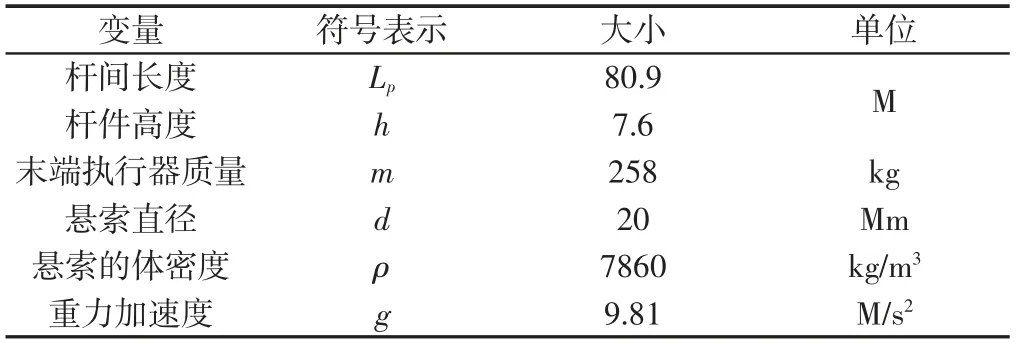
表1 模型基本参数Tab.1 Model Basic Parameters

4.2 逆解计算

在考虑末端执行器不同位置情况下的时候，设定了左、中、右三种位置情况进行仿真，三种情况的具体位置坐标为，如表2所示。

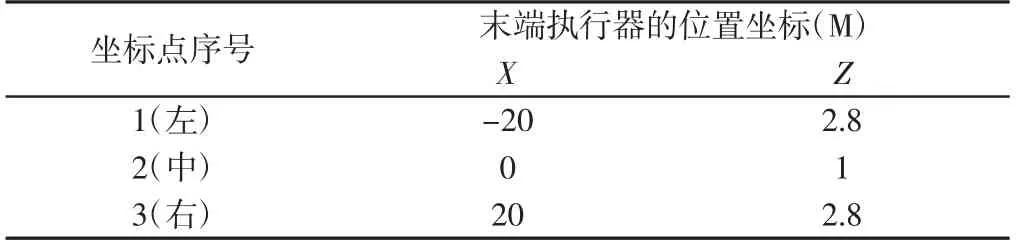
表2 末端执行器的仿真位置坐标Tab.2 The Inputposition Coordinates of the End-Effector

针对非线性悬链线方程组（6），在MATLAB程序中可使用fsolve函数求解。末端执行器P在3个不同坐标情况下的逆解结果，如表3所示。其中，程序运行平均耗时为0.8s。

表3 运动静力学逆解仿真结果Tab.3 Simulation Results of the Inverse Kinetostatics

4.3 正解计算

运动静力学正解的仿真验证过程是以逆解所求的悬索长度为已知条件，计算出末端执行器P的坐标、悬索拉力等6个未知量。悬索悬链线模型下未知量的初值选取，同样以直线模型下的悬索拉力Ti、与Xiend、Ziend坐标为初值。末端执行器P在3个不同坐标情况下的正解结果，如表4所示。其中，程序运行平均耗时为0.9s。对比表（3）、表（4），正、逆解结果一致，得到了预期中的统一结果。

表4 运动学正解仿真结果Tab.4 Simulation Results of the Forward Kinetostatics

4.4 悬链线模型简图

根据2.1节中的图2（2），以及式（1）、式（2）。如果已知s的大小，即可求出末端执行器P的坐标。其中，s表示Pi点到P坐标（x，z）的悬链线曲线长度。综合4.2中已经求出的运动学逆解结果，将Fxi、Fzi、Li代入式（1）、式（2）中，得出x、z关于变量s的函数。再由变量s的x、z函数，可以由仿真绘制出末端执行器在不同位置情况下的悬链线模型，如图7所示。

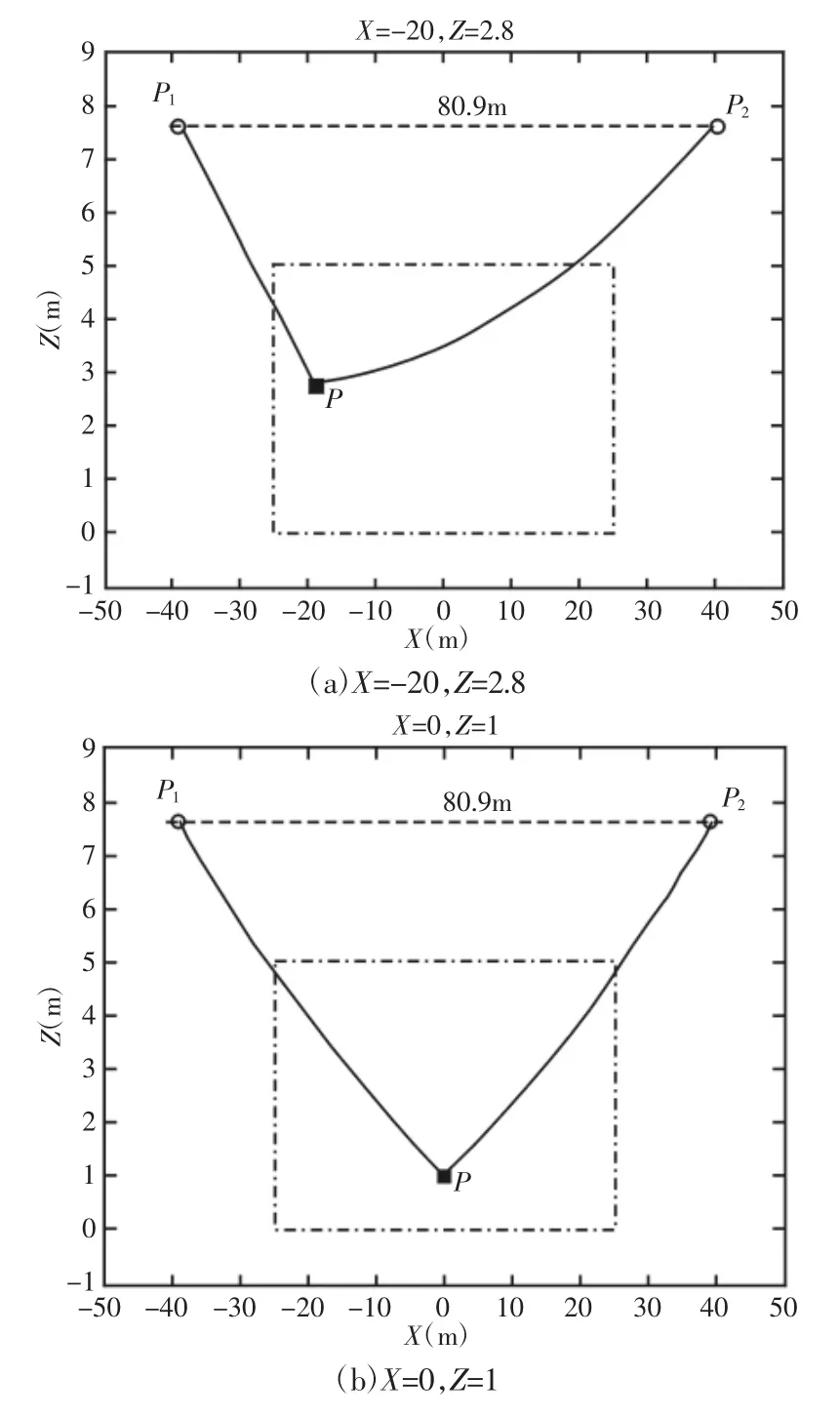
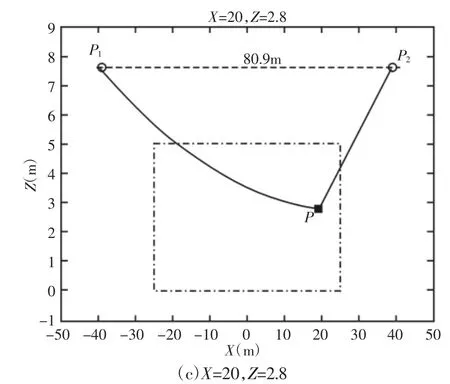
图7 平面2-DOF悬索并联机器人的悬链线模型Fig.7 Catenary Model of Planar 2-DOF CSPR

由图7可知，结果符合悬链线模型的预期形状特征。在末端执行器的工作空间内选取子区间x∈［-25，25］，z∈［0，5］（如图7中虚线矩形所示），在此区间内选择大量不同位置坐标对仿真计算进行反复测试，结果显示该算法均能使正、逆解结果一致。

5 结论

（1）提出的方法可快速、准确地求解考虑柔索质量的二自由度悬索并联机器人运动静力学正逆解。该方法同样可以应用于三自由度、六自由度等其他悬索并联机器人。（2）大量仿真算例验证了该方法能够获得稳定的唯一正逆解，在实际应用中，可以为柔索长度提供准确的期望输入。