基于多属性群决策驾驶室人机工程评价分析

丁传锋

（郑州科技学院，河南 郑州 450000）

1 引言

工程车辆驾驶员操作环境较为恶劣，舒适性相对较差，驾驶室需要为驾驶员提供良好舒适操作环境，既可减少劳动者疲劳损伤，又可减少机械人为故障[1]。具备良好人机工程环境的驾驶室，可以使得驾驶员保持长时间的注意力，因此，对驾驶室进行人机工程学分析，具有重要的意义。国内外学者对此进研究：文献[2]基于工程实践统计，根据数学统计对不同驾驶室的安全性进行分析；文献[3]基于人机工程理论，将人体模型与驾驶室进行数学关联建模，通过数学模型对驾驶室进行分析优化；文献[4]基于CATIA人机工程模块，对某款车辆驾驶室操作面板及控制装置进行设计布置；文献[5]基于人机工程理论，对驾驶室座椅的空间位置进行优化设计，并采用95th人体模型进行验证。

针对某工程车辆驾驶室进行人机工程学分析，根据驾驶室总体结构，搭建试验台，进行人机工程学试验。选取20名相关专业人员，从四大类进行操作评价，反映出被评判的驾驶室人机界面各方面的特点和性能，根据各子因素和相应的人机工程标准建立驾驶室评价体系。应用直觉模糊集的多属性群决策方法，综合考虑系统属性的权重和各专家的权重，对驾驶室进行人机工程评价。

2 直接模糊多属性决策

对于某一多属性群决策问题，设Y=｛Y1，Y2，…Yn｝为方案集，E=（e1，e2，…el）T为决策者集。ξ=｛ξ1，ξ2，…ξl｝T为决策者的权重向量，其中ξk≥0（k=1，2，…，l），ξk=1，G=｛G1，G2，…Gm｝为属性集，ω=｛ω1，ω2，…ωm｝T为属性的权重向量，其中，ωj∈（j=1，2，…，m），ωj=1[6]。

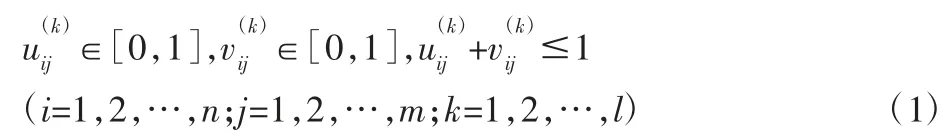
在群决策过程中，为了得到最终决策结果，需要把每个决策者提供的决策意见融合为群决策意见。为此，可利用IFHA算子：

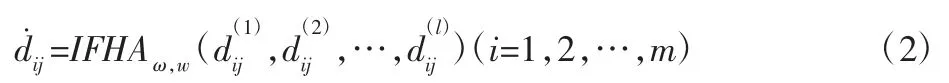
或IFHG算子：

若属性权重事先确知，即属性Gj（j=1，2，…，m），权重向量w=（w1，w2，wn，…）T，可以事先给定，则基于群的直觉模糊决策矩阵或，利用IFWA算子或（或IFWG算子）：

求得方案Yi的综合属性值。

对于任一直觉模糊数α=（αu，αv），可通过得分函数s对其进行评估：

其中s（α）为α的得分值，s（α）∈［-1，1］。

利用式（6）计算方案Yi的综合属性值d˙i或d¨i的得分值s（d˙i）或s（d¨i）（i=1，2，…，n），然后利用得分值对方案Yi进行排序并择优（如果两个得分值相等，则需要分别计算方案综合属性值d˙i或d¨i和d˙j或d¨j的精确度h（d˙i）或h（d¨i）和h（d˙j）或h（d¨j），然后利用h（d˙i）或h（d¨i）和h（d˙j）或h（d¨j）对方案Yi和Yj进行排序。

3 驾驶室人机工程试验

根据人机工程学的基本原理，针对驾驶室人机工程学研究的实际需要，研制出一台自卸车驾驶室仿真试验台。功能上，它能够模拟大多数矿用自卸车驾驶室人机关系；结构上，各部分几何位置都是可调节的[7]。试验台的总体结构，如图1所示。

图1 驾驶室结构Fig.1 Cab Structure

图中：1—仪表板支撑台，其高度可调，调节量为60mm；2—仪表板，它与竖直面的角度可通过支撑架调节，调节量为300；3—方向盘，前后左右位置可调，与竖直面的夹角可调；4—脚操作装置，包括刹车踏板和油门踏板，前后左右位置可调，与底板夹角可调，间距可调；5—手操作装置，包括变档杆和举升控制杆，前后左右位置可调，高度可调；6—座椅，安装位置可调，靠背角度、坐垫高度和坐垫倾角均可调[8]。两种布置方式的具体数据，如表1所示。

表1 两种布置方式的具体数据（mm）Tab.1 Two Specific Layout Data

两种方案的仪表和按钮的布置方式，如图1所示。

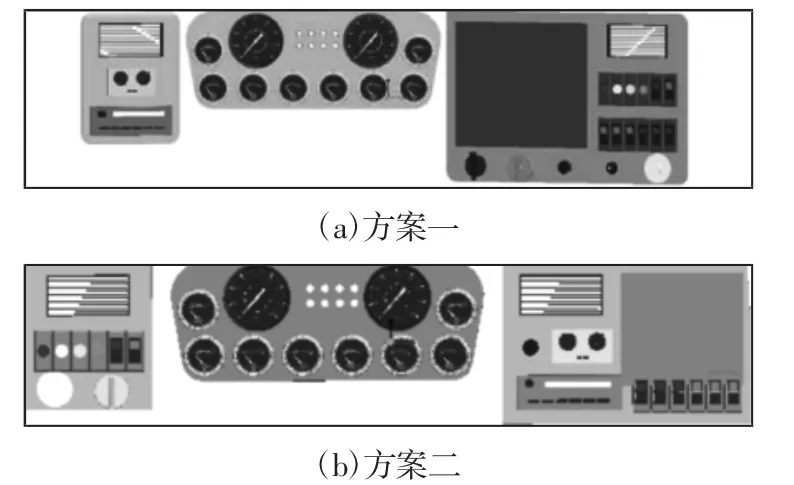
图2 仪表、按钮布置方式Fig.2 Instrument，Button Layout

试验者均为某车辆专业相关教师和学生，有驾驶经验或对汽车驾驶比较熟悉，对汽车驾驶室的内部构造比较了解[9]。共有20人参加了试验，其中教师3人，学生17人；男性17人，女性3人。试验者具体的身高分布，如图3所示。

图3 参加试验人员身高分布图（cm）Fig.3 Participate in Height Distribution of Test Personnel

根据各子因素和相应的人机工程标准建立驾驶室评价体系，如图4所示。

图4 驾驶室试验台综合评价体系Fig.4 Cab Test Bench Comprehensive Evaluation System

由于试验者包含教师和学生两种群体，这两种人群由于知识、经验和判断力有一定的差距，所以他们做出的判断的可信程度也是不同的。很显然，教师群体的评价结果应比学生的评价结果占有更大的权重。这样，因为后期处理方法不同，故对两种人群发放的调查表也不相同[10]。

4 结果评价

4.1 直觉模糊决策矩阵的提取

为方便计算，把评价项目“坐姿舒适度、仪表台、手操作装置、脚操作装置”按照图4的对应关系分别记为“Zi、Yi、Si、Ji”；把两种方案分别记为“F1、F2”。

（1）学生用调查表直觉模糊决策矩阵的提取

参与试验学生的知识水平、实际经验基本相同，对本次试验的认知程度相同，故认为他们的权重相同。所得直觉模糊决策矩阵，如表2所示。

表2 直觉模糊决策矩阵D1Tab.2 Intuitionistic Fuzzy Decision Matrices D1

其中，d22=（0.5，0.3）是在第二组调查的20份表中，“坐垫高度”指标“满意”得票10张，“不满意”得票6张，“不确定”得票4张。按直觉模糊集定义，μF2（Z2）=10/20=0.5，vF2（Z2）=6/20=0.3。而4张“不确定”票视为犹豫票，从而犹豫度为πF2（Z2）=4/20=0.2。

（2）教师用调查表直觉模糊决策矩阵的提取

教师的直觉模糊决策矩阵，如表3所示。

表3 直觉模糊决策矩阵D2、D3、D4Tab.3 Intuitionistic Fuzzy Decision Matrices D2、D3、D4

4.2 三个权重确定

4.2.1 评价因素权重确定

根据以上分析，取坐姿舒适度、仪表台、手操作装置和脚操作装置在第一层中的权重向量为ω=（0.35，0.25，0.25，0.15）T。

同理，第二层中座椅前后位置Z1、坐垫高度Z2、靠背倾角Z3、肩/腰部支撑Z4、坐垫倾角Z5在坐姿舒适度Zi中的权重向量为ωZ=（0.3，0.15，0.25，0.2，0.1）T；膝部空间Y1、仪表板相对安装位置Y2、仪表板板面倾角Y3、仪表布置Y4、仪表与方向盘的视觉盲区Y5、操作按钮位置逻辑性Y6在仪表台Yi中的权重向量为ωY=（0.25，0.1，0.1，0.15，0.2，0.2）T；方向盘的大小S1、方向盘安装角度S2、换档杆高度S3、换档操纵力的大小S4、举升器手柄的高度S5、举升器操纵力的大小S6、按钮操作舒适度S7在手操作装置Si中的权重向量为ωS=（0.15，0.2，0.15，0.1，0.15，0.1，0.15）T；踏板的相对位置J1、踏板间隔J2、踏板防滑性J3在脚操作装置Ji中的权重为ωJ=（0.4，0.4，0.2）T。

第二层中各项因素在总体系中的权重等于其在第二层种所占权重乘以它的上级项目在第一层中的权重，用ω表示。则：

4.2.2 评价者权重确定

将学生群体视为一个整体，赋予它一个权重，与三名教师并列一起。则｛学生群，教师1，教师2，教师3｝的权重向量为ξ=（0.1，0.4，0.3，0.2）T。

首先利用IFHA算子式（4）把每个直觉模糊决策矩阵Dk=

表4 群直觉模糊决策矩阵DTab.4 Group Intuitionistic Fuzzy Decision Matrix D

基于群直觉模糊决策矩阵D，利用IFWA算子得到方案Fi（i=1，2）综合属性值di（i=1，2）：

计算两个方案的得分值s（di）（i=1，2）：

s（d1）=0.732-0=0.732，s（d2）=0.596-0=0.596因此，s（d1）＞s（d2），从而最佳方案为F1。

4.3 结果数据分析

在两种排布方案中得分都很低的项目是：肩/腰部支撑和仪表与方向盘视觉干涉两项。对于前一点，通过加强腰部支撑解决。对于仪表与方向盘视觉干涉，将计时表去掉，把计时功能集成到发动机转速表上，并将仪表重新排列。修改前后仪表排布方式，如图5所示。对于第一种座椅安装位置（Hx=（580～700）mm，Hy=（400～440）mm），如图6所示。不仅能满足身材较高的人群，而且能满足身材较矮的人群；而对于第二种座椅安装位置（Hx=（530～650）mm，Hy=（360～400）mm），能满足身材较矮的人群，不能满足身材较高的人群，所以在第二组中部分调查表的“座椅前后位置”选项得分较低。

图5 仪表排布方式Fig.5 Instrument Arrangement

图6 试验者对两种座椅布置方案的满意度Fig.6 Satisfaction with the Two Seating Arrangements

5 结论

应用直觉模糊集的多属性群决策方法，综合考虑系统属性的权重和各专家的权重，对驾驶室人机工程进行分析，结果可知：（1）座椅部分得分的高低直接影响到整个驾驶室内部的得分值，直接影响驾驶室人机工程评价结果，故在设计中应首先考虑座椅的布置问题。（2）所研究驾驶室得分都很低项目：肩/腰部支撑和仪表与方向盘视觉干涉两项。前者通过加强腰部支撑解决；对于后者决定将计时表去掉，把计时功能集成到发动机转速表上，并将仪表重新排列，可以看到，修改后的仪表盘上所有仪表都位于视野内，不存在盲区。（3）对于座椅位置的两种布置方案，第一种座椅安装位置表现更优越，不仅能满足身材较高的人群，而且能满足身材较矮的人群，可以作为设计方案。