研磨参数对等高齿研磨质量的影响研究

周廷美，刘 敏，莫易敏，谢熊亮

（武汉理工大学机电工程学院，湖北 武汉 430070）

1 引言

螺旋锥齿轮加工工序大致分为毛坯切齿、渗碳热处理、修形研磨三大块，由于等高齿准双曲面齿轮经热处理加工后为硬齿面，无法通过磨齿加工改善齿面质量，因此只有采用研磨的方式修正热处理齿形。齿轮研磨是以机床设定的V/H研磨路径为前提，在合理的研磨机床参数和良好的研磨剂条件下，利用磨料颗粒与金属表面的相对运动剔除齿面局部余量，改善齿轮表面粗糙度和接触区的质量。文献[1]通过建立数学模型分析了机床运动误差和齿轮副安装误差对研齿工艺的影响，提出了基于ETCA的研磨技术比基于TCA的更合理的观点。文献[2]分析安装误差与安装工艺参数之间的关系，制定了更合理的研磨机床参数。文献[4]运用田口法对减速器进行稳健性分析，结合了模糊评判法评价了稳健性设计的参数优化组合。文献[6]研究了转速和载荷对齿轮啮合及噪声的影响，提出了研齿对齿轮副动态性能的影响作用。

实际上，合理的研齿工艺参数能降低机床运动误差和安装误差对研齿质量影响。基于上述理由，利用田口方法对螺旋锥齿轮的研齿工艺参数进行参数设计，分析各参数对齿面粗糙度影响力，找出最优参数组合，达到改善齿轮研磨质量的目的。

2 研磨参数对等高齿研齿质量的影响

经过对奥制等高齿加工工艺的理论研究和研磨后齿轮接触区质量的分析，发现研磨工况中加载力矩、齿侧间隙、主轴速度对齿轮研磨的接触区质量和一致性，以及齿面粗糙度有显著影响。等高齿准双曲面齿轮副啮合原理，如图1所示。n1为主轴输入转速，ΔV/ΔH/ΔG为齿轮副安装误差，通过预先在机床界面中设定工艺参数，调整主被轮齿从零侧隙缓慢退至图中理论侧隙的位置进行研齿。但因为存在工装精度误差、安装误差等因素，理论的机床参数值并非等同于实际的安装值，因此有必要对研磨工况进行参数优化以补偿不可控误差，优化研齿工艺。

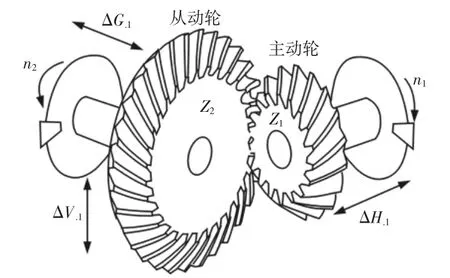
图1 等高齿准双曲面齿轮副啮合原理图Fig.1 Contour Tooth Hypoid Gear Meshing Principle Diagram

格里森600HTL研齿机结构，如图2所示。600HTL数控研齿机的人工操作界面，如图3所示。从研齿理论与产品质量分析发现主轴输入转速的大小影响齿轮研磨质量的好坏，速度过大容易引起研磨剂飞溅，研磨介质无法停留在齿面进行研磨，且在同一研磨时间下，主轴转速越快，主齿研磨时间则越长，更易引起齿面的研伤；齿侧间隙的设定与研磨剂中磨料颗粒的大小和齿轮的传递误差TE（Transmissionerror）紧密相关，侧隙过小，接触齿面摩擦发热产生齿面烧伤、胶合的现象，侧隙过大，齿轮传动不平稳，震动过大引发噪声；制动力矩的大小与齿轮接触印痕有直接关系，力矩过大，会造成齿轮对滚接触区变大，甚至占据全齿面，不利于试验分析且易造成齿面磨损，力矩过小，接触印痕过浅，不利于质量分析。因此依据上述理由，利用田口方法对加载力矩、齿侧间隙、主轴转速进行稳健性参数设计，利用正交表设计三因素三水平的试验，找出各因素对研齿质量的影响顺序，选出最优参数组合使输出变差最小，以降低齿面粗糙、提高研磨后齿面接触区质量和一致性。

图2 格里森600HTL数控研齿机Fig.2 Gleason 600HTL CNC Gear Grinding Machine

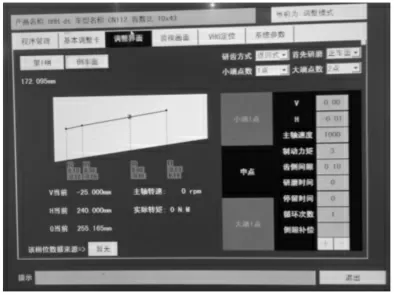
图3 格里森600HTL数控研齿机操作界面Fig.3 Gleason 600HTL CNC Gear Grinding Machine User Interface

3 田口方法参数设计

3.1 田口稳健性设计基本理论

稳健性[3]（Robustness）就是产品的机能特性不易受噪声因子差异的影响，其中的噪声因子是使产品质量偏离目标值的干扰因素。文献[4]通过将稳健性设计到产品和制程中去来提高产品质量特性对抗干扰的能力，运用正交表对产品进行稳健性参数设计，通过少数几次运行便可对多因子相互独立的分析，计算出因子影响力的大小顺序及使响应变异最小化的因子设置，以使制造出成本最低、变异最小的产品。信噪比SNR（Signal-Noise ratio），大致可理解为产品制造时控制质量的参数信号与使产品质量变异的不可控噪音信号的比值，与成本有着密切的关系，其值越大表示产品给社会产生损失越小，质量性能越好。根据质量特征值目标值的不同可分为三种形式：望大型、望目型、望小型。对于评价等高齿锥齿轮的研磨效果，研后齿面粗糙度值越小，效果越好，又试验结果Rsk始终为负值，根据质量特征值非负的特性，则取质量特征值y=－Rsk，y值越大越好，这种使响应最大化的特征符合望大特性信噪比。该情况下S/N值（信噪比）公式为：

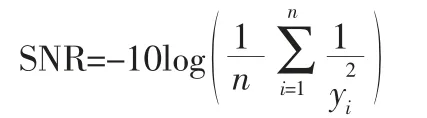
式中：n—各组对应试验次数；yi—各实验对应的质量特征值。

3.2 田口设计—正交表

3.2.1 确定试验因子

将影响研齿表面粗糙度的因子可分为可控与不易控两类，由上述分析可知，主轴速度A、制动力矩B、齿侧间隙C对等高齿锥齿轮研磨质量的影响显著，且三者之间几乎无交互作用属于可控因子类；但齿轮材料M、工装精度N、研磨剂类型P这三类在制造过程中难把控，所以将其归为噪声因子。

3.2.2 正交表

各研究因素选取的因子水平，如表1、表2所示。运用Minitab软件建立正交表，选取L9（34）为正交表的外表、L4（23）为内表，可知A～C为可控因子，M～P为噪声因子。对试验数据进行信噪比[7]分析，找出使输出变差最小的组合参数，并用数控研齿机进行检验。Minitab创建的正交表的内表，如表3所示。

表1 控制因子及水平Tab.1 Control Factors and Levels

表2 噪声因子及水平Tab.2 Noise Factor and Levels

表3 正交试验的内表Tab.3 Orthogonal Experiment in the Table

3.2.3 试验结果分析

Minitab基于Delta值分配秩，秩表示各因子的最佳水平，Delta值越大，秩越靠前，如表4所示。可知对信噪比值的影响顺序为：主轴转速＞齿侧间隙＞制动力矩，且从Delta值占比来看，转速与侧隙占比大，说明通过调节转速和侧隙对研齿效果更明显。信噪比主效应图可知当主轴转速为1800r/min、制动力矩为3.5N、齿侧间隙为0.09mm时，信噪比值均最大，而SNR值越大说明产品性能越好，所以试验最优组合为A2B2C2，如图4所示。

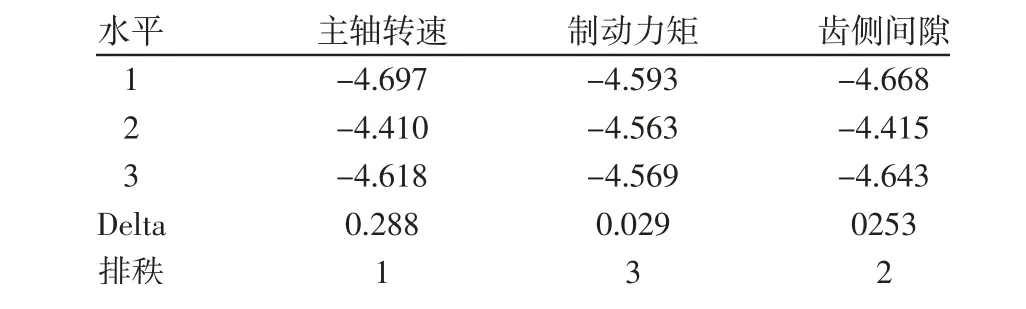
表4 信噪比响应表Tab.4 Signal to Noise Ratio Response Table

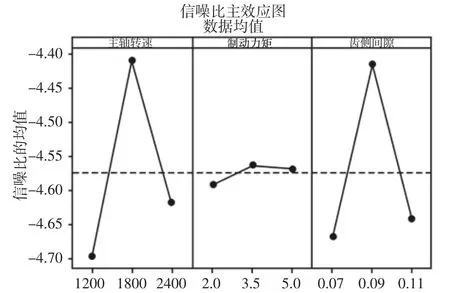
图4 信噪比主效应图Fig.4 SNR Main Effect Map

4 试验结果验证

将9组正交试验参数组合用于格里森600HTL数控研齿机进行研齿实验验证，每组参数选取3套奥制等高齿进行加工，并对研后27套齿轮副用粗糙度检测仪一一进行表面粗糙度检测，齿轮粗糙度的测量，如图5所示。齿轮副凹凸面粗糙度检测值，如表5所示。其中（19～21）为水平组合为A2B2C2时的试验齿轮副，不难看出在27对齿轮副中其粗糙度值普遍偏小、一致性良好，并且达到研后齿面粗糙度设定的标准。但为进一步验证最优水平组合的合理性，利用600HTT滚动检查机检测研磨后齿轮副的传递误差SFT值，并对其作极差分析，如图6所示。27套齿轮配对检测SFT值变化量，如表6所示。SFT的极差分析表，如表7、表8所示。由因素的K值和极差R值分析可得影响Rsk值因素的主次顺序为：主齿转速A＞齿侧间隙C＞制动力矩B，最优水平组合为A2B2C2，与利用参数设计寻优的结论基本一致，进一步验证了试验模型的准确性。

图5 齿面粗糙度测量Fig.5 27 Testing Tooth Surface Roughness

图6 600HTT滚齿机Fig.6 600HTT Gear Hobbing Machine

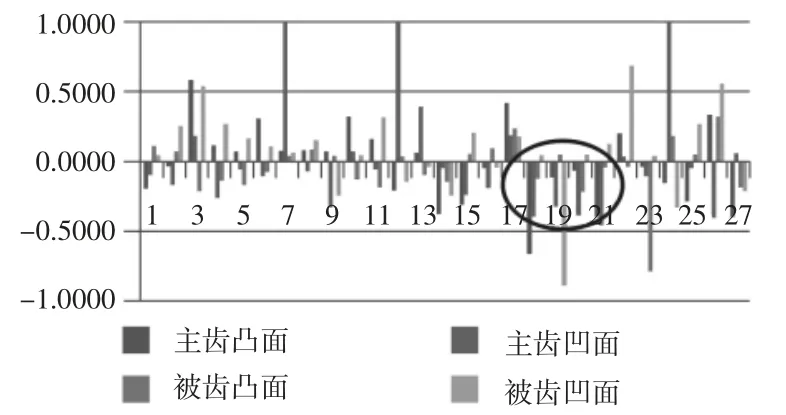
图7 27套齿轮倒车面粗糙度值Fig.7 27 Sets of Gear Reverse Surface Roughness Value

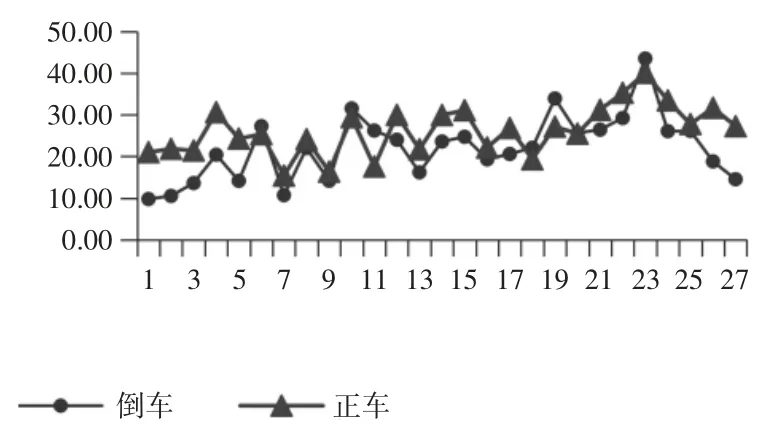
图8 SFT变化量Fig.8 SFT Variation

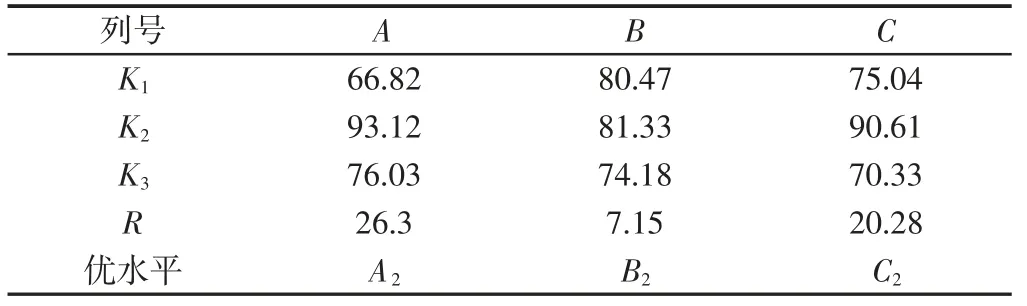
表5 正车面极差分析表Tab.5 Positive Car Surface Analysis of Poor Range Table

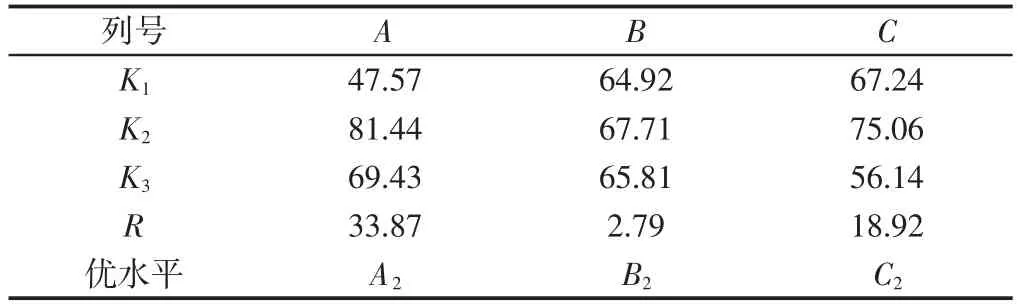
表6 倒车面极差分析表Tab.6 Reverse Car Surface Analysis of Poor Range Table

5 结论

利用田口方法对等高齿准双曲面齿轮的研磨工艺进行稳健性参数设计，分析主轴转速、制动力矩、齿侧间隙对研磨后齿轮表面粗糙度的影响，设计最优的水平组合，并将正交表中各水平组合用于Gleason研齿机进行实验验证，通过对比分析研磨后的齿轮的传递误差SFT值和粗糙度Rsk值，验证了田口法参数设计与实际试验的结果基本一致。

（1）研磨参数对研后齿轮表面的光滑度有显著的影响，影响深度：主轴转速＞齿侧间隙＞制动力矩。（2）在参数试验的水平范围内，最优组合为：主轴转速为1800r/min、制动力矩为3.5N、齿侧间隙为0.09mm。（3）将理论性的参数优化设计与实际制造实验相结合，提高试验结论的准确性，为等高齿准双曲面齿轮的研齿工艺提供了理论依据和技术指导，达到改善齿面接触区质量、提高齿轮啮合平顺性的目的。