计及全寿命周期成本的主变压器检修方案研究

马松龄，王 亢

（西安建筑科技大学机电工程学院，陕西 西安 710055）

1 引言

主变压器作为电网运行的主设备之一，它的可靠运行很大程度上影响到电网的稳定程度。为了降低因主变压器故障概率攀升而导致的电网停电风险，需要定期展开检修工作。检修工作时制定合理检修策略，不仅能有效消除主变压器部件缺陷，降低主变压器故障概率，还能有效降低（30～60）%高昂的检修维护成本[1-2]。

制定主变压器检修策略时，应先依据相应导则进行风险评估计算，再安排检修计划，该方法主要从技术角度评估风险等级，计算比较繁琐，对经济指标的考量较少[3-4]。而随着技术进步，不仅对风险因子考虑更加全面，加上人工成本大幅上升，经济指标考量已不容忽视，全寿命周期成本（LCC）技术正好满足这一需求。尽管有学者进行了此方面的研究，但仍未将LCC与风险评估有效结合[5]，以提供兼顾检修风险和成本的决策方案。为此，设计了LCC与风险评估相结合的主变压器检修决策方案，建立变压器风险评估模型，分别引入缺陷指数和役龄回退因子研究检修前后变压器的故障概率及分析LCC技术在主变压器检修中的应用，并采用运筹学理论中的层次分析法（AHP）构建检修决策模型将风险值与LCC相结合，研究风险成本和经济成本在检修中的比重，权衡不同经济性和可靠性的要求，为主变压器检修决策方案提供理论依据。

2 主变压器检修总体方案

安排主变压器的检修时，首先依据南方电网公司《设备状态评价与风险评估技术导则》给出风险评估模型计算后，排定检修次序。但该导则只能计算主变压器在正常状态、注意状态、异常状态和严重状态下的4种平均故障概率，不能将每一状态评分值与故障概率关联。根据国家电网公司于2008年发布的《输变电设备风险评估导则》可以计算主变压器每一状态分值下的故障概率，但是此方法按指数拟合可能会出现设备故障概率超过100%的荒谬结果。为解决此类问题，国家电网公司在2013年颁布了企业标准Q/GDW 1903-2013输变电设备风险评估导则[6]，对计算方法有了很大改进，但由于涉及全部输变电设备，考虑因素很多，计算模型极其复杂，对于变压器检修只有指导意义，直接应用是有难度的。为与工程实际接轨，风险评估沿用南方电网公司导则，但故障概率计算采用Q/GDW 1903-2013中更为合理的方法，避免了拟合误差。

排定次序后，需要结合主变压器的LCC选择合理的检修方式，根据目前变电站主变压器运维检修的实际情况，提出三种待选检修方式（带电检修、小修和大修）。LCC是指设备在规划、设计、制造、购置、安装、运行、维护、改造、更新直到报废的整个寿命过程中所有的费用。在一个现代化管理的企业中，对于设备LCC的概念已经建立，并广泛用于招标采购、更新维护、退役处置等方面[7-8]。故采用LCC作为检修决策中的经济性指标。由于AHP在处理复杂决策问题上的实用性和有效性，最后建立AHP模型将检修后风险值和LCC有效结合，以提高检修时的经济效益为目标，将LCC技术充分运用到检修当中，提出兼顾检修风险和成本的最优决策方案。决策总体流程，如图1所示。

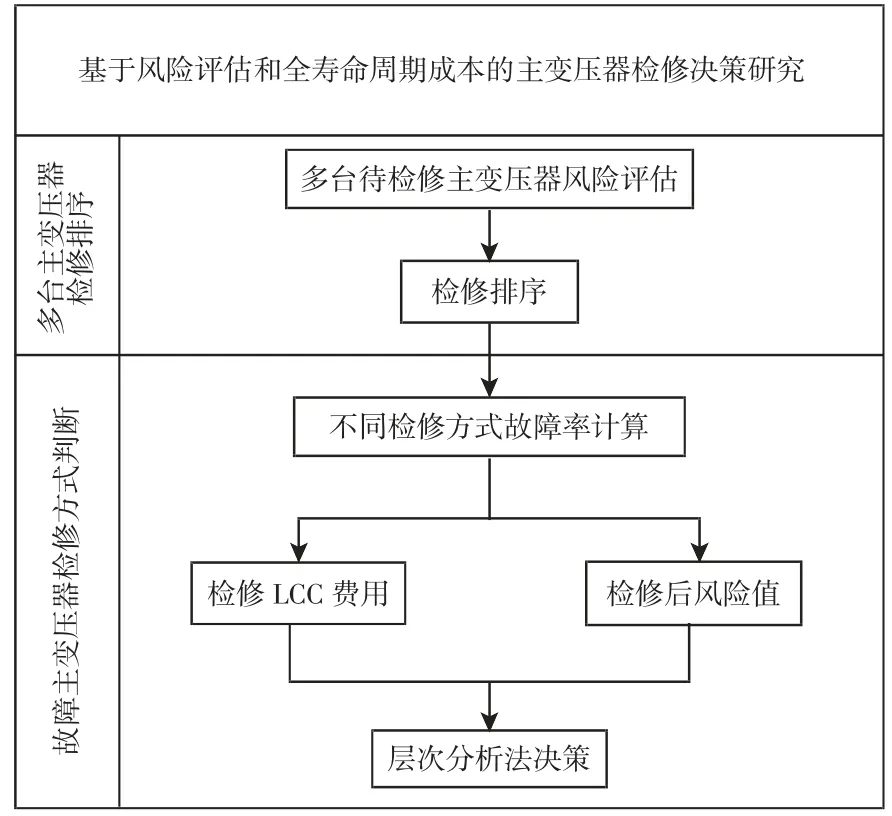
图1 检修决策流程图Fig.1 Flowchart of Maintenance Strategy

3 多台主变压器检修优先排序

依据变压器缺陷指数，计算主变压器检修前故障概率，进而实现风险评估。根据风险值决定检修次序，风险值越大的检修需求越强，从而确定优先检修顺序。

3.1 风险评估

主变压器的风险评估以风险值为指标，综合考虑可能损失的资产以及变压器故障概率二者的作用，一般来说，得到的风险值是一个无量纲量，可按式（1）计算。风险评估流程，如图2所示。

式中：t—某个时刻；R—变压器风险值；LE—可能损失的资产；P—变压器故障概率。

图2 变压器风险评估流程图Fig.2 Flowchart of Transformer Risk Assessment

3.2 可能损失的资产评估

可能损失的资产（LE）：指综合考虑资产与损失程度得到的潜在损失总量，按式（2）计算。

式中：LE—可能损失的资产；A—资产；F—资产损失程度。

变压器的资产A根据电压等级划分为三个级别，取值范围为（1～10）。具体取值时还要考虑容量的影响。变压器的资产损失程度F由成本、环境和安全三个要素的损失程度确定，每一个要素的损失程度由要素损失和要素损失概率确定。A和F的具体取值详见导则。

3.3 故障概率计算

目前国内的状态评价方法得到的设备状态分值范围约在（0～100）之间，绝大部分集中（60～100）内，2008版的《输变电设备风险评估导则》中采用指数关系来进行拟合可能会导致某一分值以下的故障率超过100%，这与实际情况并不相符。因此采用Q/GDW 1903-2013中的新方法，引入缺陷指数来计算变压器的每一状态评分值对应的故障概率。根据变压器的缺陷指数，利用以下公式来计算变压器的故障概率。

式中：d—变压器当前状态分值对应的缺陷指数；f（d）—故障率函数；P—缺陷指数为d时的变压器故障概率；A、B、C—反映变压器故障统计规律的常数，是确定故障概率的重要参数。

4 故障主变压器检修方式判断

确定多台主变压器的检修次序后，需要判断待检修主变压器的检修方式。分别计算三种待选检修方式（带电检修、小修和大修）后的故障概率、风险值及LCC费用。并依据AHP模型计算结果，确定兼顾风险和成本的最优检修决策。

4.1 不同检修方式检修后故障概率

为了确定三种待选检修方式后的风险值和LCC费用，需要对不同检修方式后的主变压器故障概率进行推算。而Q/GDW 1903-2013中提出的计算方法并未将变压器故障概率与运行时间相关联，不能直接用于检修后的故障概率预测。因此，需要对该方法加以补充，以实现检修后变压器故障概率推算[9]。检修后故障概率推算流程，如图3所示。

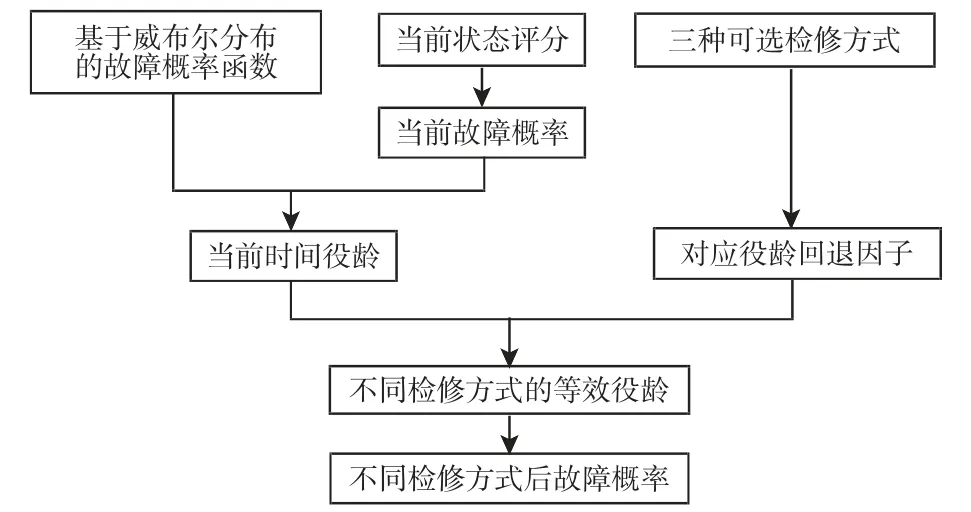
图3 检修后故障概率推算流程图Fig.3 Flowchart of Failure Rate Prediction After Maintenance

变压器故障概率与时间的变化关系曲线为经典的浴盆曲线，而通过对威布尔分布函数中参数的设定能够形象表述浴盆曲线中的早期、偶然、老化故障期，这也是变压器在全寿命周期内故障概率随时间变化的一般规律。其威布尔函数表达式，如式（4）所示。

式中：m—形状参数，无量纲，m＞0；η—尺度参数；t—变压器役龄；λ—当前设备故障概率。

采用不同检修方式，变压器的故障概率下降程度不相同。为了定量表征检修所带来变压器故障概率的变化，引入役龄回退因子α，带电检修、小修和大修的役龄回退因子分别取0.1、0.5和0.8。变压器检修后的等效役龄Teq按式（5）计算。

式中：teq—检修前实际役龄，由威布尔函数计算得到；α—役龄回退因子；Teq—检修后等效役龄。

4.2 LCC在主变压检修中的应用

对主变压器检修而言，LCC理论从经济性的角度出发，能够降低检修成本。LCC可以表达为：

式中：LCC—全寿命周期成本；CI—投资成本；CO—运行成本；CM—检修维护成本；CF—故障成本；CD—退役处置成本。

在上述表达式中，主变压器的初始投资成本CI（包括购置费、安装调试费等）、运行成本CO（包括日常巡检费用、设备能耗费用等）、退役成本CD基本是固定不变的（或不随检修方式而变动），随检修方式变化的成本主要是检修维护成本CM和故障成本CF两项。因此，在主变压器检修中主要考虑这两项成本，LCC费用计算只考虑CM和CF之和[10]。检修维护成本CM包括带电检修费用、单次小修或单次大修费用，按各电力公司统计数据取值。故障成本CF按可公式（7）计算。

式中：CF—故障成本；CF1—故障检修费用；CF2—故障损失费用；C1—现场故障修复费用；C2—停电损失费用，均根据各电力公司统计数据确定；Pafter—主变压器检修后的故障概率。

4.3 AHP在主变压器检修决策方案中的应用

AHP是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法，已经广泛应用于各个领域的决策问题当中。依据该方法对主变压器检修问题进行决策研究，具体步骤如下：

（1）建立递阶层次结构。针对检修决策问题选取适当目标层、准则层和方案层，如图4所示。

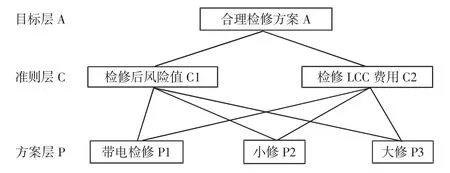
图4 变压器检修决策AHP模型Fig.4 AHP Model of Maintenance Strategy in Transformer

通过建立的递阶层次结构，可以使检修决策问题更加系统化、条理化、层次化。其中，依据2.1章节中的风险评估、3.1章节检修后的故障概率计算及3.2章节LCC分析可以分别计算三种待选检修方式后的风险值及LCC费用。

（2）构造两两比较判断矩阵，以A表示目标，ui、uj（i，j=1，2，…，n）表示因素，uij表示ui对uj的相对重要性数值，用1-9比例标度法确定并由uij组成A-U判断矩阵P。

表1 1-9比例标度准则Tab.1 1-9 Scale Criterion

用比例标度将决策者的判断量化，这一步直接影响决策结果。由于本模型中准则层指标均为变化量，因此需要引入数量性指标的比例标度计算方法[11]，按式（11）确定比例标度，从而构造判断矩阵进行比较。

式中：bij—标度函数；k—全部元素中，P指标的最大值与最小值之比；b—与k相对应的元素相对重要程度标度；p—调整系数。当选取准则为指标值越大越好时，取值1；反之取为-1。

（3）依据判断矩阵计算单一准则下元素的相对权重及一致性检验。

（4）层次总排序。分别得到带电检修、小修和大修三种方案对目标层的合成权重，并进行排序，选取权重最大的检修方案，为主变压器的检修决策提供依据。

5 算例分析

为说明研究成果应用于检修决策的有效性，以多台待检修主变压器为例进行计算分析。多台待检修主变压器的参数，如表2所示。

表2 主变压器参数Tab.2 Parameters of Main Transformer

5.1 风险评估计算

分别计算A、B、C三台主变压器检修前的故障概率、可能损失的资产及风险值并依据风险评估结果给出检修次序。计算结果，如表3所示。从上述计算结果可以看出，检修顺序依次排列为C、B、A。选择主变压器C为例，给出检修决策方案。

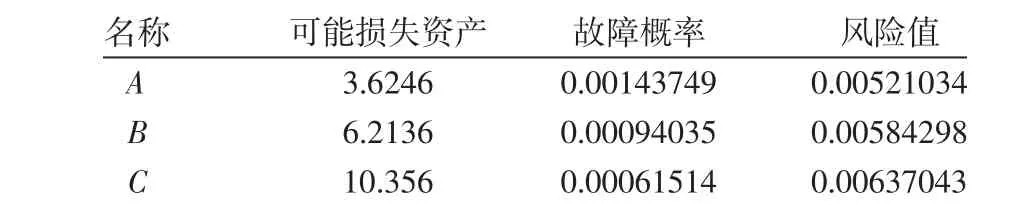
表3 风险评估计算结果Tab.3 Calculation Result of Risk Assessment

5.2 检修后故障概率计算

为计算主变压器C在不同检修方式后的风险值及LCC费用，需计算检修前C的等效役龄及不同检修方式后的故障概率。计算结果，如表4、表5所示。

表4 主变压器C检修前的等效役龄Tab.4 Equivalent Age of Main Transformer C Before Maintenance

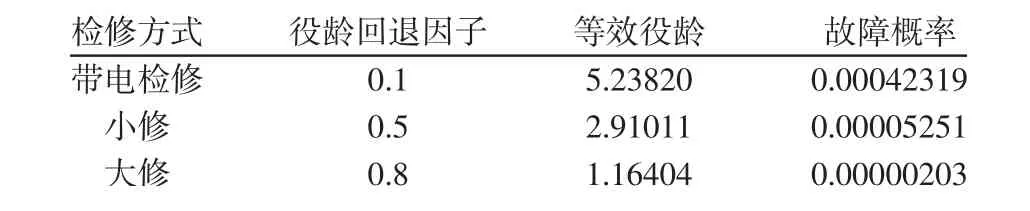
表5 主变压器C不同检修方式后的故障概率Tab.5 Failure Rate After Different Maintenance Methods of Main Transformer C

5.3 不同检修方式后风险值及LCC计算

选取现场故障修复费用6万元；因故障导致的停电损失费用80万元；主变压器单次带电检修费用0.35万元；单次小修费用1.5万元；单次大修费用8万元。并依据上述三种检修方式后的故障概率，计算三种检修方式后的风险值及LCC费用，如表6所示。

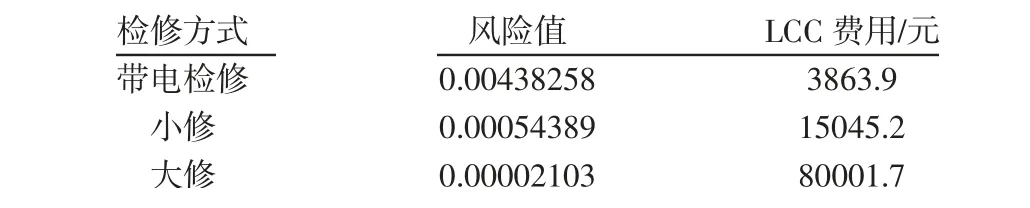
表6 主变压器C不同检修方式后的风险值及LCCTab.6 Risk Value and LCC After Different Mainten ance Methods of Main Transformer C

5.4 检修决策AHP模型计算

根据上述计算结果，在已经构造的AHP模型下计算主变压器C的三种不同检修方式总权重，如表7所示。

表7 P层指标权重计算结果Tab.7 Weight Calculation Result of the P Layer Index

因此，对主变压器C采用大修的方式可以兼顾检修风险和成本，为最优决策方式。同理，按照上述方法计算主变压器A、B的相关结果可以给出最优检修决策。

5.5 应用软件

在主变压器风险值及LCC计算过程中涉及过多复杂、繁琐的步骤以及采取AHP决策计算过程中涉及大量矩阵计算。为了能使计算简便快捷，便于工程实际的应用，使用图形化编辑语言，在LabVIEW软件下编写了主变压器检修程序。由于源代码公开，具有良好可扩展性，更加适合硬件工程师、实验室技术人员、生产线技术人员在工程领域的使用。考虑到将来设备状态参数直接从现场采集，使得软件更具有针对性，因此采用LabVIEW作为开发平台，设计了简洁明了的用户界面，如图5所示。该软件综合考量了技术和经济指标，软件界面简洁、易用，有丰富的在线帮助系统，使得检修方案的制定更加便捷、合理。检修决策算法的软件实现过程如下：首先输入待检修主变压器的参数，电压等级和容量参照导则规定选取，另外状态评分和容量也不能为0，否则软件无法进行风险计算，防止了错误填写的发生。风险计算完成后，风险比较按钮禁用取消，可以将比较结果显示在下面的文本框内。输入其余待检修变压器参数依次计算风险值并进行比较操作。风险比较操作完成后，清空按钮和检修排序按钮的禁用取消，清空操作会将文本框内容初始化，最后点击检修排序会给出优先检修的建议。多台变压器风险计算结果及检修建议，如图6所示。

图5 变压器容量填写不符合要求Fig.5 Capacity of the Transformer Does Not Meet the Requirements

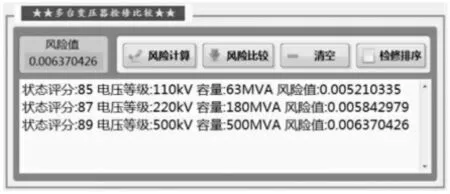
图6 多台变压器风险计算结果及检修建议Fig.6 Risk Calculation Results and Maintenance Suggestions of Multiple Transformers

之后选取风险值最大的第三台变压器进行风险计算并设置LCC的费用，完成后点击检修方式按钮会得到建议采取的检修方式。此外点击查看数据按钮打开详细数据面板，可以查询完整的计算过程并且可以根据软件的Excel模板导出将结果保存到本地，方便后期查看。最后还可以打开软件的帮助文件或查看帮助文件内的作者联系方式，获取更多帮助。检修方式决策、Excel导出示意图，如图7、图8所示。

图7 检修方式决策Fig.7 Strategy of Maintenance Method

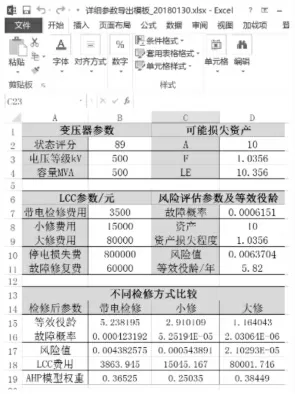
图8 Excel导出Fig.8 Excel Export

5.6 算例小结

从5.1到5.4节的结果和分析可以看出，应用AHP模型下的检修决策算法能够综合考虑主变压器检修的风险及LCC，在有效降低检修风险的前提下提高主变压器检修效率，减小检修维护成本。并且为便于工程实际应用，5.5节开发了基于LabVIEW的主变压器检修软件，实现了主变压器的检修排序及检修的最佳方式判断。

6 结论

为从技术性和经济性双维度实现检修决策方案优化，进一步节约检修维护成本，研究一种将主变压器风险评估和LCC技术相结合的检修方案，得出以下结论：（1）采用缺陷指数计算检修前变压器故障概率可以有效避免指数关系拟合带来的巨大误差；（2）引入役龄回退因子可以将故障概率与变压器运行时间相关联，以实现不同检修方式后的故障概率推算；（3）建立检修决策方案的AHP模型将风险值和成本结合，以权衡检修时的可靠性及经济性要求；（4）算例详细分析了主变压检修决策方案过程，得到经济合理的检修方案，验证了此方法的可行性并编写应用软件实现了检修决策算法，可为提高主变压器检修的技术性和经济性提供重要的算法支撑。