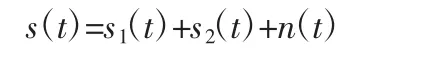EEMD结合小波包的振动筛轴承信号降噪效果分析
朱 敏,段志善,郭宝良
(西安建筑科技大学机电工程学院,陕西 西安 710055)
1 引言
滚动轴承是机械设备应用最广泛的部件之一,也是最易损坏的元件之一[1]。所以对滚动轴承进行检测是非常必要的,提取滚动轴承的故障特征频率是诊断滚动轴承故障的关键[2]。轴承发生故障,故障信号大多数表现为非平稳的冲击脉冲信号,其宽度较窄[3],在实际测量当中,设备的工频以及背景噪声往往会淹没冲击信号。
集合经验模态分解方法将噪声辅助分析应用于经验模态分解中以促进抗混分解,有效抑制了模态混叠现象[4-5]。经EEMD分解得到的固有模态函数能揭示原信号的物理内涵,使每个IMF的物理本质更为清晰。
传统的消除噪声的方法是基于傅里叶变换的带通滤波器实现,但是这种滤波容易将信号中的部分非噪声信号也一起滤掉,因此效果并不理想。这些年小波降噪取得了较大的进展,尤其在机械故障诊断以及降噪处理方面具有良好的效果。
在经验模态分解中,对于IMF分量选取的问题一直入了排列熵的概念,当某一分量排列熵值大于0.6时,就舍去这一分量,这种方法很容易删去有效的信号。文献[8]计算各IMF分量相关函数与原信号自相关函数的相关系数,根据相关系数来选择合适的IMF分量,但是未给出相关系数的取值范围。
提出了基于EEMD与小波包以及最优降噪准则相结合的信号处理方法。首先利用小波包降噪对仿真信号进行降噪处理,去除信号中噪声的干扰,然后使用EEMD方法对信号进行分解,分解得到的分量构建带通滤波器,通过最优降噪准则选择合适的滤波组合。起到了有效选取IMF分量的目的;并将该方法应用到了振动筛实测信号分析当中,证明了该方法的有效性与实用性,对于同类振动筛的故障诊断具有实际的意义。
2 EEMD方法
EEMD可以有效的解决EMD出现的模态混叠现象。
EEMD算法的实现如下:
(1)对于聚合次数N,白噪声的幅值系数k做初始化设置,设m=1。
(2)在第m次信号中加入白噪声信号

(3)将加入白噪声的信号分解为一系列的模态分量(IMF)。
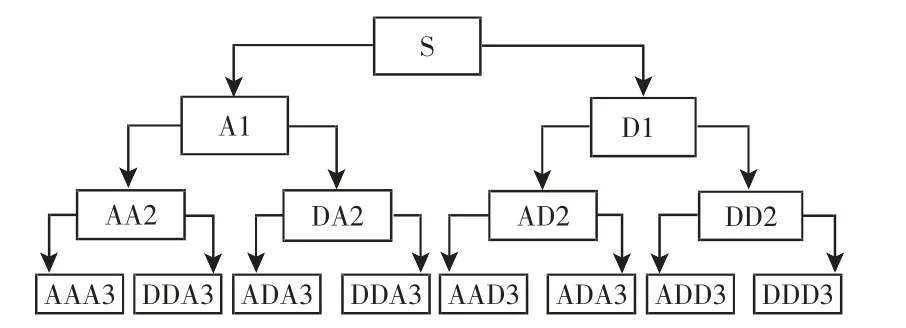
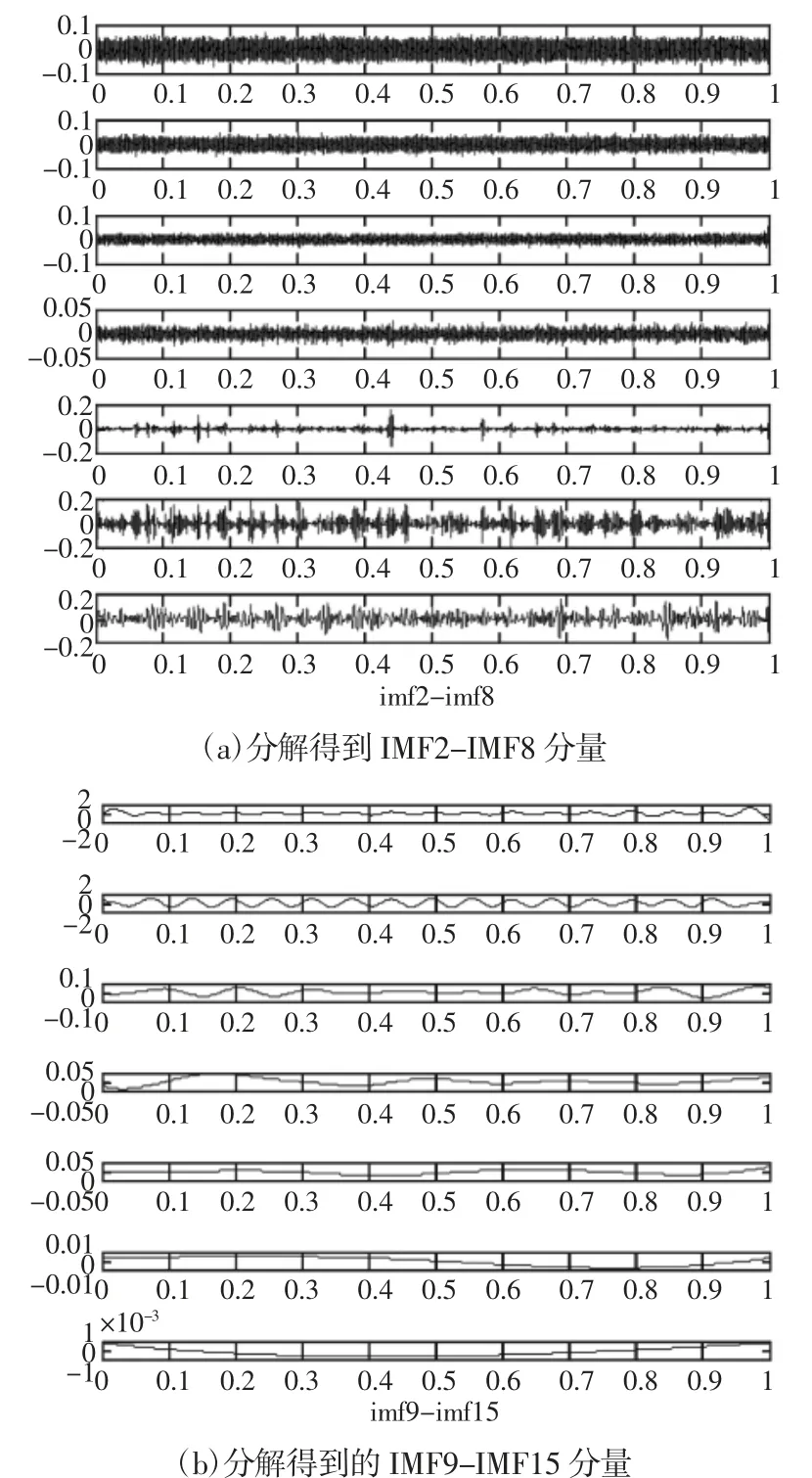
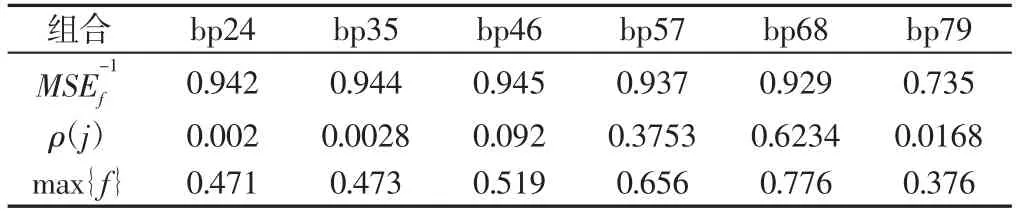
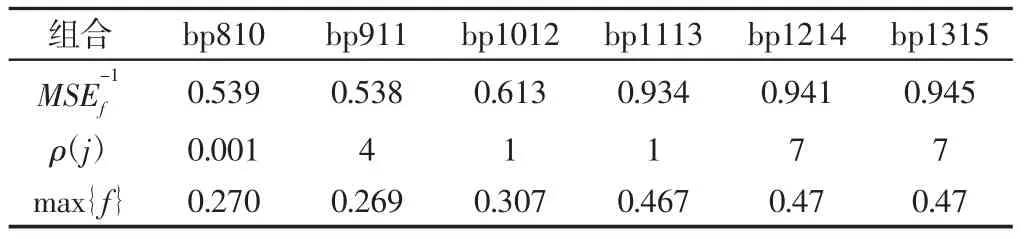
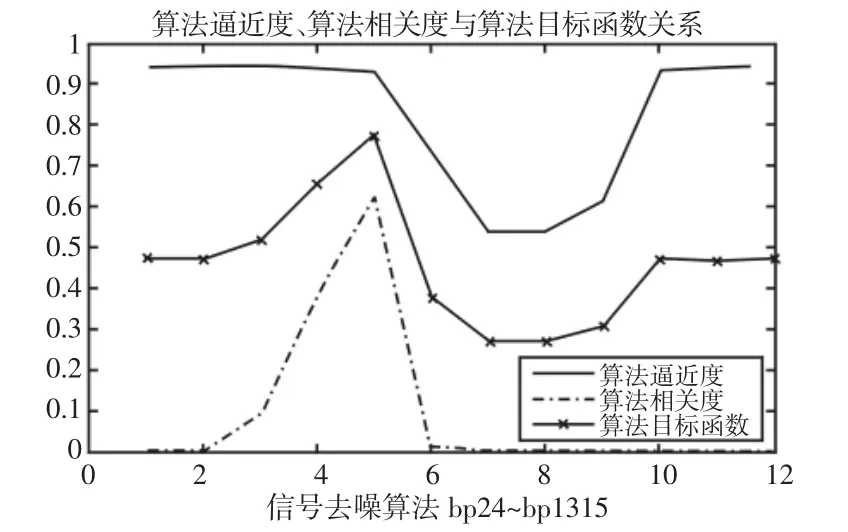
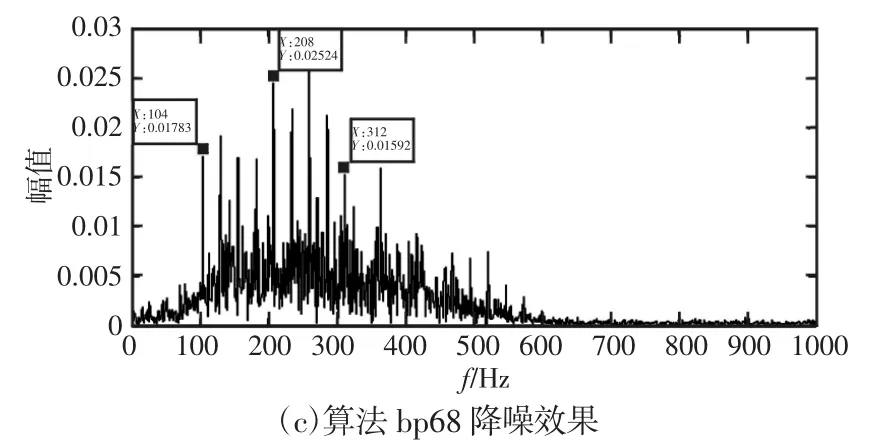
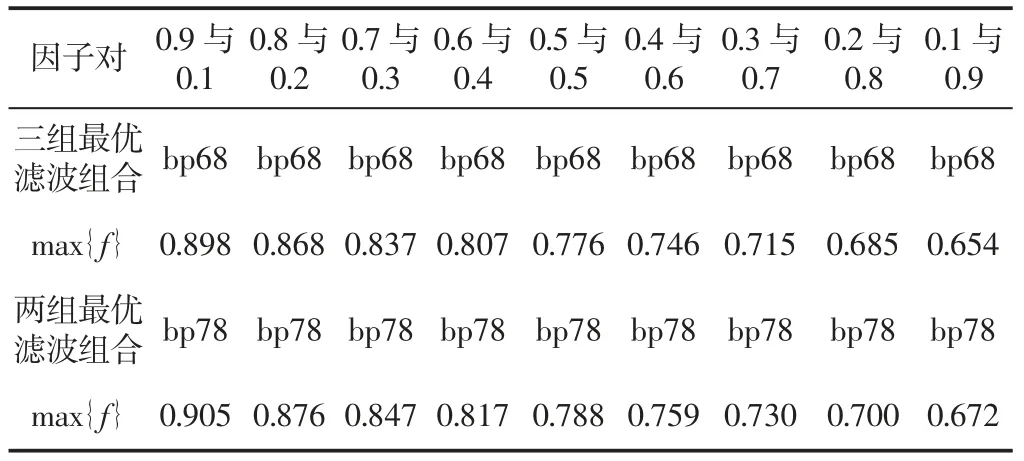
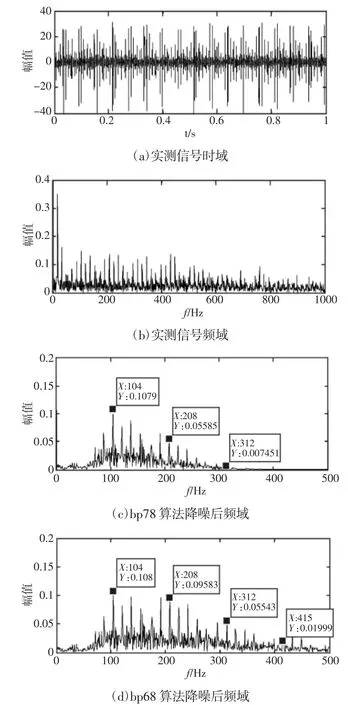
(4)当m (5)将N次得到的IMF分量做平均 式中:ci,m—第m次分解得到的第i个IMF; N—经验模态分解的聚合次数。 (6)把每个IMF的N次分解平均值作为最终的模态函数。 小波包变换是基于小波变换的进一步发展。 下面是小波包降噪的具体步骤: (1)将信号进行N层小波包分解,三层小波包分解,如图1所示。 图1 小波包3层分解树Fig.1 Wavelet Packet 3 Layer Decomposition (2)利用最小代价原理,计算最佳小波包基。 (3)小波包分解系数的阈值量化,对每一个小波包分解系数,选择一个适当的阈值对左右的小波包基进行阈值量化。 (4)将小波包重构,重构的信号即为最优小波包降噪处理后的信号。 为说明方便,我们将采集得到的滚动轴承信号简化为向量形式: 式中:xi—再第i时刻采集得到的含噪轴承振动加速度信号数值。 定义降噪偏差均方差为: f。 由定义可知,降噪偏差均方差MSEf累加了含噪原始信号与降噪后信号的全部偏差,反应了降噪结果接近原始信号的程度。 求各IMF分量自相关函数与原信号自相关函数的相关性,即相关系数。为了避免将幅值较小而又真实的IMF分量被去除,需要对自相关函数做归一化处理。 相关系数的计算: 先计算出原信号与各个IMF分量的自相关函数,并做归一化处理Rx,RIMF1,…,RIMFk,的计算公式为: 求RIMF1,…,RIMFk与Rx相关系数。相关系数的计算公式为: 式中:N—信号的点数;j—第个IMF分量。 ρ(j)值越大,对应的IMF分量与原信号相关性越好。 上述介绍了EEMD与小波降噪算法,用此算法将含噪信号x(t)分解得到IMFk(t)(k=1,2,…,K)为固有模态分量,R(t)为余项。 这时,可以设计低通滤波器为: 高通滤波器则可表示为: 同样的,带通滤波器可表示为: 不同的,对于振动筛轴承来说,噪声信号为周围环境产生的高频振动干扰信号,还有低频的振动筛工频信号,为了将这两种信号滤除,所以选择带通滤波器最为合适。 我们既要关注降噪结果逼近原始信号的情况(即算法逼近度MSE-f1越大越好),同时也要关注滤波后的信号与原始信号应该充分相似的要求(即算法相关度ρ(j)越大越好)。因此优良降噪算法判定准则是: 约束条件: 降噪算法的目标函数为: 式中:α,1-α—算法逼近度影响因子和相关度影响因子,其选择权重依据信号处理的具体要求而定。 轴承最常见的故障是内外圈点蚀故障,所以选择滚动轴承外圈点蚀故障进行数据仿真。仿真所用到的轴承尺寸为1308调心轴承。轴承参数,如表1所示。计算所得轴承外环故障频率为104.18Hz,振动筛工频为16.7Hz。 表1 轴承参数Tab.1 Bearing Parameters 轴承的数据包括电动机产生的工频信号,外圈点蚀产生的周期性冲击信号,还有系统产生的噪声干扰。仿真信号使用周期为16.7HZ的正弦信号s1来代替振动筛工频信号;gauspuls脉冲分量s2来代替轴承外圈点蚀产生的冲击信号;标准差为0.1的白噪声代替原始信号中的噪声干扰。信号在测量当中还会产生系统误差,这里不予考虑。以上三种信号构成了原始信号s。 图2 含噪振动筛轴承仿真信号Fig.2 Simulation Signal of Noise Bearing Vibrating Screen 首先对原始信号进行小波包降噪处理,处理的时域图,如图2、图3所示。可以看出小波包降噪去除了大部分的白噪声干扰。接下来对轴承信号进行EEMD分解得到了15个IMF分量,以及一个余项,分解得到的分量,如图4所示。 图3 经小波包降噪后的信号Fig.3 The Signal After Wavelet Packet De-Noising 图4 经EEMD分解得到的模态分量Fig.4 Modal Components Obtained by EEMD Decomposition 去掉第一个噪声分量IMF1以及余项r(t),考虑IMF2IMF15组成带通滤波器,因为相邻的IMF分量频率最为接近,有可能为倍频成份,所以带通组合最少的个数为两个IMF分量,又因为相隔较远的IMF分量差别较大,所以我们取带通组合最多个数为3个IMF分量。我们以带通滤波IMF5+IMF6+IMF7为例,简记为bp57,即带通滤波由IMF5到IMF7的分量构成。先来分析三个分量组成的滤波器,我们可以得到以下滤波组合形式:由三个IMF分量组合而成,共有12组组合分别是bp24、bp35、bp46、bp57、bp68、bp79、bp810、bp911、bp1012、bp1113、bp1214、bp1315。由两个IMF分量组合而成,共有13组组合。考虑到信号处理工作主要是进行振动筛轴承冲击信号的识别以及轴承故障的分析,因此,影响因子α,1-α分别选定为0.5,0.5,也就是算法逼近度与相关度的影响相当。经过多次重复计算,得到的12组滤波组合算法逼近度与相关度及目标函数值见下表1、2,算法逼近度与相关度及目标函数的走势图,如图5所示。 表2 算法逼近度、相关度、目标函数数据(bp24-bp79)Tab.2 Algorithm Approximation,Correlation,Objective Function Data(bp24-bp79) 表3 算法逼近度、相关度、目标函数数据(bp810-bp1315)Tab.3 Algorithm Approximation,Correlation,Objective Function Data(bp810-bp1315) 图5 各个算法逼近度、相关度、目标函数走势图Fig.5 The Degree of Approximation,Correlation and Objective Function of Each Algorithm 由表中可以看到bp46、bp57、bp68的目标函数值比较大,其中bp68值为最大0.776。 分别对三个带通滤波组合做频谱分析,由下图可以看出bp46、bp57缺少了一倍频的成分,而bp68能够很好的保留了104HZ的倍频及边频成分,其他频率成分被大部分滤除。所以bp68的带通滤波器对于处理此类振动筛得到的结果是最优的 图6 算法bp46、bp57、bp68降噪效果Fig.6 Algorithm Bp46,bp57,Bp68 Noise Reduction Effect 实际上,对于影响因子对0.9和0.1,算法bp68目标函数值最大,其值为0.898;而对于影响因子对0.8和0.2,算法bp68目标函数值也为最大,其值为0.868;以此类推,影响因子取任意值,最终都是算法bp68目标函数值最大。影响因子对,目标函数值以及对应的算法,如表3所示。 利用表1、表2与表3综合分析我们可以得到:在此振动筛仿真信号处理中,算法bp68为最优,目标函数值为最大。 表4 影响因子对、目标函数值及优良算法Tab.4 Influence Factor Pair,Objective Function Value and Excellent Algorithm 接下来分析由两组IMF分量构成滤波器组成的情况,如表4所示。不同因子对,最优的滤波器及目标函数值都已经列出。从表可以看出,两组分量组合而成最优的滤波组合为bp78,对比bp68可以发现,三组与两组IMF滤波组合形式数值差异并不明显,所以需要进一步用实验信号来验证bp68与bp78哪一个效果更好。 以上分析了优良降噪算法在轴承仿真信号的效果。我们进行数据采集实验,实验用到的振动筛及传感器测点,如图7所示。 图7 实验所用到的振动筛及其测点布置Fig.7 The Shaker Used in the Experiment and Measuring Points 我们完全利用上述选定的两组降噪算法bp68与bp78及实现程序,得到实测振动筛外圈点蚀故障轴承的降噪效果图,如图8所示。原始信号的时域图,如图8(a)所示。原始信号的频域图,如图8(b)所示。使用bp78算法降噪后的频谱图,如图8(c)所示。由图中可以看到外圈故障频率被完整的保留了下来,其他频率成分均被滤除,但是三倍频不明显。使用bp68算法降噪后的频谱图,如图8(d)所示。由图可以看到,一倍频104Hz、二倍频208Hz以及三倍频312Hz幅值比较高,故障信号被完整保留下来,降噪效果更加明显。由此分析得到bp68在实测轴承信号降噪中效果最好。 图8 实测振动筛轴承信号时频分析Fig.8 Time Frequency Analysis of Measured Bearing Signals of Vibrating Screen 利用振动筛轴承信号模型: 来分析降噪算法的有效性和实用性,并将得到的结论应用到了轴承实测信号当中。 (1)提出了EEMD结合小波包以及最优降噪准则的算法,可以有效减少噪声干扰。 (2)采用EEMD方法得到不同的IMF,构建不同的带通滤波器组合,根据设计的判别准则选定优良算法。即通过平衡算法相关度和分量相关函数的相关系数,来选择所需要的IMF分量。 (3)对于同类振动筛,可以直接用得到的算法与结论处理振动筛轴承信号,处理结果合理有效。
3 小波包降噪算法
4 降噪模型的判定准则
4.1 降噪偏差均方差与算法逼近度


4.2 自相关函数与相关函数的相关系数

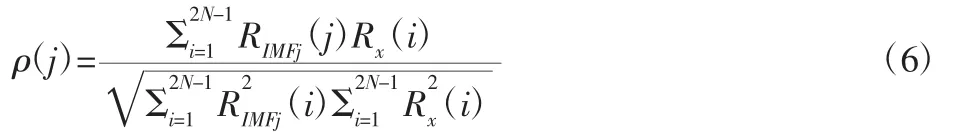
4.3 降噪算法的判定准则





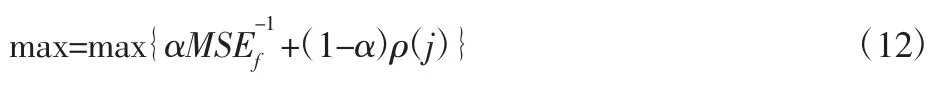
5 振动筛故障轴承仿真信号分析





6 振动筛实测信号的降噪效果

7 结论