基于一般集对评价法的节水灌溉方案优选

张 虎 陈 杰

（1.安徽省·水利部淮河水利委员会水利科学研究院 水利水资源安徽省重点实验室 蚌埠233000 2.安徽省地球物理地球化学勘查技术院 合肥 230022）

节水灌溉方案优选就是从多种给定的工程方案中，经过系统地分析与评价，从而做出决策，选择最佳方案。方案优选主要考虑项目的技术、经济、生态和社会等几个方面，如灌溉水利用率、投资回收期、作物适应性、项目受欢迎程度等相关指标，然而这些评价指标既有正向的影响，也有负向的影响，还有不确定性的影响。评价指标的模糊性、不确定性以及人为因素的主观性，给方案优选工作带来了一定的难度[1～2]。为此，本文利用一般集对评价法（general set pair analysis assessment method，GSPAAM）对节水灌溉方案优选方法进行了实例研究与应用。

1 一般集对评价法模型

1.1 模型原理

首先，根据具体问题，将集合A 和集合B 组成集对H=(A，B)。然后，对集对H 的特性展开分析[3～5]。

假设集对H 的特性总数为n，其中S 为同一性的个数，P 为对立性的个数，F= n-S-P 为两个集合既不对立又不同一的个数（F 为差异性个数），所以，得出两个集合的联系数表达式为：

式中：a、b、c 为集对的联系度分量，并且满足a+b+c=1 的归一化条件。

式（2）从不同角度定量解释了确定性与不确定性。a、c 是相对确定的，b 是相对不确定的。

1.2 模型计算步骤

模型计算步骤如下[5]：

步骤1：将各等级标准进行符号量化处理。对于1 级标准，记为集合B1=（1，1，…，1）；对于2级标准，记为集合B2=（2，2，…，2）；依此类推，对于K 级标准，记为集合BK=（K，K，…，K）。

步骤2：将评价对象A 进行符号量化处理。评价对象A 的各指标值与对应指标各级的标准值进行比较，如落入第1 级，该指标为第1 级，将该指标量化为符号“1”；如落入第k 级，将该指标量化为符号“k”。逐个指标依次比较，得到符号量化的集合A，比如A1=（1，3，…，3）。

步骤3：构造集对H=（A，Bk）。将A 与Bk相对应的元素一一进行对照，统计符号相同的个数，记为S；统计符号相差1 级的个数，比如2 与1、2与3，记为F1；统计符号相差2 级的个数，比如2 与4、1 与3，记为F2；依此类推，统计相差K-2 级的个数，比如2 与K，记为FK-2；统计相差K-1 级的个数，比如1 与K，记为P。得到K 元联系度：

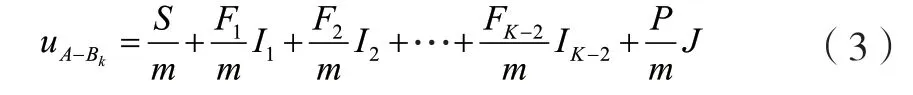
式中：S+F1+F2+…+FK-2+P＝m。

步骤4：确定差异不确定分量系数I1，I2，…，IK-2的值。差异不确定分量系数可以采用经验取值法或均匀取值法来确定。

步骤5：将I1，I2，…，IK-2和J 代入上式中得到综合评价指标值——联系数，即kBAu−′（k=1，2，…，K）。根据联系数的大小判断A 所属的评价等级，联系数最大者对应的等级就是A 的评价，即根据kBAu−′推断A 为第k 级。 如 3BAu−′最大，则推断A 为第3 级。

2 案例应用

本文基于一般集对评价法模型，对某节水灌溉项目的管道灌溉、喷灌、滴灌和小管出流灌溉等4个待选方案的11 个技术经济评价指标进行综合评价与分析，选出最佳方案，作为项目决策的重要依据[6～9]。各待选方案评价指标见表1。

建立各方案的评价指标体系：净现值x1（万元），收益率x2（%），投资回收期x3（a），效益费用比x4，灌水均匀度x5（%），灌水强度x6（mm·h-1），灌水利用率x7（%），安全可靠性x8（%），作物适应性x9（%），农民欢迎程度x10（%），便于施工程度x11（%）。各方案的均值与均方差见表2。

根据本案例，应先确定各等级标准。根据均值标准差法将各指标分为三个级别：好（1 级）、中（2级）、差（3 级）。具体划分为：对于越大越优的指标，1 级、2 级、3 级分别对应区间[x+k2s，+∞)、[x+k1s，x+k2s)、(0，x+k1s)，其中，x、s 分别为各方案技术经济评价指标值的均值和均方差，经验系数k1=-0.5，k2=0.5；对于越小越优的指标，1 级、2 级、3 级分别对应区间(0，x+k1s)、[x+k1s，x+k2s)、[x+k2s，+∞)，k1、k2同上。评价等级标准见表3。

把各方案确定为集合Ai(i=1，2，3，4)。方案1（A1），方案2（A2），方案3（A3），方案4（A4）。然后根据表3，将集合Ai(i=1，2，3，4)进行符号量化处理，计算结果见表4。最优等级标准为集合B1(1，1，1，1)，将集合Ai(i=1，2，3，4)与B1(1，1，1，1)构建为集对H=(Ai，B1)(i=1，2，3，4)。统计集对H 符号相同的个数，符号相差一级的个数和符号相差二级的个数，最后计算各集对的联系数。

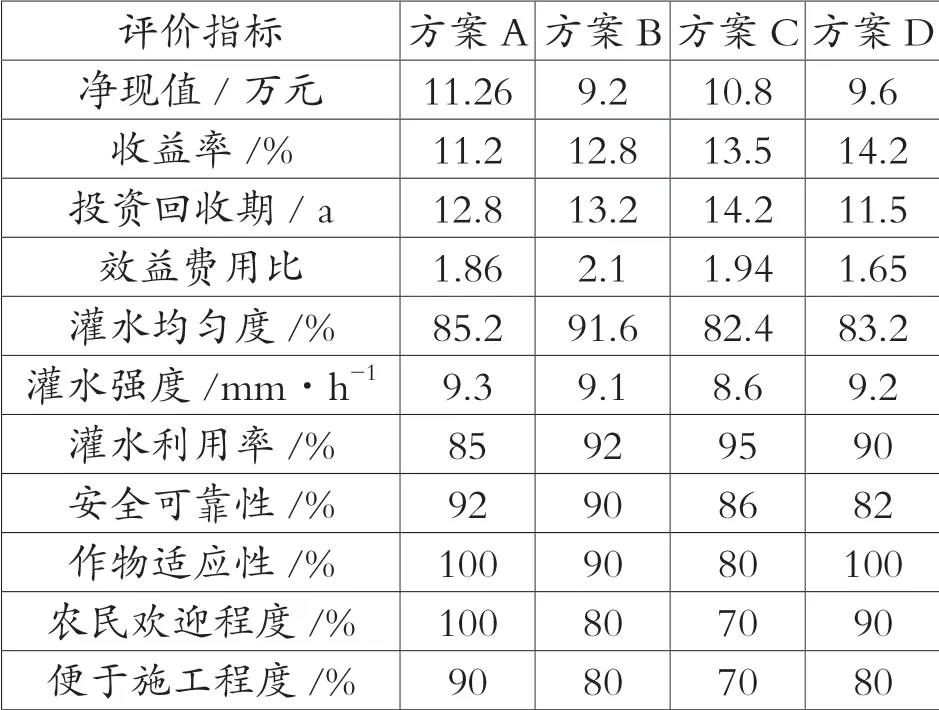
表1 各方案的主要技术经济指标表

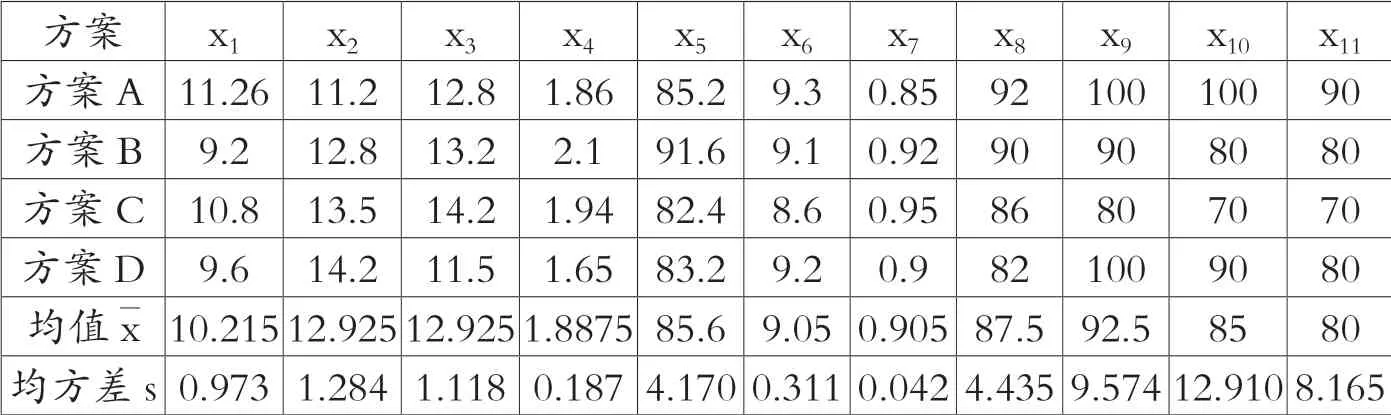
表2 节水灌溉方案指标值及相关统计值表

表3 评价等级标准表

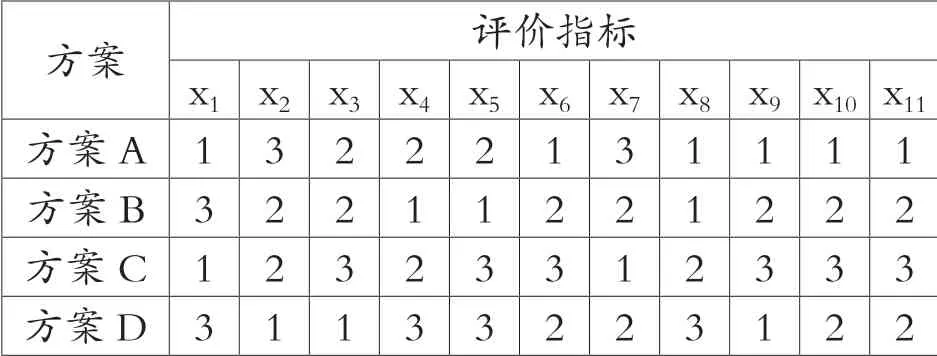
表4 各方案符号量化表

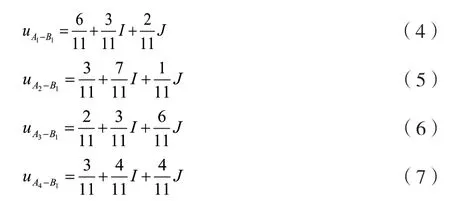
均匀取值法取I=0，J= -1，则各集对的联系数分别为：

得出，方案A最优，其次是方案B，再次是方案D，最差的是方案C。

经验取值法取I=0.5，J= -1，则各集对的联系数分别为：

得出，方案A 和方案B 最优，其次是方案D，最差的是方案C。

从各方案评价指标体系来看，方案A 的11 项指标中有6 项指标为好，3 项指标为中，2 项指标为差，而方案B 的11 项指标中3 项指标为好，7 项指标为中，1 项指标为差。相比较而言，方案A 半数以上指标都为好，故推断方案A 优于方案B。

所以，该案例所有方案优选排序为：方案A ＞方案B ＞方案D ＞方案C。

3 结语

（1）节水灌溉方案优选涉及到多个指标和因素，是一个比较复杂的系统评价问题。本文通过建立一般集对评价模型，在处理各种不确定问题上，把众多评价指标变换成单一综合评价指标，从而简化了思路，易于计算与操作，为含有多个指标的节水灌溉方案优选问题提供了一种较为可靠的决策依据。

（2）评价结果说明了差异不确定系数分量取值过程有人为主观因素的干扰，直接影响了最终的评价结果。因此，在方案优选决策中尽量降低人为因素的影响，减小决策者的偏好，对方案最后的优先结果有着重要意义。

（3）一般集对评价法理论的不足之处是没有充分考虑评价指标的等级边界的模糊性以及各评价指标的权重，在今后的研究中，考虑这方面的内容会使评价结果更加稳定与合理。