基于水均衡原理的北方隐伏岩溶含水层参数求取方法
扈剑琨 姬永红
(山东省济宁市兖州区行政审批服务局 济宁 272100 山东省鲁南地质工程勘察院 济宁 272100)
1 引言
在地下水资源计算与评价工作中,水文地质参数是必不可少的基础数据[1][2],储水系数是含水层的基本参数之一。由于含水层的井流理论已经非常成熟,所以目前求取含水层各种参数最流行的方法就是开展抽水试验[3][4],然后根据实际水文地质条件,选择相对应的解析公式进行计算以获取各种参数。水文地质参数的计算公式非常多,而且理论依据充分,为水文地质工作者提供了很好的技术支撑。
尽管抽水试验法计算公式丰富,理论依据充分,是当前求取水文地质参数的主要方法,但根据生产实践来看,该方法存在以下局限与不足:①自然界实际水文地质条件千差万别,很难找到与之完全匹配的理论公式;②含水层的非均质特性,使求得的参数只能反映抽水井所在小范围区的数值,不能用于较大范围的区域地下水资源计算;③稳定流理论本身的局限性[5],致使计算结果与实际有偏差;④非稳定流抽水试验用时长,投资大,不适合在一般性评价工作中应用。
岩溶含水层明显有别于孔隙介质含水层,其高度各向异性与非均质性使得含水层中出现紊流的可能性增大[6],而北方岩溶水系统高度开放、补源众多,以及各种水体互相转化复杂的特点[7],为通过抽水试验利用解析公式求取水文地质参数带来了更多的困难。
本文基于水均衡原理建立地下水系统水均衡方程,再利用实际监测数据解方程是求取含水层水文地质参数,是一种间接求参方法。该方法理论简单,操作方便,在地下水资源评价的初级阶段或区域性地下水资源计算工作中一般可取得较为理想的效果。
2 水均衡原理求取含水层参数的方法原理
根据水量均衡原理,对于某一特定地下含水系统,在某一均衡期内的补给量与排泄量之差应等于含水层中水的贮存量的变化量:

式中:Q补—地下水补给量(L3/T);Q排—地下水排泄量(L3/T);S—含水层给水度(潜水含水层)或储水系数(承压含水层);F—计算面积(L2);Δh—含水层在均衡期内平均水位变幅(L);Δt—均衡时段天数(T)。
当Q补大于Q排时,地下水系统处于正均衡,地下水位上升,Δh 取正值;当Q补小于Q排时,地下水系统处于负均衡,地下水位下降,Δh 取负值。
分析(1)式,对于特定含水系统,计算区面积F 是已知的,均衡期时间可以根据需要人为选定,水位变幅Δh 由实测数据统计而来。如果能够获知Q补与Q排,则解方程(1)即可求得含水层的给水度或储水系数S。
现实中,每个地区不同时段地下水的补排项都不尽相同,实践中可以根据实际水文地质条件,对Q补与Q排进一步分解,再灵活运用(1)式,则可以求得含水层各种不同参数。
3 计算实例
3.1 研究区概况
鲁西地区某隐伏型岩溶水系统总面积约516.6km2,南部地段有小面积的碳酸盐岩出露,其余大部分为隐伏状态。第四系覆盖层由南向北逐渐增厚,底部普遍分布一层厚度15~20m 的粘土层,形成了第四系孔隙含水岩组与岩溶含水岩组之间的弱透水层。除南部出露区可接受少量降水入渗补给外,上覆孔隙水的越流补给是岩溶水系统的主要补给来源。岩溶水总体向北径流,中北部地段人工开采是其唯一排泄途径。研究区水文地质条件可概化为图1 所示,即整个系统可划分为两个含层:上覆孔隙含水层按潜水处理,下伏岩溶含水层具承压性,两个含水层之间通过弱透水层以越流方式发生水力联系。岩溶含水层在上游裸露山区可接受大气降水入渗补给,在中、下游地段接受孔隙含水层的垂向越流补给,岩溶水通过人工开采排泄,但因与煤系地层接触而不存在侧向排泄。
3.2 参数计算
根据(1)式,结合实际水文地质条件,可建立研究区岩溶水系统的水量均衡方程:

式中:Q雨—降雨入渗补给量(L3/T);Q越—越流补给量(L3/T);Q开—人工开采排泄量(L3/T)。
(2)式中除含水层储水系数S 外,还需要计算降水入渗系数与越流系数。为简化计算,可以选择枯水季节无降水补给的时段进行计算,则(2)式可改写为:

式中:K M′′—弱透水层的越流系数(T-1);ΔH—孔隙含水层与岩溶含水层平均水位差(L)。
(3)式中岩溶水水位变幅Δh、孔隙水与岩溶水平均水位差ΔH 及开采量Q开均可由动态监测资料而得,计算面积F 及计算时段Δt 为已知量,方程中有岩溶含水层的储水系数S 和弱透水层的越流系数K M′′两个参数需要计算。
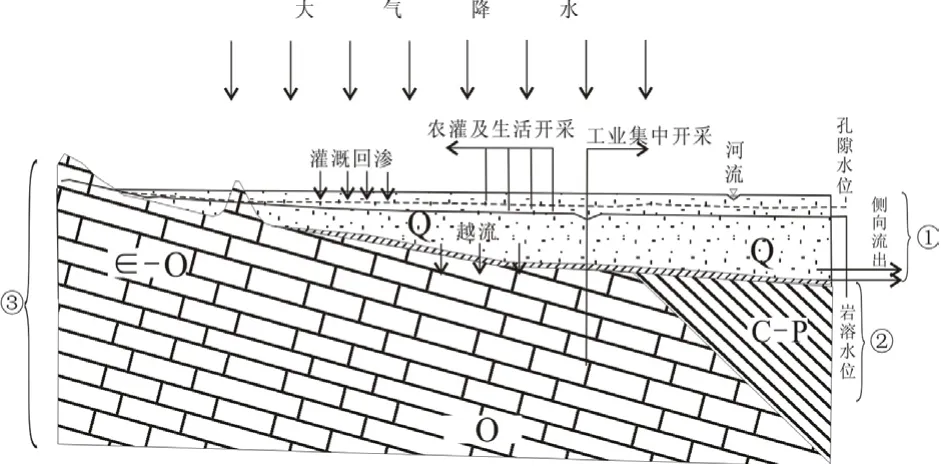
图1 研究区地下水系统概念模型图
本文分别选取2004年1~4月(121d)、5月10日~6月18日(40d)两个时段作为均衡期,该两个时段基本无降水补给,岩溶地下水开采量由孔隙含水层越流补给与岩溶含水层自身弹性释放共同维持,则根据(3)式可分别列出对应于以上两个时段的均衡方程,从全区范围内统计出两个计算时段含水层各变化量(见表1),可得方程组:
将表1 各参量代入(3)式并解方程组,即可得S=2.78×10-3、KM′′=2.96×10-5(1/d)。
此结果即为计算区岩溶含水层综合储水系数与弱透水层综合越流系数值。
实践中,每个研究区的补排条件都不同,根据实际条件,选择适合的均衡期,对(1)式做合理变换,即可求得各种不同的参数。
3.3 计算结果验证
为验证参数的可靠性,选取已知资料的其他时段对参数进行验证,其方法实际上是上述求参过程的逆运算,即用求得的参数及某时段内开采量(或水位降深)等已知条件推算岩溶水位降深(或开采量),再与实测资料对比,如二者一致或接近,则表明所求参数正确可靠。
以2004年7月1日~9月30日(92d)为例,该时期内研究区岩溶水系统同时接受孔隙水越流补给和裸露区大气降水入渗补给,主要经水源地集中开采排泄。
经实测,该时段(t=92d)内孔隙水与岩溶水平均水位差ΔH 为1.58m;降水入渗补给量为5.89 万m3/d;开采量为5.0 万m3/d。将各已知量代入(3)式解得该时段岩溶水水位变幅Δh 为2.83m,实测2004年7~9月岩溶地下水位平均上升2.89m,计算结果与实测值较接近,说明所求参数值比较可靠。
4 结语
该方法的优点在于:(1)不需开展抽水试验,省时、省力、省资金;(2)求取的是整个研究区的综合性参数,回避了非均质含水层中抽水试验求参的局限性;(3)方法简单灵活,只需要一定数量的地下水动态监测资料,做合理变换,简单计算即可达到目的。该方法适用于地下水资源评价的初级阶段或区域性地下水资源计算工作。实际运用过程中如果遇到研究区较大、各地水位变幅Δh(或ΔH)差异较大的情况,可以适当将计算区剖分为多个分区分别计算以减小误差,但应注意剖分后各分区之间的侧向水量交换问题■

表1 各均衡期已知常量统计表

