把握引导的“火候”，让数学学习走向深入

■福建省厦门市同安区第三实验小学 张雅妙

《义务教育数学课程标准(2011 年版)》指出：“有效的数学教学活动是教师教与学生学的统一，学生是数学学习的主体，教师应成为学生学习活动的组织者、引导者、合作者。”由此可见，教师作为引导者的角色不容小觑。那么，教师在课堂上如何把握引导的“火候”，让数学学习走向深入？多年的教学经验告诉我，小学数学教学若能及时做好“四谋”，方能帮助学生累积学习的经验，也能助推教学进度，提升教学效益。

一、谋时机，建立深刻的表象

孙子兵法云：“谋定而后动，知止而有得。”在教学中，教师要根据课堂的生成，找准时机，“该出手时就出手”，对学生的回答进行适时、有效的引导，为课堂起一个推波助澜的作用。例如，在教学《毫米的认识》时，教师在让学生感知“1 毫米”的长度中出现了这样的对话。教师：同学们，请你们像老师这样，先把一枚2 分的硬币用食指和大拇指捏住，然后用另一只手轻轻地将硬币抽回，食指和大拇指保持不动。再看看这道缝隙，你觉得1 毫米的长度带给你的感觉是怎样的？学生1：太小了。学生2：太窄了。学生3：太细了。学生4：我在看的时候，眼睛都忍不住眯起来了，手也颤抖了。教师：哇，你的描述很生动。能说说你的手为什么会颤抖吗？学生4：因为1毫米的长度实在太小太小了，我的食指和大拇指稍不留意就要碰在一起了，眼睛也是要眯着才能看清。

不难看出，如果只是停留在学生的感觉表述上，教师没有在关键时机再加以追问，那么，这样的处理便是流于形式，浮于表面的作秀。一句“能说说你的手为什么会颤抖吗？”的“应景式”的引导，恰是点燃了一把火，让“1毫米”的表象深深烙印在学生的脑海中。

二、谋比较，提升解题的策略

教育家乌申斯基说过：“比较方法乃是各种认识和各种思维的基础。”说明了比较在认知中的作用。比较，就是引导学生从多角度、多方向进行思考。例如，在学习列方程解决实际问题时，学生刚开始会比较排斥这种新方式。那么，如何让学生合理选择解决问题的方法？这时候，就要运用比较的方法。教师出示以下两个题目：“①广场上插着五颜六色的旗子。红旗子有40 面，黄旗子的数量比红旗子的3 倍少50面，黄旗子有多少面?②广场上插着五颜六色的旗子。黄旗子有70 面，黄旗子的数量比红旗子的3 倍少50面，红旗子有多少面?”让学生进行比较，发现第②个问题是逆向思维，用算术解容易出错；而如果采用方程的解法就能化逆向为正向，大大提高了正确率。

简单的一个对比，学生直观地看到用方程解决的优越性。这样的比较不但打破了学生受思维定势的消极影响，还可以培养学生思维的灵活性和创造性，使学生快速找到解题的最佳策略，提高思维的敏捷性。

三、谋整合，沟通知识的联系

（一）公式整合，让多个变成统一

各种计算公式的得出，无非要帮助我们更好地解决数学问题。但，众多的计算公式，有时候会让学生开始“乱”了，于是，错用公式的现象层出不穷。在教学中，将面积计算公式整合，化“多”为“一”，学生体验到了前所未有的成就感。

例如，在《多边形的面积》这一单元的整理与复习中，教师在让学生回顾目前已学的平面图形的面积计算公式后，可以针对学生的困惑处抛出一个问题：“面对这5 个面积计算公式，你认为哪个图形的面积计算公式是万能的？”“长方形，因为它是最早拿出来研究的。”“平行四边形，因为长方形和正方形都是特殊的平行四边形，而三角形和梯形也是通过转化成平行四边形来推倒面积计算公式的？”就在学生畅所欲言的时候，教师要介入其中，“据有关资料记载，‘梯形的面积计算公式是万能的。’对于这一观点，你想怎样来验证呢？”于是，四人小组的学习模式便开始了。学生纷纷动脑、动手，在汇报的时候精彩不断，有举例验证的，有画图解释的，还有借助简单教具演示的。紧接着，教师再通过课件的动态演示，让学生直观地看到其他四个图形的面积计算公式是怎样通过梯形的面积计算公式来演变的。“耳听为虚，眼见为实。”学生愉快地接受了这一结论，“太神奇了！竟然最后学的梯形面积计算公式才是‘老大’啊！”在整理中，将平面图形的面积计算公式进行整合，对于五年级的孩子来说是一个新的尝试，也在他们心中埋下创新的种子。让多个变成统一，学生在争议与验证中思维得以提升，有效实现了数学知识间的沟通与内化。

（二）概念整合，由肤浅走向深入

“植树问题”是一种典型的数学问题，但，很多教师在演绎这个概念的时候都会最后将其归纳概括为“棵数”与“段数”的关系，这固然没错。但殊不知，植树问题在学生的生活经验中随处可见，若将这一个小概念融入一个大概念，也就是“除法”中，探究“点”与“段”的关系，这样反而会有一种“柳暗花明又一村”的感觉。除法，学生在二年级已经学习了，它所求的商其实表示的是“段”，而植树是种在“点”上，自然会对应“点数=商，点数=商+1，点数=商-1”这样的三种情况。如此一来，一个全新的概念摇身一变就成了一个旧概念，新旧整合，学生的认知也由肤浅走向深入，由模糊走向清晰。

四、谋拓展，感悟数学的价值

（一）习题拓展，让学生懂得学以致用

习题是数学课堂的延续，是检验教学成效的一方舞台。用好习题，在习题的讲解中进行拓展，能大大提升习题的价值。例如，在学习《积的变化规律》后，可以出示如下课堂练习（如图1）。

对于解决此题的常规方法学生都能轻松理解，但对于“200×3”这一算法并不是大部分孩子所能理解的。于是，我让学生当“小讲师”，采用边讲解边画图的策略（如图2），扫除了学生认知上的疑点和难点，体会到“积的变化规律”在此题中的巧妙运用。学生在“质疑→解疑→画图→理解”中，“化隐性为显性”，不仅能有效地培养数感，也能促进学生数学思维的发展。

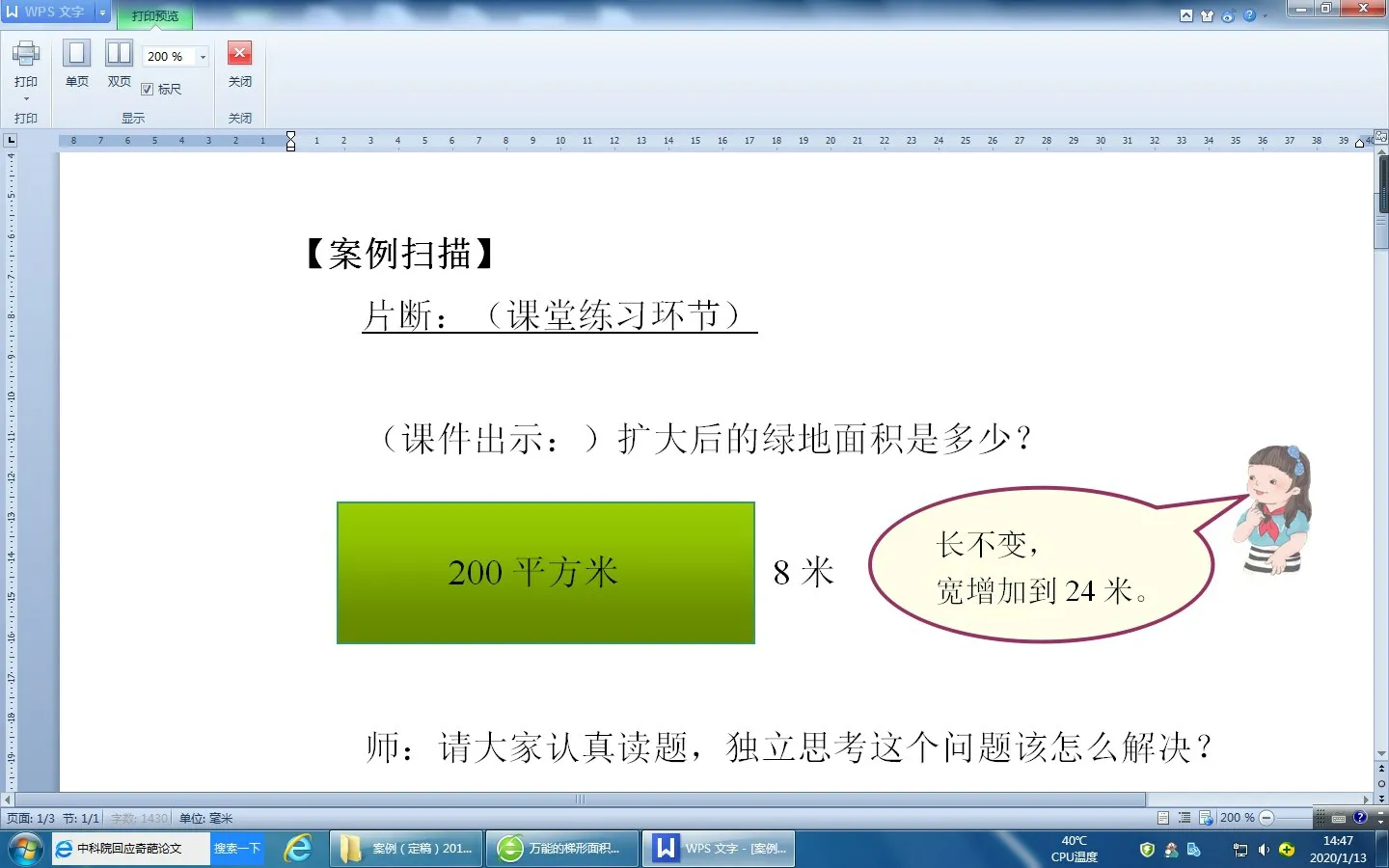
图1

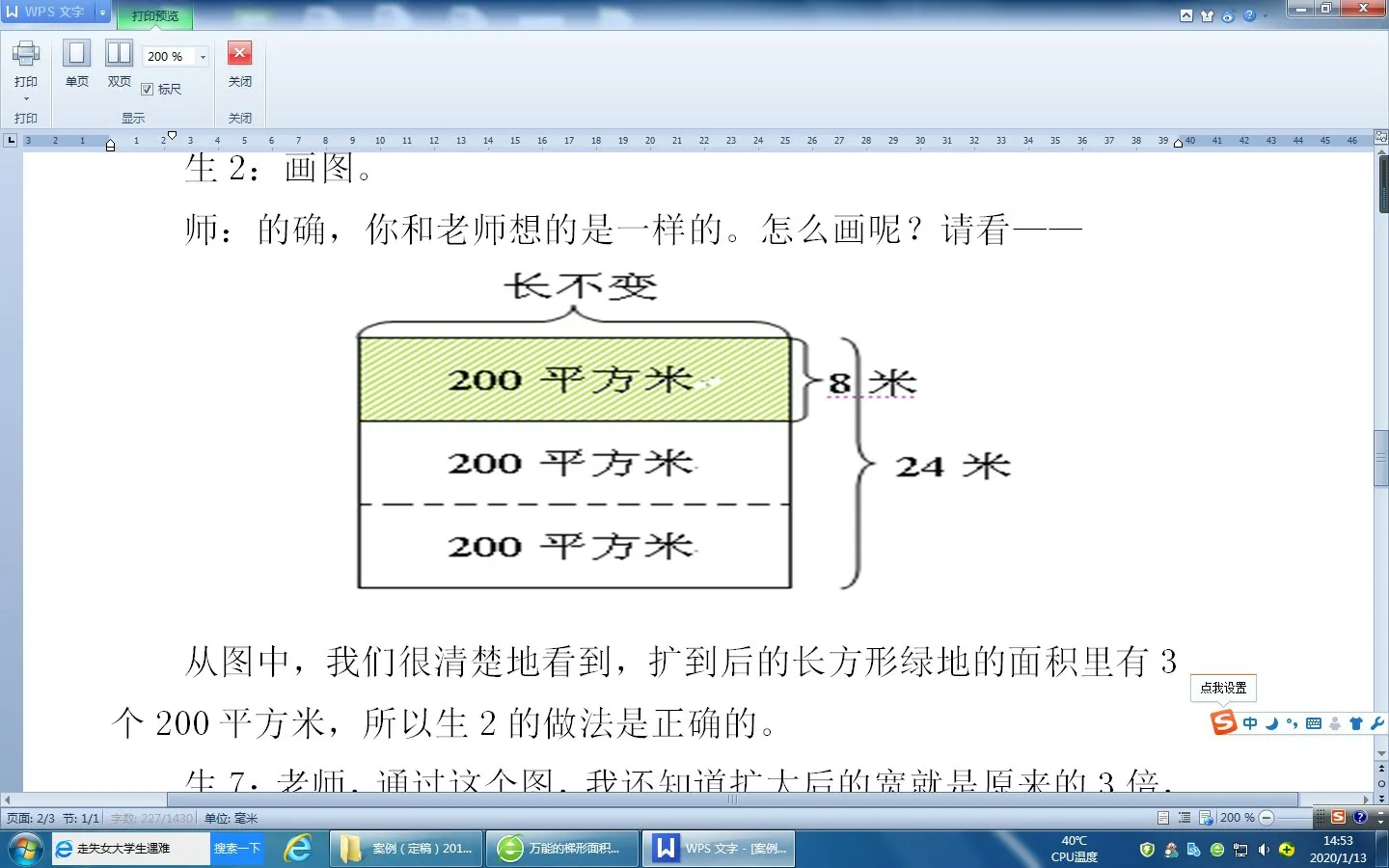
图2

（二）文化拓展，让学生体会数学之美

数学的生活化决定了数学不仅仅是一门抽象的学科，它应该也是一种文化。倘若教师在备课中能多一双慧眼，去留心生活，挖掘其潜在的文化因素，将会为数学课堂增色不少。例如，在学习《垂直与平行》时，在课末的欣赏环节，教师可以结合生活中的例子，进一步感受到数学与生活的密切联系，感悟到垂直与平行的运用价值。同时，教师在学生对“赏”的惊呼声中可以引导学生谈谈感受：“看了这些图片与视频，你有什么想说的？”“太美了！”“太震撼了！”“原来垂直与平行可以创造出这么多美好的事物。”……的确，培养学生对美的感悟，我想咱们数学学科也应该承担起义不容辞的责任。美，无处不在。这种对文化的拓展，在一定程度上让学生爱上数学，美育之花在孩子心中早已盛开。

总而言之，在小学数学课堂教学中，教师要能以引导者、引领者的身份来组织教学，并依据教学活动的状况和情势，迅速地做出判断，有效地跟进指导，把握引导的每一处“火候”适时地“煽风点火”，使课堂教学向纵深处发展，从而实现教师教与学生学的和谐统一。