长期反复荷载作用下软黏土地基的变形特性
师旭超,孙运德,士贺飞
(河南工业大学 土木建筑学院,郑州 450001)
随着经济的不断发展,在软黏土地基上的工程建设越来越多,如油罐、筒仓、港口集装箱堆场等。地基在运营期间承受长期反复荷载作用,由于荷载情况复杂多变,载荷波动较大,地基经常会出现变形大、沉降时间长且难于预测等问题。许多学者根据其实际变化规律进行统计分析,将实际荷载进行数学化,等效为有规律的加载类型,Rahal等[1]通过将筒仓荷载等效为正弦波载,对意大利的Ca’Mello筒仓进行了固结分析;Fattah等[2]通过试验发现,在松散砂土中,循环荷载作用下的沉降随着荷载速率的增加而增加,而在致密砂土中,循环荷载作用下的沉降随荷载速率的增加而减小;Yazdani等[3]推导了软黏土在循环荷载作用下的非线性固结解;Razouki等[4]求解了半正矢循环荷载作用下的一维固结解;Fujiwara等[5]通过现场观测研究了筒仓在满仓和空仓下地基的变形规律;Abbaspour[6]通过数值和试验分析了三角形循环荷载下的固结过程;徐至钧等[7]等通过长期观测实例油罐分析反复荷载下地基的沉降规律;有些学者通过试验对反复荷载下软土的变形规律进行了分析[8-12];杨峻等[13]运用荷载及微分方程的Laplace变换求解了双层地基反复荷载下的固结解;洪辉煌[14]用ABAQUS的修正剑桥模型模拟软土的固结变形,发现模拟值与试验值很接近;费康等[15]介绍了ABAQUS在岩土工程中的具体应用。
目前,对反复荷载下软黏土地基的长期沉降预测的研究较少。笔者基于太沙基一维固结理论,通过工程实例,利用ABAQUS有限元软件提出了一种反复荷载作用下软黏土地基长期沉降预测方法,并将实际监测与数值模拟进行对比,验证了该方法的合理性。
1 反复荷载作用下软黏土地基一维固结解
1.1 矩形反复荷载下一维固结解析解
矩形反复荷载为间断性施加的荷载,其数学公式可表示为
(1)
式中:T为加载周期;T1为加载时间段;N为加载周期数。
矩形荷载下的固结理论假设与太沙基固结理论相同。取任意深度一微元体为研究对象,假设渗流符合达西定律,则用有效应力表示的矩形反复荷载下的一维固结微分方程为
(2)
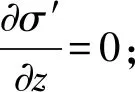
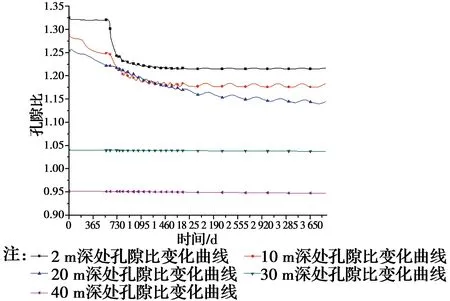
当NT (3) 式中:t1为加载时间段时间参数,0≤t1≤T1;T为累计时间参数,t=NT+t1。 当NT+T1 (4) 梯形荷载的数学表达式为(5)。 (5) 式中:qu为反复荷载;βt0为一个周期;α、β为加载系数;N为加载周期数;t0为在一个周期内到卸载结束时所用时间。 梯形反复荷载下的一维偏微分方程为 (6) 通过拉氏变换、逆变换及其时移性质,可以求解式(6)的解析解为 当(N-1)βt0≤t≤[(N-1)β+α]t0时 (7) 当[(N-1)β+α]t0≤t≤[(n-1)β+(1-α)]t0时 (8) 当[(N-1)β+(1-α)]t0≤t≤[(N-1)β+1]t0时 (9) 当[(N-1)β+1]t0≤t≤Nβt0时, (10) 文献[7]中一储油罐工程有数十年的沉降观测记录,该油罐位于河道附近,地势低洼,场地下方土层为高压缩性软土,地下水位埋藏深度为0.8 m,自上而下有6层土类组成,每层土体的参数见表1。表层土为河道吹填土,含水率及承载力很差,第3层土为压缩性非常高的软弱下卧层。该油罐直径为40.63 m,高度为16 m,油罐下边缘设1.7 m的透水性砂垫层,为了减少油罐的底部在反复荷载下的下陷程度,将地板预留为3.5%的拱度,中心最高处为2.4 m,用钢筋混凝土环墙约束砂垫层。采用两次充水预压,两次预压时间共计2 a,从第2次充水预压结束的第10天开始投产进油,投产观测时间为8.8 a,投产后的前两年半平均荷载峰值181.5 kPa,投产前两年半由于地基沉降的不稳定性,油面短时间内变化较大。 表1 土体的物理力学指标Table 1 Physical and mechanical indicators of soil 利用ABAQUS有限元软件进行建模[15],由于圆形油罐的对称性,可以取油罐的一半进行建模分析,采用二维。为减小边界条件的影响,取模型宽100 m、深80 m,考虑渗流与固结的耦合,选择CPE8RP单元类型。排水条件为顶部排水,本构模型选用修正剑桥模型。经过分析,前两年半内的荷载变化周期为两个月。后续储油周期大约达到了一年一个周期,荷载峰值基本保持在173.5 kPa。在观测的整个运营周期,考虑到油罐的自重及油面恒大于0,设置了大小为60.9 kPa的恒载。利用ABAQUS提供的DLOAD荷载自定义子程序,编制了自定义反复荷载。 该模型共设6个分析步,第1步为地应力平衡及预加先期固结压力;第2步为第1次充水预压,时间1.58 a;第3步为第2次充水,时间0.5 a;第4步为一持续时间为10 d空罐时间;第5步为投产后2.867 a,荷载周期为3个月的分析步;第6步为达到稳定运营之后6 a多的分析步,荷载周期为1 a。根据运营期的荷载峰值及变化频率,将荷载做了如图1中梯形荷载的近似,并作矩形荷载与恒载用于对比分析,图2为模型的数值模拟图。 图1 软件输出的荷载Fig.1 Output loadof software 图2 数值模型图Fig.2 Numerical model diagram 基础沉降云图如图3所示,从图3可以看出:储罐基础沉降云图大致为半个蝴蝶形状,地基中部沉降大、周边沉降小;基底压力沿深度逐渐向外扩散,导致下部土体发生径向位移,在基础边缘8.357 m以外土体向上隆起,最终隆起量为8.146 cm。隆起原因一是下部土体的径向位移侧向挤压土体,二是由于孔隙水压力的作用。 图3 竖向位移等值云图Fig.3 Vertical displacement equivalent cloud map 从图4可以看出,反复荷载下的沉降曲线与实测曲线有较好的吻合性;矩形荷载沉降大于梯形荷载,这是因为矩形荷载的水平加载时间段长于梯形荷载。由此可知,水平段的长短对结果的影响非常明显,随着周期数的增加,差距愈加明显,从图5也可以看出这一现象,因此,在进行实际荷载拟合时要充分考虑这一点。 图4 地基10 a沉降模拟、理论及实测值对比Fig.4 Comparison of foundation settlement simulation, theory and measured values for 10 years 图5 地基50 a沉降模拟值与理论值对比Fig.5 Comparison of simulated and theoretical values of 50-year settlement of foundation 表2显示图4的具体数值对比,由表2可以看出,实测的平均值为1.184 m,梯形反复荷载模拟的平均值为1.208 m,误差仅为2.07%,而恒载模拟的结果与实测相差较大,达到21.37%。但两者模拟结果都大于实测,这是由于实际荷载变化的随机性,等效后的荷载并不能与实际荷载完全吻合。通过对比可以发现,将荷载等效为梯形反复荷载较恒荷载有较高的真实性。从理论值、模拟值与实测值对比可以看出:模拟值误差比理论值普遍要小,这是由于理论公式的参数往往取平均值,不能像模拟那样分层准确取值;理论计算虽然不能像模拟那样能准确预测每一时刻具体变化(如图4中前期理论值误差很大),但是理论值与模拟值有相同的变化规律,也可以进行有效预测,并且理论计算比模拟更加方便快捷。 表2 投产10 a后各荷载沉降与实测对比Table 2 Comparison of load settlement and actual measurement after 10 years of production 从图5运营50 a的分析可以看出:地基在运营期间一直发生着沉降,土体的次固结将持续很长时间,但沉降速率很小而且均匀,不会对储罐设施造成破坏。从模拟值与理论值的对比可以看出,长期情况下理论值趋于稳定不变状态,模拟值处于缓慢沉降状态。这是由于土体的性质造成的,也说明理论解的局限性,通过实际情况可知,剑桥模型的模拟结果要比理论解更符合实际,而且更加可靠。 由图6可知,反复荷载值的大小对沉降的影响很大。实际反复荷载值作用的沉降为1.230 m,而当反复荷载值为100 kPa时的沉降为0.984 m,荷载相差20 kPa,沉降差值为0.246 m。因此,在将实际荷载进行拟合时,反复荷载值的大小是一个影响沉降的重要因素,应精确选择。 图6 不同荷载峰值下的地基沉降Fig.6 Foundation settlement under different load 由图7可以看出,反复荷载模拟沿深度的沉降值与实测值较贴近,第1层与第2层土体的沉降曲线比较吻合,第3层土体为软弱土层,沿深度有较大的沉降差。土层的沉降在40 m深处已经很小,实测值的影响深度在36 m处只有3.9 cm,然而,数值模拟中,沉降影响深度比实测值要深很多,在土层60 m深处也有4 cm的沉降量。所以,在建立模型时应设置足够的深度及宽度,以减小边界条件对模拟结果的影响。 图7 地基深层土体变形模拟及实测值分布图Fig.7 Simulation of deep soil deformation and distribution 从图8可以看出,在长期反复荷载下,孔隙水压力最终会围绕0值上下波动,并逐渐趋于某一个上下限数值,这个数值与荷载有关,孔隙水压力波动范围的稳定性与有效应力有关,即当有效应力稳定时,孔压波动范围也就稳定下来;有效应力随时间逐渐增加,渐渐趋于反复荷载值,其增加速率与土层深度和加载次数有关,随着深度的增加,有效应力受反复荷载的影响越小,在40 m深处的有效应力受反复荷载的影响已经很小,但50 a内仍在增加,而2 m深处的有效应力在投产两年后就基本达到了最大值,随着加载次数的增加,有效应力逐渐趋于稳定并随荷载变化,土体逐渐显现出来弹性的特性。 从图8中梯形荷载下理论孔压值与模拟孔压值对比可知,理论孔压值变化的幅度大于模拟值,这也解释了图4和图5理论沉降再加卸载时的变化幅度大于模拟沉降的原因,但两者有相似变化规律,从而论证了推导的固结解的正确性。 图8 运营50 a后不同深度有效应力及孔压随时间变化曲线Fig.8 Curve of effective stress and pore pressure with time at different depths after 50 years of 从图9可以看出,有效应力随着时间逐渐增大,在运营期间,随着反复次数的增加,塑性应变逐渐减小;在2.5 a以后,每个加载周期塑性应变的增加量已经很小,可以说地基沉降已经进入了稳定增长期;随着深度的增加,反复荷载对有效应力-应变曲线影响越小,在30 m深处曲线基本变为线性增加。 图9 运营10 a后土层深处有效应力-应变曲线Fig.9 Effective stress-strain curve in the depth of soil after 10 years of operation 由图10可知,土层越浅孔隙比前期变化速率越快,达到稳定孔隙比的时间越短;在预压结束后,孔隙比均已经减小到了稳定值;土层越深孔隙比变化速率越均匀,达到稳定孔隙比所需时间就越长,如20 m深处的孔隙比变化;随着土层深度的增加,孔隙比受反复荷载的影响越来越小,如30 m深处的孔隙比受反复荷载的影响效果比较浅处土层要小很多,其在运营周期内的变化非常微小。 图10 梯形荷载下不同深度孔隙比变化曲线Fig.10 Curve of variation of void ratio at different depths under trapezoidal load 1)基于太沙基一维固结理论,推导出了矩形及梯形反复荷载作用下软土地基的一维固结解析解。 2)通过利用ABAQUS有限元软件及相关自定义子程序,对实例油罐荷载按照等效反复荷载作用和恒载作用分别进行了沉降数值模拟,发现对于储罐类受反复荷载作用的软土地基,利用反复荷载进行数值模拟的结果比恒荷载要精确很多,且与实测值相比误差很小。 3)通过对存储类型、储量及储存周期的预先分析,可以近似确定等效反复荷载类型及大小,进而进行准确的数值模拟,其模拟结果不仅可以对存储类地基长期沉降进行预测,也可以得到实测中一些无法得到的数据,如土体形变、孔隙水压力及孔隙比对荷载的响应等,还可以辅助实地观测进行地基的承载力及差异沉降分析。 4)反复荷载的水平加载段时间与荷载值对地基的长期沉降影响明显,水平加载段越长、反复荷载值越大,沉降量越大;反复荷载下有效应力随着加载次数其总体趋势逐渐增加;随着土层深度的增加孔隙比的变化受反复荷载的影响越来越小。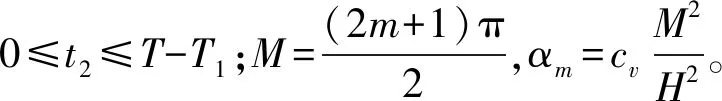
1.2 梯形反复荷载下一维固结解析解

2 工程实例及模型
2.1 工程实例

2.2 模型建立及模拟方法



3 软土地基变形分析
3.1 地基沉降变化规律




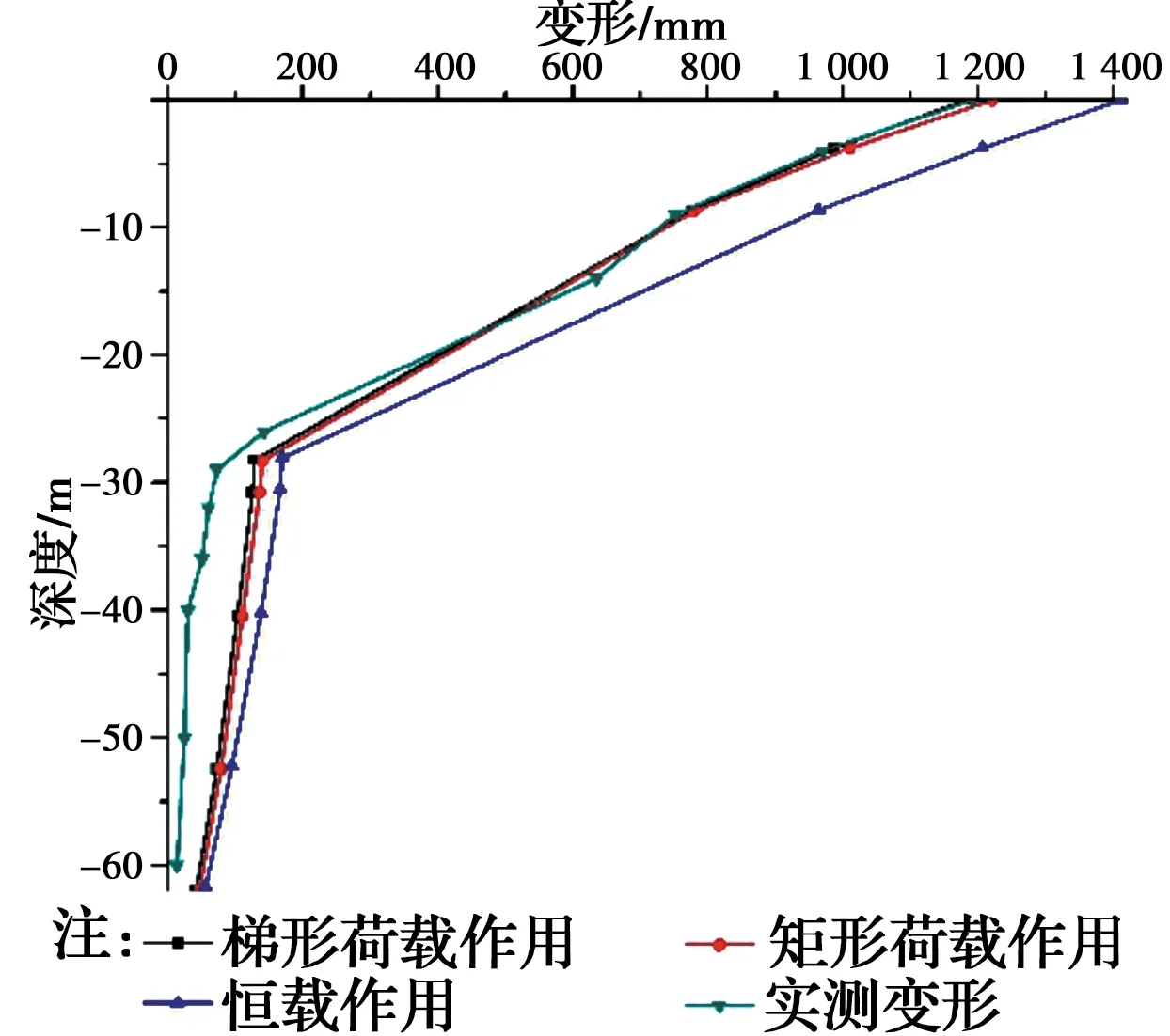
3.2 孔隙水压力与有效应力变化规律

3.3 有效应力-应变关系变化规律
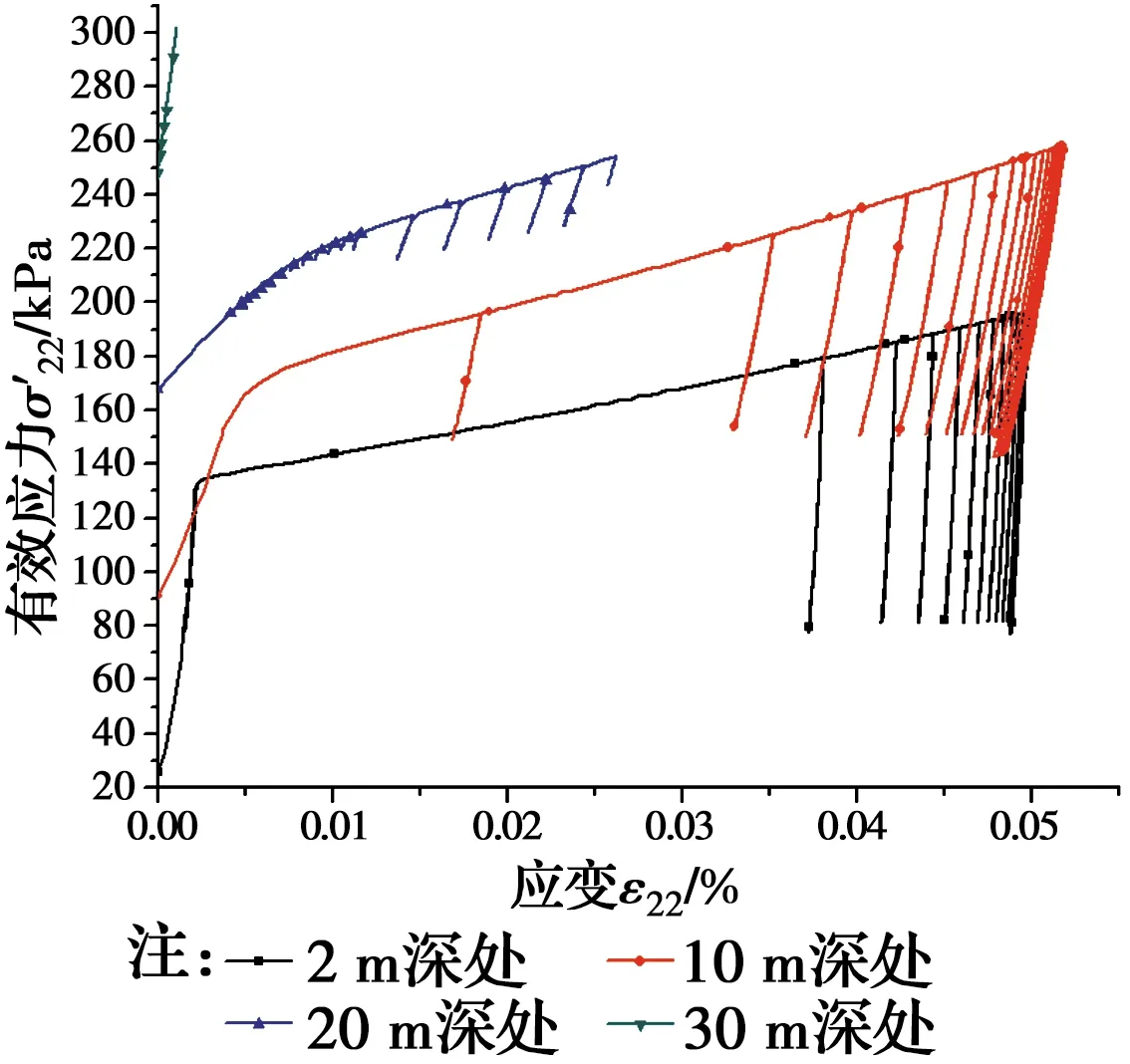
3.4 孔隙比变化规律
4 结论

