基于BP神经网络模型的昌江流域洪水预报

钟 聪，王永文，2，刘卫林，2，吴美芳，程永娟

(1.南昌工程学院 水利与生态工程学院，江西 南昌 330000；2.江西省水文水资源与水环境重点实验室， 江西 南昌 330000；3.景德镇市水文局，江西 景德镇 333000)

洪水预报是防洪非工程的关键措施之一，其预报精度对水利工程的调度运行和防洪救灾的实施有着重大影响[1]。洪水预报应用传统的预报方法之外，还可以采用人工神经网络模型进行洪水预报。神经网络模型在洪水预报中有着广泛的应用[2]。金保明等[3]应用了基于反向传播算法的神经网络模型对闽江支流崇阳溪流域进行洪水预报；刘欢等[4]进行了基于BP神经网络模型的河道洪水反向演算研究；王竹等[5]根据大伙房流域特点提出了一种半分布式BP神经网络洪水预报模型。该模型本质上是一种“黑箱”统计模型[6]，通过控制变量法率定BP人工神经网络的参数，结果表明可以获得一个较好的预报精度[7]。昌江流域目前采用的仍然是传统的洪水预报方法，即新安江模型和马斯京根模型，但是，由于流域内在2019年新建成了浯溪口水利枢纽工程，改变了流域水文特性，需要重新调整水文预报模型。因此，本文构建了人工神经网络模型，以昌江流域为例验证了该模型在一定程度上具有准确性和实用性。

1 研究区域概况

昌江主河道长254.0km，东北邻新安江、秋蒲河、青弋江，西毗潼津河，南靠饶河，似扇形。浮梁县境内的潭口水文站以上为上游，潭口水文站至景德镇市城区内的渡峰坑水文站河段为中游，渡峰坑水文站以下至鄱阳县姚公渡为下游。

2 BP神经网络模型的原理

人工神经网络模型通常由输入层、输出层和隐含层组成， 通过学习和训练一定数量的样本， 确定模型相关参数，正向信息传播和反向误差传播这两个交替迭代过程构成了神经网络的学习过程[8]。正向传播时，样本由输入层经过隐层计算后传递到输出层。输出值与预设值经过比较后，如果其误差大于设定值时，误差的反向传播阶段开始执行。反向传播时，输出误差将以特定方式传播到隐层和输出层，各连接之间的阈值和权值得到不断修正。网络的训练学习过程就是这种信号的正向和反向传播过程。网络的输出误差在预设值之内或训练次数达到预设次数之前重复进行，当网络训练结束后，采用导出的代码进行预测。研究表明一个3层的BP神经网络可以实现任何复杂的映射问题[9]，所以选择3层结构的神经网络模型，如图1所示。

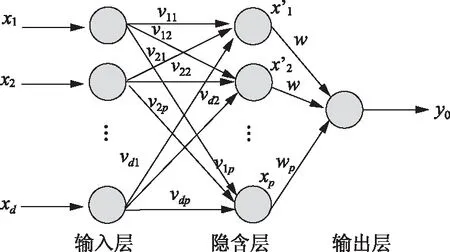
图1 神经网络三层模型

BP算法的实现过程如下：

设h、i、j依次是输入神经元、隐层神经元和输出神经元，每层的节点数目依次是nh、ni和nj，隐层节点i和输出层节点j的阈值依次是θi和θj，隐层节点i和输入层节点h间的权值是whi，输出层节点j和隐层节点i间的权值是wij，x和y依次是每一个节点的输入和输出。

第一步：初始化。设下列样本是归一化之后的输入、输出样本

{xk，h，dk，j|k=1，2，…，nk；h=1，2，…，nh；j=1，2，…，nj；}

(1)

nk是样本容量。将(-1，1)区间上的随机数值赋给各连接权{whi}、{wij}和阈值{θi}、{θj}。

第二步：置k=1，网络(h=1，2，…，nh；j=1，2，…，nj) 收到样本对(xk，h，dk，j)。

在利益相关者的权力意识不断觉醒时代，分权是高等教育管理的趋势，我国正在致力构建高等教育治理能力和治理体系的现代化，作为其中一环，我国高等教育分权改革也随着国家治理范式的转变逐渐走向公开化、法治化和问责化。

第三步：隐层各节点的输入xi、输出yi(i=1，2，…，ni)的计算

(2)

yi=1/(1+e-xi)

(3)

第四步：对输出层中每个节点的输入xj和输出yj进行计算，其中(j=1，2，…，nj)

(4)

yj=1/(1+e-xj)

(5)

第五步：计算总输入变化时输出层各节点所收到的单样本点误差Ek的变化率

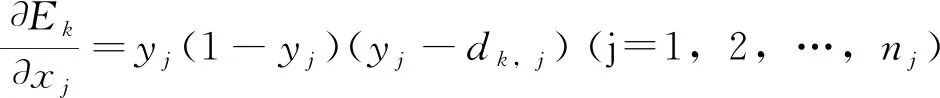
(6)

第六步：计算总输入变化时隐层各节点所收到的单样本点误差的变化率

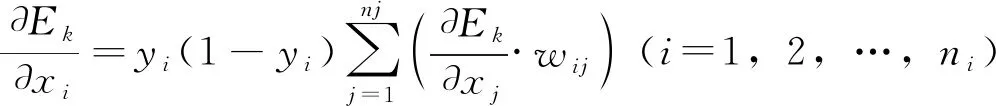
(7)

第七步：各连接的权值和阈值的修正

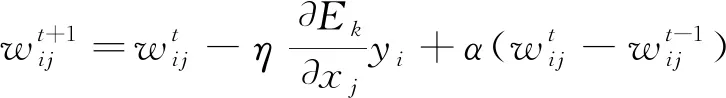
(8)

(9)

(10)

(11)

式中，t—修正次数，学习速率η∈(0，1)，动量因子α∈(0，1)。当η相对大时，算法迅速收敛，但是也许会产生不稳定的情况；当η相对小时，算法收敛可能相对慢一些；α和η的效果相反。

第八步：置k=k+1，网络收到学习模式对(xk，h，dk，j)，跳到第三步，直到训练完全部nk个模式对，跳到第九步。

第九步：重复第二步到第八步，直到网络全局误差函数

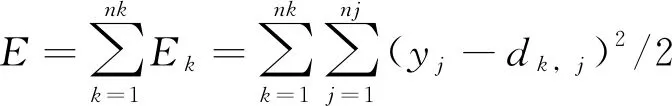
(12)

比之前假定的一个较小值要小或学习次数比预先设定的值要多时，学习完成。

3 实例应用

3.1 BP人工神经网络模型的建立

本文拟构建基于BP神经网络的洪水预报模型，提前3h预报昌江渡峰坑水文站洪水。选取流域面平均雨量和上游浯溪口洪水过程为输入变量，干流下游渡峰坑水文站相应洪水流量为输出，采用最速下降动量反向传播算法建立渡峰坑水文站洪水流量预报模型。由于浯溪口刚刚建成，缺乏实测水文数据，暂时采用下游距离不远的樟树坑的水文数据代替。采用2016—2017年的14场洪水资料对所构建的神经网络模型进行训练率定参数，然后利用训练好的神经网络模型对2018年与2019年洪水过程进行预报。

3.2 神经网络模型参数的率定

通常对输入层、隐含层和输出层进行设计，即对网络层数的选择、各层神经元数的选择、各层激活函数的选用等来确定BP 网络结构[10- 12]。采用matlab软件自带的神经网络时间系列工具箱来训练人工神经网络。根据洪水预报的特点，选择Nonlinearinput-output结构。在有机器的监督学习中，通过尝试，把数据集分为3部分，分别为70%的训练集，15%的验证集，15%的测试集。隐含层节点数的选择并没有行之有效的方法，可通过试错法进行选择。通过多次尝试，当隐含层节点数取为11时，训练效果较好。考虑到流域实际情况，预见期取3个时段时效果较好。神经网络训练算法采用Levenberg-Marquardt算法，它具有牛顿法与梯度法的优点，收敛速度较快。其余参数采用神经网络工具箱默认的参数。

3.3 模型评价指标

在研究过程中，采用洪峰绝对误差绝对值、相对误差绝对值、峰现时间绝对误差以及确定性系数评价洪水流量预报模型的精度[13]，相应指标计算方法如下:

相对误差公式:

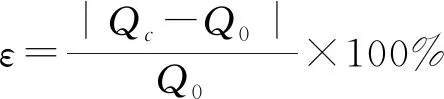
(13)

确定性系数公式：

(14)

绝对误差公式:

Δ=Qc-Q0

(15)

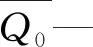
3.4 结果分析

采用2016—2017年的14场洪水资料作为检验样本模拟渡峰坑水文站的洪水流量过程，各场次实测和预测洪水流量过程线如图2所示，每场洪水的洪峰流量模拟及预报误差见表1。

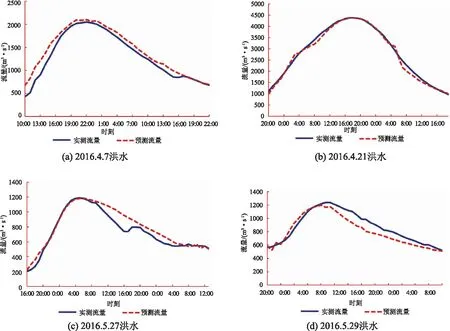
图2 渡峰坑洪水训练洪峰折线图

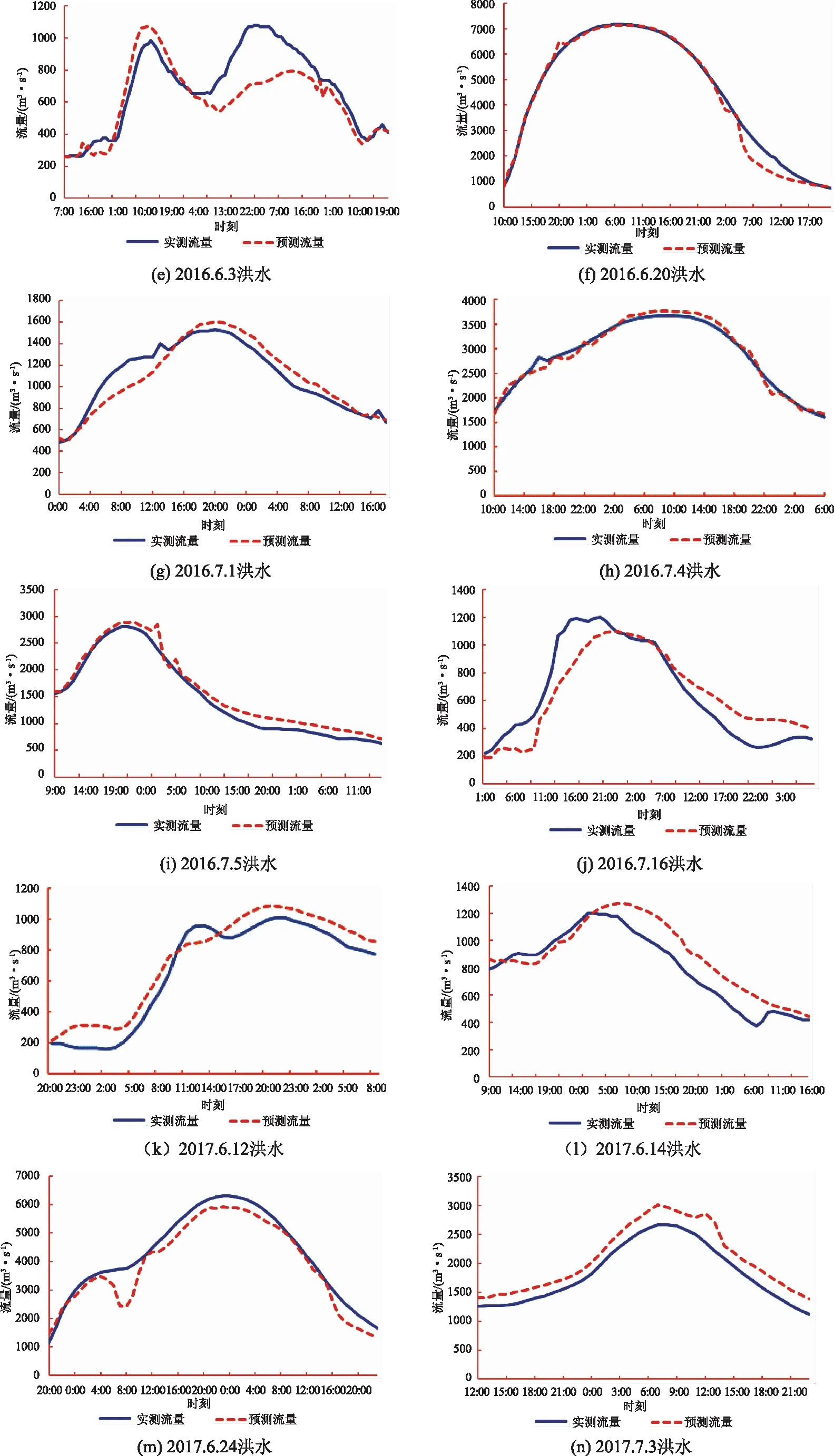
续图2 渡峰坑洪水训练洪峰折线图

表1 渡峰坑洪水训练统计表

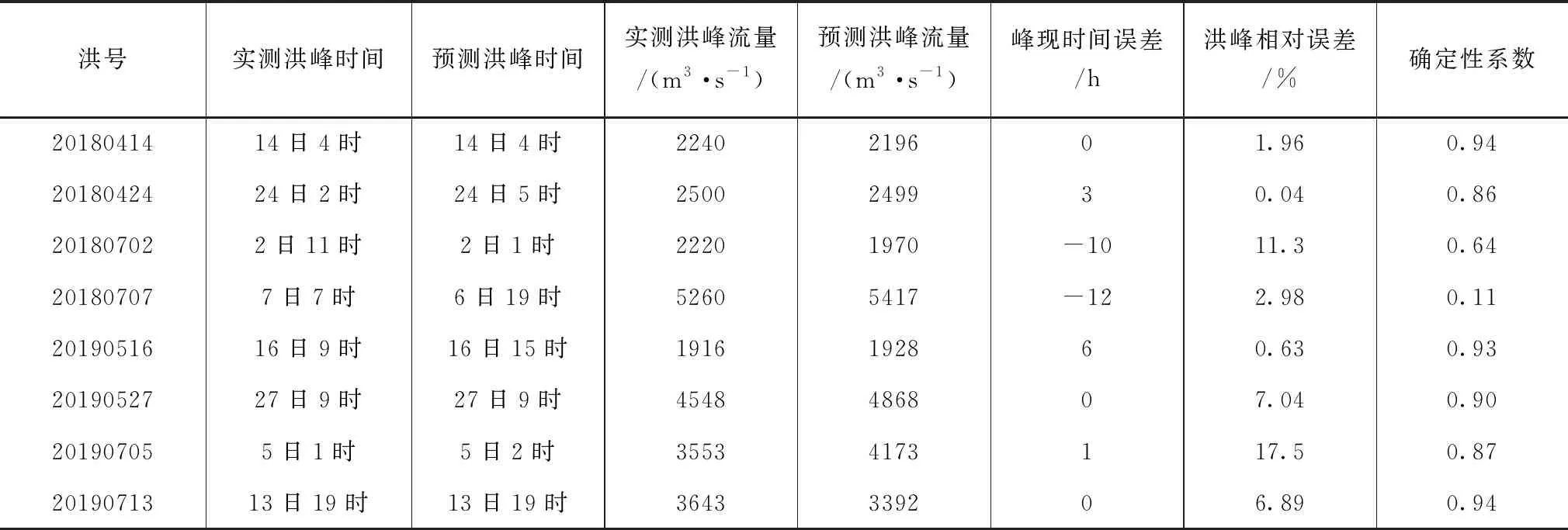
表2 渡峰坑洪水检验统计表

从图2和表1的14次洪水模拟结果来看，洪水过程模拟结果拟合度较好，只有1场洪水洪峰流量误差大于10%，但均在15%之内；有2场洪水峰现时间误差分别为36h和6h，其余均在2h以内，峰现合格率为86%。有1场洪水确定性系数小于0.7，合格率为93%。

参数率定后，利用所构建的神经网络预报模型对渡峰坑水文站2018年和2019年的洪水数据进行验证，验证期间径流量实测值与模拟值的拟合结果如图3所示，验证期模型适应性指标计算结果见表2。

根据图3与表2的8次洪水预测结果可知： 2018年4场次洪水检验中，只有20180702场次洪水洪峰模拟误差为11.3%，其余洪峰流量相对误差均在3%之内；有2场洪水峰现时间误差较大，分别为12h和10h。2019年4场次洪水检验中，有3场洪峰流量误差均在7%之内，但20190705场次洪水洪峰模拟误差为17.5%；201905161场次洪水峰现时间误差较大，为6h。总体上，2018—2019年8场次洪水除20180702和20180707场次洪水外，其余场次洪水模拟确定性系数均在85%以上，确定性系数检验有6场洪水合格。2场不合格均为2018年7月份的洪水，经分析，主要是浯溪口水利枢纽施工影响。

图3 渡峰坑洪水检验洪峰折线图

4 结论

本文以鄱阳湖昌江流域为研究对象，选取流域面平均雨量和其上游樟树坑水文站洪水过程为输入，渡峰坑水文站出流量为输出，建立渡峰坑水文站洪水预报BP神经网络模型。从模拟和检验结果来看，采用人工神经网络模型进行洪水预报时，渡峰坑水文站洪水过程模拟和检验效果较好，可作为传统预报方式的有益参考，但因昌江上游私人电站开启时间的不确定性，潭口与渡峰坑之间新建浯溪口水利枢纽的影响，预报峰现时间具有不确定性。