车用柴油机主轴承轴瓦微动磨损研究

谷冉升，崔毅,2，程祥军，李云强

(1.上海交通大学动力机械及工程教育部重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.潍柴动力股份有限公司，山东 潍坊 261001)

随着对柴油机使用寿命和功率密度要求的不断提高，发动机轴瓦过盈配合面由于承受很大的交变载荷，接触面上会有局部的微动磨损出现，进而导致表面裂纹的萌生和轴瓦失效[1-2]。Archard[3]基于Holm等提出的一种计算表面原子移除的磨损理论，用原子团代替单个原子将这个理论应用到了表面微凸体的移除。Archard认为磨损量主要与材料的硬度以及接触副上的正压力和滑移量有关。Archard模型提出后便被用于有限元仿真和磨损分析。J.Ding[4-8]等对圆柱-平面接触的微动磨损装置进行了仿真分析，用Archard模型对接触面轮廓的变化情况进行了预测，并研究了微动磨损对微动疲劳的影响。杜平[9]对简化结构的连杆-衬套进行有限元分析，利用Hertz理论研究连杆摆角、过盈量和摩擦系数对微动磨损的影响，发现加大过盈量可以显著减小滑移，并能提高使用寿命，降低摩擦系数可以降低总体摩擦功。张远斌[10]为研究车轮-车轴过盈面的微动磨损特性，对圆柱-平面结构进行仿真，结果表明，该模型可以较准确预测磨损斑的宽度，但对于磨损斑的深度仿真误差较大。高立[11]对连杆小头-衬套进行热固耦合仿真分析，得出温度升高使接触压力和摩擦应力显著增大的结论。过盈增大会使微动滑移距离减小，因此提高过盈并改善润滑条件可以很好地降低微动磨损。

本研究对一款车用柴油机搭建试验台架来探究不同预紧力下主轴承-机体过盈接触面的微动磨损，同时根据试验台架建立对应仿真模型，根据Archard模型获取仿真磨损结果并与试验结果相互验证，据此分析不同因素对微动磨损的影响，得到减小微动磨损的方案。

1 试验研究

1.1 试验台架

为了研究主轴承轴瓦瓦背的微动磨损情况，搭建柴油机1 000万次动载试验台架。柴油机主要参数见表1。试验台架由八部分组成：油槽、固定底座、主轴承盖、机体、主轴瓦、加工曲轴、固定法兰盘和双轴疲劳试验机。试验台架安装情况见图1，发动机内部安装情况见图2。为模拟曲轴的润滑条件，在试验加工曲轴上打油孔，使其能够对曲轴-轴瓦接触面循环供油。为分析不同螺栓预紧力对机体-主轴承结合面微动磨损的影响，试验对单段曲轴左右两组主轴承施加不同大小的螺栓预紧力。

表1 柴油机主要参数

1—双轴疲劳试验机；2—固定法兰盘；3—被试柴油机；4—固定底座；5—油槽。图1 试验台架结构

1—机体；2—加工曲轴；3—主轴瓦；4—主轴承盖。图2 被试柴油机内部结构

图1和图2中，固定底座通过两排螺栓孔与机体进行螺栓连接，起到固定和定位的作用；法兰盘用于连接曲轴和疲劳试验机；开供油孔的曲轴两侧均有进油孔，并在两个上轴瓦中心45°位置设出油孔；曲轴、供油管道、油槽和油泵组成的润滑系统，保证了轴-轴瓦接触面循环供油。

1.2 试验方案

标定工况下主轴承载荷见图3。由于曲轴和轴瓦存在间隙，在轴承载荷换向时疲劳机载荷无法控制，因此试验加载频率无法提升。为提高试验频率，试验最大载荷和实际工况一致，改变最小载荷大小，使主轴处于单向加载状态。按照这种方式对实际载荷的修正对下轴瓦的微动磨损影响不大。试验机的加载参数如表2所示。

图3 主轴承载荷x,y分量

表2 试验加载参数

加载频率的选取是综合考虑疲劳试验机加载稳定性和试验总时间得到的。30 Hz的加载频率能保证正弦加载的稳定性，同时尽可能缩短试验时间。

两组主螺栓施加不同的预紧力，施加方式为转角法。其中飞轮端(左侧)螺栓拧紧力矩为厂家提供的最大拧紧力矩，自由端(右侧)是根据最大拧紧力矩进行减小得到的。

0.5 MPa的机油压力是模拟发动机实际运行时的主轴承供油压力，曲轴与轴瓦间的持续供油润滑可以防止曲轴-轴瓦接触面因高速摩擦过热而烧结。

1.3 试验结果分析

试验结束后，取下轴瓦，可以观察轴瓦瓦背的微动磨损情况，如图4所示。

图4 轴瓦瓦背磨损结果

图4中，由于轴瓦瓦背上有磷化层，磨损状况不易观察，因此转而观察与其对应的接触面：机体-上轴瓦背接触面、主轴承盖-下轴瓦背接触面的微动磨损情况。图5示出两个机体-上轴瓦背接触面的磨损情况；图6示出两个主轴承盖-下轴瓦背接触面的磨损情况。

图5 机体-上轴瓦背接触面的磨损情况

图6 主轴承盖-下轴瓦背接触面的磨损情况

图5和图6中，微动磨损会造成机体-主轴承结合面磨损严重区域出现黑色磨损斑，触摸会有轻微的凹陷感。

对比图5中左右两个机体-上轴瓦背接触面的磨损情况，发现飞轮端(左侧)接触面磨损较严重，右侧接触面磨损斑不明显，但出现凹坑，原因是右侧预紧力小，接触面在试验过程中有分离现象，部分金属黏着脱落。磨损严重位置集中在两侧边缘30°区域。

对比图6中左右两个主轴承盖-下轴瓦背接触面的磨损情况，发现自由端(右侧)的磨损更严重，磨损严重位置集中在接触面的中心位置到45°角区域。磨损斑痕迹沿轴瓦周向分布。

2 计算研究

2.1 有限元模型

根据试验台架建立相对应的有限元模型(见图7)。模型共包含四部分：机体、2个轴瓦、4个主螺栓、2个主轴承盖。有限元模型中，对机体与主轴承盖、主轴瓦接触部分的网格进行剖分细化，提高关心区域的计算精度。由于模型存在大量非线性接触区域，网格类型均采用C3D10M四面体网格。网格模型总节点数为410 451。

图7 有限元网格模型

为简化计算，模型中不考虑曲轴，而是将载荷直接施加在轴瓦上。加载方式采用120 °分布式加载，如图8所示。

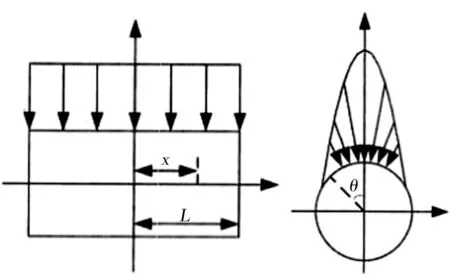
图8 主轴承载荷加载方法

如图8所示，主轴承载荷为沿主轴承轴向方向均匀分布，沿主轴承周向呈120°余弦分布。设竖直方向的总载荷为Q，轴向受力长度为L，轴颈半径为R，推导过程如下：

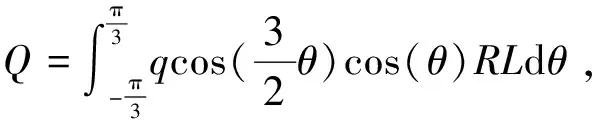
(1)

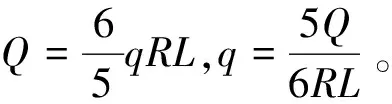
(2)

螺栓预紧力数值根据转角法计算得到，飞轮端(左侧)螺栓预紧力为88 kN，自由端(右侧)螺栓预紧力为78.9 kN。

2.2 微动磨损计算模型

微动磨损计算采用Archard模型：

(3)

式中：h为磨损深度；s为滑移距离；p为接触压力；kl为局部磨损系数。为了计算一个工作循环总的磨损深度，需要对一个工作循环中的有限元计算步进行累加：

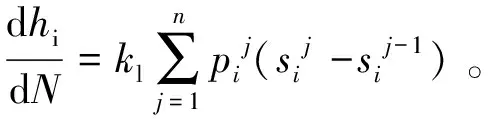
(4)

式中：N为工作循环数；pij，sij分别为第i个节点，第j计算步的接触压力和滑移量；dhi/dN为第i个节点一个工作循环的总磨损深度。

通过编程提取ABAQUS有限元分析结果中相关参数，并通过计算得到磨损深度h的分布，并以云图方式显示。

由于只分析磨损深度的相对大小，将磨损系数kl取为1。并将kl取1时的磨损深度h记为微动磨损参数FD。

2.3 计算结果与分析

首先分析与微动磨损参数FD计算相关的参数：接触压力p和滑移距离s。其中接触压力p可以直接从分析结果CPRESS中读出，滑移距离s通过编程来计算一个循环的总滑移量。计算方法如下：

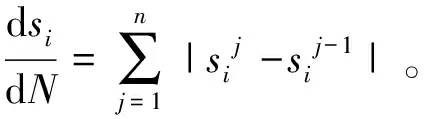
(5)

分析接触压力p时，选取压载荷5 kN和116 kN两种工况下接触压力更大的进行分析。由于机体-上轴瓦背接触面主要受螺栓预紧力影响，压载荷5 kN时接触压力p更大，因此选取压载荷5 kN工况(见图9)；而主轴承盖-下轴瓦背接触面的接触压力p主要受压载荷的影响，因此选取压载荷116 kN工况(见图10)。

图9 机体-上轴瓦背接触面5 kN时的接触压力

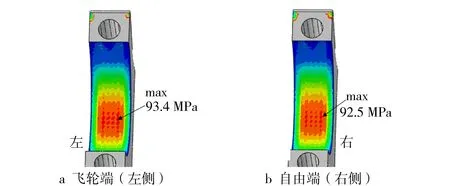
图10 主轴承盖-下轴瓦背接触面116 kN时的接触压力

根据计算得到的总滑移距离s绘制机体-上轴瓦背接触面滑移云图(见图11)和主轴承盖-下轴瓦背接触面滑移云图(见图12)。

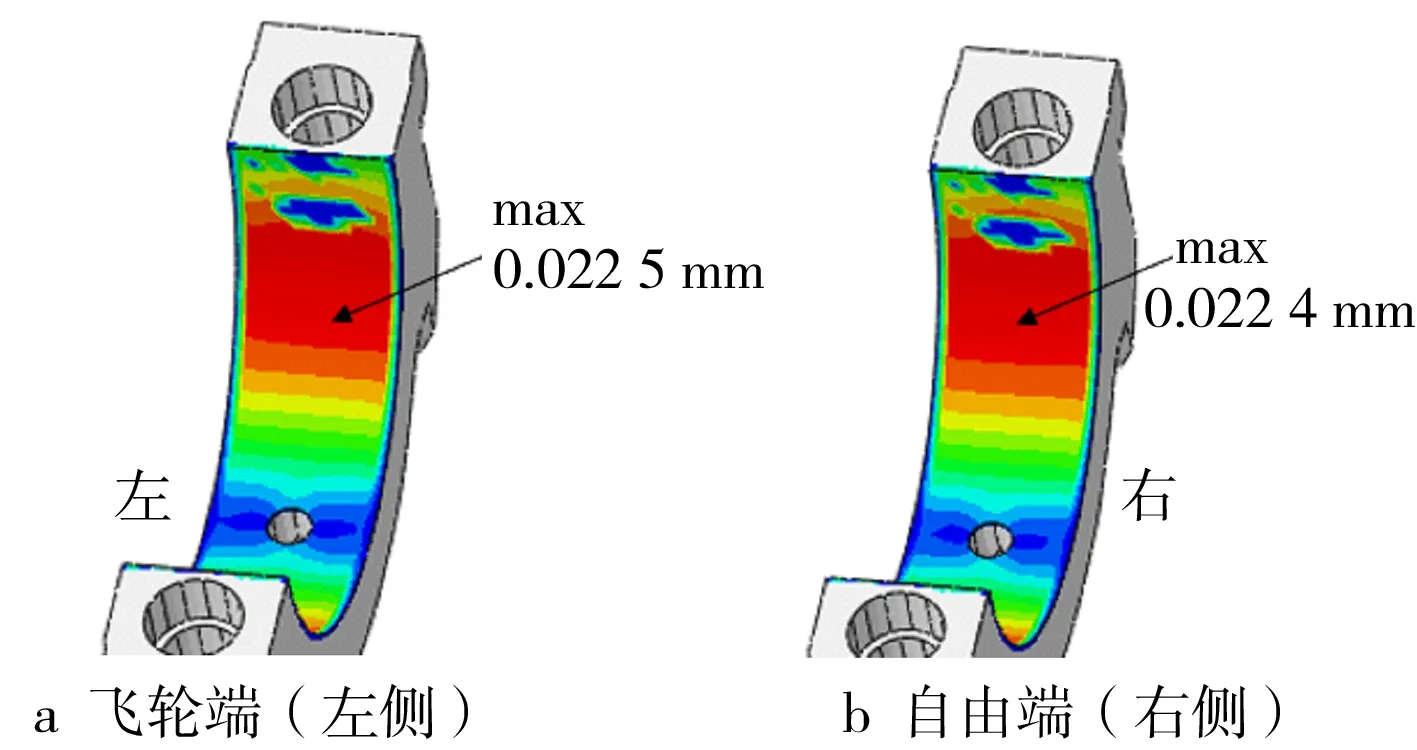
图11 机体-上轴瓦背接触面滑移距离

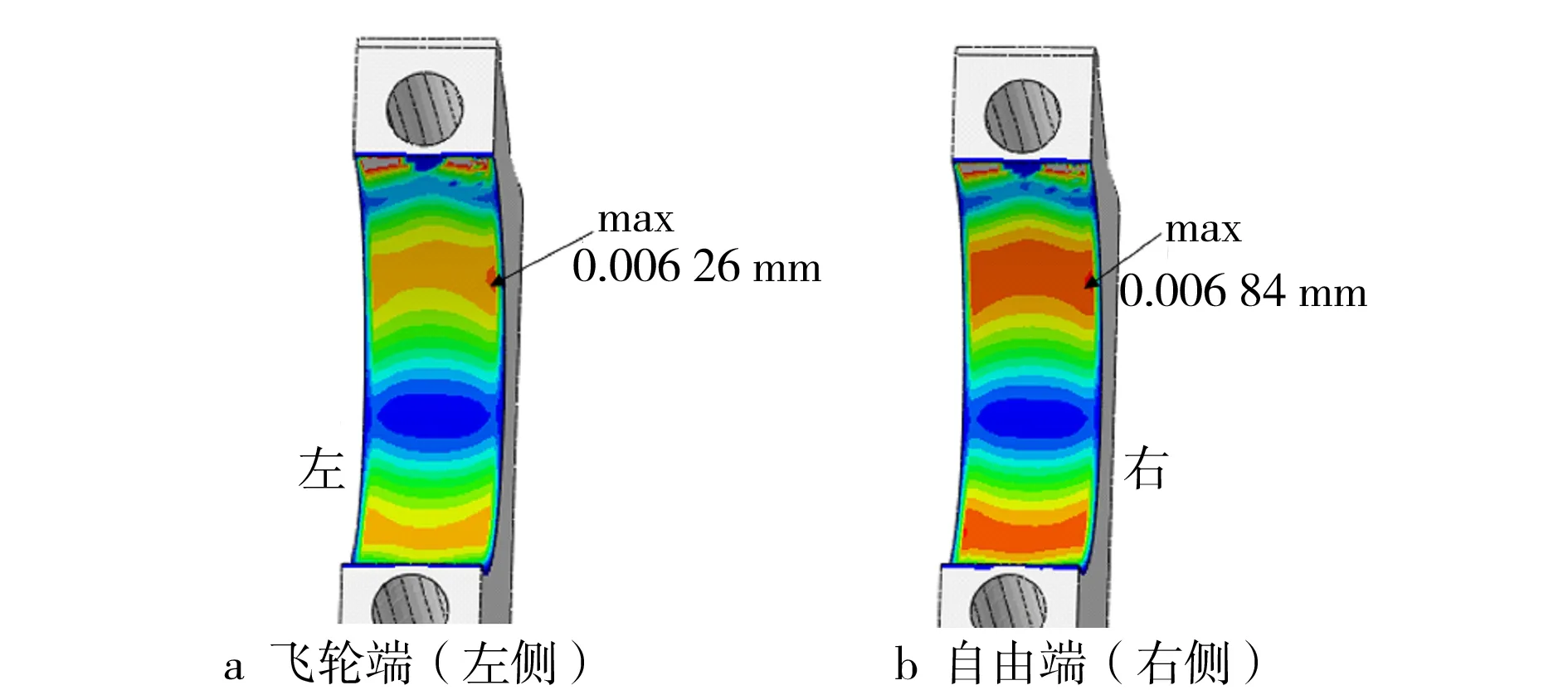
图12 主轴承盖-下轴瓦背接触面滑移距离

图13和图14示出了图5和图6对应位置单个加载循环的微动磨损深度云图。

图13 机体-上轴瓦背接触面的磨损仿真结果

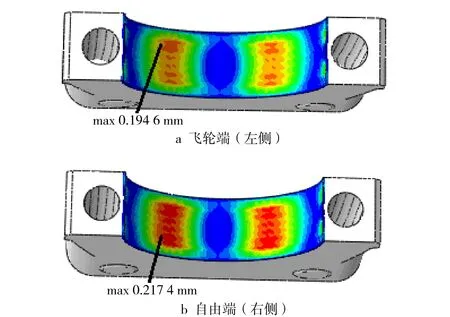
图14 主轴承盖-下轴瓦背接触面的磨损仿真结果

结合接触压力和滑移距离分析磨损结果，可见机体-上轴瓦背接触面磨损的分布情况与接触压力相近，原因是压载荷的变化并不会导致上轴瓦发生严重形变，所以机体-上轴瓦背接触面滑移距离不是影响磨损分布的主因，而由螺栓预紧力引起的接触压力分布是磨损的主要成因。这很好地解释了磨损严重位置集中在靠近螺栓头的接触面边缘到25°之间，也很好地解释了由于飞轮端(左侧)比自由端(右侧)螺栓预紧力大导致左侧比右侧磨损严重。仿真得到的机体-上轴瓦背接触面磨损情况从分布和螺栓预紧力对其磨损严重程度的影响上均与试验结果相吻合。

主轴承盖-下轴瓦背接触面磨损情况与滑移距离的分布相近，原因是压载荷直接作用在下轴瓦上，因此压载荷变化导致的下轴瓦形变会加大主轴承盖-下轴瓦背接触面在45°角附近的滑移距离，成为影响磨损分布的主因。更大的预紧力导致了更大的接触压力(见图10)，进而导致下轴瓦与主轴承盖之间更难发生相对滑动，减小了滑移距离(见图12)。由于数值上螺栓预紧力增加对滑移距离的影响更大，因此螺栓预紧力对磨损的影响与滑移距离的影响一致，即自由端(右侧)比飞轮端(左侧)磨损严重。仿真结果和试验结果较为吻合。

总体上，根据Archard模型得到的磨损深度仿真结果与试验得到的结果在预紧力对磨损影响趋势一致，同时磨损深度分布也比较吻合。

3 减磨优化分析

通过在有限元模型中调整螺栓预紧力和主轴承轴瓦过盈量寻找减小柴油机主轴承轴瓦微动磨损的方法。根据之前试验及仿真结果，可知上下轴瓦的磨损情况并不相同，因此对上下轴瓦分开分析。设初始轴瓦半径过盈量为a，分析结果见图15。

对于上轴瓦来说，随着轴瓦半径过盈量增加，瓦背微动磨损先增大后减小，在轴瓦半径过盈量为(a+0.01) mm附近达到峰值。螺栓预紧力增大会导致微动磨损增大，但是随着轴瓦半径过盈量增加，螺栓预紧力对上轴瓦微动磨损的影响减小，当轴瓦半径过盈量为(a+0.04) mm时，螺栓预紧力对微动磨损的影响几乎为零。因此，当轴瓦半径过盈量大于(a+0.01) mm时，增加过盈量可以减小上瓦背磨损。

对于下轴瓦来说，轴瓦半径过盈量与瓦背微动磨损成反比。螺栓预紧力与瓦背微动磨损也成反比。因此，增大轴瓦半径过盈量和螺栓预紧力均能减小下瓦背磨损。

综上，当轴瓦半径过盈量大于(a+0.01)mm时，增大轴瓦半径过盈量可以很好地减小上、下瓦背磨损。

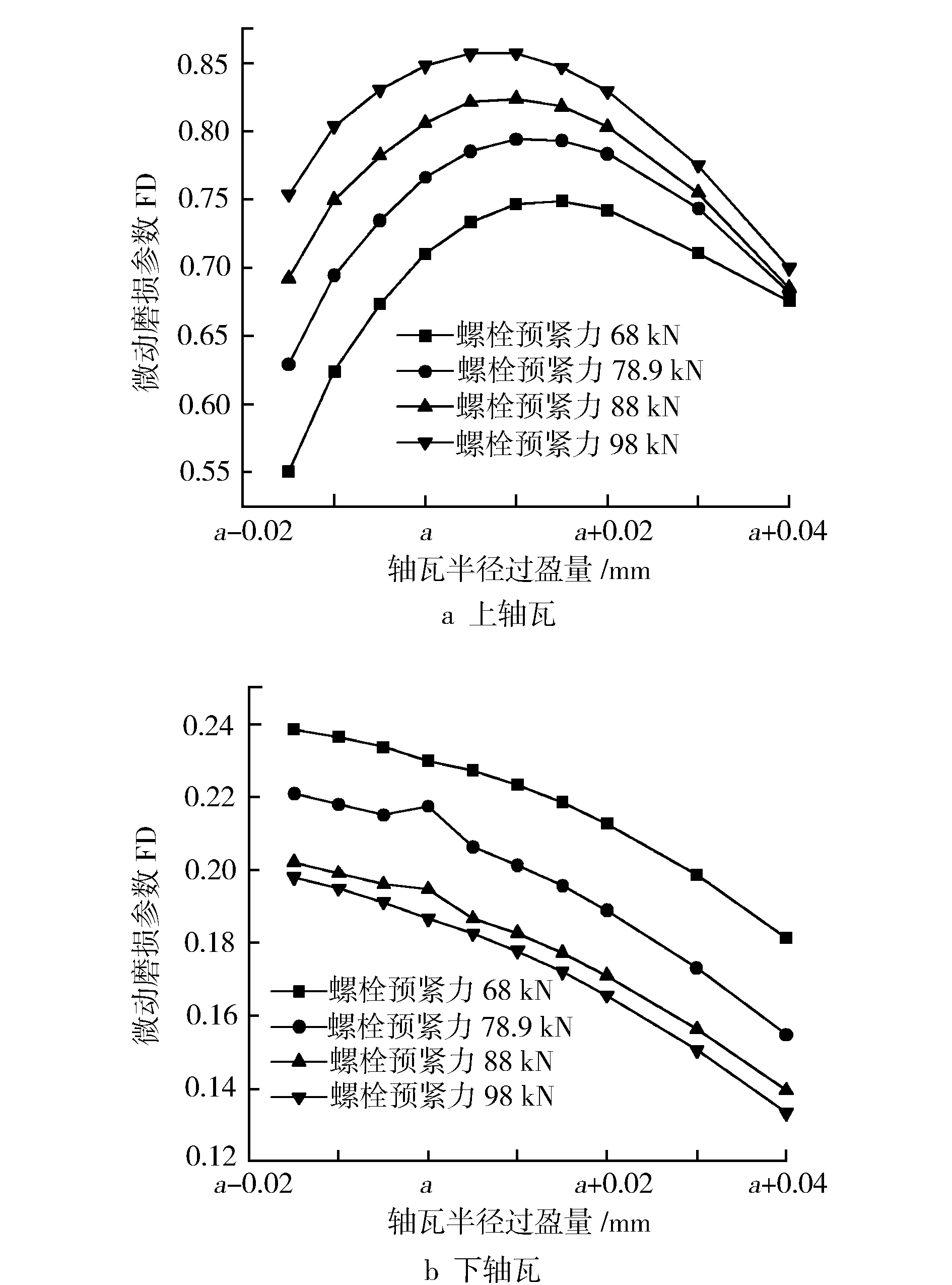
图15 主轴承轴瓦微动磨损与轴瓦过盈量和螺栓预紧力的关系

通过分析轴承应力发现，由于螺栓上端位置与上轴瓦边缘太近，导致上轴瓦边缘应力、应变以及应力应变随循环载荷的变化都很大，从而导致上轴瓦边缘微动磨损较为严重，如图16所示。

因此，想要消除上轴瓦边缘微动磨损大的问题，应该在设计时考虑增大螺栓孔与主轴承之间的距离。

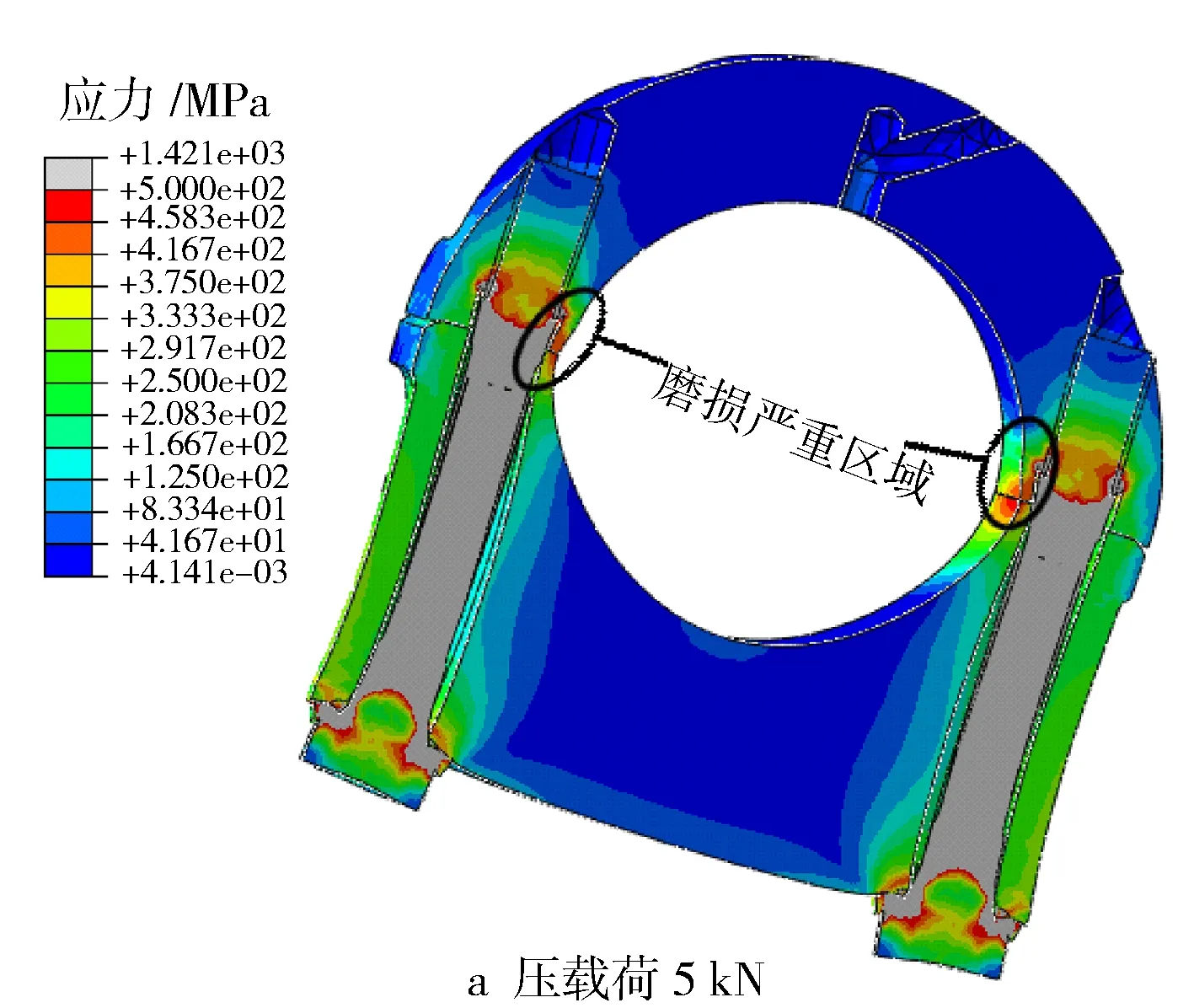
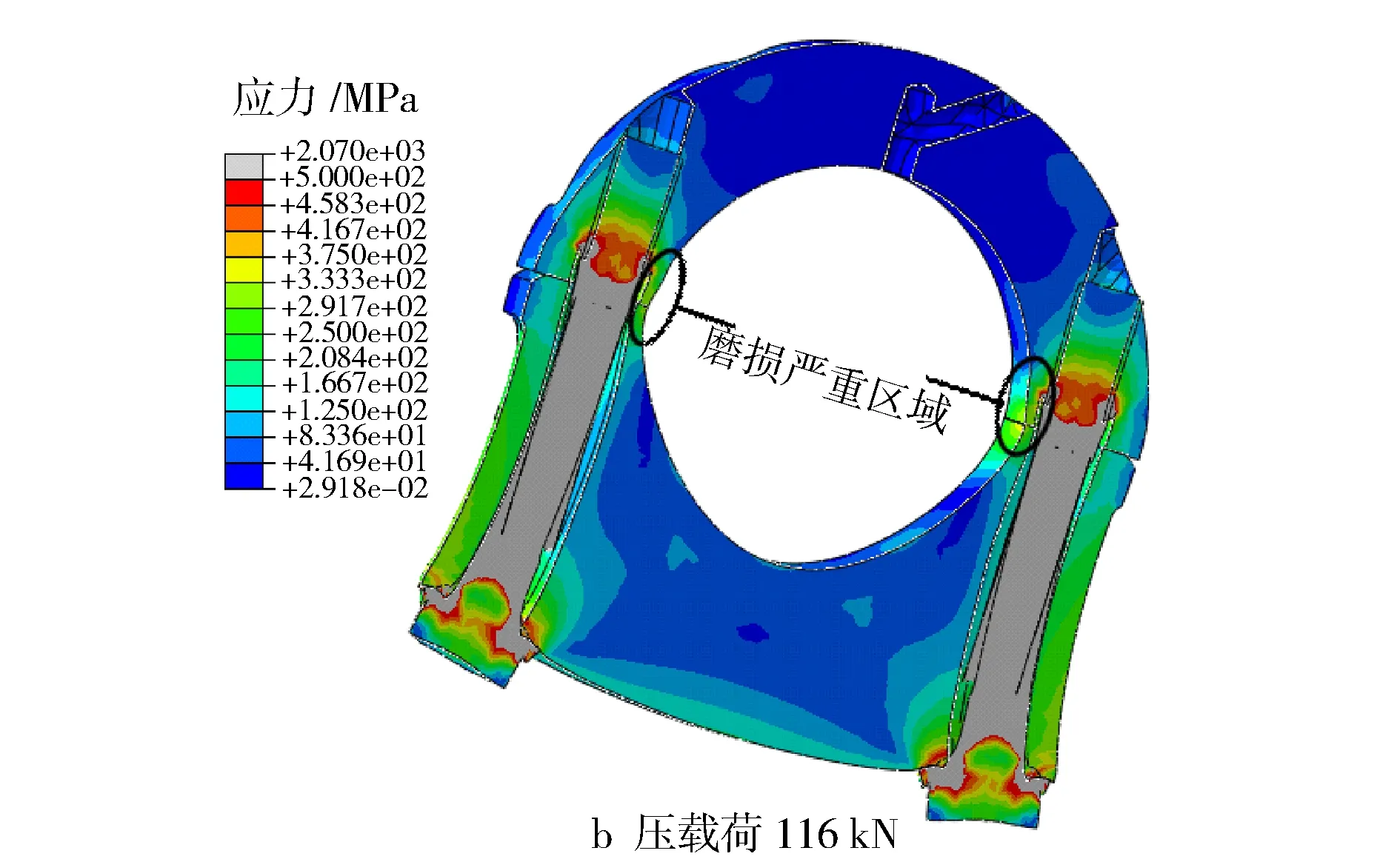
图16 交变载荷下机体-主轴承接触面的应力变化

4 结论

a) 从试验结果看，上瓦磨损严重位置集中在两侧边缘30°区域，下瓦磨损严重位置集中在接触面的中心位置到45°角区域；螺栓预紧力对上下轴瓦磨损影响相反，与上轴瓦正相关，与下轴瓦负相关；

b) 磨损深度仿真结果与试验结果在预紧力对磨损的影响趋势上一致，在磨损分布上也符合很好，验证了该仿真模型的可行性；

c) 通过改变轴瓦过盈量和螺栓预紧力寻找减磨优化方法，得出在当轴瓦半径过盈量大于(a+0.01)mm时，增大轴瓦半径过盈量可以很好地减小上、下瓦背磨损；

d) 分析有限元模型应力发现，由于螺栓上端位置与上轴瓦边缘太近，导致上轴瓦边缘应力、应变以及应力应变随循环载荷的变化都很大，从而导致上轴瓦边缘微动磨损较为严重，因此应该在设计时考虑增大螺栓孔与主轴承之间的距离。